Как найти среднюю скорость при равноускоренном движении

s = v_cp t.

Но, с другой стороны

Сравнивая эти формулы, получим:

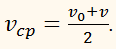
Средняя скорость при равноускоренном движении равна
полусумме начальной и конечной скорости.

Такое простое выражение для средней скорости получается благодаря тому, что
график скорости – это прямая линия, т. е. скорость и время связаны линейной
зависимостью.

Иногда бывает нужно вычислить перемещение тела, движущегося равноускоренно,
когда неизвестно, сколько времени протекло от начала движения, но известны
значения начальной и конечной скорости тела. Формулу, позволяющую вычислить
перемещение, можно получить из формулы

и формулы

v = v₀ + at.

Найдём из последней формулы значение 
t:

и подставим его в формулу

Получаем:

Отсюда

Мы получили, таким образом, формулу, позволяющую вычислить перемещение,
если известны начальная и конечная скорость и ускорение.

Пользуясь формулой

можно также найти значение скорости  v  тела в любой
точке, через которую проходит тело. Из формулы

следует:

или

Откуда

Если начальная скорость тела  v₀  равна нулю, то

ЗАДАЧА:

При подходе к станции машинист
выключил двигатель локомотива, после чего движение происходило с постоянным
ускорением, равным  0,1 м/сек². Какое
перемещение поезд совершил до остановки, если в момент выключения двигателя
скорость поезда была  72 км/час ? Через сколько времени поезд остановился ?

РЕШЕНИЕ:

v₀ = 72 км/час = 20 м/сек,

v = 0  и  a = – 0,1 м/сек²,

• Задание 1
• Задание 2

Другие уроки:

• Урок 1. Движение материальной точки
• Урок 2. Равномерное прямолинейное движение
• Урок 3. График скорости и пути равномерного прямолинейного движения
• Урок 4. Векторные и скалярные величины
• Урок 5. Действия над векторами и их проекциями
• Урок 6. Неравномерное прямолинейное движение
• Урок 7. Ускорение
• Урок 8. Перемещение при прямолинейном равноускоренном движении
• Урок 10. Частные случаи прямолинейного равноускоренного движения
• Урок 11. Криволинейное движение
• Урок 12. Движение по окружности
• Урок 13. Вращение твёрдого тела

Средняя скорость при равноускоренном движении

Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время. Это справедливо и для равноускоренного движения. Модуль средней скорости по перемещению определяется как модуль перемещения, деленный на все время движения. Также перемещение – векторная величина, и имеет направление, следовательно, можно определить и угол, под которым средняя скорость будет направлена к горизонту.

Задача 1.  Тело падает без начальной скорости с высоты м. Найти среднюю скорость падения на второй половине пути.

Чтобы определить среднюю скорость, нужно разделить путь, пройденный телом, на время его движения.

Длина первой половины пути – .

Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:

Полное время падения тоже легко определить:

Тогда определим время, за которое тело прошло вторую половину пути:

Определим среднюю скорость:

Ответ: средняя скорость на второй половине пути равна 25,6 м/c.

Задача 2.  Тело брошено со скоростью м/с вертикально вверх с высоты м над поверхностью земли. Определить среднюю скорость и среднюю путевую скорость за время полета.

Так как найти надо среднюю путевую и среднюю скорость по перемещению, то необходимо знать как путь, так и перемещение тела. Очевидно, что точку старта и точку финиша тела разделяет высота , с которой тело было сброшено, так как в конце оно окажется на земле. Итак, – это перемещение тела.

Чтобы определить путь, потребуется найти высоту, до которой тело смогло подняться. Путь тела тогда будет равен

Максимальная высота подъема тела равна , следовательно,

Также для определения средней скорости надо знать время движения тела. Это время будет складываться из времени взлета и времени падения .

Время взлета найдем из условия равенства нулю скорости тела:

Время падения тоже легко определить, зная, что тело падало с высоты :

Теперь, зная время взлета и время падения, можем определить общее время движения тела:

Осталось разделить путь на это время – и получим среднюю путевую скорость:

Средняя скорость по перемещению равна (или модуль средней скорости):

Задача 3. Мячик брошен с высоты м над поверхностью земли с начальной скоростью м/с под углом к горизонту. Найти модуль и направление его средней скорости за все время полета.

В этой задаче необходимо, по сути, определить вектор средней скорости тела по перемещению: его длину (модуль) и направление. Очевидно, для этого потребуется знать, как далеко тело улетело и сколько на это понадобилось времени.  Мы помним, что проекция скорости тела на горизонтальную ось остается неизменной во времени и равной . Если удастся найти время полета тела – то мы узнаем, как далеко оно шлепнулось о землю.

Давайте запишем закон движения тела по оси :

Так как в итоге ордината тела оказалась равной 0, то приравняем и решим полученное квадратное уравнение:

Один из корней  – отрицательный – отбросим, как неудовлетворяющий смыслу задачи.

Тело улетит от точки старта по горизонтали на расстояние:

Теперь определим перемещение тела по теореме Пифагора:

Разделив перемещение тела на время, получим среднюю скорость по перемещению:

Определим численно, чтобы потом проще было при подсчетах:

Теперь рассчитаем среднюю скрость:

Найдем, под каким углом к горизонту был направлен вектор средней скорости:

Ответ: модуль средней скорости равен 17,3 м/с, она направлена под углом к горизонту.

Часто бывает необходимо знать среднюю скдрость при равноускоренном движении. Как ее вычислить? Мы знаем, что

$s = v_{ср}t$. (1)

Но, с другой стороны, как мы видели (см. § 17),

$s = frac{v_{0} + v }{2}$. (2)

Сравнивая эти формулы, получим:

$v_{ср} = frac{v_{0} + v }{2}$. (3)

Средняя скорость при равноускоренном движении равна полусумме начальной и конечной скорости.

Такое простое выражение для средней скорости получается благодаря тому, что график скорости – это прямая линия, т. е. скорость и время связаны линейной зависимостью.

Иногда бывает нужно вычислить перемещение тела, движущегося равноускоренно, когда неизвестно, сколько времени протекло от начала движения, но известны значения начальной и конечной скорости тела. Формулу, позволяющую вычислить перемещение, можно получить из формулы (2) и формулы

$v = v_{0} + at$. (4)

Найдем из последней формулы значение $t$

$t = frac{v-v_{0} }{a}$

и подставим его в формулу (2). Получаем:

$s = frac{v + v_{0} }{2} frac{v – v_{0} }{a} = frac{(v + v_{0} )(v – v_{0} )}{2a}$.

Отсюда $s = frac{v^{2} – v_{0}^{2} }{2a}$. (5)

Мы получили, таким образом, формулу, позволяющую вычислить перемещение, если известны начальная и конечная скорость и ускорение.

Пользуясь формулой (5), можно также найти значение скорости $v$ тела в любой точке, через которую проходит тело. Из формулы (5) следует:

$v^{2} – v_{0}^{2} = 2as$,

или $v^{2} = v_{0}^{2} + 2as$.

Откуда $| v | = sqrt{v_{0}^{2} + 2as }$, (6)

Если начальная скорость тела $v_{0}$ равна нулю, то

$s = frac{v^{2} }{2a}, |v| = sqrt{2as}$.

Теория равноускоренного движения была разработана знаменитым итальянским ученым Галилео Галилеем. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности.

Приступая к изучению равноускоренного прямолинейного движения, выясним сначала, как находится скорость тела, если известны ускорение этого тела и время движения.

Из формулы (2.1) следует, что при начальной скорости, равной нулю (v₀ = 0),

Эта формула показывает, что для нахождения скорости тела через время t после начала движения надо ускорение тела умножить на время движения.

В противоположном случае, когда тело совершает замедленное движение и в конце концов останавливается (v = 0), формула ускорения (2.2) позволяет найти начальную скорость тела:

Наглядную картину того, как изменяется скорость тела в процессе равноускоренного движения, можно получить, построив график скорости.

Графики скорости впервые были введены в середине XIV в. францисканским ученым-монахом Джиованни ди Казалисом и архидьяконом Руанского собора Никола Оремом, ставшим впоследствии советником французского короля Карла V. По горизонтальной оси они предложили откладывать время, а по вертикальной оси — скорость. В такой системе координат графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро изменяется скорость с течением времени.

Формуле (3.1), описывающей движение с возрастающей скоростью, соответствует, например, график скорости, изображенный на рисунке 5. График, изображенный на рисунке 6, соответствует движению с уменьшающейся скоростью.

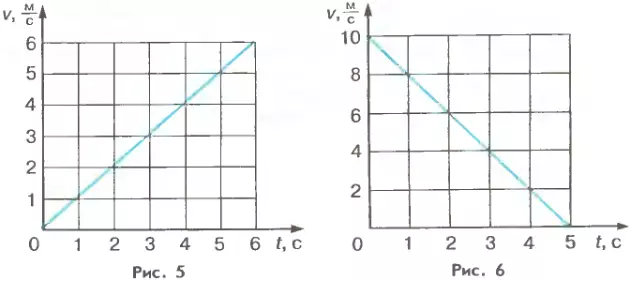
При равноускоренном движении скорость тела непрерывно изменяется. Графики скорости позволяют определить скорость тела в различные моменты времени. Но иногда бывает нужно знать не скорость в тот или иной конкретный момент времени (такую скорость называют мгновенной), а среднюю скорость движения на всем пути.

Задачу о нахождении средней скорости при равноускоренном движении впервые удалось решить Галилею. В своих исследованиях он использовал графический метод описания движения.

Согласно теории Галилея, если скорость тела при равноускоренном движении увеличивается от 0 до некоторого значения v, то средняя скорость движения будет равна половине достигнутой скорости:

Аналогичная формула справедлива и для движения с уменьшающейся скоростью. Если она уменьшается от некоторого начального значения v0 до 0, то средняя скорость такого движения оказывается равной

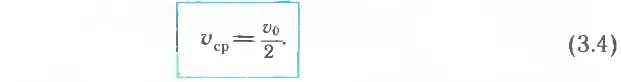
Полученные результаты можно проиллюстрировать с помощью графика скорости. Так, например, для нахождения средней скорости движения, которому соответствует график на рисунке 5, мы должны найти половину от 6 м/с. В результате получаем 3 м/с. Это и есть средняя скорость рассматриваемого движения.

1. Кто является автором первой теории равноускоренного движения? 2. Как находится скорость тела при равноускоренном движении из состояния покоя? 3. Используя график, изображенный на рисунке 5, определите скорость тела через 2 с после начала движения. 4. Используя график, изображенный на рисунке 6, определите среднюю скорость движения тела.