Как найти среднюю скорость пути математика - Сайт, где вы сможете решить свои вопросы

Здравствуйте, дорогие читатели, подписчики и гости канала. Рассмотрим задачи на среднюю скорость.

Задачи на среднюю скорость достаточно простые, но многие допускают ошибку в ее вычислении.

Средняя скорость рассчитывается для неравномерного движения. Средняя скорость – это отношение всего пути на время в течении которого этот путь был пройден.

Рассмотрим в чем различие нахождение скорости движения с постоянной скоростью на всем пути от нахождения скорости при неравномерном движении на всем пути.

Задачи на среднюю скорость. Задание №21 ОГЭ

Рассмотрим решение нескольких задач.

Задача №1

Чтобы найти среднюю скорость, нам нужно найти время на каждом участке пути. В нашей задаче таких участков три.

Зная время на каждом участке пути, можем найти среднюю скорость:

Задача №2

В этой задаче у нас два участка пути. За весь пусть возьмем S. Тогда половина пути равна S/2

Теперь воспользуемся формулой, и найдем среднюю скорость на протяжении всего пути:

В задачах может встречаться и задачи, где пройдено путь необязательно делится пополам, но и в других отношениях: например 2/3 пути и 1/3 пути. Но смыл решения задач одинаков.

Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.

Путеводитель по каналу здесь

Источник

Задачи ЕГЭ на нахождение средней скорости

На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:

$v_{cp}=genfrac{}{}{}{0}{displaystyle S_o}{displaystyle t_o}$ ,

где $v_{cp}$ — средняя скорость, S_o – общий путь, t_o — общее время.

Если участков пути было два, то
$v_{cp}=genfrac{}{}{}{0}{displaystyle S_1 + S_2}{displaystyle t_1+t_2}$

Путешественник переплыл море на яхте со средней скоростью км/ч. Обратно он летел на спортивном самолете со скоростью км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем только, что это расстояние было одинаковым на пути туда и обратно. Для простоты примем это расстояние за (одно море). Тогда время, которое путешественник плыл на яхте, равно $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}$ , а время, затраченное на полет, равно $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 480}$ . Общее время равно $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}+genfrac{}{}{}{0}{displaystyle 1}{displaystyle 480}=genfrac{}{}{}{0}{displaystyle 25}{displaystyle 480}=genfrac{}{}{}{0}{displaystyle 5}{displaystyle 96}$ .

Средняя скорость равна 38,4 км/ч.

Ответ: 38,4 .

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Средняя скорость – это вовсе не среднее арифметическое скоростей. По определению,

Найдем S_1 , S_2 и S_3 по формуле: S_ =vt.

Получим, что км, км, км,

км.

Ответ: 70.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на нахождение средней скорости» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Запомните!

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму
на их количество.

Пример:

Найти среднее арифметическое 2, 3 и 4.

Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.

2 + 3 + 4 = 9

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Средняя цена = =
= 320 руб.

Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.

Запомните!

Средняя скорость движения — это весь пройденный путь разделить на всё время движения.

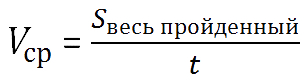
Рассмотрим задачу на среднюю скорость.

Разбор примера

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.

S₁ = V₁t₁

S₁ = 90 · 3,2 = 288 (км)

— шоссе.

S₂ = V₂t₂

S₂ = 45 · 1,5 = 67,5 (км)

— грунтовая дорога.

S₃ = V₃t₃

S₃ = 30 · 0,3 = 9 (км)

— просёлочная дорога.

S = S₁ + S₂ + S₃

S = 288 + 67,5 + 9 = 364,5 (км)

— весь путь, пройденный автомобилем.

t = t₁ + t₂ + t₃

t = 3,2 + 1,5 + 0,3 = 5 (ч)

— всё время.

V_ср = S : t

V_ср = 364,5 : 5 = 72,9

(км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

10 апреля 2015 в 18:52

Дарья Некрасова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Дарья Некрасова
Профиль
Благодарили: 0

Сообщений: 3

Автомобиль проехал 180 км за 3 ч с одинаковой скоростью. Из-за гололёда на обратном пути он уменьшил скорость на 15 км/ч. Сколько времени затратил автомобиль на обратный путь.

0
Спасибо thanks
Ответить

10 апреля 2015 в 18:55
Ответ для Дарья Некрасова

Дарья Некрасова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Дарья Некрасова
Профиль
Благодарили: 0

Сообщений: 3

180: 3=60
60 ?15=45
180 :45=4

0
Спасибо thanks
Ответить

14 апреля 2015 в 17:11
Ответ для Дарья Некрасова

Asel Talantbekovna
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Asel Talantbekovna
Профиль
Благодарили: 0

Сообщений: 8

сама себе отвечает?

0
Спасибо thanks
Ответить

Источник

24
Фев 2013

Категория: 09 Текстовые задачиСправочные материалыТекстовые задачи

09. Текстовые задачи на среднюю скорость

2013-02-24
2022-09-11

Средняя скорость – есть отношение всего пройденного пути ко всему затраченному времени.

Задача 1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью км/ч, а вторую половину времени – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Задача 2. Первые два часа автомобиль ехал со скоростью км/ч, следующий час – со скоростью км/ч, а затем два часа – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Задача 3. Первую треть трассы автомобиль ехал со скоростью км/ч, вторую треть – со скоростью км/ч, а последнюю – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение: + показать

Задача 4. Путешественник переплыл море на яхте со средней скоростью км/ч. Обратно он летел на спортивном самолете со скоростью км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ ч.

Решение: + показать

Вы можете пройти тест по теме «Задачи на среднюю скорость»

Автор: egeMax |

комментариев 11
| Метки: тесты

Источник

Средняя скорость

Главная
/
Физика
/
Средняя скорость

Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Средняя скорость на протяжении всего пути

Расстояние (путь)

S =

Время

t =

Средняя скорость

V_ср =

Округление ответа:

Средняя скорость через несколько скоростей

Средняя скорость

V_ср =

Округление ответа:

Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.

Теория

Как найти среднюю скорость зная расстояние (путь) и время

Чему равна средняя скорость V_ср если известны путь S и время t за которое этот путь преодолён?

Формула

V_ср = ^S⁄_t

Пример

К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:

V_ср = 1000/16 = 62.5 км/ч

Как найти среднюю скорость зная скорости на участках пути

Чтобы найти среднюю скорость V_ср на протяжении всего пути, зная показатели скорости на его участках (V₁ , V₂ , … V_n), следует найти среднее гармоническое этих скоростей.

Формула

V_ср	=	n
¹⁄_V₁ + ¹⁄_V₂ + … + ¹⁄_{V_n}

Пример

Средняя скорость через две скорости

Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:

V_ср	=	2	=	2	= 32
¹⁄₈₀ + ¹⁄₂₀	0.0125 + 0.05

Средняя скорость автомобиля равна 32 км/ч.

Источник

Задачи ЕГЭ на нахождение средней скорости

Для чего нужно среднее арифметическое?

Средняя скорость движения

Разбор примера

Ваши комментарии

09. Текстовые задачи на среднюю скорость

Средняя скорость

Онлайн калькулятор

Средняя скорость на протяжении всего пути

Средняя скорость через несколько скоростей

Теория

Как найти среднюю скорость зная расстояние (путь) и время

Формула

Пример

Как найти среднюю скорость зная скорости на участках пути

Формула

Пример

Средняя скорость через две скорости

Вам также может понравиться

Как составить самой конкурс

Как найти работу в государственной думе рф

Как найти средний бал в школе

Добавить комментарий Отменить ответ