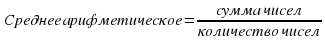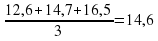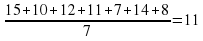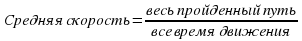Версия для печати и копирования в MS Word
1
Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую — со скоростью 96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
2
Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
3
Первую половину пути автомобиль проехал со скоростью 34 км/ч, а вторую — со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
4
Первую половину пути автомобиль проехал со скоростью 90 км/ч, а вторую — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
5
Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую со скоростью 108 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
6
Первую половину трассы автомобиль проехал со скоростью 60 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
7
Первую половину пути автомобиль проехал со скоростью 36 км/ч, а вторую со скоростью 99 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
8
Первую половину трассы автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 72 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
9
Первую половину пути автомобиль проехал со скоростью 90 км/ч, а вторую со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
10
Первую половину трассы автомобиль проехал со скоростью 39 км/ч, а вторую — со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
11
Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
12
Первую половину трассы автомобиль проехал со скоростью 30 км/ч, а вторую — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
13
Первую половину пути автомобиль проехал со скоростью 69 км/ч, а вторую со скоростью 111 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
14
Первую половину трассы автомобиль проехал со скоростью 52 км/ч, а вторую — со скоростью 78 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
15
Первую половину пути автомобиль проехал со скоростью 60 км/ч, а вторую со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
16
Первую половину трассы автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 108 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
17
Первую половину трассы автомобиль проехал со скоростью 45 км/ч, а вторую — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
18
Первую половину пути автомобиль проехал со скоростью 34 км/ч, а вторую со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
19
Первую половину трассы автомобиль проехал со скоростью 40 км/ч, а вторую — со скоростью 85 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
20
Первую половину пути автомобиль проехал со скоростью 54 км/ч, а вторую со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
21
Первую половину трассы автомобиль проехал со скоростью 78 км/ч, а вторую — со скоростью 91 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22
Первую половину трассы автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 102 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
23
Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую со скоростью 108 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
24
Первую половину пути автомобиль проехал со скоростью 36 км/ч, а вторую со скоростью 99 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
25
Первую половину пути автомобиль проехал со скоростью 90 км/ч, а вторую со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
26
Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
27
Первую половину пути автомобиль проехал со скоростью 69 км/ч, а вторую со скоростью 111 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
28
Первую половину пути автомобиль проехал со скоростью 60 км/ч, а вторую со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
29
Первую половину пути автомобиль проехал со скоростью 34 км/ч, а вторую со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
30
Первую половину пути автомобиль проехал со скоростью 54 км/ч, а вторую со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
31
Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую со скоростью 96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
В открытом банке заданий ФИПИ есть задачи на нахождение средней скорости движения автомобиля. В этих задачах ученики допускают больше всего ошибок.
Типичные ошибки в задачах:
– ! Находят среднюю скорость движения как среднее арифметическое двух скоростей ( Vср. = 𝑉1+𝑉2 / 2 );
– Решают задачу на среднюю скорость, рассматривая только частные случаи (придают величине пути всевозможные значения -1 км., или 108 км.);
– Приписывают единицы измерения, не соответствующие данным величинам;
– Забывают записывать единицы измерения к введенным значениям;
– Допускают записи вида: составим уравнение, а сами составляют выражения и их преобразования, неоднократно используют при этом знак равенства;
– Не вводят переменные величины, а используют при составлении уравнений;
– Не показано как составлено уравнение (формула)
– Путают понятия скорости и времени движения;
– Допускают вычислительные ошибки;
– Записывают ответ, используя приближения (≈);
– Используют формулу для нахождения средней скорости без ее вывода;
– Отсутствие краткой записи к решению задачи, и таблицы, и обоснований, решение задачи выглядит как столбик примеров без каких бы то ни было пояснений;
– Использование неравносильных преобразований при решении уравнений.
Как решать и оформлять задания на нахождение средней скорости
Решение должно быть полностью логически обосновано с начала до конца.
Если задача решается через х – пишите, что принимаете за х, какие еще будут составляющие с неизвестными.
Если решаете через формулу средней скорости, обязательно сначала нужно ее вывести следующим образом.

Пример. Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение через формулу пути
Дано:
v1= 42 км/ч
v2= 48 км/ч
S1=S2
vср – ?Решение:
S1=S/2 км, v1=42 км/ч, значит $t_1=frac{displaystylefrac S2}{42}=frac S{84}$
S2=S/2 км, v2=48 км/ч, значит $t_2=frac{displaystylefrac S2}{48}=frac S{96}$
Найдем среднюю скорость на протяжении всего пути
$v_{ср}=frac{S_1+S_2}{t_1+t_2}$
$v_{ср}=frac{{displaystylefrac S2}+{displaystylefrac S2}}{{displaystylefrac S{84}}+{displaystylefrac S{96}}}=frac S{displaystylefrac{84S+96S}{84ast96}}=frac{cancel S}{displaystylefrac{180cancel S}{84ast96}}=frac{84ast96}{180}=44,8$ км/ч
Ответ: 44,8 км/ч.
В задаче может быть не 2 половины пути, а, допустим, 1/3 и 2/3 пути, или еще больше разных частей. Выразив S1, S2 и тд. , умножив S на соответствующую часть, сможем решить и такие задачи.
Та же задача. Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение через формулу определения средней скорости
Дано:
v1= 42 км/ч
v2= 48 км/ч
S1=S2
vср – ?Решение:
vср=S/t, где t=t1+t2
t1 – время, затраченное на первую половину пути, t2 – время, затраченное на первую половину пути.
$t_1=frac{displaystylefrac S2}{v_1}$
$t_2=frac{displaystylefrac S2}{v_2}$Подставляем в исходную формулу средней скорости:
$v_{ср}=frac S{{displaystylefrac{{displaystylefrac12}S}{v_1}}+{displaystylefrac{{displaystylefrac12}S}{v_2}}}=frac S{{displaystylefrac12}S({displaystylefrac1{v_1}}+{displaystylefrac1{v_2}})}=frac2{{displaystylefrac1{v_1}}+{displaystylefrac1{v_2}}}=frac{2v_1v_2}{v_1+v_2}$
$v_{ср}=frac{2ast42ast48}{42+48}=frac{2ast42astcancel{48}^{8}}{cancel{90}^{15}}=frac{2astcancel{42}^{14}ast8}{cancel{15}^{5}}=frac{224}5=44,8$ км/ч
Ответ: 44,8 км/ч.
Можно так же сразу вместо v1 и v2 подставлять известные скорости и преобразовывать уже с числами, а не с буквами.
Другой вариант оформления задач такого типа (с таблицей)
Первую половину пути автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 99 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Пусть х км – половина пути.
S км v км/ч t ч
1 х 36 х/36
2 х 99 х/99$v_{ср}=frac{S_{общ.}}{t_{общ.}}=frac{х;+;х}{{displaystylefrac{х^{(99}}{36}}+{displaystylefrac{х^{(36}}{99}}}=frac{2х}{displaystylefrac{99х;+;36х}{36ast99}}=2х:frac{135х}{36ast99}=frac{2cancel хastcancel{36}^{12}astcancel{99}^{11}}{;{}_{5;cancel{15}}cancel{135}cancel х}=frac{2ast132}5=frac{264}5=52,8$ км/ч
Значит, средняя скорость равна 52,8 км/ч
Ответ: 52,8 км/ч.
И еще один вариант оформления той же задачи.
Пусть 2S км – весь путь. Тогда время, затраченное на первую половину пути t1=S/36 ч; на вторую половину пути t2=S/99 ч.
$v_{ср}=frac{S_{общ.}}{t_{общ.}}=frac{S_{общ.}}{t_1+t_2}=frac{2S}{{displaystylefrac S{displaystyleunderset{4ast9}{36}}}+{displaystylefrac S{displaystyleunderset{11ast9}{99}}}}=frac{2S}{displaystylefrac{15S}{4ast9ast11}}=frac{4astcancel9^3ast11ast2cancel S}{{}_{5;}cancel{15}cancel S}=frac{264}5=52,8$ км/ч
Ответ: 52,8 км/ч.
Рассмотрим задачу другого типа.
Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км — со скоростью 60 км/ч, а последние 500 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Чтобы найти среднюю скорость, нужно найти время на каждом участке пути. В нашей задаче таких участков 3.
S1=105 км ; v1=35 км/ч; значит t1=105/35=3 часа
S2=120 км ; v2=60 км/ч; значит t2=120/60=2 часа
S3=500 км ; v3=100 км/ч; значит t3=500/100=5 часов
Зная время на каждом участке пути, найдем среднюю скорость:
$v_{ср.}=frac{S_1+S_2+S_3}{t_1+t_2+t_3}=frac{105+120+500}{3+2+5}=frac{725}{10}=72,5$ км/ч
Ответ: 72,5 км/ч.
Если вы специалист по подготовке к ОГЭ, напишите, пожалуйста, в комментариях, какой вариант оформления, по вашему мнению, наиболее предпочтителен.
Если вы сдали ОГЭ и за задачу у вас 2 балла, поделитесь, как оформляли, писали Дано и Решение?
|
Среднее арифметическое |
|
|
Среднее арифметическое нескольких чисел — это отношение суммы всех чисел к их количеству. |
|
ПРИМЕРЫ:
|
Найти среднее арифметическое чисел: 12,6, 14,7 и 16,5. |
Ответ. 14,6 |
|
На курсы английского языка в понедельник пришло 15 человек, во вторник — 10, в среду — 12, в четверг — 11, в пятницу — 7, в субботу — 14, в воскресенье — 8. Найти среднюю посещаемость курсов за неделю. |
Ответ. 11 |
|
Средняя скорость |
|
|
Средняя скорость — это отношение всего пройденного пути ко всему затраченному времени. |
|
|
Половина всего времени |
|
|
Половина всего пути |
|
Задача 1. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение.
|
V |
t |
S |
|
|
I |
50 км/ч |
2 ч |
50 2 = 100 км |
|
II |
100 км/ч |
1 ч |
100 1 = 10 км |
|
III |
75 км/ч |
2 ч |
75 2 = 150 км |
|
ВСЕГО |
5 ч |
260 км |
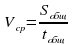
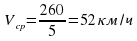
Ответ. 52 км/ч
Задача 2. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение.
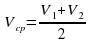
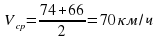
Ответ. 70 км/ч
Задача 3. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение.
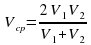
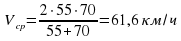
Ответ. 61,6 км/ч
Средняя скорость равна отношению пройденного расстояния к затраченному времени.
Значит, нужно:
- найти пройденный путь;
- найти время, которое автомобиль находился в пути;
- разделить найденный путь на это время.
Для удобства расчётов внесём данные о расстоянии и скорости в таблицу и найдем время:
|
(displaystyle S) |
(displaystyle v) скорость, км/ч |
(displaystyle t=frac {S}{v}) время, ч |
|
| 1 | (displaystyle 190) | (displaystyle 50) | (displaystyle frac{190}{ 50 }=frac{19}{ 5}) |
| 2 | (displaystyle 180) | (displaystyle 90) | (displaystyle frac{180}{ 90 }=2) |
| 3 | (displaystyle 170) | (displaystyle 100) | (displaystyle frac{170}{100 }=frac{17}{10}) |
| Итого | (displaystyle 190+180+170= red{540}) | – | (displaystyle frac{19}{ 5}+2+frac{17}{10}) |
Найдем общее время в пути:
(displaystyle frac{19}{ 5}+2+frac{17}{10}=frac{38}{10}+frac{20}{10}+frac{17}{10}=frac{38+20+17}{10}=frac{75}{10}=blue{frac{15}{2}}) ч.
Значит, в сумме автомобиль проехал (displaystyle red{540}) км и потратил на весь путь (displaystyle blue{frac{15}{2}}) часа.
Найдём среднюю скорость:
(displaystyle v_{text ср}=frac{ phantom{1}red{540}phantom{1}}{ blue{dfrac{15}{2}}}=540:frac{ 15}{ 2 }=540cdot frac{ 2}{ 15 }=72) км/ч.
Ответ: (displaystyle 72)