Как найти среднюю ставку в процентах

Как определить среднюю процентную ставку

В процессе анализа финансово-хозяйственной деятельности предприятий иногда требуется определить стоимость заемного капитала, уровень доходности по депозитам или ценным бумагам. Для этого применяются средние процентные ставки.

Инструкция

Чтобы узнать стоимость обслуживания кредитного портфеля, рассчитайте средневзвешенную процентную ставку по всем привлеченным кредитам. Вычислите общую сумму расходов на уплату процентов за год, умножив размер кредита на процентную ставку по каждому договору в отдельности и сложив полученные величины. Разделите итоговое значение на показатель кредитной массы предприятия и умножьте частное на 100.

Для расчета средневзвешенных ставок по кредитам и депозитам используйте формулу, предложенную Центральным Банком РФ:
Pav = (V1 x P1 + V2 x P2 + … + Vn x Pn):(V1 + V2 + … + Vn), где
V1, V2, …, Vn – объем кредитов или депозитов,
Р1, Р2, …, Рn – номинальная процентная ставка по договору.

При кредитовании в разных банках и наличии большого количества договоров для удобства производите расчеты с помощью электронной таблицы: в столбце А укажите сумму кредита, в столбце В – процентную ставку, в столбце С задайте формулу расчета суммы годовых процентов (А х В), а в нижней части таблицы – формулу вычисления итогов по столбцам. В отдельной ячейке установите алгоритм расчета средневзвешенной ставки:
(Итог столбца С / Итог столбца А) х 100.

Если вам не известны процентные ставки в разрезе договоров, но имеется общая сумма расходов на уплату процентов по кредитам, разделите ее на общий объем кредитной массы и умножьте на 100 – вы получите средневзвешенную ставку.

Кроме того, кредитные и депозитные сделки могут оформляться на условиях переменной процентной ставки. В таком случае ее среднее значение нужно рассчитывать с учетом изменения ее величины в течение всего периода действия договора. Для этого умножьте сумму кредита на процентную ставку, разделите на количество дней в году (365 или 366) и умножьте на число дней, когда она применялась. Рассчитайте и сложите значения процентных расходов для каждой ставки, затем разделите общую сумму на размер кредита и умножьте полученный результат на 100.

Источники:

• средневзвешенная процентная ставка это

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Проблема
эквивалентности ставок в некоторых
случаях может быть решена и с помощью
расчета средних значений ставок. Если
речь идет об одной финансовой операции,
в которой размер ставки изменяется во
времени, то все значения ставки можно
обобщить с помощью соответствующей
средней. Причем замена всех усредняемых
значений ставки на среднюю ставку не
должна изменить результаты наращения
или дисконтирования.

Искомые
средние получим при приравнивании
множителей наращения друг к другу.
Начнем с простой ставки. Пусть за периоды
n₁,
n₂,…,
n_k
начисляются
простые проценты по ставкам
i₁,
i₂,…,
i_k,
тогда на основе равенства множителей
наращения:

;

где
N =

—
общий срок наращения;

— средняя
ставка;

получим искомую
среднюю:

Найденная
характеристика представляет собой
арифметическую среднюю взвешенную с
весами, равными продолжительности
отдельных периодов.

Аналогичным
способом получим среднюю учетную ставку:

Пример
3.17. Контракт
предусматривает переменную по периодам
ставку простых процентов: 20; 22 и 25%.
Продолжительность периодов: два, три и
пять месяцев. Какой размер ставки
приведет к аналогичному наращению
исходной суммы? Находим среднюю:

Если усредняются
переменные во времени ставки сложных
процентов, то из равенства множителей
наращения

следует:

(3.36)

Средняя в этом
случае, как видим, вычисляется как
взвешенная средняя геометрическая.

Пример
3.18. Допустим,
для первых двух лет ссуды применяется
ставка, равная 15%, для следующих трех
лет она составляет 20%. Средняя ставка
за весь срок ссуды равна

или
17,974%.

Рассмотрим
теперь усреднение ставок, применяемых
в нескольких однородных операциях,
которые различаются суммой долга P_t
и ставкой
процента i_t.
Искомые
средние ставки находим из условия
равенства соответствующих сумм после
наращения процентов. Так, если применяются
простые ставки и сроки этих операций
одинаковы, то можно записать следующее
исходное равенство:

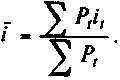
(3.37)

Как видим, искомая
ставка равна взвешенной арифметической
средней; в качестве весов берутся размеры
ссуд.

Усреднение сложных
ставок для тех же условий достигается
с помощью взвешенной степенной средней:

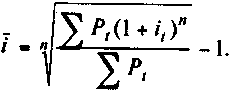
(3.38)

Пример
3.19. Выданы
две ссуды: Р₁
= 1 млн. руб.,
P₂
= 2 млн. руб. Первая выдана под 20% годовых,
вторая — под 30%, сроки ссуд одинаковы и
равны полутора годам. Если ставки
простые, то:

=
0,2667.

Для сложных ставок
находим:

=
0,2671.

Формулы (3.37) и
(3.38) получены для частного случая, когда
сроки ссуд одинаковы. В более общих
случаях они, разумеется, не работают.
Решение соответствующих задач возможно
на основе методов, разработанных для
так называемых потоков платежей. Эти
методы обсуждаются в следующем разделе
книги.

Раздел 2 Потоки платежей Глава 4. Постоянные финансовые ренты

4.1. Виды потоков платежей и их основные параметры

Современные
финансово-банковские операции часто
предполагают не отдельные или разовые
платежи, а некоторую их последовательность
во времени. Например, погашение
задолженности в рассрочку, периодическое
поступление доходов от инвестиций,
выплата пенсий и т. д. Такие последовательности,
или ряды, платежей назовем потоком
платежей. Заметим, что
в западной финансовой литературе в
аналогичном смысле применяется термин
“cash
flows”
(буквально — потоки наличности). Отдельный
элемент этого ряда назовем членом
потока. Введение
понятия “поток платежей” в практику
финансового количественного анализа,
что произошло сравнительно недавно,
заметно расширило рамки и возможности
последнего.

Классификация
потоков. Потоки
платежей могут быть регулярными и
нерегулярными. В нерегулярном потоке
платежей членами являются как положительные
(поступления), так и отрицательные
величины (выплаты), а соответствующие
платежи могут производиться через
разные интервалы времени.

Поток
платежей, все члены которого положительные
величины, а временные интервалы между
платежами одинаковы, называют финансовой
рентой, или
просто рентой,
а иногда
аннуитетом
(annuity)
независимо от назначения или происхождения
платежей. Например, рентой являются
последовательность получения процентов
по облигации, платежи по потребительскому
кредиту, выплаты в рассрочку страховых
премий и т. д. Как видим, во всех приведенных
случаях выплаты или получения денег
производятся через равные промежутки
времени. Использование в финансово-банковской
операции условий, предполагающих выплаты
в виде финансовой ренты, существенно
упрощает количественный их анализ, дает
возможность применять стандартные
формулы и таблицы значений ряда
необходимых для расчетов коэффициентов
и быстро выполнять расчеты на калькуляторах.

Рента
характеризуется следующими параметрами:
член ренты
(rent)
— размер отдельного платежа, период
ренты (rent
period,
payment
period)
— временной интервал между двумя
последовательными платежами, срок
ренты (term)
— время от начала первого периода ренты
до конца последнего периода, процентная
ставка. Размер
ставки не всегда прямо оговаривается
в условиях финансовой ренты, вместе с
тем этот параметр крайне необходим для
ее анализа.

При характеристике
отдельных видов рент необходимы
дополнительные условия и параметры:
число платежей в году, способ и частота
начислений процентов.

В практике применяют
разные по своим условиям ренты. В основу
их классификации могут быть положены
различные признаки. Рассмотрим некоторые
из таких классификаций.

По
количеству выплат членов ренты на
протяжении года ренты делятся на годовые
(выплата раз
в году) и р-срочные
(р — количество
выплат в году). В анализе производственных
инвестиционных процессов иногда
применяют ренты с периодами, превышающими
год. Перечисленные виды рент называют
дискретными.
В финансовой
практике встречаются и с такими
последовательностями платежей, которые
производятся столь часто, что их
практически можно рассматривать как
непрерывные.

По
количеству начислений процентов на
протяжении года различают: ренты с
ежегодным начислением, с начислением
т раз
в году, с непрерывным начислением.
Моменты начисления процентов необязательно
совпадают с моментами выплат членов
ренты. Однако, как будет показано, расчеты
заметно упрощаются, если два указанных
момента совпадают.

По
величине своих членов ренты делятся на
постоянные
(с одинаковыми
платежами) и переменные.
Члены
переменных рент изменяют свои размеры
во времени, следуя какому-либо закону,
например арифметической или геометрической
прогрессии, либо несистематично (задаются
таблицей).

По
вероятности выплат ренты делятся на
верные
(annuity
certain)
и условные
(contingent
annuity).
Верные ренты подлежат безусловной
уплате, например при погашении кредита.
Число членов такой ренты заранее
известно. В свою очередь выплата условной
ренты ставится в зависимость от
наступления некоторого случайного
события. Поэтому число ее членов заранее
неизвестно. К такого рода рентам относятся
страховые
аннуитеты — различные
последовательные платежи в имущественном
и личном страховании. Типичным примером
страхового аннуитета является пожизненная
выплата пенсии.

По
количеству членов различают ренты с
конечным числом членов, т. е. ограниченные
по срокам ренты
(их срок заранее оговорен), и бесконечные,
или вечные,
ренты
(perpetuity).
С вечной рентой встречаются на практике
в ряде долгосрочных операций, когда
предполагается, что период функционирования
анализируемой системы или срок операции
весьма продолжителен и не оговаривается
конкретными датами. В качестве вечной
ренты логично рассматривать и выплаты
процентов по облигационным займам с
неограниченными сроками.

По
соотношению начала срока ренты и
какого-либо момента времени, упреждающего
начало ренты (например, начало действия
контракта или дата его заключения),
ренты делятся на немедленные
и отложенные,
или отсроченные
(deffered
annuity).

Очень
важным является различие рент по моменту
выплат платежей в пределах периода.
Если платежи осуществляются в конце
периодов, то соответствующие ренты
называют обыкновенными,
или постнумерандо (ordinary
annuity),
если же платежи производятся в начале
периодов, то их называют пренумерандо
(annuity
due).
Иногда контракты предусматривают
платежи или поступления денег в середине
периодов.

Приведем пример.
Контракт предусматривает периодическое
погашение задолженности выплатой в
конце каждого полугодия одинаковых
погасительных платежей на протяжении
фиксированного числа лет. Таким образом,
предусматривается постоянная, полугодовая,
верная, ограниченная рента постнумерандо.
Если первая выплата в счет погашения
основной суммы долга производится
спустя, скажем, два года после подписания
контракта (льготный период), то эта рента
является отложенной относительно даты
заключения договора.

Обобщающие
параметры потоков платежей. В подавляющем
числе практических случаев анализ
потока платежей предполагает расчет
одной из двух обобщающих характеристик:
наращенной суммы или современной
стоимости. Наращенная
сумма (amount
of
cash
flows)
— сумма всех членов потока платежей с
начисленными на них к концу срока
процентами. Под современной
стоимостью потока платежей (present
value
of
cash
flows)
понимают сумму всех его членов,
дисконтированных на начало срока ренты
или некоторый упреждающий момент
времени. (В старой русской финансовой
литературе аналогичный по содержанию
показатель назывался настоящей
ценой платежей.)
Конкретный смысл этих характеристик
определяется содержанием его членов
или их происхождением. Наращенная сумма
может представлять собой общую сумму
накопленной задолженности к концу
срока, итоговый объем инвестиций,
накопленный денежный резерв и т. д. В
свою очередь современная стоимость
характеризует приведенные к началу
осуществления проекта инвестиционные
затраты, суммарный капитализированный
доход или чистую приведенную прибыль
от реализации проекта и т. п.

Обобщающие поток
платежей характеристики, особенно его
современная стоимость, широко применяются
в различных финансовых расчетах. Так,
без них, например, невозможно разработать
план последовательного погашения
задолженности, измерить финансовую
эффективность проекта, осуществить
сравнение или безубыточное изменение
условий контрактов, решить многие другие
практические задачи. В связи со сказанным
основное внимание в данной главе уделено
методам расчета наращенных сумм и
современных стоимостей постоянных
финансовых рент. Однако до этого
необходимо обсудить более общие подходы,
применяемые при определении названных
параметров при анализе нерегулярных
потоков платежей.

Прямой
метод расчета наращенной суммы и
современной стоимости потока платежей.
Рассмотрим
общую постановку задачи. Допустим,
имеется ряд платежей R_t,
выплачиваемых
спустя время п_t
после
некоторого начального момента времени,
общий срок выплат я лет. Необходимо
определить наращенную на конец срока
сумму потока платежей. Если проценты
начисляются раз в году по сложной ставке
i,
то, обозначив искомую величину через
S,
получим по
определению:

(4.1)

Как
видим, наращенную сумму в заданных
условиях получают методом прямого
счета. Современную стоимость такого
потока находим прямым счетом — как
сумму дисконтированных платежей.
Обозначив эту величину как А,
получим:

(4.2)

где
—

дисконтный множитель по ставке i.

Современная
стоимость потока платежей представляет
собой его обобщающую
оценку, приуроченную к некоторому
предшествующему моменту времени (у
немедленной ренты — к началу срока).
Наращенная сумма — это тоже не что иное,
как представление всех членов потока
в виде одного числа, однако приурочена
эта оценка к концу срока. Нетрудно
обнаружить, что между величинами А
и S
существует
функциональная зависимость. В самом
деле, дисконтировав сумму S
с
помощью
дисконтного множителя vⁿ,
получим:

Соответственно,
наращивая сумму А
по ставке
i,
получим:

A(1+
i)ⁿ
= S. (4.3)

Пример
4.1. График
предусматривает следующий порядок
выдачи ссуды во времени: 1 июля 1994 г. —
5 млн. руб., 1 января 1995 г. — 15 млн. руб., 1
января 1997 г. — 18 млн. руб. Необходимо
определить сумму задолженности на
начало 1998 г. при условии, что проценты
начисляются по ставке 20%. Схематично
условия задачи показаны на рис 4.1.
Находим:

S
= 5 х 1,2^3,5
+ 15 х 1,2³
+ 18 х 1,2 = 56,985 млн. руб.

По этим же данным
определим современную стоимость потока
на момент выплаты первой суммы. При
прямом счете получим:

А
= 5 + 15 х 1,2^-0,5
+ 18 х 1,2^-2,5
= 30,104 млн. руб. или по формуле (4. 3)

А
= 56,985 х 1,2^-3,5
= 30,104 млн. руб.

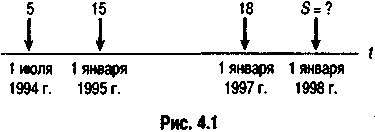
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основные выводы:

• Формула для расчета среднего процента – [(процент 1 + процент 2) (объем выборки 1 + объем выборки 2)] x 100

• Используйте средний процент при определении среднего значения двух или более процентов от целого.

Расчет среднего процента от чего-либо может показаться простой задачей, но эта концепция может быть сложнее, чем может показаться на первый взгляд. Хотя в некоторых случаях вы можете просто усреднить два процента, сложив их и разделив на количество используемых процентов, в других случаях вам может потребоваться учесть такие факторы, как размер выборки.

В этой статье мы обсудим проценты и способы вычисления среднего процента, а также приведем примеры использования формулы среднего процента в различных сценариях.

Понимание процентных соотношений

В базовом смысле проценты – это соотношение или доля чего-либо от 100. Например, если у вас есть коробка со 100 шоколадными конфетами и 35 из них наполнены ванильным кремом, это означает, что 35% шоколадных конфет имеют вкус ванильного крема. Проценты используются в различных аспектах повседневной жизни, в том числе в школе и на предприятиях. Расчет среднего процентного показателя также может быть использован в ряде различных сценариев. Например, инвестор может захотеть определить, как два разных запаса изменяются со временем по отношению друг к другу. Чтобы понять эту взаимосвязь, инвестору необходимо знать, как рассчитать среднее значение двух процентов запасов.

Как рассчитать среднее значение

Прежде чем мы сможем объяснить, как рассчитать средний процент, мы должны сначала определить, как рассчитать среднее значение. Среднее значение набора чисел – это просто сумма чисел, деленная на общее количество значений в наборе. Например, чтобы найти среднее значение 12, 15, 24, 78, 3, 313 и 10, просто сложите эти числа (12 + 15 + 24 + 78 + 3 + 313 + 10 = 455) и разделите на общее количество значений в наборе (7), чтобы получить среднее значение 65.

Как рассчитать средний процент

Вычисление среднего значения двух или более процентов требует иного набора шагов, чем определение среднего значения двух или более обычных чисел. При вычислении среднего процента необходимо учитывать несколько моментов, включая тот факт, что часто сначала необходимо вычислить реальные числа, которые представляет процент.

Для расчета среднего процента в большинстве случаев используйте следующие шаги:

1. Преобразуйте проценты, которые вы хотите усреднить, в десятичные числа

Первый шаг в вычислении среднего процентного показателя – перевести проценты в десятичные числа. Допустим, вы хотите определить среднее значение 30% от 150 и 25% от 200. Преобразуйте эти два процента в десятичные числа, разделив их оба на 100. Это означает, что 30% – это 0.3 как десятичная дробь и 25% – это .25 как десятичная дробь.

2. Определите число, которое представляет каждая десятичная дробь

После того, как вы перевели проценты в десятичные дроби, вам нужно найти число, которое представляет каждая десятичная дробь. Для этого нужно умножить десятичную дробь на общее количество в выборке. Таким образом, используя предыдущий пример, вы умножите 0.3 на 150, чтобы получить 45 и умножить .25 на 200, чтобы получить 50.

3. Сложите числа вместе

Следующим шагом будет сложение двух чисел, найденных на предыдущем этапе. Таким образом, 45 плюс 50 равно 95.

4. Сложите объемы выборки

Также необходимо сложить объемы выборки для каждого процента. Таким образом, 150 плюс 200 равно 350.

5. Рассчитайте среднее процентное значение

Чтобы найти средний процент из двух процентов в этом примере, нужно сначала разделить сумму двух процентных чисел на сумму двух объемов выборки. Итак, 95 разделить на 350 равно 0.27. Затем вы умножаете десятичную дробь на 100, чтобы получить средний процент. Итак, 0.27 умножить на 100 равно 27 или 27%. Это означает, что средний процент 30% от 150 и 25% от 200 составляет 27%.

Формула среднего процента

Ниже приведена формула, которая может быть использована для расчета большинства средних процентных показателей:

[(Процент 1 + процент 2)(объем выборки 1 + объем выборки 2)] x 100 = средний процент

В этой формуле процент 1 представляет собой десятичное значение данного процента от объема выборки 1. Чтобы определить значение процента 1, вы должны сначала преобразовать процент в десятичную дробь, а затем умножить десятичную дробь на размер выборки. Повторите этот шаг, чтобы определить десятичное значение процента 2 в этой формуле. После того как вы рассчитали десятичные значения каждого процента для каждого данного размера выборки, вы складываете эти десятичные значения вместе и делите полученное число на общую сумму обоих размеров выборки. Затем нужно умножить это значение на 100, чтобы получить средний процент.

Пример расчета средних процентов

Ниже приведен пример расчета среднего процента в реальных условиях:

Компания XYZ хочет определить средний процент того, сколько продуктов было продано из двух различных категорий продуктов в данном году. В первой категории товаров компания произвела 500 товаров и продала 75% из них. Во второй категории компания произвела 400 продуктов и продала 60% из них.

Для определения среднего процента проданных товаров из обеих категорий выполняются следующие действия:

1. Переведите оба процента в десятичные дроби. Итак, 75 разделить на 100 равно .75 и 60 разделить на 100 равно .60. Это дает вам .75 и .60 как представление двух процентов проданных продуктов из обеих категорий товаров.

2. Умножьте десятичные значения на общее количество продукции, произведенной в каждой категории. Итак,, .75 умножить на 500 равно 375 и .60 умножить на 400 равно 240. Это означает, что 75% от 500 составляет 375, а 60% от 400 равно 240.

3. Сложите два числа, которые представляют процентное соотношение товаров из каждой категории. Итак, 375 плюс 240 равно 615.

4. Сложите вместе общее количество продукции, произведенной в каждой категории. Так, 500 плюс 400 равно 900.

5. Разделите сумму процентов на сумму общего количества продуктов, произведенных в каждой категории. Так, 615, разделенное на 900, равно 0.68.

6. Умножьте десятичную дробь на 100, чтобы получить средний процент. Таким образом, 0.68 умножить на 100 равно 68, или 68%.

Используя эту формулу, компания XYZ продала в среднем 68% продуктов из двух категорий товаров, которые были проанализированы.

Для расчета среднего процента из нескольких процентных ставок нужно использовать взвешенное среднее арифметическое значение. Формула для расчета такого среднего значения будет выглядеть следующим образом:

средний процент = (сумма процентных ставок * доли каждой ставки) / сумма долей

где:

– сумма процентных ставок – сумма всех процентных ставок, которые нужно усреднить;
– доли каждой ставки – доля каждой процентной ставки от общей суммы процентных ставок;
– сумма долей – общая сумма долей всех процентных ставок.

Например, у вас есть инвестиции, где вы получили доходность 4% на 1000 долларов и 6% на 5000 долларов. Чтобы найти средний процент, используем формулу:

средний процент = (0,04 * 1000 + 0,06 * 5000) / (1000 + 5000) = 0,057 или 5,7%

Таким образом, средний процент для ваших инвестиций равен 5,7%.

Калькулятор среднего процента из нескольких процентов

Этот калькулятор позволяет пользователю ввести три пары значений: сумму и процентную ставку для каждой из трех инвестиций. После того, как пользователь нажимает кнопку “Рассчитать средний процент”, калькулятор вычисляет средневзвешенную процентную ставку на основе введенных значений.

Количество пар значений: