
Расчет теплот испарения и возгонки
Уравнение Клапейрона – Клаузиуса дает возможность определить тепловой эффект фазового перехода (в данном случае – испарения или возгонки) на основании экспериментальных данных о зависимости давления насыщенного пара (жидкой или твердой фаз) от температуры.
Расчет средней теплоты испарения или возгонки
|
Средней теплотой испарения или возгонки называется величина |
∆ |
, получаемая из |
|||
|
уравнения Клапейрона-Клаузиуса в приближении её постоянства( |
∆ф.п. = |
) в нешироком |
|||
|
интервале температур ( |
20 – 50 К). |
||||
|
Для расчета |
средней теплоты фазового перехода используются интегральные формы |
||||
|
∆ = |
уравнения Клапейрона-Клаузиуса, полученные в результате приближенного интегрирования: ln = ∆ф.п.
|
Принимаем ∆ = |
ln |
= |
∆ф.п. |
|||||||||||
|
и выносим за знак интеграла: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
Далее возможны два варианта интегрирования: |
||||||||||||||
|
1) Аналитический расчет |
||||||||||||||
|
Проводим определенное интегрирование указанного выражения: |
||||||||||||||
|
ln |
= |
∆ф.п. |
||||||||||||
|
В результате получаем расчетную формулу: |
||||||||||||||
|
ln |
= − |
∆ф.п. |
1 |
− |
1 |
|||||||||
|
где |
и – давления насыщенного пара соответственно при температурах |
и . |
||||||||||||
|
Таким |
образом, |
можно приближённо |
рассчитать среднюю теплоту |
испарения |
(возгонки) если известны хотя бы два равновесных давления пара при двух температурах.
Вместо давлений при двух температурах могут быть известны другие параметры, через которые давление можно выразить. Например, параметры состояния идеального газа: T, V, n.
1

2) Графический расчет Проводим неопределенное интегрирование уравнения и получаем уравнение прямой, не
проходящей через начало координат:
ln = − ∆ ∙ 1 +
|
Строим график в координатах |
и по тангенсу угла наклона прямой определяем |
||||||||||||||
|
или возгонки: |
|||||||||||||||
|
среднюю энтальпию испаренияln − |
= − |
∆ф.п. |
|||||||||||||
|
ф.п. |
|||||||||||||||
|
l |
− |
∆ф.п. |
= −2,303 ∙ |
∙ |
|||||||||||
|
координатах |
, то |
||||||||||||||
|
Если график построен в |
∆ |
= − |
∙ |
||||||||||||
|
Кроме того, уравнение прямой может быть представлено в виде |
|||||||||||||||
|
ln |
= + , где А и В |
||||||||||||||
|
– некоторые числовые коэффициенты. Тогда |
∆ф.п. |
= − ∙ |
. |
||||||||||||
Расчет истинной теплоты испарения или возгонки
При расчете истинного теплового эффекта испарения или возгонки (т.е. энтальпии фазового перехода при заданной конкретной температуре) используют дифференциальную форму уравнения Клапейрона-Клаузиуса.
ln = ∆ф.п.
или
= ∆ф.п.
Выражаем:
ln
∆ф.п. =
2

И далее задача сводится к нахождению производной, которую можно найти
аналитически или графически. 1) Аналитический расчет
Аналитический расчет возможен, если имеется функциональная зависимость вида
|
= |
( ) |
||||||||||||
|
. |
|||||||||||||
|
Например: |
|||||||||||||
|
где A, B, C, D – постоянныеlnкоэффициенты= + |
+ уравненияln + . |
||||||||||||
|
Дифференцируем данное выражение по температуре: |
|||||||||||||
|
ln |
|||||||||||||
|
Далее, |
умножаем на |
и |
получаем= − |
зависимость+ + |
теплоты фазового превращения от |
||||||||
|
температуры: |
ln |
||||||||||||
|
ф.п. |
ф.п. . |
||||||||||||
|
Подставляя в полученное∆уравнение= |
заданную температуру= − + , рассчитываем+ |
значение |
|||||||||||
|
Если имеется функциональная зависимость вида |
, то расчет |
теплового эффекта |
|||||||||||
|
∆ |
|||||||||||||
|
проводят по такому же принципу, с той лишь разницей, что=его( |
выражают из уравнения |
||||||||||||
|
) |
= ∆ф.п.
∆ф.п. =
2)Графический расчет
Взависимости от координат, в которых представлена графическая зависимость, расчет
∆проводится по соответствующему уравнению:
|
а) график в координатах |
∆ |
. |
|||||
|
В этом случае определение |
основано на уравнении: |
||||||
|
= ( |
) |
∆ф.п. |
|||||
|
ln |
= |
= |
|||||
|
Тангенс угла наклона касательной к графику в этих координатах равен: |
|||||||
|
Значит, |
= ∆ф.п.
3

Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной
∆ф.п. =
|
Если график построен в координатах l |
− |
, то |
|
∆ф.п. = 2,3
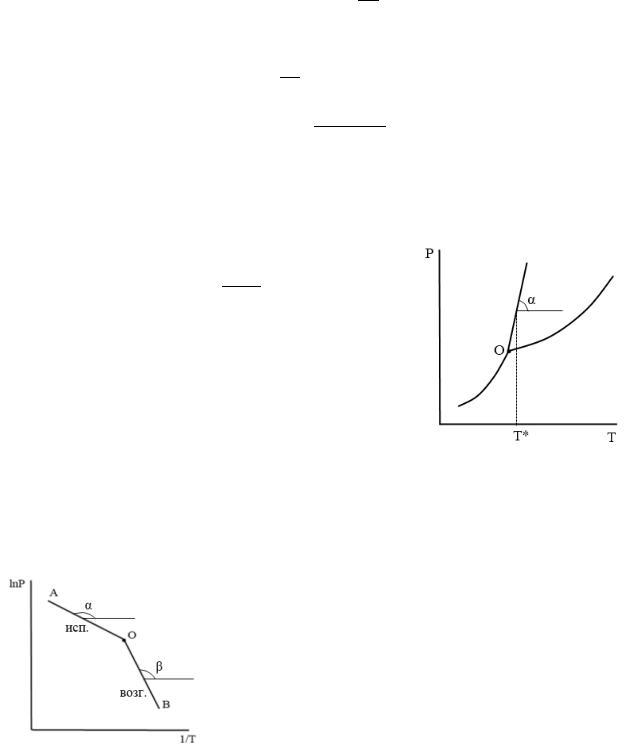
б) график в координатах = ( ).
Определение ∆ф.п. основано на уравнении:
= ∆ф.п.
Тангенс угла наклона касательной к графику в этих координатах равен:
=
= ∆ф.п.
Отсюда расчетная формула, связывающая тепловой эффект с тангенсом угла наклона касательной:
∆ф.п. =
Подставляя в это выражение найденный тангенс угла наклона касательной и конкретные значения Р* и Т*, находим тепловой эффект.
4
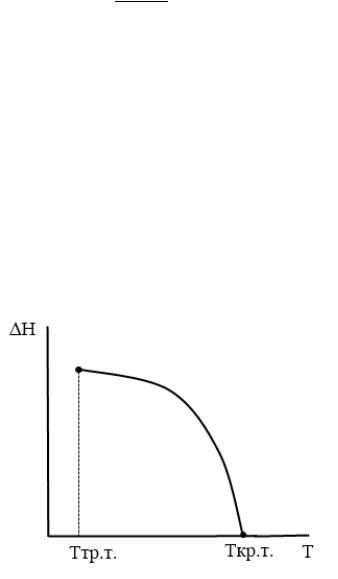
Зависимость теплоты испарения от температуры
Характер зависимости теплоты испарения от температуры определяется уравнением Кирхгофа:
∆исп. = ∆исп. . = ,пар − ,ж < 0
Следовательно, теплота испарения уменьшается с ростом температуры. В уравнении Кирхгофа записана производная функции одной переменной – температуры. В данной форме оно справедливо в той области температур и давлений, в которой пар можно считать идеальным газом и энтальпия испарения практически не зависит от давления. С приближением к критической точке для многих веществ пар становится неидеальным газом (например, у воды давление критической точки 218 атм и пар нельзя считать идеальным газом), но характер температурной зависимости энтальпии испарения сохраняется.
Графически эту зависимость в области температур существования жидкости (вдоль линии насыщенного пара) можно представить следующим образом:
График зависимости теплоты испарения от температуры начинается от температуры
тройной точки.
При низких и средних температурах теплота испарения убывает незначительно, от температуры практически не зависит.
По мере приближения к критической точке, эта зависимость становится все более ярко выраженной, наклон линии резко возрастает, и при критической температуре теплота испарения обращается в ноль:
|
∆исп. кр.т. = |
||||
|
Т.о. в области высоких температур зависимость |
||||
|
ln − будет отклоняться от прямолиней- |
||||
|
ной: |
||||
|
5 |

Правило Трутона
Теплоты испарения различных жидкостей закономерно связаны с их нормальными
температурами кипения.
Существует эмпирическое правило, которое носит название правила Трутона: Мольные
энтропии испарения неполярных неассоциированных жидкостей при нормальной
температуре кипения примерно одинаковы и в среднем составляют:
|
∆исп. = |
∆исп. |
≈ |
± |
Дж |
|
н.т.к. |
моль ∙ К |
В справочнике, на стр. 109 правило Трутона приведено в следующем виде:
|
∆исп. |
≈ , |
Дж |
|
н.т.к. |
моль ∙ К |
Это правило выполняется только для неполярных, неассоциированных в паровой фазе жидкостей и только при нормальной температуре кипения, которая у каждого вещества
единственная.
Интегрирование уравнения Клапейрона для процесса плавления
Т.к. мольные (удельные) объемы твердой и жидкой фаз очень близки друг другу по величине ( ж ≈ тв), уравнение Клапейрона для процесса плавления (а равно как и для процессов полиморфного превращения) преобразовать нельзя, и оно используется только в
таком виде:
= ∆пл.
∆
Или, что больше отвечает физическому смыслу процесса:
= ∆
∆пл.
Величина , определяющая наклон линии плавления к оси температур, хоть и является,
в свою очередь, функцией давления и температуры, но изменяется незначительно при
6

достаточно большом увеличении давления. Поэтому при изменении давления до 10 атм (иногда
|
и более) в хорошем приближении можно считать, что |
= |
, и линия плавления является |
||||||||
|
прямой линией. |
||||||||||
|
Соответственно, интегрирование уравнения Клапейрона-Клаузиуса для процесса |
||||||||||
|
плавления проводится следующим образом: |
∆пл. |
|||||||||
|
= |
||||||||||
|
приблизительно постоянная величина, рассчитанная, |
||||||||||
|
Cоотношение |
∆ |
берется как |
∆ |
|||||||
|
∆ |
||||||||||
|
например, при температуре , и выносится за знак интеграла: |
||||||||||
|
= |
∆пл. |
|||||||||
|
∆ |
∆
Другими словами, заменяем на ∆ .
|
∆ |
= |
∆пл. |
|
∆ |
||
|
− |
= |
∆пл. |
|
∆ |
||
|
= |
+ |
∆пл. |
|
∆ |
Так можно рассчитать, при каком давлении температура плавления станет равной ,
если известна при ,
или рассчитать температуру плавления при заданном давлении:
Расчет теплоты плавления
В основе – уравнение Клапейрона:
= ∆пл.
∆
1) Аналитический расчет Проводится по известной зависимости = ( ).
Пусть эта зависимость имеет вид:
=+ +
где А, В, С – постоянные коэффициенты уравнения.
Выразим теплоту плавления из уравнения Клапейрона:
7
∆пл. = ∆
Продифференцируем зависимость = ( ) по давлению:
=+ 2
∆
∆ = ( + 2 )
Подставляя в полученное выражение необходимые значения p и Т, находим ∆Н.
2) Графический расчет По наклону линии плавления:
|
= |
= |
∆пл. |
||
|
∆ |
||||
|
Отсюда выражаем ∆ |
: |
∆пл. = ∆
Подставляя сюда значение Т* и тангенса угла наклона линии плавления, получаем значение теплоты плавления.
3) Расчет теплоты плавления в тройной точке по теплотам испарения и возгонки
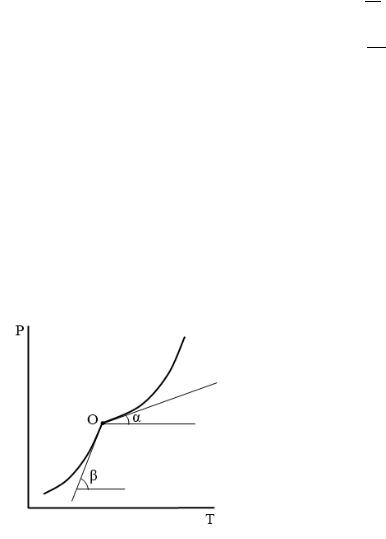
Находим теплоты испарения и возгонки по тангенсу угла наклона соответствующих прямых:
∆исп. = − ∙
∆возг. = − ∙
Затем находим теплоту плавления по соотношению:
∆пл. = ∆возг. − ∆исп.
ОА – линия испарения, ОВ – линия возгонки, т. О – тройная точка.
8
Если известны уравнения линий испарения и возгонки:
то можно найти теплоты испарения и возгонки через коэффициенты уравнений:
∆исп. = − ∙ и ∆возг. = − ∙ ′′
Теплоту плавления находим по разности теплот испарения и возгонки.
∆пл. = ( − )
Теплота плавления:
∆пл. = ∆возг. − ∆исп.
б) по графику − .
Проводим касательные к кривым испарения и возгонки в тройной точке:
|
∆исп. |
= |
|||||||||
|
∆возг. |
= |
|||||||||
|
В этих формулах Т и Р соответствуют температуре и |
||||||||||
|
давлению тройной точки. |
= ∆возг. − ∆исп. или: |
|||||||||
|
Теплота плавления: |
∆пл. |
|||||||||
|
∆пл. = |
− |
= |
( |
− |
) |
|||||
Расчет изменения внутренней энергии и энтропии при фазовых превращениях
|
Расчет изменения внутренней энергии |
и энтропии |
∆ |
для фазового перехода осуще- |
||
|
ствляется после того, как найдено значение |
теплового эффекта |
. |
|||
|
∆ |
∆ |
Изменение внутренней энергии
Рассчитывается по соотношению:
∆ф.п. = ∆ф.п. − ∆ф.п.
а) Плавление
∆пл. = 0
Следовательно
∆пл. = ∆пл.
9

б) Испарение, возгонка
∆исп.(возг.). = 1 ∆исп.(возг.) = ∆исп.(возг.) −
Для обратного перехода (конденсации):
∆конд = −1
∆конд. = −∆исп.(возг.)
Изменение энтропии
∆ф.п. = ∆ф.п.
Для конденсации:
∆конд. = −∆исп.(возг.)
10
Соседние файлы в предмете Физическая химия
- #
20.05.2020168.33 Кб3кр.png
- #
- #
20.05.2020933.47 Кб3лекции 1-5 фх
- #
- #
- #
- #
20.05.2020452.73 Кб2лекция 6
- #
20.05.2020596.4 Кб2лекция 7
- #
20.05.2020484.98 Кб1лекция 8
- #
- #
20.05.2020412.29 Кб1семинар 1
Испарение сопровождается остыванием жидкости. Чем она холоднее, тем менее интенсивно происходит образование пара. Но скорость процесса можно поддерживать, если жидкость подогревать, то есть подводить к ней тепло.
Так возникает понятие удельной теплоты парообразования. У каждого жидкости и даже твердого тела (ведь и его можно превратить в пар) эта величина своя. Рассмотрим, как найти удельную теплоту парообразования.
Содержание
- Единица измерения
- Формула для величины
- Какие данные нужны, чтобы рассчитать значение?
- Алгоритм и правила расчета
- Несколько примеров нахождения
- Таблица для ряда веществ
- Видео по теме статьи
- Заключение
Единица измерения
Удельная теплота парообразования – это величина, которая показывает, сколько теплоты необходимо сообщить веществу массой 1 кг, чтобы превратить его в пар. При этом температура вещества должна быть постоянной.
Обычно рассматриваемую величину обозначают латинскими буквами L, r или греческой λ (лямбда). Теплота в системе СИ измеряется в Джоулях (Дж), масса – в килограммах (кг). Таким образом, L измеряется в Дж/кг.
Так как теплота в джоулях принимает зачастую большие значения, может встречаться обозначения кДж (килоджоули) – Дж*1000, или МДж (мегаджоули) – Дж*1000 000.
Формула для величины
 Формула выглядит так: L = Q/m, где:
Формула выглядит так: L = Q/m, где:
- Q – теплота,
- m – масса.
Ее часто используют для расчетов энергетических затрат на выпаривание воды из растворов: Q= L* m.
L определяют в лабораториях и заносят в таблицы, составляют справочники, которыми можно пользоваться любому желающему. При этом всегда указывают температуру и давление, при которых находилось L.
С ростом температуры L уменьшается, так как жидкость расширяется, взаимодействие между ее частицами уменьшается, и ее легче превратить в пар. Когда плотность пара и жидкости сравниваются, наступает критическое состояние.
Оно характеризуется определенным давлением и температурой. Для воды — это 374 ℃ и 218,5 атм. В таком состоянии L=0.
Какие данные нужны, чтобы рассчитать значение?
Чтобы вычислить искомую величину, применяют знания о том, что теплота испарения равна теплоте конденсации со знаком «минус». Это значит, что когда пар конденсируется (превращается в воду), он охлаждается и отдает свое тепло окружающей среде. Можно применить формулу: Q= L* m.
Для расчетов необходимы следующие данные:
- Q – теплота, отданная паром, Дж,
- m – масса образовавшейся в процессе конденсации воды, кг;
- L – удельная теплота парообразования, Дж/кг – собственно то, что нужно определить.
Применяют также закон сохранения энергии и понятие теплоемкости: Qв=С*Mв*(T2-T1), где:
- С – удельная теплоемкость воды, которая нагревается под действием сконденсированного пара, Дж/(кг*К), – считается известной и берется из таблицы,
- Mв – ее масса;
- T2-T1 – изменение температуры в Кельвинах или градусах Цельсия.
Алгоритм и правила расчета
 Для решения большинства задач используют следующий алгоритм:
Для решения большинства задач используют следующий алгоритм:
- Анализируют, как проходит процесс, какое вещество отдает, а какое получает тепло.
- Переводят все единицы измерения в одну систему.
- Записывают необходимые формулы.
- Решают уравнение с одним неизвестным.
При проведении расчетов надо следить за размерностью величин. В системе СИ масса измеряется в кг, теплота в Дж, а температура в градусах Кельвина. Разность температур можно считать в градусах Цельсия.
Часто бывает нужно найти удельную теплоту парообразования при условиях кипения жидкости и нормальном атмосферном давлении (760 мм рт. ст.). В таких условиях получают чистую воду из растворов или выделяют из смеси веществ ее части.
Процесс используется в химической и пищевой промышленности и даже на бытовом уровне.
Несколько примеров нахождения
Задача №1. Сколько необходимо энергии для превращения в пар следующих кипящих веществ:
- 2 кг этилового спирта;
- 2 кг воды;
- 2 кг расплавленного свинца.
Необходимо воспользоваться формулой Q= L* m и взять значение L из таблицы. Получится:
- 0,84*МДж*2 кг = 1,68 МДж;
- 2,3 МДж*2 кг = 4,6 МДж;
- 8,6 МДж *2 кг = 17,2 МДж.
Как видно, превратить в пар воду сложнее, чем этанол, но легче, чем металл. На первый взгляд, это очевидно, но когда дело касается веществ, близких по температуре кипения, то разница становится менее заметна, ее невозможно угадать. Тем не менее, она имеет особое значение.
Задача №2. Как вычислить, сколько энергии необходимо, чтобы превратить 1 тонну воды при 20 ℃ в пар при 100 ℃?
Решение: 1 т = 1000 кг.
 Из закона сохранения следует, что общая энергия складывается из таких составляющих: Q = Q1 +Q2, где:
Из закона сохранения следует, что общая энергия складывается из таких составляющих: Q = Q1 +Q2, где:
- Q1 – тепло, ушедшее на нагревание воды с 20 до 100 градусов,
- Q2 – тепло, необходимое для образования пара (процесс происходит без изменения температуры).
Q1 = С*M* (T2-T1), С воды = 4200 Дж/(кг*К), Q2 = L*M, L воды при обычном кипении = 2,3 МДж/кг, T2-T1 = 100-20 = 80.
Подставляя известные величины, находят искомую энергию: Q = 4200*1000*80+2,3 *106*1000 = 4,2*80*106+2300*106=2636 (МДж)
Задача №3. Сколько надо затратить электроэнергии, чтобы превратить 1 л воды в пар?
Решение: Q= Lводы*m. Масса 1 литра обычной водопроводной воды равна 1 кг. Q=2260 кДж/кг *1 кг=2260 кДж=2,3 МДж.
1 кВт*ч = 3,6 МДж. Из простой пропорции следует, что надо затратить 0,64 кВт*ч. Для 2-х литров величина возрастет в 2 раза, для 3-х – в три, и так далее.
Зная тарифы на электроэнергию, несложно посчитать стоимость, во сколько рублей обойдется такое кипячение. Надо также учитывать, что частично энергия уйдет в воздух и на нагрев сосуда, частей плиты, поэтому реальный расход будет выше.
Таблица для ряда веществ
Удельная теплота парообразования при нормальном атмосферном давлении (1 атм = 760 мм рт. ст.) и температуре кипения (для каждого вещества она своя).
| Вещество | L, МДж/кг | T кипения, ℃ |
| Вода | 2,3 | 100 |
| Этиловый спирт | 0,84 | 78,4 |
| Метиловый спирт | 1,1 | 64,1 |
| Ртуть | 0,28 | 357 |
| Жидкий азот | 0,2 | -195,8 |
| Аммиак | 1,4 | -33,4 |
| Фреон 12 | 0,16 | -24,9 |
| Расплавленный алюминий | 10,9 | 2450 |
Для воды при 20 ℃ L=2,45МДж/кг.
Видео по теме статьи
Об удельной теплоте парообразования расскажет видео:
Заключение
Единица измерения удельной теплоты парообразования – Дж/кг. Она показывает, сколько при заданной температуре надо подвести тепла, чтобы преобразовать 1 кг вещества в пар. Величина определяется путем проведения экспериментов.
Для воды при 100 ℃ ее значение 2260 кДж/кг. Эта величина довольно большая в сравнении с характеристиками других веществ. С ростом температуры значение удельной теплоты образования пара уменьшается.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Цель работы: Определить среднюю теплоту испарения заданной легколетучей жидкости.
Мы знаем, что для измерения теплоты фазового перехода существуют колориметрические методы. Но в своей работе показали, что теплоту фазового перехода можно определить манометрическим методом по уравнению Клапейрона-Клаузиуса, измеряя температуру перехода жидкости в пар при разных значениях давления.
Жидкость, помещенная в сосуд, объем которого больше объема жидкости, начинает испаряться. Молекулы, покинувшие жидкость, диффундируют в находящийся над ней воздух. Если сосуд закрыт, то со временем между жидкостью и её паром устанавливается динамическое равновесие. Пар насыщен. Давление насыщенного пара зависит от температуры. С повышением температуры давление его увеличивается и может достигнуть давления воздуха над жидкостью. При этом, если в жидкости находятся пузырьки растворенного воздуха, жидкость начинает испаряется не только со своей поверхности, но и в пузырьки. Пузырьки разрастаются и всплывают – происходит кипение. При продолжительном кипении жидкость обедняется пузырьками, кипение прекращается, жидкость перегревается. При случайном появлении пузырьков, например, из пор стенок сосуда, кипение происходит со взрывом, при этом температура жидкости несколько уменьшается.В курсе термодинамики выводится уравнение, называемое уравнением Клапейрона-Клаузиуса:
(1)
Уравнение (1) связывает dP – изменение давления и dT – изменение температуры с – удельной теплотой перехода из одного агрегатного состояния в другое. Применим уравнение (1) к переходу жидкость-газ.
Объём газа с некоторым приближением можно взять из уравнения Клапейрона-Менделеева:
.
Тогда получим другой вид уравнения (1):
Теплота испарения сравнительно слаба зависит от температуры , можно считать постоянной и пользоваться интегральной формой уравнения:
(2)
Уравнение (2) в координатах lnP и представляет собой прямую линию с угловым коэффициентом .
Определив из графика уравнения (2) значение углового коэффициента и приравняв его , легко вычислить .
1. Сосуд с испытуемой жидкостью.2. Обратный холодильник.3. Водяной термостат.4. Термометр.5. Сушилка-сосуд, заполненный.6. Ртутный манометр.7. Маностат.8. Игольчатый клапан.9. Вакуумный клапан.
Выполнение работы:
1.Обогащают воздухом испытываемую жидкость, для этого:а) частично откачивают из системы воздух ;б) открывают кран игольчатого клапана (8) и очень медленно впускают в систему воздух из атмосферы.2. Нагревают воду термостата до 75° и ждут 5-7 мин. Для того, чтобы жидкость в сосуде (1) приняла температуру термостата.
3.Откачивая воздух из системы, заставляют испытываемую жидкость закипеть. В момент кипения (появление 3-4 пузырьков из глубины жидкости) фиксируют температуру кипения и высоты и уровней ртути в манометре, не давая жидкости долго кипеть.
Для прекращения кипения немного увеличивают давление в системе4. Понижая температуру воды в термостате, вначале на 5-7°, а начиная с 50° – на2-3° путем доливания холодной воды производят 12-15 аналогичных измерений.
Данные измерений представляют в таблице 1.
Табл. 1.
∆H ист =2.3* tg α*R
Tg α =5.25/3.186=1.65
∆H ист =2.3*1.65*8.31=31,54 КДж
Вывод: молярная теплота фазового перехода была определена в интервале температур-от 37 до 52 °С и среднее значение составило 31,54 КДж.
Список использованной литературы.
- Миронов Г.С. «Основной органический синтез и нефтехимия Выпуск 5»
-
Физическая и коллоидная химия Учебник для ВУЗов, Хмельницкий Р.А., 2009г.
-
Физическая химия Учебник для ВУЗов, Зимон А.Д., 2006г.
-
Физическая химия, Стромберг А.Г., 2009г.
-
Н.К. Воробьёв, В.А. Гольцшмидт, М.Х. Карапетьянц
-
«Практикум по физической химии», Государственное научно-техническое
-
издательство химической литературы, Москва, 1950
Определение теплоты испарения жидкости
Для равновесия между жидкостью и паром уравнение Клапейрона-Клаузиуса может быть получено следующим образом.
Согласно второму закону термодинамики если система находится в равновесии, то при данных условиях (Р, Т) работа не совершается
то есть свободные энергии Гиббса чистой жидкости и её пара равны (это условия равновесия).
Изменим одно из условий, определяющих равновесие, например, температуру (то есть нагреем систему на Т), в результате этого установится новое давление, новое равновесие жидкость-пар:
Если изменение внешнего параметра произойдет на бесконечно малую величину – dT, то и изобарно-изотермические потенциалы изменятся на бесконечно малую величину:
Изобарно-изотермический потенциал представляет собой свободную энергию системы и является функцией давления и температуры:
поэтому с его помощью можно установить количественную зависимость между давлением насыщенного пара и температурой.
После подстановки (6) в (5) имеем в состоянии равновесия
VжdP – SжdT = VпdP – SпdT (7)
откуда 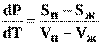 (8)
(8)
где (Sп – Sж) и (Vп– Vж) – изменение соответственно энтропии и объема системы при переходе вещества из жидкого в парообразное состояние. Согласно второму закону термодинамики изменение энтропии системы при испарении равно приведенной теплоте испарения
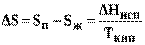 (9)
(9)
Подставив выражение (9) в (8) получим
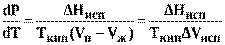 (10)
(10)
где ∆Hиспи ∆Vисп– соответственно изменение энтальпии и объема при испарении, аTкип– температура кипения.
Уравнение (10) называется уравнением Клапейрона-Клаузиуса. Согласно (10) наклон линий на фазовой диаграмме воды (рис. 1) определяется знаком производнойdP/dTили обратной ей величиныdT/dP– характеризующей изменение температуры с увеличением давления.
Из фазовых переходов рассмотрим испарение и плавление. Теплота испарения – перехода жидкой фазы в газообразную положительна. Молярной теплотой испаренияназывается количество тепла, затраченное на испарение одного моля жидкого вещества. Объем газа при испарении всегда больше соответствующего объема жидкости, то есть в уравнении (10)Vп> Vж. ПоэтомуdP/dT, а значит, иdT/dPтакже всегда положительны (dT/dP> 0). Следовательно, температура испарения всегда повышается с ростом давления (криваяОКна рис. 1 или см. табл. 1 Приложения). С увеличением температуры давление насыщенного пара над жидкостью возрастает, принимая максимальное значение при критической температуре. Последняя является предельной температурой (например, для воды она равна 374,12 о С) при которой возможно равновесие между жидкой и паровой фазой вещества. При более высоких температурах вещество может находиться только в газообразном состоянии, и понятие насыщенного пара теряет свой смысл.
Теплота плавления – перехода твердой фазы в жидкую также всегда положительна.
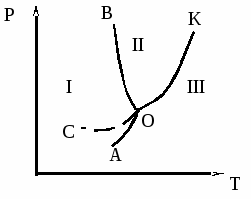 Рис. 1. Диаграмма состояния воды при невысоких давлениях
Рис. 1. Диаграмма состояния воды при невысоких давлениях
Области: 1 – твердая фаза (лед); II- жидкость; III – пар.
Кривые: АО – возгонки; ОК – испарения; ОВ – плавления.
О – тройная точка, отвечающая равновесию трех фаз.
Объем жидкой фазы в общем случае может быть больше или меньше объёма того же количества твердой фазы. Отсюда в соответствии с уравнением (10) вытекает, что величина dP/dTили обратная её величинаdT/dP, может быть положительной или отрицательной. Это значит, что температура плавления может повышаться или снижаться с увеличением давления. ВеличинаdT/dPположительна для большинства веществ. Она имеет отрицательное значение лишь для воды, висмута и немногих других веществ, для которых плотность жидкости при температуре плавления больше плотности твердой фазы (Vж–Vт) > 0 (например, для воды мольный объём в парообразном состоянии при н.у.Vп≈ 22400 см 2 , а в жидком состоянииVж≈ 18 см 3 ), то без большой погрешности можно пренебречь величинойVжи принять, что∆Vисп≈Vп.
2) При не слишком высоких давлениях и температурах (вдали от критических) можно применять уравнение состояния для идеальных газов и к реальным системам. Погрешность, получаемая при этом, оказывается незначительной.
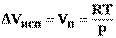 (11)
(11)
Подставив (11) в (10) получим:
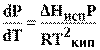 (12)
(12)
которое после преобразования
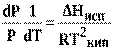 (13)
(13)
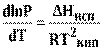 (14)
(14)
Теплота испарения зависит от температуры: с повышением температуры теплота испарения понижается. При критической температуре теплота испарения равна нулю. Однако при температурах, далеких от критической, изменения∆Ниспс температурой не очень велики. В не слишком большом интервале температур∆Ниспможно считать постоянной.
Интегрирование уравнения Клапейрона-Клаузиуса (14) в пределах температур Т1 иТ2, которым отвечают давленияР1 иР2 при постоянном значении ∆Нисп, дает
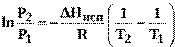 (15)
(15)
или при переходе к десятичным логарифмам
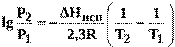 (16)
(16)
(R– универсальная газовая постоянная равная 8,314 Дж/моль · К).
Уравнения (15), (16) позволяют рассчитать теплоту испарения. Для этого по экспериментальным данным строят зависимость lnP=f(1/T) илиlgP=f(1/T) и на полученной прямой выбирают две точки (рис. 2). Подставляют соответствующие этим точкам значения логарифма давления и обратной температуры в уравнение (17):
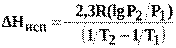 (17)
(17)
Значение∆Нисппо уравнению (17) зависит от взятого интервала температур и тем ближе к истинному, чем этот интервал меньше. Однако для такого вычисления требуется весьма точное измерение температуры кипения и давления пара.
Для вычисления∆Ниспв относительно широком интервале температур (50. 100 о С) следует выбирать точки, наиболее точно укладывающиеся на прямуюlgP=f(1/T).
Температура кипения жидкости, давление пара при данной температуре и теплота испарения являются специфическими константами вещества, значения которых необходимы для многих теоретических и практических расчетов. На основе этих данных можно определять чистоту химических веществ, провести расчет разделения смесей путем перегонки, рассчитать энергетические затраты на испарение жидкости, необходимые для проведения реакции в газовой фазе.
Зависимость теплоты испарения жидкости от температуры
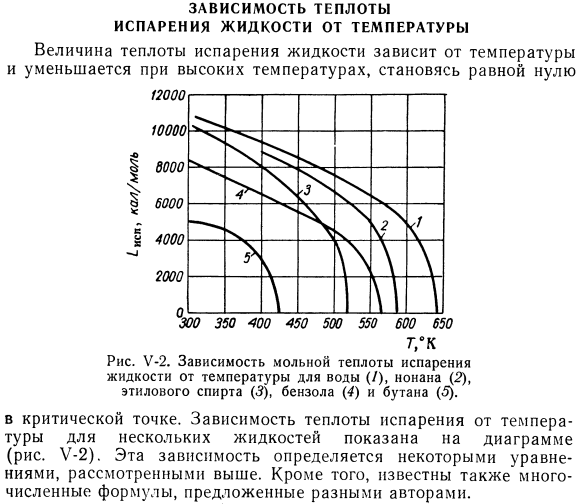


Зависимость теплоты испарения жидкости от температуры
Зависимость теплоты испарения жидкости от температуры. Теплота испарения жидкости зависит от температуры, при высоких температурах она уменьшается и становится равной нулю В важный момент.
Теплота испарения с увеличением давления, а следовательно, и температура кипения жидкости, уменьшается. Людмила Фирмаль
- Температурная зависимость некоторых жидкостей от теплоты испарения показана на рисунке (рисунок U-2). Эта зависимость определяется некоторыми из рассмотренных выше уравнений. Кроме того, известно также большое количество формул, предложенных разными авторами.
Поэтому значения теплот испарения определяют обычно опытным путем и при тех или иных тепловых расчетах требуемые данные берут из справочных таблиц. Людмила Фирмаль






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Фазовые переходы и уравнение теплового баланса
теория по физике 🧲 термодинамика
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
Определение Отвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Парообразование и конденсация
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
Определение Конденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Тепловые процессы при нагревании и охлаждении
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
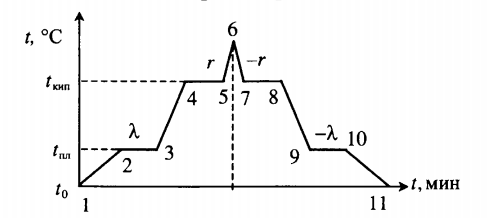
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
Q = c т m ( t п л − t 0 )
ст — удельная теплоемкость вещества в твердом состоянии.
Q = c ж m ( t к и п − t п л )
сж — удельная теплоемкость вещества в жидком состоянии.
Q = c п m ( t − t к и п )
сп — удельная теплоемкость вещества в газообразном состоянии.
Q = c п m ( t к и п − t )
Q = c ж m ( t п д − t к и п )
Q = c т m ( t 0 − t п л )
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела | |
| 2–3 | Плавление при температуре плавления (tпл) | |
| 3–4 | Нагревание жидкости | |
| 4–5 | Кипение при температуре кипения (tкип) | |
| 5–6 | Нагревание пара | |
| 6–7 | Охлаждение пара | |
| 7–8 | Кипение при температуре кипения (tкип) | |
| 8–9 | Охлаждение жидкости | |
| 9–10 | Отвердевание при температуре плавления (tпл) | |
| 10–11 | Охлаждение твердого тела |
Q = c л m ( t п л − t л ) + λ m
cл — удельная теплоемкость льда, tл — начальная температура льда.
Q = c л m ( t п л − t л ) + λ m + c в m ( t в − t п л )
cв — удельная теплоемкость воды.
Q = λ m + c в m ( t к и п − t п л ) + r m
Q = c в m ( t к и п − t в ) + r m 2 . .
Подсказки к задачам
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 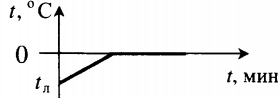 |
|
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 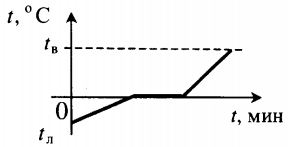 |
|
| Взяли лед при температуре 0 о С и полностью испарили. | 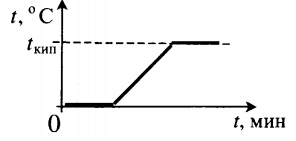 |
|
| Взяли воду при комнатной температуре и половину превратили в пар. | 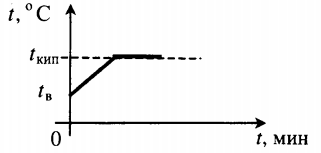 |
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 о С. |
| Объем воды 5 л | m = 5 кг, так как:
m = ρ V =10 3 · 5 · 10 − 3 м 3 = 5 к г Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 о С, чтобы превратить его в воду и нагреть ее до температуры +30 о С?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q = Q 1 + Q 2 + Q 3
Q = c л m ( 0 − t 1 ) + λ m + c в m ( t 2 − 0 )
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙10 3 Дж/кг.
Q = 2050 · 2 ( 0 − ( − 10 ) ) + 333 , 5 · 10 3 · 2 + 4220 · 2 · 30 = 961200 ( д ж ) = 961 , 2 ( к Д ж )
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Q о т д = − Q п о л
Отданное количество теплоты меньше нуля (Qотд 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 о С. Учтите, что лед плавится, если он находится при температуре 0 о С и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 о С, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 о С, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 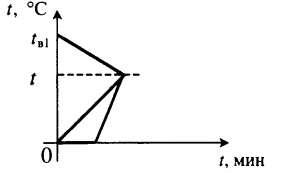 Уравнение теплового баланса: Уравнение теплового баланса:
Q 1 + Q 2 + Q 3 = 0 c в m в 1 ( t − t в 1 ) + c в m в 2 ( t − 0 ) + λ m л + c в m л ( t − 0 ) = 0 |
||||||||||||||
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 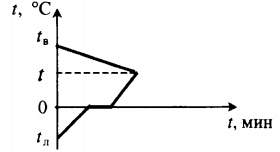 Уравнение теплового баланса: Уравнение теплового баланса:
c в m в ( t − t в ) + c л m л ( 0 − t л ) + λ m л + c в m л ( t − 0 ) = 0 |
||||||||||||||
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 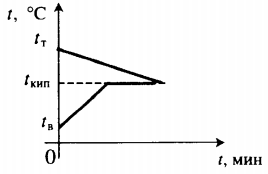 Уравнение теплового баланса: Уравнение теплового баланса:
c т m т ( 100 − t т ) + c в m в ( 100 − t в ) + r m п = 0 |
||||||||||||||
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 о С. | 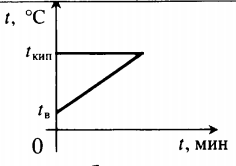 Уравнение теплового баланса: Уравнение теплового баланса:
− r m п + c в m в ( 100 − t в ) = 0 |
||||||||||||||
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 о С. |  Уравнение теплового баланса: Уравнение теплового баланса:
− r m п + c в m п ( t − t к и п ) + λ m л + c в m л ( t − t п л ) = 0 Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 о С, долили 3 л кипятка. Какая температура воды установилась? Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому: c m 1 ( t − t 0 ) = − c m 2 ( t − t к и п ) m 1 ( t − t 0 ) = − m 2 ( t − t к и п ) m 1 t + m 2 t = m 1 t 0 + m 2 t к и п ( m 1 + m 2 ) t = m 1 t 0 + m 2 t к и п t = m 1 t 0 + m 2 t к и п m 1 + m 2 . . t = 2 · 25 + 3 · 100 2 + 3 . . = 350 5 . . = 70 ( ° C ) Взаимные превращения механической и внутренней энергииЕсли в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале. Частные случаи закона сохранения энергии m v 2 2 . . = c m Δ t 0 , 5 ( m v 2 0 2 . . − m v 2 2 . . ) = c m Δ t m v 2 2 . . = c m Δ t + λ m 0 , 6 m g h = c m Δ t + r m q m т о п = m р g h 0 , 25 q m т о п m с v 2 2 . . Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К). Запишем закон сохранения энергии для этого случая: 0 , 52 m v 2 2 . . = c m Δ t Δ t = 0 , 52 v 2 2 c . . = 0 , 52 · 100 2 2 · 130 . . = 20 ( К ) Примеры КПД
Q п о л е з н = c m Δ T Q п о л е з н = c m Δ T + r m ( п р о и з в е д е н и е м о щ н о с т и н а в р е м я ) η = c m Δ T P t . . 100 % Q п о л е з н = c m Δ T Q з а т р = q m т о п η = c m Δ T q m т о п . . 100 % A п о л е з н = N t = N s v . . Q з а т р = q m т о п η = c m Δ T v q m т о п . . 100 E п о л е з н = m v 2 2 . . Q з а т р = q m п о р η = m v 2 2 q m п о р . . 100 Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна: Q 1 t 1 . . = Q 2 t 2 . . Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 о С потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг. Будем считать, что мощность электроплитки постоянна. Поэтому: Q 1 t 1 . . = Q 2 t 2 . . Количество теплоты, сообщенное воде при нагревании: Q 1 = с m ( t 2 − t 1 ) Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась: с m ( t 2 − t 1 ) t 1 . . = r m t 2 . . Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь. Алгоритм решения Решение Запишем исходные данные: Составим уравнение теплового баланса для первого случая: Q 1 = λ m + c m t 1 Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0. Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 о С. pазбирался: Алиса Никитина | обсудить разбор | оценить Внимательно прочитайте текст задания и выберите верный ответ из списка
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера. Ответ: а) Температура плавления первого тела в 1,5 раза больше, чем второго. б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. г) Оба тела имеют одинаковую удельную теплоту плавления. д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии. Алгоритм решения
Решение Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго. Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго. Первое утверждение неверно. Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так. Второе утверждение неверно. Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки. Третье утверждение верно. Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления. Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки. Четвертое утверждение верно. Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии. Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так. Пятое утверждение верно. Вывод: верным утверждения «в» и «д». pазбирался: Алиса Никитина | обсудить разбор | оценить В сосуде лежит кусок льда. Температура льда t 1 = 0 “> t 1 = 0 °C. Если сообщить ему количество теплоты Q = 50 “> Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t 2 = 20 “> t 2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь. [spoiler title=”источники:”] http://lfirmal.com/zavisimost-teploty-ispareniya-zhidkosti-ot-temperatury/ [/spoiler]
|
Приводимые в табл. XII значения теплот образования паров углеводородов Е большинстве случаев вычислены но экспериментально найденным теплотам образования жидких углеводородов и теплотам испарения, вычисленным на [c.309]
Для МНОГИХ веществ уравнение (П.4) удовлетворительно выполняется в небольшом интервале температур и его достаточно часто применяют для ориентировочного определения теплот испарения. Обычно теплоты испарения, вычисленные по уравнению (II.4), отличаются от значений, полученных в прямых калориметрических опытах, на 3—5 %. [c.24]
Теплота испарения, вычисленная по уравнению (У-З), равна 7490 кал/моль. [c.165]
По данным других авторов , теплота испарения, вычисленная по давлению пара синильной кислоты, в интервале О—25 °С составляет 6,61—6,65 ккал/моль. Константа Трутона — молекулярная теплота испарения при температуре кипения Т — температура кипения, °К) равна 21,8 кал (град-моль). [c.15]
Обработка проведена по тому же плану, что и в [4]. Для каждого углеводорода вначале приводится литературный материал по экспериментальным и вычисленным значениям теплот испарения Затем дается сводная таблица, в которой указаны молярные теплоты испарения, вычисленные по данным различных авторов при ровных значениях температур, н. т. и = 25° С. В таблицу включены и значения//, рассчитанные [6] по приближенному уравнению [c.279]
Вообще говоря, скрытая теплота испарения должна уменьшаться с повышением температуры. Колебания вычисленных нами величин в интервале 7800—9200, около средней величины порядка 8500, объясняются неточностью экспериментальных данных, положенных в основу расчета. В этом можно убедиться, выполнив аналогичный расчет по уравнению Питцера и Скотта [9] [c.10]
В этом случае, когда зависимость упругости пара вещества дана в виде эмпирического уравнения, вроде уравнения (13), вычисление величины скрытой теплоты испарения может быть осуществлено более простым путем. [c.10]
Средние величины скрытых теплот испарения различных жидкостей, вычисленные по уравнениям (17а), (18а), (19а), (20а) п (21а) [c.11]
В заключение следует упомянут ., что в 1951 г. П. Л. Чу и С. С. Чин предложили обобщенное уравнение для вычисления скрытой теплоты испарения [c.12]
Авторы утверждают, что П1)и вычислении скрытой теплоты испарения по их уравнению ошибка не превышает 5%. [c.12]
Этот результат более точен, чем предыдущий, так как вычислен на основании пяти опытов (истинное значение теплоты испарения метана при нормальной температуре кипения 8,19 кДж/моль). [c.158]
Если же щелочное плавление проводится в открытых котлах с применением раствора едкого натра, который подвергается предварительному упариванию, определение (Зз сводится к вычислению теплоты испарения воды из щелочного раствора. Эго вычисление может быть сделано по методу, описанному в главе I, однако для практических расчетов удобнее пользоваться [c.331]
Для вычисления теплосодержания смеси паров воды и аммиака иногда находят теплоту испарения этой смеси как сумму теплот иснарения воды и выделения аммиака из водного раствора. Тепло выделения NH., из раствора может быть принято по данным табл. 15 (стр. 382). [c.385]
Более или менее интенсивные взаимодействия между частицами, составляющими раствор, вызывают в растворах отклонения от идеального поведения. Положительные отклонения от закона Рауля присущи системам, в которых силы взаимодействия между однородными частицами (А—А или В—В) больше, чем между разнородными (А—В). Это бывает при различии в полярности компонентов раствора, особенно, если одно из веществ ассоциировано. Тогда образование раствора сопровождается обычно поглощением теплоты в связи с этим уменьшается теплота испарения компонентов из раствора, что облегчает испарение. Поэтому давление пара над системой оказывается большим, чем вычисленное по закону Рауля. [c.92]
Значительно реже отрицательные отклонения от закона Рауля. Они проявляются, если силы взаимодействия между однородными частицами (А—А или В—В) меньше, чем между разнородными (А—В). В этом случае образование раствора обычно происходит с выделением теплоты, в связи с чем теплота испарения увеличивается. Это затрудняет процесс испарения, и давление пара над системой оказывается меньшим, чем вычисленное по закону Рауля (рис. VII. 4). [c.93]
Давления паров диэтилового эфира при 20 и 30° С соответственно равны 58 945 и 86 285 Па. Рассчитать среднюю теплоту испарения эфира (Дж/г) в указанном интервале температур. Сравнить полученный результат с вычисленным по приближенной формуле Трутона . Температуру кипения эфира найти в табл. 8 приложения. [c.76]
Уравнение Клапейрона — Клаузиуса является в руках опытного физико-химика чрезвычайно полезным инструментом, позволяющим производить весьма разнообразные расчеты. Может быть, наиболее удивительной является возможность вычисления калориметрической величины — теплоты испарения — из давления пара, т. е. данных по сути дела механических. [c.102]
Другой способ приближенного вычисления давления пара требует знания теплоты испарения и температуры кипения. Так, для алюминия теплота испаре- [c.45]
Аналогичные вычисления легко осуществить и для других превращений. Из результатов следует, что теплоты плавления, перехода из одной модификации в другую, из аморфного состояния в кристаллическое составляют величины порядка 4 — 12 кДж/моль, теплоты испарения до 42 кДж/моль. [c.86]
Ур-ние (1) применяют для приближенного определения зависимости теплот испарения и сублимации от т-ры. В этих случаях АСС — С (или — С “). Однако при точных вычислениях следует учитывать, что с изменением т-ры равновесное давление двухфазной системы изменяется. Ур-ния (1) и (2) выведены Г.Р. Кирхгофом в 1858. [c.387]
Ионные кристаллы характеризуются электростатическими силами, действующими между ионами. Энергия решетки, определяемая из измерений теплоты образования и теплоты испарения, соответствует энергии, вычисленной в предположении, что узлами решетки являются ионы, удерживаемые электростатическими силами. [c.586]
ВЫЧИСЛЕННАЯ СКРЫТАЯ ТЕПЛОТА ИСПАРЕНИЯ ХЛОРИСТОГО ВИНИЛА [c.200]
Коэффициент при х может быть вычислен непосредственно по принятому значению djD, скрытой теплоте испарения ВКК iw и по величине коэффициента обогащения т. Пусть его вели- [c.384]
Сравнение значений отношения теплоты испарения при температуре кипения под давлением р = 1 атм к этой же температуре ( ,1сп/Ткип)1 вычисленных различными методами 19] [c.179]
Теплота испарения, вычисленная на основании зависимостей упругости пара от температуры по уравнению Клаузиуса—Клаиие-1ро “а для Б11Ц, ратиз 8,73 ккал/моль рассчитанная по правилу Трутоиа — 8,28), а для ДМЦ — 9,78 ккал/моль (по Трутону — 9,27). [c.89]
Экстраполированная т. кип. равна 47,5°. Скрытая теплота испарения, вычисленная по уравнению Клаузиуса—Клапейрона, равна 7,1 ккал [142]. Плотность жидкого OsFg при температуре кипения равна [143] 2,74 0,04. Молекулярный вес пара OsFg близок к нормальному. [c.609]
Следует отметить, что теплоты сублимации IF7, вычисленные по уравнениям связи между давлением насыщенного пара и температурой, приведенным в работах [175, 287], равныз 7,33 [287] и 7,51 [175] ккал/моль. Теплота сублимации, вычисленная по данным работы [292], равна 6,0 ккал/моль, т. е. меньше вышеуказанных теплот сублимации, и близка к теплоте испарения, вычисленной по данным этой же работы [292] и работы [296]. [c.19]
Этот расчет производился для смешения двух жидкостей, но ясно, что, поскольку каучук при растворении ведет себя по существу как жидкость, то для растворов каучука можно применить тот же метод. Главная трудность возникает при определении удельной энергии когезии в каучуке. Для жидкости удельная энергия когезии представляет собой просто скрытую теплоту испарения, вычисленнию на кубический сантиметр при постоянном объеме. Приближенное значение для каучука может быть получено из рассмотрения его молекулярной структуры. Удельные энергии когезии парафинов С Нг +2 растет с длиной цепи и, повидимому, стремятся к предельному значению порядка 60 кал/ см , по мере того как растет п. Присутствие метильных боковых групп в каучуке должно несколько снизить эту величину, тогда как двойные связи вызывают небольшой [c.160]
Применение закона Гесса избавляет от проведения большого числа излищних экспериментов в термохимии (так называется раздел химии, посвященный теплотам реакций и энергетическим свойствам веществ). Совершенно не обязательно измерять и табулировать изменение энтальпии каждой возможной химической реакции. Например, если известны теплота испарения жидкой воды [уравнение (2-10)] и теплота разложения пероксида водорода с образованием жидкой воды [уравнение (2-9)], то совсем не обязательно измерять теплоту разложения пероксида водорода с образованием водяного пара эту величину гораздо проще получить путем вычислений. Если какая-либо интересующая нас реакция трудно поддается проведению в лабораторных условиях, нужно попытаться подобрать последовательность легче осуществляемых реакций, сумма которых дает необходимую реакцию. После измерения изменений энтальпии для всех индивидуальных реакций в такой последовательности можно просуммировать соответствующие изменения энтальпии подобно самим химическим уравнениям и найти теплоту труднопроводимой реакции. [c.92]
Если же исп неизвестна, то необходимо знать давления при двух температурах и, подставив их в ур. (VIII, 10), получить два уравнения с двумя неизвестными ( исп и С), которые легко определяются путем решения системы этих двух уравнений. Подставляя найденные значения в ур. (VIII, 10), получаем возможность применить его как для определения давления при заданной температуре, так и для обратного расчета. Вычисленные значения сп часто обладают практически такой же точностью, как получаемые непосредственным измерением теплоты испарения. [c.254]
Используя термодинамические соотношения теории объемного заполнения, развитые Берингом и Серпинским [12,15], были определены дифференциальные теплоты адсорбции н-парафинов. На рис.З представлены сравнительные данные по теплотаы адсорбции н-додекана цеолитом МдА, вычисленным в виде изостерических теплот адсорбции по известному уравнению [16] и дифференциальным теплотам адсорбции, рассчитанным по уравнению, полученному сочетанием уравнения пейрона-Клаузиуса для теплоты испарения и уравнения (1) [17] [c.15]
Вычисление геплс ем лости,, теплового эффекта процессов, теплот испарения и плавления подробно описано в курсе химической термодинамики. ЗдесЕ. оно ),чсх гатрено лишь в объеме, необходимом для выполнения [ ловых расчетов основных аппаратов промышленности органических полупродуктов и красителей. [c.73]
Это соотношение используют либо для расчета давления пара по известным теплотам испарения или сублимации, либо для вычисления теплоты по давлению пара, измеряемому экспериментально. Для процессов сублимации твердых тел и испарения жидкостей переход в газовую фазу связан с преодолением энергии межмолекулярного взаимодействия. Поэтому L = Hr—Яконд >0. В соответствии с (IV.5) давление пара растет с температурой экспоненциально. [c.123]
Недостаток описанной программы заключается в том, что не учитываются изменения параметров вследствие измененин состава. Например, если компоненты разделяемой бинарной смеси имеют неодинаковые теплоты испарения, то в переходном режиме изменяются также М/, , Л1 , и т] . Аналогичное влняние изменений давления на состав и поток не учитывается. Эти изменения можно ввести в расчеты таким образом, что после определенного числа шагов вычисления прерываются, вводятся новые вычисленные параметры и затем вычисления продолжаются. [c.503]
Так как уравнение ван-дер-Ваальса только приближенное, то значенпп константы зависят от физических данных, использованных для ее вычисления. Приведенные в таблице данные основаны на критических свойствах. Значения, полученные из теплоты испарения и плотности ншдкости в точке кипения при атмосферном давлении, в два или три раза больше, хотя соотношение это уменьшается с повышением точки кипения. [c.85]
Для вычисления величин скрытых теплот испарения фракций смол коксования в техническом справочнике коксохимической промышленности [29] рекомендована формула Крэга. Однако она находится в непримиримом противоречии с цифро-вьш материалом, по-лаещенном в таблицах этого же справочника. Эмпирическая формула Крэга выведена для теплот [c.136]
Для обобщения представлений, которые были получены на основании упомянутых экспериментальных данных, необходимо чисто теоретическое обсуждение положения дел. Соответствующий анализ был произведен Г. Бауле [44] и позднее Ленгмюром 41]. Однако в новой важной работе М. Поляни и Е. Вигнера [45] удалось продвинуться дальше. Правда, они разработали только случай одинаковых атомов и равных сил связи, но это как раз соответствует процессам испарения и конденсации, которые и подлежат здесь специальному обсуждению. Колебания энергии внутри системы жестко друг с другом связанных атомов происходят из-за интерференции собственных колебаний. Вычисления показывают, что в течение времени одного колебания (l/v) изменение на одной связи составляет в среднем – кТ, и что для накопления энергии Е > кТ необходимо в среднем время ех])(Е/кТ). До удаления одного атома, связанного в трех направлениях, протекает в среднем время 2 ) (кТ1Е) X X ехр( /Л 7 ). Отсюда получается, что скорость испарения с 1 см тюверхпости составляет (2у/б ) К/кТ)ех ) К/кТ), если через 6 обозначить площадь поверхности, занимаемую одним атомом, а работу отрыва Е заменить равхшй ей атомарной теплотой испарения X. [c.38]
Более точный метод расчета мольной теплоты испарения вещества, основанный на принципе суммирования долей, заключается в вычислении значения лиопарахора [c.169]
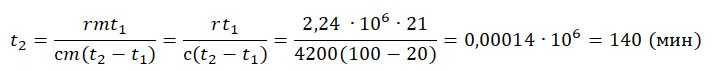
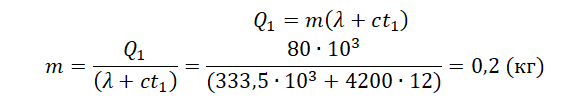
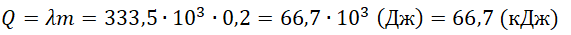
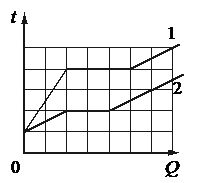 На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.