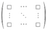
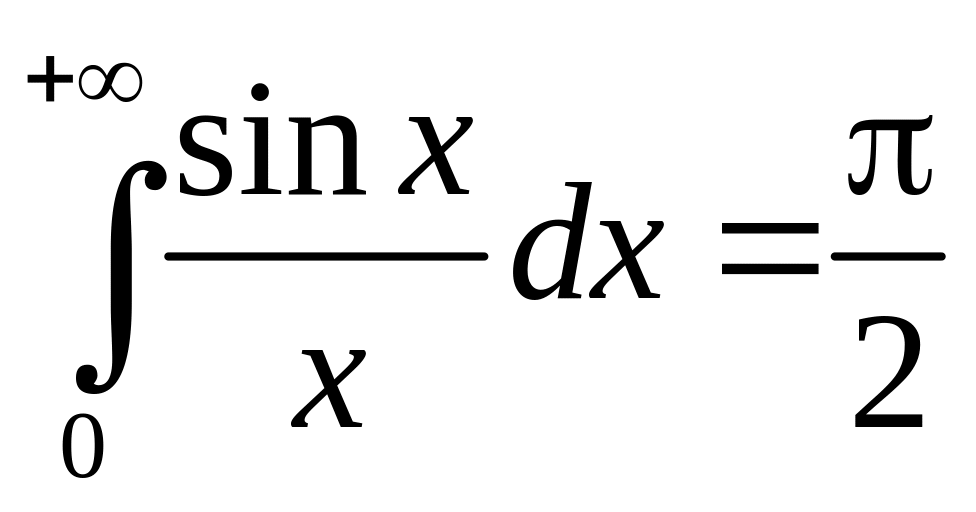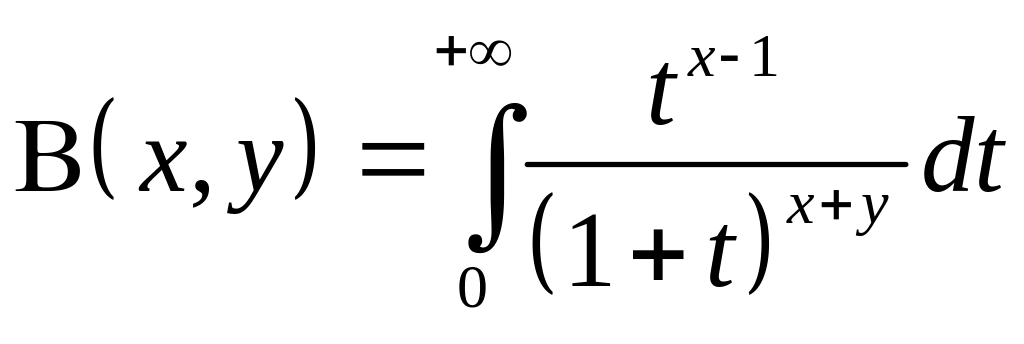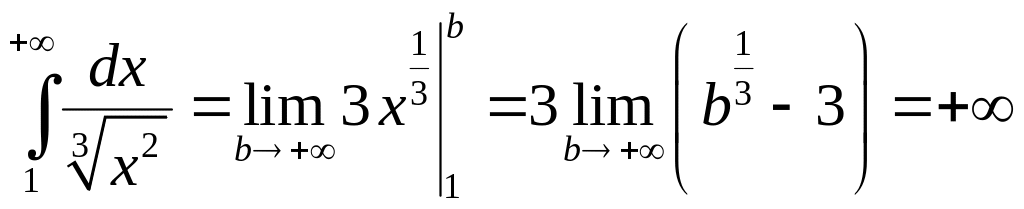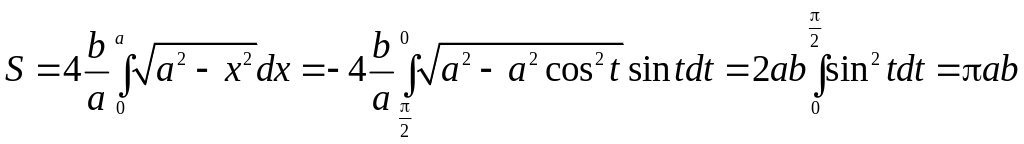Как известно, среднее значение функции f(x), заданной на отрезке [a, b] равно:
Но это только теория, вас же интересует скорее всего практическая сторона, а именно, вам задана какая-то конкретная функция и для неё необходимо найти среднее значение.
Лучше всего рассмотреть как получить среднее значение функции с помощью примера.
Например, вам дана функция:
f(x) = x*sin(x) и надо найти её среднее значение на отрезке [0, π/2]
Для того, чтобы найти ср. значение функции f(x) онлайн, надо воспользоваться тремя двумя шагами:
1. Получить подробное решение определённого интеграла (который стоит в числителе) здесь
Ввести, x*sin(x) как на рисунке ниже:
После этого нажать на кнопку “Найти интеграл”.
Тем самым вы вычислите числитель дроби, который входит в формулу для среднего значения функции.
В нашем примере это значение интеграла будет равно 1, значит числитель будет равен 1.
2. Вычисляем знаменатель. Он равен b — a = π/2 — 0 = π/2
3. Делим числитель на знаменатель и получим необходимое нам среднее значение функции:
22. Оценка интеграла. Теорема о среднем. Среднее значение функции
I. ОцеНКа интеграла. Укажем граНИцы, между которыми наверняка заключено значение интеграла.
Теорема VI (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т. Е.
Где Т и М — Соответственно наименьшее и наибольшее значения функции 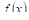
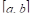
Доказательство. Возьмем две функции 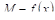
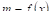
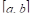
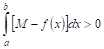
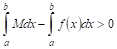
Откуда в силу того, что
Что и требовалось доказать.
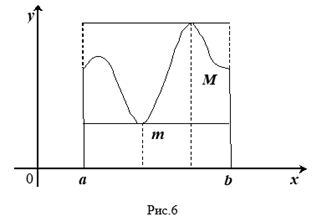
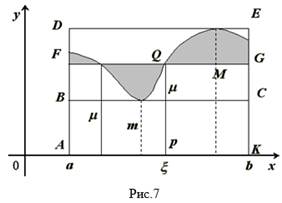
Геометрический смысл этих неравенств таков: площадь КриволиНейной трапеции больше площади прямоугольника с основанием, РавНой оснОваНИЮ трапеции, и высотой, равной наименьшей ординате ТрапециИ, и меньше площади прямоугольника с тем же основанием и Высотой, равной наибольшей ординате Трапеции (рис. 6).
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или дажЕ невозможно найти точное значение Интеграла, а оценивая его, мы узнаем, ХотЯ бы грубо, приближенное его Значение. С такого, рода оценками приходится Довольно часто встречаться в математике.
УказаННые в теореме VI границы для Интеграла тем более точны, чем короче Интервал интегрирования и чем меньше линия 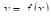
Пример. Оценим интеграл
Легко проверить, что подынтегральная функция в интервале 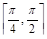
Т. е.
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он равен 0,62.
II. Обобщение теоремы об оценке интеграла. Интегрирование неравенств.
Справедлива следующая более общая теорема, чем теорема VI:
Теорема VII. Если в каждой точке Х интервала
То
Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, Неравенства можно интегрировать..
На доказательстве и геометрическом смысле теоремы останавливаться не будем, так как они вполне подобны предыдущим.
В частном случае, когда 
III. Теорема о среднем.
Определенный интеграл обладает следующим важным свойством:
Теорема VIII (о среднем). Внутри интервала интегрирования 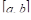
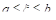
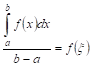
Доказательство. В силу теоремы VI имеем:
Где M — некоторое число, заключенное между наименьшим (Т) и наибольшим (М) значениями функции 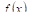
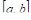
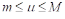
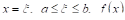
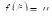
Из равенства (*) находим:
Эта формула позволяет теорему о среднем высказать в такой форме:
ОпредЕЛенный интеграл от непрерывной функции, равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования, на длину интервала.
Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси Ох (рис. 6), вверх от положения ВС площадь прямоугольника АВСК будет непрерывно возрастать от величины, меньшей площади трапеции, до величины, большей ее. Очевидно, при некотором промежуточном положении прямой — обозначим его через FG — Площадь прямоугольника AFGK окажется в точности равной площади трапеции S. Так как при ЭТом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении FG найдется одна или несколько (на рис.
Точек пересечения Q; абсцисса любой точки пересечения и будет требуемым по теореме значением X.
Если трапецию ограничивает прямая линия, то 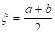
IV. Среднее арифметическое значение функции. Значение 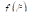
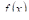
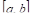
Определение. Средним арифметическИМ значением 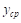
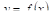
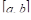
Приведем некоторые соображения в обоснование этого определения.
Пусть некоторая величина У принимает П значений: 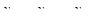
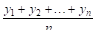
Но представим себе теперь, что величина изменяется непрерывно (например, температура воздуха известна в любой момент суток) и мы хотим как-то в среднем охарактеризовать всю совокупность ее значений. Как в этом случае следует определить среднюю температуру воздуха, принимая во внимание всю известную совокупность знАЧений температуры? Вообще, ЧтО следует принять в качестве среднего значения неПРерывной фуНКции 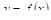
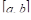
Разобьем интервал 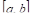
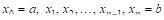
Значениями нашей функции во всех остальных точках интервала пока пренебрежем. Возьмем среднее арифметическое 
Ясно, что чем больше П, тем больше значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение 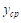
Умножив и разделив выражение для 
Но так как 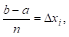
ОТкуда, переходя к пределу, получаем указанное нами выше выражение для среднего значения:
На основании теоремы о среднем (теорема VIII) мы заключаем, ЧТо 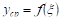
Понятие среднего значения функции очень употребительно в техНИке. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, сила и напряжение переменного тока, скорость химической реакции и т. п.
Среднее значение функции на отрезке
Здравствуйте!
Как найти среднее значение функции на отрезке? Может формулы есть?
Спасибо!
Рассмотрим вопрос о том, как находить среднее значение функции на отрезке.
По этому поводу существует теорема, которая называется теоремой о среднем. В ней говорится, что если на определенном отрезке заданная функция непрерывна, то на этом промежутке найдется такая точка, для которой будет выполняться условие:
Здесь a и b — концы отрезка, f(x) — заданная функция, а с — выше упоминаемая точка.
Значение функции в точке с называют средним ее значением на отрезке от а до b и находят по формуле:
Формулой очень удобно пользоваться, если функция на отрезке задана не линейная, а квадратичная, логарифмическая, тригонометрическая или какая-либо еще.
Рассмотрим пример.
Задание.
Найти среднее значение функции на отрезке [2; 13].
Решение.
Воспользуемся выше упомянутой формулой и подставим в нее известные значения:
Используем формулу Ньютона-Лейбница и найдем значение полученного выражения:
Упростим выражение и вычислим его результат:
Получили среднее значение функции на отрезке [2; 13] равным 35,8.
Пусть
интегрируема и ограничена на
и
,
— соответственно, верхняя и нижняя
грани
на отрезке
.
Тогда, существует такое число
,
что:
и
.
Число
называется средним значением функции
на отрезке
.
Примеры:
4.1. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
4.2. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
4.3. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
5. Несобственные интегралы
5. 1. Интегралы с бесконечными пределами
Если
непрерывна на интервале
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
при
,
то при
интеграл сходится, при
интеграл расходится.
Отметим важные
примеры несобственных интегралов:
– интеграл Пуассона,
– интеграл Дирихле,
– Бета-функция
(эйлеров интеграл 1 рода),
– Гамма-функция
(эйлеров интеграл 2 рода).
Примеры:
5.1.1. Вычислить
интеграл
Найдём
.
Предел существует
и конечен. Значит, интеграл сходится. ◄
5.1.2. Вычислить
интеграл
Найдём
.
Предел не существует.
Несобственный интеграл расходится. ◄
5.1.3. Вычислить
интеграл
.
Подынтегральная
функция чётная, поэтому
.
Вычислим интеграл:
.
Получили
.
Интеграл сходится. ◄
5.1.4. Доказать
расходимость интеграла
.
Так как при
,
,
то вычисляя
интеграл
.
Этот интеграл
расходится. Следовательно, по признаку
сравнения исходный интеграл
тоже расходится.
5.2. Интегралы от функций с бесконечными разрывами
Если
непрерывна на
и неограниченна в любой окрестности
точки
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
при
,
то при
интеграл сходится, при
интеграл расходится.
Примеры:
5.2.1. Исследовать
на сходимость интеграл
.
Так как
подынтегральная функция
терпит
разрыв в точке
,
то получим:
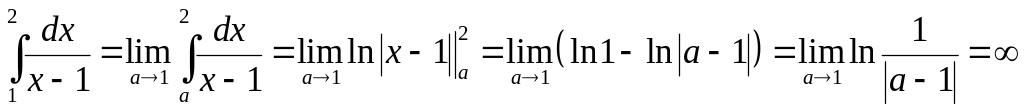
Конечного предела
не существует, значит, интеграл расходится.
◄
5.2.2.
Исследовать на сходимость интеграл
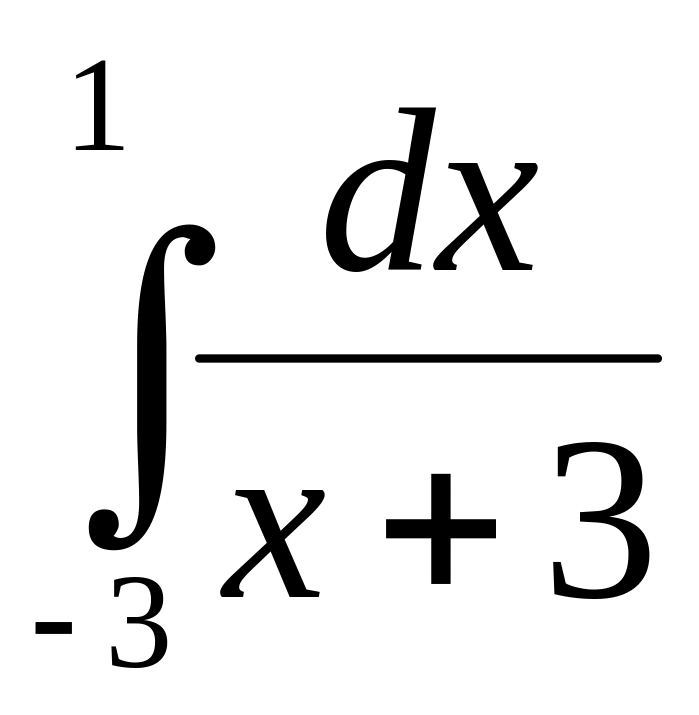
Так как
подынтегральная функция
терпит
разрыв в точке
,
то получим:
.
Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄
5.2.3. Исследовать
на сходимость интеграл

Так как
подынтегральная функция
терпит
разрыв в точке
,
получим:
.
Применим
интегрирование по частям. Пусть
Тогда
.
И первоначальный
интеграл примет вид:
.
Предел конечен.
Поэтому интеграл сходится.
◄
5.2.4. Исследовать
на сходимость интеграл
Имеем
.
Предел бесконечен.
Следовательно, интеграл расходится.
◄
6. Геометрические и физические приложения определенного интеграла
6.1. Вычисление площади криволинейной трапеции
Площадь плоской
области
стандартной относительно оси
,
ограниченной прямыми
и
и кривыми
,
такими, что для любых
выполнено
(т.е.
)
вычисляется
.
Аналогично площадь
плоской области стандартной относительно
оси
,
ограниченной прямыми
и
и кривыми
,
такими, что для любых
выполнено
(т.е.
)
вычисляется
.
Если область
ограничена непрерывной замкнутой
кривой, заданной параметрически
,
то её площадь можно
вычислить по одной из трёх формул
,
,
.
Какую из них удобнее
применять, зависит от конкретного вида
функций
и
.
Площадь области
:
,
называемой
криволинейным сектором, ограниченной
графиком
и двумя лучами, составляющими с полярной
осью углы
и
имеет площадь
.
Примеры:
6.1.1.
Вычислить площадь области, ограниченной
линиями:
и
.
Изобразим фигуру
в декартовой системе координат:
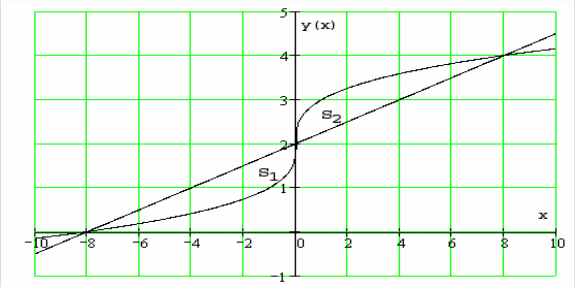
Из условия симметрии
фигуры относительно точки с координатами
,
площади
и
равны. Так как данная область является
стандартной как относительно оси
так и относительно оси
,
то ее площадь можно вычислить одним из
двух способов.
1) Выразим зависимости
в явном виде:
и
,
а стандартная
относительно оси
область
.
Тогда получаем
.
2) Заметим, что для
вычисления площади можно было
воспользоваться исходным видом
зависимостей:
.
6.1.2.
Вычислить площадь области, ограниченной
параболами
и
.
Изобразим фигуру
в декартовой системе координат

Очевидно, область
симметрична относительно оси
,
кроме того, она не является стандартной
относительно оси
и стандартной относительно оси
,
а ее площадь можно вычислить одним из
двух способов.
-
Данная область
не является стандартной относительно
оси.
Её можно разбить на две стандартные
относительно осиобласти:
,
.
Из симметрии
областей
и
относительно оси
следует, что

.
-
Относительно оси
данная область
является стандартной:
.
Снова, используя
симметрию области, получаем
.
6.1.3.
Вычислить площадь эллипса, заданного
уравнением
(
,
).
Искомую площадь
можно вычислить, используя как явное
представление линии, так и параметрическое.
-
Выразив уравнение
в явном виде
,
получим,
применив подстановку
,
,
приходим к
.
2) С другой стороны,
используя параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:
.
6.1.4.
Вычислить площадь астроиды, заданной
уравнением
(
,
)
Изобразим кривую
в декартовых координатах:

Используя
параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:

.
6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой
,
.
Изобразим кривую
в декартовых координатах:
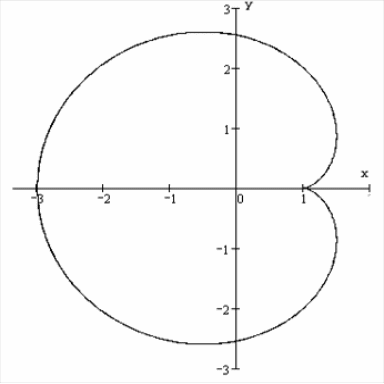
Так как кардиоида
симметрична относительно оси
,
то, используя параметрическое
представление, будем менять параметр
в пределах от
до
.
Так как
и
,
получаем по любой
из трех формул


,


,

.
Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах
равна
.
6.1.6.
Найти площадь области, ограниченной
кривой
.
Кривая образует
три симметричные петли, каждая из которых
ограничивает криволинейный сектор.
Изобразим ее в полярных координатах.

Рассмотрим сектор,
лежащий в первой четверти:
.
Площадь его,
очевидно, равна 1/3 площади всей области,
ограниченной данной кривой. Следовательно,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
среднее:значение:функции:x,:0,:1
-
среднее:значение:функции:x^{frac{2}{3}},:0,:1
-
среднее:значение:функции:sqrt{1-x^{2}}
-
среднее:значение:функции:y=x^{3}
- Показать больше
Описание
Найдите среднее значение функции между интервалами шаг за шагом
function-average-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice Makes Perfect
Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 июня 2019 года; проверки требует 1 правка.
У этого термина существуют и другие значения, см. среднее значение.
Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о среднем значении функции в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



В частности, если 
Вследствие этого под средним значением функции 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
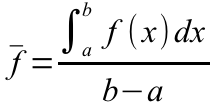

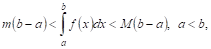
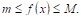

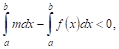
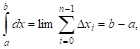
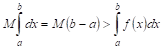
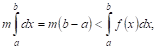
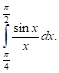
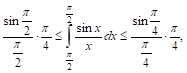
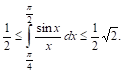
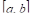
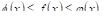
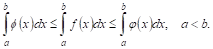
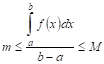
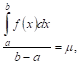
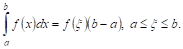
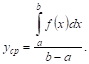
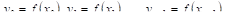
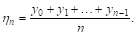
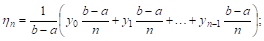
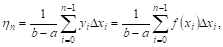
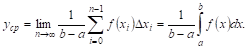
![[fleft(cright)=frac{int^{13}_2{left(x^2-5x+7right)dx}}{13-2}=frac{1}{11}int^{13}_2{left(x^2-5x+7right)dx}=]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f5fb06d35a43a5e42e3d37e18fa0eea9_l3.png)
![[=frac{1}{11}{left.left(frac{x^3}{3}-5frac{x^2}{2}+7xright)right|}^{13}_2=]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ea36ed2767abd91b701c9f1fb39bfb2c_l3.png)