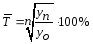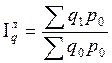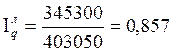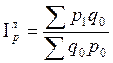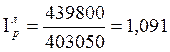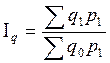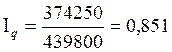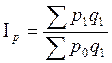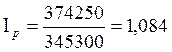На основании данных о посевной площади урожайности озимой ржи по хозяйству определите среднюю урожайность озимой ржи по хозяйству для каждого года.
Данные о посевной площади и урожайности озимой ржи по хозяйству.
| Отделение | 2006 г. | 2007 г. | ||
|---|---|---|---|---|
| Урожайность, ц/га | Посевная площадь, га | Урожайность, ц/га | Валовой сбор, ц | |
| 1-е | 18,5 | 380 | 21,3 | 8520 |
| 2-е | 20,2 | 520 | 23,5 | 11750 |
| 3-е | 23,7 | 600 | 24,4 | 14640 |
Решение:
Для вычисления средней урожайности озимой ржи в 2006 г. воспользуемся формулой средней арифметической взвешенной:
Взвешенная средняя арифметическая — равна отношению суммы произведений значения признака к частоте повторения данного признака к сумме частот всех признаков. Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
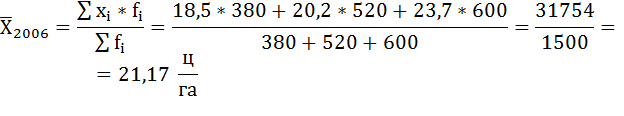
Вывод: Средняя урожайность озимой ржи в 2006 г. составила 21,17 ц/га.
Для вычисления средней урожайности озимой ржи в 2007 г. воспользуемся формулой средней гармонической взвешенной:
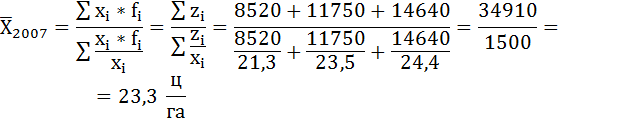
Вывод: Средняя урожайность озимой ржи в 2007 г. составила 23,3 ц/га.
Условие задачи взято из практикума: Общая теория статистики: практикум / С.А. Клещёва. – Пинск: ПолеcГУ, 2009. – 114 с.
Автор решения: Роман Гриб
Цель
занятия:
Освоить
оценку определения урожая и урожайности,
их изменение, изучить факторы, обусловившие
различия в урожайности, выяснить
неиспользованные ресурсы повышения
урожайности, оценить эффективность
различных факторов, влияющих на
урожайность, ознакомиться с источниками
данных об урожае и урожайности; изучить
размер агротехнических мероприятий,
их эффективность, степень распространенности
передовых агротехнических приемов.
Решение
типовых задач
1. Статистика урожая и урожайности
Задача
1.
Предположим
по пяти хозяйствам имеются данные об
урожайности зерновых и валовом сборе:
Таблица
24
Исходные
данные
|
Хозяйства |
Урожайность |
Валовой |
|
1 |
18 |
18000 |
|
2 |
20 |
30000 |
|
3 |
21 |
63000 |
|
4 |
22 |
44000 |
|
5 |
25 |
30000 |
|
Σ |
– |
185000 |
Нужно
рассчитать среднюю урожайность для
всех хозяйств.
Решение:
Для решения задачи следует валовой сбор
всех хозяйств разделить на общую посевную
площадь. Площадь по каждому хозяйству
неизвестна, но легко может быть рассчитана
путем деления валового сбора на
урожайность. Произведя последовательно
все расчеты, получим среднюю урожайность:
 =
= =
=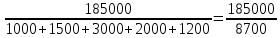 =21,26
=21,26
ц с/га
Если
урожайность обозначить через у1
, а валовой
сбор через W=УП,нетрудно
убедиться, что расчет средней урожайности
произведен по средней гармонической
взвешенной:

Если
бы валовой сбор был везде одинаков, то
значения весов в числителе и знаменателе
сократились бы и можно было бы
воспользоваться средней гармонической
простой:

Задача
2.
Имеются
следующие данные об урожайности и
посевной площади зерновых на двух
участках:
Таблица
25
Исходные
данные
|
№ участка |
Урожайность |
Посевная |
|
1 |
20 |
100 |
|
2 |
30 |
150 |
|
ИТОГО |
х |
250 |
Определите
среднюю урожайность зерновых культур
по двум участком.
Решение.
Определим
среднюю урожайность зерновых культур
по двум участкам по формуле средней
арифметической взвешенной:

Задача
3.
Пусть
имеются следующие данные о производстве
зерна в одном из хозяйств за 5 лет:
Таблица
26
|
Год |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Производство |
50 |
54 |
62 |
70 |
80 |
Рассчитайте:
-
средний
уровень за 5 лет; -
ежегодные
абсолютные приросты; -
ежегодные
темпы роста; -
среднегодовой
темп роста за 4 года.
Решение.
1.
Так как это
интервальный ряд, то средний уровень
ряда (среднегодовое производство зерна)
определим как среднюю арифметическую
простую:
![]()
2.
Ежегодные
абсолютные приросты находим как разность
между двумя уровнями:
для
2007 г……………..54-50=4 тыс.ц.
для 2008 г……………..62-54=8
тыс.ц.
для
2009 г…………..…70-62=8 тыс.ц.
для
2010, г………..……80-70=10 тыс.ц.
3.
Ежегодные коэффициенты роста находим
как отношение уровня каждого года к
предыдущему:
для
2007 г.
![]()
для
2008 г.
![]()
для
2009 г.
![]()
для
2010, г.
![]()
Умножая
коэффициенты на 100%, получаем темпы роста
4.
Среднегодовой
темп роста можно рассчитать как среднюю
геометрическую из годовых темпов роста
которая
тождественна первой
По
первой формуле

По
второй формуле:
![]()
т.е.
среднегодовой темп роста за 5 лет (с 2006
по 2010 г.) равен 112,5%.
Задача
4.
Определите
показатели ряда динамики урожайности
с.-х. культур в хозяйствах всех категорий
Чувашской Республики.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение средней урожайности зерновых с/х предприятий. Расчет сводных индексов цен, физического объема реализации и товарооборота
Страницы работы
Фрагмент текста работы
Задача 1. На основании следующих данных по двум с/х
предприятиям определите насколько и в каком из них средняя урожайность зерновых
выше.
|
Культура |
Предприятие 1 |
Предприятие 2 |
||
|
Валовой сбор, ц |
Урожайность, ц/га |
Посевная площадь, га |
Урожайность, ц/га |
|
|
xf |
x |
f |
x |
|
|
Пшеница |
32000 |
26 |
1580 |
20 |
|
Рожь |
1600 |
19 |
130 |
19 |
|
Ячмень |
13750 |
20 |
660 |
18 |
|
Просо |
1750 |
13 |
120 |
13 |
|
Итого |
49100 |
– |
2490 |
– |
Найдем среднюю урожайность по каждому предприятию с
применением средней арифметической взвешенной. Взвешенная средняя учитывает
различное значение отдельных вариантов в пределах совокупности и применяется,
когда варианты имеют различную численность.
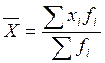
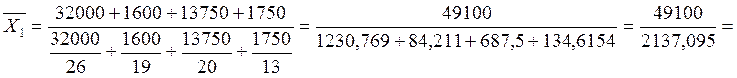
![]() ц/га
ц/га
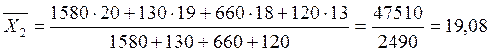 ц/га
ц/га
![]() ц/га
ц/га
Таким образом, на предприятии 1 средняя
урожайность зерновых выше на 3,895 ц/га.
Задача 2.
По данным таблицы найдите:
·
Моду и медиану, используя частоты
и частости;
·
Дисперсию и среднее квадратичное
отклонение, коэффициент вариации.
|
Размер Прибыли млрд.руб. |
3,7-4,6 |
4,6-5,5 |
5,5-6,4 |
6,4-7,3 |
7,3-8,1 |
Итого |
|
Число банков |
2 |
5 |
9 |
4 |
2 |
22 |
Решение
Мода – это
чаще всего встречающийся вариант.
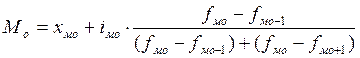 , где
, где
хмо – нижняя граница модального интервала,
iмо – величина модального интервала,
fмо,fмо-1,fмо+1 – частота модального, домодального и послемодального
интервала
Медианой в статистике называется вариант, делящий численность
упорядоченного вариационного ряда на две равные части. Медиана ряда наблюдений
может быть очень далека от типичной величины. Медиана имеет особое свойство –
сумма отклонений членов ряда от медианы есть величина наименьшая.
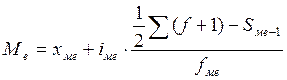 , где
, где
хме – нижняя граница медианного интервала,
iмо – величина медианного интервала,
Sме-1
– сумма накопленных частот в
домодальном интервале.
Для
удобства часть вычислений занесём в таблицу:
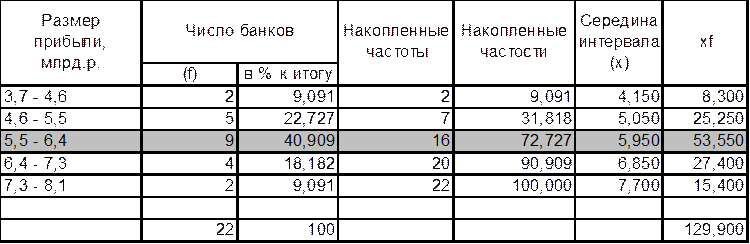
Сначала вычислим моду и медиану через частоты:
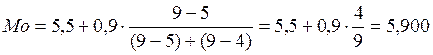 млрд.руб.,
млрд.руб.,
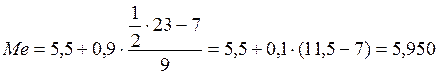 млрд.руб.
млрд.руб.![]()
Теперь вычислим значения моды и медианы через
частости:
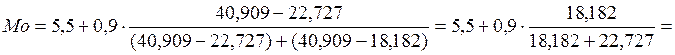
![]() млрд.руб.,
млрд.руб.,
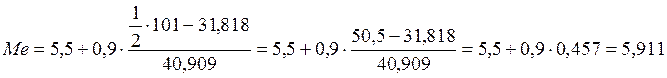 млрд.руб.
млрд.руб.
Вычислим среднее
арифметическое взвешенное:
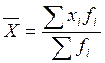 ,
,
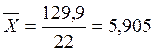 млрд.руб.
млрд.руб.
|
5,911 |
> |
5,905 |
> |
5,900 |
|
Ме |
|
Мо |
||
Можно сказать, что средняя
арифметическая взвешенная, медиана и мода практически совпадают. В этом случае
говорят, что данная группа симметрична.
Вариация – это различие в значениях какого-либо признака у
разных единиц одной совокупности в один и тот же период или момент времени.
Степень колеблемости отдельных значений признака от средней отражают следующие
обобщающие показатели: дисперсия, среднее квадратическое отклонение и
коэффициент вариации.
Дисперсия – средняя арифметическая
квадратов отклонений отдельных значений признака от их средней арифметической.
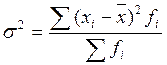 .
.
Среднее квадратическое отклонение (![]() )
)
– корень квадратный из дисперсии. Это абсолютная мера вариации признака в
совокупности.
Для сравнения величины вариации различных признаков и
также для сравнения степени вариации одноименных признаков в нескольких
совокупностях исчисляется относительный показатель вариации – коэффициент
вариации. По величине этого коэффициента можно судить о степени вариации
признаков. Чем больше величина коэффициента вариации, тем больше разброс
значений признака вокруг средней, и тем исследуемая совокупность по своему
составу менее однородна.
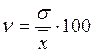 .
.
![]() Опять занесем часть вычислений в таблицу:
Опять занесем часть вычислений в таблицу:
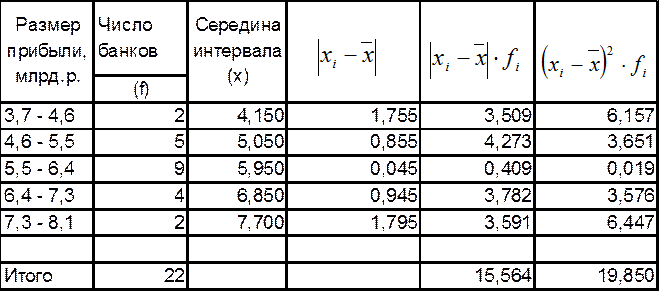
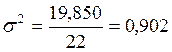 ,
,
![]() млрд.руб,
млрд.руб,
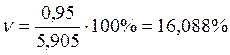 .
.
16,088
% < 30 % , значит совокупность однородна.
Ответ:
Мо = 5,9 млрд.руб., Ме = 5,911 млрд.руб., ![]() = 0,902,
= 0,902,
![]() = 0,95 млрд.руб.,
= 0,95 млрд.руб., ![]() = 16,088%.
= 16,088%.
Задача 3.
По
данным таблицы рассчитайте сводные индексы цен, физического объема реализации и
товарооборота, а также величину перерасхода покупателей от роста цен.
Решение.
Занесем
часть промежуточных вычислений в таблицу:
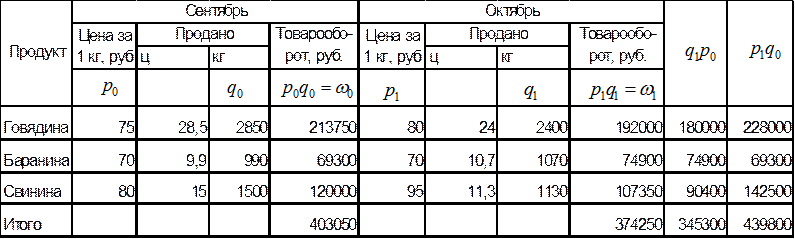
Рассчитаем
сводные индексы по двум видам формул:
1.
По формулам Ласпейреса.
|
Индекс физического объема |
Индекс цены |
|
|
|
2.
По формулам Паше.
|
Индекс физического объема |
Индекс цены |
|
|
|
Теперь найдем индекс
товарооборота:
![]() ,
, ![]()
или
![]() ,
, ![]() .
.
Таким образом, произошло уменьшение товарооборота на
7,1% в связи с увеличением цены на 8,4 % и уменьшением физического объема
реализации на 14,9%. Показатели ухудшились из-за уменьшения физического объема
реализации. Найдем величину перерасхода покупателей от роста цен.
![]() ,
,
![]() млрд.руб.
млрд.руб.
Ответ: сводный индекс цен – 1,084, сводный индекс
физического объема реализации – 0,851, сводный индекс
товарооборота – 0,929, величина
перерасхода покупателей от роста цен – 28950 млрд. руб.
Задача 4
Имеются
следующие данные о производстве электроэнергии в регионе за 1996-2000 гг.
(млрд. кВт/ч):
|
1996 |
1997 |
1998 |
1999 |
2000 |
|
975 |
1038 |
1100 |
1150 |
1220 |
Для анализа ряда динамики
определите:
1.
цепные и базисные:
·
абсолютные приросты;
·
темпы роста;
·
темпы прироста;
2.
абсолютное значение прироста;
3.
средний уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста, среднегодовой темп
прироста.
Решение.
Ряд динамики представляет собой ряд расположенных в
хронологической последовательности числовых значений показателя, показывающих
изменение явлений во времени.
Для анализа рядов динамики применяются следующие
показатели: абсолютный прирост, темп роста, темп прироста, абсолютное значение
одного процента прироста.
Показатели ряда динамики могут вычисляться как на
постоянной, так и на переменной базах сравнения. Сравниваемый уровень
называется отчетным, а уровень, с которым производится сравнение – базисным.
При расчете показателей ряда динамики на постоянной базе сравнения в качестве
Похожие материалы
- Определение типа слушателя и описание средств для привлечения его внимания
- Определение линейной зависимости между выпуском продукции и численностью работающих
- Статистика труда и заработной платы. Методология расчета и анализа трудовых показателей, применяемая в практике экономико-статистических органов
Информация о работе
Как посчитать урожайность сельхозкультуры? Любой хороший финансовый директор должен знать правильный подход к методам подсчета средней урожайности ц га.
Этот расчет используется для того, чтобы получить кредит под залог будущего урожая, для страхования урожая и для прочих расчетов. Особенно часто требуется провести расчет средней урожайности за последние 5 лет. Во всех случаях используются данные формы статистической отчетности 29-СХ и в некоторых случаях формы 4-СХ.
На практике можно встретить 2 способа расчета средней урожайности.
Первый способ, как посчитать урожайность не такой точный, как второй. Итак:
- Значение фактической урожайности берется из 9 столбца формы 29-СХ за каждый год и далее по ним высчитывается простая среднеарифметическая величина.
В нашем случае:
22,6+20,1+9,2+24,4+20,9)/5=19,4.
- Значение фактического сбора урожая берется из 7 столбца, если продукция проходит доработку и 6 столбца, если не проходит. Посевная площадь берется из 4 столбца. Далее складывается валовый сбор за пять лет и складываются площади. Поделив валовый сбор на площадь, получим среднюю урожайность:
(9040+10050+4140+13420+12540)/(400+500+450+550+600)=19,7
Как правильно и точно посчитать урожайность ответы как сделать
Нужно отметить, что второй способ расчета средней урожайности является более точным и более правильным. Для более правильного расчета средней урожайности часто размер посевной площади берут из формы 4-СХ, так как в этой форме отражается изначально посеянная площадь, а в форме 29-СХ в 4-м столбце показывается уточненная посевная площадь. Если, например, часть урожая погибло при перезимовке, то площадь в форме 29-СХ будет меньше, чем в 4-СХ.
Расчет средней урожайности можно проводить просто для анализа урожайности в сельхозпредприятии, также он используется для получения кредита под залог будущего урожая и страхования урожая сельхозкультур.
ВАЖНО ЗНАТЬ!!! Помните, если вы передаете в залог, будущий урожай обязательно уточняйте у кредитного инспектора банка способ расчета средней урожайности.
Задача №1
По приведенным данным исчислите среднюю урожайность зерновых с одного гектара за отчетный год и на предстоящий год:
БригадаОтчетный годПрогноз на предстоящий год
Урожайность, ц с гаВаловой сбор, цУрожайность, ц с гаПосевная площадь, га
1-я22264023130
2-я24240025120
3-я21315023140
Дайте обоснование применению формул средних для расчета показателей.
Задача №11
Рабочий № п/пЭлектровооруженность труда одного рабочего, кВт/ч.Выработка продукции на одного рабочего, тыс. руб.Рабочий № п/пЭлектровооруженность труда одного рабочего, кВт/ч.Выработка продукции на одного рабочего, тыс. руб.
А12А12
16,77,51119,412,4
25,07,0128,78,1
36,08,4135,37,0
410,012,0144,16,5
58,39,5157,89,0
616,38,0164,66,1
А12А12
76,98,51715,616,8
812,014,5187,98,7
93,44,4193,96,9
107,09,3205,87,9
Для изучения зависимости между электровооруженностью труда и выработкой продукции сгруппируйте рабочих по электровооруженности труда, образовав 4 группы с равными интервалами. По каждой группе и в целом по совокупности рабочих подсчитайте:
1) число работников;
2) среднюю электровооруженность труда рабочих;
3) среднюю выработку продукции на одного рабочего.
Результаты группировки оформите таблице. Определите эмпирическое корреляционное отношение. Сделайте выводы.
Задача № 17
Имеются данные о ценах и количестве поданных товаров:
Вид товараЕдиница измеренияЦена за единицу, руб.Реализовано, тыс. ед.
Предыдущий периодОтчетный периодПредыдущий периодОтчетный период
Мясокг80110600500
Молокол1525800900
Определите:
1)общий индекс цен;
2) общий индекс физического объема товарооборота;
3) общий индекс товарооборота.
Сделайте выводы и покажите взаимосвязь индексов.
Задача № 34
Потребительские цены РФ в 2000 г. по сравнению с декабрем 1999 г. изменялись следующим образом:
МесяцНепродовольственные товарыПродовольственные товары Платные услуги населению
Январь102,2102,2103,4
Февраль103,5102,6106,4
Март105,0102,7108,0
Апрель106,5103,0110,3
Май107,7105,3111,8
Июнь108,6108,7115,2
Июль109,5110,6119,5
Август111,0110,9123,1
Сентябрь113,3111,6126,5
Октябрь115,4114,0129,5
Ноябрь117,1115,7131,6
Декабрь118,5117,9133,7
По данным, характеризующим групповые индексы цен, определите:
1) в каком полугодии инфляция была выше и по какой группе товаров и услуг цены росли быстрее;
2) какой месяц II полугодия выделяется максимальным ростом цен.
Ну хотябы одну из них, пож-та. а нужно все.Спасиб. Учусь заочно.Незнаю как делать ,чесно слово))