Как найти среднюю величину признака биология

Среднее значение признака и методы вычисления этой величины

Полученные
при обследовании значения признаков
характеризуют каждую конкретную особь
в отдельности. Общие свойства совокупности
оценивают с помощью средней величины,
которую обозначают в биометрии буквой
M или
.
Этот показатель используется для
характеристики однородных групп
животных по какому-либо признаку,
сравнения отдельных стад и пород, оценки
предприятий, хозяйств и конкретных
специалистов. Так, например, если в одном
хозяйстве средний удой на корову
составляет 3000 кг, а в другом – 4000 кг, то
по среднему значению признака видно,
где лучше стадо.

Различают
несколько методов вычисления средней
арифметической величины. Наиболее
простой, который используют в основном
для малых выборок –  метод
суммирования:
складывают все значения вариант и делят
их

сумму
на объем выборки. В математическом
выражении это выглядит так:

  ∑V
где ∑ – знак суммирования,

M
= ─── ; V – значения вариант,

n
n – объем выборки.

Для
примера найдем с помощью этого метода
среднюю живую массу 10 гусей, кг: 5,6
7,0 6,3 7,4 8,0 6,7 6,4 6,9 6,1 6,8

5,6
+ 7,0 + 6,3 + 7,4 + 8,0 + 6,7 + 6,4 + 6,9 + 6,1 + 6,8 67,1

M
= ────────────────────────────────
= ─── = 6,71 кг.

10
10

В
случаях, когда значения признака имеют
разные частоты (вес) или в каждой группе
уже известны средние показатели, среднюю
арифметическую величину определяют
 методом
взвешивания:
каждое значение признака умножают на
его частоту, полученные произведения
суммируют и делят на объем выборки.
Среднюю взвешенную величину вычисляют
по формуле:

p₁V₁
+ p₂V₂
+ p_nV_n
∑рV где М – средняя взвешенная,

M
= ───────────── = ────; p
– частоты,

p₁
+ p₂
+ p_n
  ∑p V – варианты.

Для
примера вычислим этим методом среднюю
жирность молока коровы Зорьки за лактацию
(табл.3).

3.
Продуктивность коровы Зорька по месяцам
лактации

В
этом примере за конкретное значение
признака (V) взят процент жира в молоке
коров, а за частоту (р) – месячный удой.

∑рV
18155

M
= ──── = ──── = 3,65(%)

∑р
4969

При
группировке цифрового материала в
вариационный ряд среднюю арифметическую
величину удобно вычислять  методом
условных отклонений по
формуле:

  ∑рa
где  A – условно среднее
значение

M
= A + i ──── ; i – классовый интервал

n
р – частота, а – условное откл.

n
– объем выборки

Используя
этот метод, вычислим среднюю длину
шерсти овец породы прекос по следующим
данным: (см)

7,5
8,5 8,0 8,0 9,0 10,0 8,5 10,0 7,0 6,0 7,5 9,0
10,0 8,0

9,0
10,0 7,0 9,5 8,5 8,0 10,0 7,5 8,5 9,0 8,0 9,5
8,5 8,0

10,0
12,0 11,0 9,0 8,5 8,0 8,5 9,0 11,0 7,0 9,0 8,5

n
= 40

Для
построения вариационного ряда находим
минимальное и макси-мальное значения
признака, определяем лимит, устанавливаем
число классов и величину классового
промежутка.

1.
min
= 6,0; max
= 12,0; lim
= 12,0 – 6,0 = 6,0

2.
Число классов – 6

lim
6,0

3.
Классовый промежуток i = ──────────
= ─── = 1,0 (см).

число
классов 6

Схема
расчета приведена в таблице 4.

4.
Алгоритм вычисления средней арифметической
величины методом условных отклонений

После
построения вариационного ряда выделяем
условно среднее значение признака – A.
Обычно это среднее значение класса с
максимальной частотой. В нашем примере
A = 8,5. Затем проставляем условные
отклонения (а), которые показывают, на
сколько классовых промежутков каждый
из классов отклоняется от условно
среднего или нулевого класса. Вверх от
нулевого идут отрицательные отклонения,
вниз – положительные. После заполнения
таблицы находим для каждого класса
произведение частот (р) на отклонения
(а) и их сумму ( ∑ра). Теперь по формуле
находим среднее значение признака:

∑рa
22

М
= A
+ i
───── = 8,5 + 1,0 ─── = 9,05 (см)

n
40

Кроме
средней арифметической величины
среднее значение признака характеризуют
средняя геометрическая (G), средняя
квадратическая (S), средняя гармоническая
(H), мода (Мо) и медиана (Ме). Сведения об
этих величинах и их использовании можно
найти в специальной литературе по
биометрии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками. 

Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.

Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.

Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.

Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!

Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г

IV. Тест по русскому языку

1. В тексте про белых медведей больше всего предложений:

а) повествовательных; б) вопросительных

2. Восклицательное предложение находится: 

а) в начале текста; б) в конце текста

3. Вопросительное предложение находится 

а) в начале текста; б) в конце текста

4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются

а) родственными словами; б) однородными членами предложения 

5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:

а) I спряжения; б) II спряжения

6. Эти глаголы стоят в форме:

а) настоящего времени; б) будущего времени; в) прошедшего времени

7. Эти глаголы стоят в форме:

а) единственного числа; б) множественного числа

8. Эти глаголы стоят в форме:

а) 1-го лица;     б) 2-го лица;  в) 3-го лица;    г)нельзя определить лицо

9. Эти глаголы стоят в форме:

а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род

10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:

а) два слова; б) три слова  

11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж: 

а) Р.п.; б) В.п.

На этой странице сайта размещен вопрос Помогите рассчитать среднюю величину выраженности по формуле M = V * P / n, где М – средняя величина , V – размер, P – частота встречаемости 1)Надо подставить вот это : (РАЗМЕР СЕМЕЧКИ)1, 1 (32)(КОЛ -? из категории
Биология с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 10 – 11 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.

Лабораторная работа

Изучение статистических закономерностей модификационной изменчивости

Цель: показать статистические закономерности модификационной изменчивости на примере использования математических методов в биологии. Построить вариационный ряд, график, определить среднюю величину признака.

Оборудование и объекты исследований: семена фасоли, бобы, желуди, плоды клена, каштана, гербарии листьев лавровишни, коллекции раковин, колосья и другие.

Ход работы

I. Теоретическая часть

Организмы наследуют не признак как таковой, а способность формировать определенный фенотип в конкретных условиях среды, т.е. норму реакции.

Норма реакции – ПМИП – пределы модификационной изменчивости признака. Разнообразие фенотипов, возникающих у организмов под влиянием условий среды, называют модификационной изменчивостью.

Модификационная изменчивость – явление массовое, изменения касаются не отдельного организма, а группы. Всю группу объектов, которая подлежит изучению, называют генеральной совокупностью. Часто бывает трудно, а иногда практически невозможно ее исследовать. Поэтому изучают только часть особей – выборочную совокупность, по которой дают общую характеристику (выборочный метод). Выборку необходимо брать из однородного материала без специального подбора, т.е. так, чтобы она отражала генеральную совокупность.

Модификационная изменчивость

Качественная Количественная

количество объектов о опреде- характеризуется разной мерой

ленным качественным признаком, выраженности, признака

обычно выраженным в % от

общего количества

Дискретная (прерывная) Непрерывная

признаки выражены в целых признак, который варьирует, из-

числах,между которыми нет пе- меряется числами, между которыми

реходов (количество листьев на возможны переходы (масса, длина)

растении: количество зерновок в колосе)

Объективную характеристику качественной изменчивости можно дать только при использовании статистических методов исследования: составления вариационных рядов и вычисление их параметров. Отдельные значения признаков, которые варьируют называются вариантами (v). Число, которое обозначает, сколько раз повторяется варианта, называется частотой встречаемости варианты (p). Сумма всех частот равна количеству объектов в ряду и обозначается (n). Основные показатели ряда признака, который варьирует-среднее арифметическое (М) и среднее квадратное отклонение (σ – сигма). Σ, σ

Чем ближе варианта к среднему значению, тем чаще она встречается, т.е. тем больше вероятность ее возникновения. Варианты распределяются по обе стороны от среднего арифметического, как правило, симметрично. Чтобы дать объективную харакитеристику изменчивого признака, нужно изучить большое число особей.

Вариационный ряд – ряд изменчивости данного признака.

Вариацоннная кривая – частота встречаемости отдельных вариант, отражающая изменчивость признака.

II. Практическое исследование

1. Рассмотрите несколько растений одного вида, выделите сравниваемый параметр (длину листьев, ширину листьев, количество простых листьев на сложном листе, число колосков и другие). Сравниваемый параметр _________________________________________________________

2. Постройте вариационный ряд и вариационную кривую. Определите, какие признаки встречаются наиболее часто, а какие редко.

1) Для этого измерьте выбранный параметр для 10-20 объектов.

____________________________________________________________________________________________________________________________________

2) Расположите ваши данные на листе бумаги в порядке нарастания величины данного признака, обозначьте величины признака и проведите линию, соединяющую ваши объекты – получите вариационный ряд.

3) Запишите полученные данные вариационного ряда в таблицу:

3) Постройте вариационную кривую (графическое выражение изменчивости признака). Отобразите на графике зависимость между изменением признака и частотой его встречаемости. По оси абсцисс отложите на определенном расстоянии отдельные варианты признака в нарастающем порядке; по оси ординат отложите числовые значения, соответствующие частоте повторяемости каждой варианты; от горизонтальной оси восстановите перпендикуляры до уровня, соответствующего частоте повторяемости варианты – точки пересечения перпендикуляров с линиями, соответствующими частоте встречаемости вариант, соедините линиями.

3. Определите среднюю величину указанного признака по формуле.

Р – частота встречаемости вариант

V – Варианта, варьирующий признак

Рис. Вариационная кривая

Среднюю величину М находят по формуле M = Σ(V x P)/ n

v – варианта, значение отдельного признака;

p – частота встречаемости определенной варианты

n – общее число исследуемых объектов;

M – средняя арифметическая величина;

m – ошибка средней;

Mo – мода, т.е. наиболее часто встречающаяся варианта;

lim – размах изменчивости (лимит, определяемый нормой реакции)

σ – среднее квадратичное отклонение

Размах изменчивости определяют: из наибольшей величины вычитается значение, предшествующее минимальной

lim = Vmax – Vmin-1

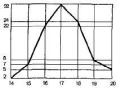
Если же наш результат оказался недостоверным, это значит ошибка m очень большая.
Вспомним, что

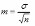
Среднее квадратическое отклонение (синонимы: стандартное отклонение, сигмальное отклонение, сигма) – мера вариабельности вариационного ряда. Является интегральным показателем, объединяющим все случаи отклонения вариант от средней. Фактически, отвечает на вопрос: насколько далеко и как часто варианты распространяются от средней арифметической. Обозначается греческой буквой σ (“сигма”).

При численности совокупности более 30 единиц, стандартное отклонение рассчитывается по следующей формуле:

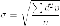
Для малых совокупностей – 30 единиц наблюдения и менее – стандартное отклонение рассчитывается по другой формуле:

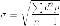
Для этого следует провести лабораторную работу. Взять 15 фасолин.

Измерить длину семени фасоли:

№ измерения
1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Длина
в мм (V)

Определить частоту встречаемости значений длины семени. Определите, какая длина встречается наиболее часто, какая — редко.

Значение длины в мм (V)

Частота встречаемости (Р)

Это вариационный ряд.

Постройте вариационную кривую. Для этого по горизонтали (на оси
абсцисс) отложите размеры семени, по вертикали (на оси ординат) — число,
соответствующее частоте встречаемости. Масштаб может быть произвольный.

Определите норму реакции (используйте для этого задание №2). Норму
реакции вычисляют следующим образом. От максимального размера длины
листьев вычитают минимальный размер. N= max-min

Определите среднюю величину признака по формуле:

M = ∑ (v •р) / n,

где М – средняя величина, V – варианта, P – частота встречаемости вариант, n – общее число вариант вариационного ряда.
Сделайте вывод о том, какая закономерность модификационной изменчивости вами обнаружена.