Как найти среднюю высоту дерева

Лекция
6

Таксационные
показатели насаждений по элементам
леса. Возраст, средний диаметр и высота.
Бонитет насаждений, бонитетные шкалы.
Полнота и сомкнутость насаждений, их
определение и взаимосвязь. Классы
товарности. Типы леса и типы условий
местопроизрастания. Таксация подроста,
подлеска, оценка напочвенного покрова
и почв.

ПЛАН

1.ВОЗРАСТ
ДРЕВОСТОЯ

2.
СРЕДНИЙ ДИАМЕТР И СРЕДНЯЯ ВЫСОТА
ДРЕВОСТОЯ

3.
БОНИТЕТ НАСАЖДЕНИЙ

4.
ТИП ЛЕСА

5.
ПОЛНОТА НАСАЖДЕНИЙ

6.
КЛАСС ТОВАРНОСТИ

Возраст
древостоя является одним из важнейших
таксационных показателей. Все основные
лесохозяйственные мероприятия (рубки
ухода, рубки главного пользования и
др.) назначаются и проводятся с обязательным
учетом возрастных этапов древостоя.

Отдельные
деревья, составляющие любой древостой
(за исключением чистых культур), обычно
различаются по возрасту. Древостой,
следует различать его преобладающему
и среднему возрасту.

Преобладающим
называют возраст, который имеют
большинство деревьев древостоя. Средний
возраст определяется как средневзвешенная
величина отдельных возрастных групп
деревьев (элементов леса) по формуле:

Aср=
(А₁М₁+А₂М₂+А₃М₃+…..+А_nМ_n)/(M₁+M₂+M₃+M_n)

где
A₁,
А₂,…,
А_n
— возрасты отдельных групп или поколений
деревьев, слагающих древостой (ярус),
лет;

M₁,
М₂,…,
М_n—
их запасы, м3.

Например,
в еловом древостое, состоящем из двух
возрастных поколений, 70 % запаса приходится
на 120-летние деревья, а 30 % — на 80-летние.
Средний возраст этого древостоя равен

Aср=(120*70+80*30)/100=108
лет

тогда
как преобладающим возрастом является
120 лет. Чем однороднее древостой, тем
меньше разница между средним и
преобладающим возрастами.

Определение
запаса элемента леса дело сложное и
трудоемкое. Учитывая то, что запасы
составляющих древостой элементов леса
прямо пропорциональны их суммам площадей
сечений (ΣG), приведенную выше формулу
можно записать

А_ср=(А₁*G₁+A₂G₂+……+A_n*G_n)/(G₁+G₂+…….G_n)

где:
G₁,
G₂,…
G_n
–
суммы
площадей сечений отдельных элементов
леса на круговых пробных площадках.

В
чистых простых древостоях его средний
возраст часто определяют как
среднеарифметический возраст отдельных
деревьев, взятых в качестве моделей.
При этом для определения возраста
моделей пользуются возрастным буравом
(растущие деревья), или подсчитывают
число годичных слоев на пнях (срубленные
деревья).

У
молодых деревьев сосны (до 50… 60 лет)
возраст можно определить подсчетом
числа мутовок на стволе. В смешанных и
сложных насаждениях возраст определяется
отдельно для каждого элемента леса.

При
лесоинвентаризации за единицу измерения
возраста принимается не 1 год, а некоторый
период называемый классом
возраста.

Величина
класса возраста для разных пород
установлена в зависимости от
продолжительности их жизни и возраста
рубки. Для хвойных и твердолиственных
древостоев семенного происхождения с
большей долговечностью продолжительность
класса возраста принята равной 20 годам.
Для мягколиственных и твердолиственных
древостоев порослевого происхождения
– 10 годам.

При
массовой таксации в первом случае
возраст древостоя определяется с
градацией 10 лет, во втором – 5 лет. Для
древостоев, состоящих из быстрорастущих
пород (тополя, ивы, акации) с очень низким
возрастом их рубки (до 30…40 лет), класс
возраста принят равным 5 годам. Иногда
для долговечных пород с очень высокими
возрастами рубки (кедр) допускаются
40-летние классы возраста. Классы возраста
обозначаются римскими цифрами.

Древостой
считается одновозрастным, если деревья
имеют разницу в возрасте не превышающую
продолжительность одного класса
возраста. Если разница больше, то такой
древостой относится к разновозрастному.

Древостои
из светолюбивых пород (сосны, лиственницы)
чаще всего одновозрастные, а из
теневыносливых (ели, пихты) – разновозрастные.

Между
морфологическими признаками деревьев
и их возрастом существуют корреляционные
зависимости. Поэтому в практике
лесоинвентаризационных работ средний
возраст древостоев чаще всего определяют
по внешним признакам деревьев:

1. Высоте
   и диаметру с учетом их зависимости от
   условий местопроизрастания,

2. Форме
   кроны,

3. Углу
   ветвления сучьев,

4. Цвету
   и строению коры (ее трещиноватости) и
   т. д.

В
таксационных описаниях каждый древостой
характеризуется классом возраста и
преобладающим возрастом.

В
смешанных и сложных древостоях возраст
определяется по элементам леса. Древостой
в целом относится к тому классу
возраста,
который имеет преобладающий
элемент леса,
например 4С
(160)
ЗС (100) ЗБ (70).

В
разновозрастных
древостоях, где поколения выделить
трудно, указываются нижний
и верхний пределы возраста. Средний
возраст определяется по возрасту
преобладающего числа деревьев, например
10E (110,
80 – 120) .

Для
решения ряда практических задач классы
возраста объединяют в группы
возраста: молодняки,
средневозрастные, приспевающие, спелые
и перестойные. Исходным основанием для
деления насаждений по группам возраста
является принятый возраст рубки.
Распределение насаждений по группам
возраста при возрасте рубки 101… 120 лет
(VI класс) показано в табл.

Распределение
насаждений по группам возраста

Группа возраста	Молодняки	Средневозрастные	Приспе- вающие	Спелые	Перес- тойные
Классы возраста	I	II	III	IV	V	VI	VII	VIII
Возраст, лет	1-20	21-40	41-60	61-80	81-100	101-120	121-140	141- 160

Как
правило, к
молоднякам относятся древостои первых
двух классов возраста; спелыми считаются
древостои, относящиеся к классу возраста
рубки и следующего за ним класса; к
приспевающим
– один класс возраста, предшествующий
спелым; все остальные классы возраста,
которые находятся между молодняками и
приспевающими древостоями, считаются
средне- возрастными.

Для
численной характеристики древостоя
определяют средний диаметр D_cp

и среднюю высоту Н_ср
деревьев. Эти два таксационных показателя
находятся в тесной зависимости. С
увеличением диаметров деревьев
увеличивается и их высота. Эта связь
характеризуется выпуклой кривой.

Способы
определения этих показателей базируются
на закономерностях строения древостоев
по диаметру и высоте и в зависимости от
требуемой точности могут быть различными.
При проведении лесоустройства средний
диаметр и среднюю высоту часто определяют
визуально.

При
отводе и таксации лесосек или работе
на пробных площадях, требующих большей
точности, необходимы специальные
измерения. Например, чтобы определить
средний диаметр нужно иметь перечетную
ведомость, характеризующую распределение
числа стволов в древостое по ступеням
толщины, а для определения средней
высоты – еще и данные измерения высоты
модельных или учетных деревьев.

Средний
диаметр древостоя

D_ср
это средняя толщина древесных стволов
на высоте 1,3 м (высота груди человека
среднего роста) от шейки корня дерева.

Различают
среднеарифметический и среднеквадратический
диаметры. Среднеарифметический диаметр
определяется как частное от деления
суммы диаметров всех деревьев элемента
леса на число деревьев. Среднеквадратический
(таксационный) диаметр
определяется через среднюю площадь
сечения путем деления суммы площадей
сечений деревьев всех ступеней толщины
на общее число деревьев.

g_ср
=
ΣG/N
= πD²_cр/4

D_ср=2*корень(g_ср/π)

Из
всех способов определения среднего
диаметра этот способ является наиболее
точным, так как дерево, имеющее
среднеквадратический диаметр, будет
близким к среднему и по другим таксационным
показателям — высоте и объему.

Между
среднеарифметическим и среднеквадратическим
диаметрами существует зависимость,
согласно которой последний всегда
больше первого.

D_ср.
кв=
корень(D²_{ср.
ариф.}+σ²)

При отсутствии данных перечета деревьев приближенное значение Dср, можно определить по модельным деревьям делением суммы их диаметров или суммы площадей сечений на число моделей. По правилам математической статистики расчет числа моделей n производится по формуле: n=Vd2/P2 где: Vd – коэффициент дифференциации диаметров стволов древостоя элемента леса, %; P – заданная точность определения среднего диаметра, %. Отсюда, для определения среднего диаметра с ошибкой не более ±10 % при коэффициенте дифференциации диаметров 25…30% необходимо измерить 7…9 моделей, отобранных по методу случайной выборки. Для снижения величины варьирования диаметров, а следовательно, и повышения точности установления среднего диаметра модельные деревья можно отбирать из числа близких по диаметру к среднему дереву.

В
лесоустройстве при массовой таксации
лесов средний диаметр определяется с
градацией 2 см (при среднем диаметре
древостоя до 32 см) и 4 см (при большем
среднем диаметре).

В
приспевающих, спелых и перестойных
древостоях средний диаметр устанавливается
раздельно по элементам леса, а в молодняках
и средневозрастных – только для
преобладающей породы.

Для
приближенных расчетов среднего диаметра
рекомендуют способы, основанные на
закономерностях строения насаждений,
согласно которым среднее дерево в
древостое в общем ряду распределения
деревьев по ступеням толщины занимает
строго определенное место. Так в
древостое, состоящем из одного элемента
леса, средний диаметр составляет около
60 % диаметра самого толстого дерева и
примерно в 2…2,3 раза больше диаметра
самого тонкого; около
60
% общего числа деревьев древостоя имеют
диаметр меньше среднего, а 40% больше
его.

Средняя
высота древостоя

Н_ср–
важный
таксационный показатель. В сочетании
с другими показателями (возрастом,
диаметром, полнотой) она служит для
численной характеристики состояния и
производительности как древостоя, так
и качества условий местопроизрастания.

Она является основой построения многих важнейших нормативно-справочных материалов для таксации леса (бонитетных шкал, таблиц стандартных значений сумм площадей сечений и запасов и др.). В зависимости от цели и требуемой точности средняя высота может быть определена разными способами. В лесоустройстве при массовых лесоинвентаризационных работах она определяется чаще всего глазомерно (на основе навыка, приобретенного на тренировочных пробных площадях) с градацией 1 м.

В
качестве придержки при определении Нср
можно использовать закономерность,
согласно которой средняя высота древостоя
элемента леса меньше высоты самого
высокого дерева примерно на 15%, и больше
самого низкого на 20…30%. В молодых
древостоях эти пределы несколько
расширяются.

Для
контроля
точности
глазомерной
таксации
используются данные трех, пяти модельных
деревьев, подобранных на глаз, близких
по размерам к средним по диаметру и
высоте.

На
пробных площадях и при исследовательских
работах Н_ср
определяют более точными методами (до
0,1 м). Для этого измеряют высоты и диаметры
15..25 модельных (учетных) деревьев с
последующим построением графика высот.
Деревья подбирают методом
пропорционально-ступенчатого
представительства.

Рис.
Определение средней высоты насаждения
по кривой высот

Кривая
высот
показывает
изменение средней высоты отдельных
ступеней толщины при переходе от тонких
деревьев к толстым.

Чтобы
определить среднюю высоту по графику,
на оси абсцисс находят место среднего
диаметра. Из этой точки восстанавливают
перпендикуляр до пересечения его с
кривой высот. Значение ординаты точки
пересечения и будет средней высотой
древостоя. Из рисунка видно, что она
равна 26 м.

Для определения среднеарифметической высоты каждой породы методом случайной выборки измеряют высоту 12…15деревьев, отобранных механическим способом. Данные измерений суммируют и делят на число моделей. Исходя из коэффициента варьирования высоты, характеризуемой в среднем для всех пород 8%, ошибка в определении высоты в этом случае не будет превышать + 3 %. С целью уменьшения числа изме- ряемых деревьев до 5…9 рекомендуется подбирать модели только из центральных ступеней толщины, следя за тем, чтобы их высота резко не отличалась от средней высоты для этих ступеней.

Определение
средневзвешенной высоты требует наличия
перечетной ведомости и данных измерений
высот модельных деревьев по ступеням
толщины. Расчет Н_ср
производится по формуле:

Н_ср
=(h₁*g₁+h₂*g₂+h₃*g₃+…….+h_n*g_n)/(g₁+g₂+g₃+…..g_n)

где:

h₁,
h₂,
… h_n—
среднеарифметические высоты модельных
деревьев отдельных ступеней толщины,
м;

g1,
g2, … gn – суммы площадей сечений деревьев
этих ступеней, м².

В
смешанных и сложных насаждениях среднюю
высоту яруса определяют как средневзвешенную
через коэффициенты состава или запасы
составляющих пород.

Пусть
в древостое, имеющем состав 6С4Б, средняя
высота сосны 25, а березы 22 м.
Тогда
средневзвешенная высота яруса равна

Н_ср
=(25*6+22*4)/10=23,8
м

В
последнее время для решения ряда
практических задач определяют верхнюю
высоту. Она
вычисляется как среднеарифметическая
высота 100-150 самых крупных (по высоте и
диаметру, превышающим средние размеры)
деревьев элемента леса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Министерство
образования и науки Челябинской области

Государственное
бюджетное профессиональное образовательное учреждение «Чебаркульский профессиональный
техникум»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

УРОКА

по специальности
35.02.01

«Лесное и лесопарковое хозяйство»

ПМ.04
Проведение работ по лесоустройству и таксации

МДК. 04.01 «Лесная таксация»

Тема: ««Перечислительные и измерительные методы
определения таксационных показателей древостоя (среднего диаметра, высоты)»

Разработал: Митрофанов С.В.,

преподаватель общепрофессиональных

 и специальных дисциплин  

Пояснительная
записка

Внедрение образовательных стандартов третьего
поколения ставит перед нами ряд проблем по выполнению их требований, среди
которых особо актуальной является проблема организации образовательного
процесса в части выбора методов и технологий обучения, обеспечивающих процесс
формирования у обучающихся общих и профессиональных компетенций.

Главной идеей новых стандартов признана идея
непрерывного развития человека как субъекта, образования в течение всей жизни.
Важным становится ориентация образовательной деятельности на преобразование
мира, а не только на его познание, на развитие способностей человека, его
саморазвитие и самообразование. В соответствии с данными задачами интерес
вызывает технология проблемного обучения.

Проблемное обучение — такая форма, в которой процесс
познания обучающихся приближается к поисковой, исследовательской деятельности.
Успешность проблемного обучения обеспечивается совместными усилиями
преподавателя и обучающегося. Основная задача педагога — не столько передать
информацию, сколько приобщить обучающегося к объективным противоречиям развития
научного знания и способам их разрешения. В сотрудничестве с преподавателем
обучающиеся «открывают» для себя новые знания, постигают, расширяют свои
познания отдельной науки.

В данной  методической разработке, в контексте
заявленной темы, представлен   пример практического использования указанной
технологии на уроке междисциплинарного курса МДК 04.01 Лесная таксация в рамках
профессионального модуля ПМ.01 Проведение работ по лесоустройству и таксации

.

План урока

Раздел программы: Техника, методы, учёт и
оценка лесных ресурсов

Тема раздела программы: Таксация лесных насаждений

Тема урока: Перечислительные и измерительные
методы определения таксационных показателей древостоя (среднего диаметра, средней
высоты)

Цели:

Обучающие:

– систематизировать знания обучающихся о таксационных
показателях, используемых в лесной таксации;

– ознакомить обучающихся со способами определения
таксационных показателей насаждений (среднего диаметра, средней высоты).

Развивающие:

– развивать у обучающихся интерес к спецдисциплине;

– развивать логическое мышление обучающихся;

– развивать зрительную память и наблюдательность.

Воспитательные:

– воспитание у обучающихся любви и чувства значимости
к выбранной профессии.

Тип урока: усвоение новых знаний.

Вид урока: урок-беседа.

Методы
обучения: частично-поисковый, наглядный, беседа

Оснащение: Рабочая тетрадь, компьютер,
мультимедийный проектор, экран, презентация, разработанная преподавателем,
калькулятор

Методическая литература:

1.  В.В. Загреев. «Лесная таксация и Лесоустройство» М.
«Экология», 1991 г.

2. Ф.И. Семенюта. «Лесная таксация и лесоустройство».
М. «Лесная промышленность», 1984

3. А.Н. Поляков.  «Практикум по Лесной таксации». М.,
ФСЛХ РФ, 1998 год

Этапы 
урока

Этап	Деятельность преподавателя	Деятельность обучающихся
Организационный момент	Приветствие Активизация познавательного интереса Сообщение темы и целевая установка на урок.	Приветствие Психологический настрой
Актуализация опорных  знаний	Мотивирует на повторение;  задает вопросы, корректирует ответы	Отвечают на вопросы
Изучение нового материала	Постановка проблем; объяснение нового материала, опираясь на презентацию	Делают пометки в конспектах
Формирование выводов по  изученному материалу (организация дискуссии)	Отвечают на вопросы
Выполнение самостоятельной работы	Разбивка на варианты Проведение расчетов по вариантам
Закрепление изученного материала	Задает вопросы	Отвечают на вопросы
Выдача домашнего задания	Объясняет как выполнить задание	Записывают домашнее задание
Подведение итогов. Рефлексия	Выставляет оценки за работу Подводит итог	Самооценка работы на уроке

План-конспект
урока

1. Организационный момент

Приветствие.

Сегодня у нас состоится урок, посвященный определению
основных таксационным показателей древостоев, таких как: средний диаметр и
средняя высота. Знания, полученные сегодня на занятии, помогут вам и при
изучении таких дисциплин, как “Заготовка древесины и других лесных ресурсов”, “Лесоустройство”,
и конечно же, практическая деятельность любого работника лесного хозяйства
немыслима без навыков определения среднего диаметра и высоты.  Поэтому наша
задача на сегодня – разобрать, способы определения среднего диаметра и средней
высоты и научиться их рассчитывать, а для этого мы выполним несколько
практических заданий».

Тема урока: Перечислительные и измерительные методы
определения таксационных показателей древостоя (среднего диаметра, средней
высоты) (слайд 1)

Цель: систематизировать знания о таксационных
показателях, используемых в лесной таксации и ознакомится со способами
определения таксационных показателей насаждений (среднего диаметра, средней
высоты). (слайд 2)

2.
Актуализация опорных  знаний

Определение данных таксационных показателей является
основой для дальнейшей таксации древостоев, определения их запаса, вырубаемого
объема древесины на лесосеках, пробных площадях. Поэтому прежде чем перейти к
изучению новой теме, давайте вспомним, основные таксационные показатели
деревьев и как они определяются.

1) Что такое диаметр дерева, как он определяется,
единицы и точность измерения? (слайд 3)

 (Диаметр это толщина дерева на высоте 1,3 метра от
уровня земли. Определяется средним значением двух взаимно перпендикулярно
проведённых замеров. Измеряется мерной вилкой. Единица измерения – сантиметр.
Для отдельного дерева точность 0,1 см, для совокупности деревьев – ступень
толщины 2 и 4 сантиметра.) (слайд 4)

2) Что такое высота дерева, как она определяется,
единицы и точность измерения? (слайд 5)

 (Высота дерева это расстояние от шейки корня до конца
вершины. Измеряется мерной вилкой, высотомером. Единица измерения – метр. Для
отдельного дерева точность 0,1 м, для совокупности деревьев – 1 метр) (слайд
6)

3. Изучение нового материала

Теперь приступим к изучению нового материала. Рассмотрим
способы определения среднего диаметра и средней высоты при наличии данных
перечета и при их отсутствии. Начнём со среднего диаметра.

Определение среднего диаметра
древостоя.

Средний диаметр древостоя можно определить несколькими
способами.

Рассмотрим 1 способ. (слайд 7) Точное установление среднего диаметра
(с точностью до 0,1 см) применяется при таксации насаждений на пробных площадях
и при  массовой инвентаризации лесов, выполняемой при лесоустройстве и научных
исследованиях.
Ошибка в определении среднего диаметра составляет 1-5%,  Средний диаметр определяют по данным
перечета деревьев по ступеням толщины.

Произведя пе­речет, рассчитывают
суммы площадей сечений деревьев сначала в отдельных ступенях толщины, а затем
общую сумму сечений во всем таксируемом простом чистом насаждении или в
отдельном элементе сложного смешанного древостоя.

В данном случае средний диаметр определится как
диаметр круга, площадь которого равна расчетной средней площади сечения одного
дерева g_cp. Математически такое установление предполагает использова­ние
двух следующих формул:

g_cp=(g₁n₁+ g₂n₂+ g₃n₃+ …·+ g_nn_n)/(n₁+n₂+n₃+ … +n_п);

D_ср=2корень(g_ср/)π, (слайд 8)

Рассмотрим 2 способ: Средний диаметр определяют
также по данным перечета деревьев по ступеням толщины, применяется при таксации насаждений
на пробных площадях и лесосеках. Он менее точен, ошибка в определении среднего диаметра
составляет 5-10%, но это соответствует принятой точности при определении запаса
древесины при отводе лесосек – относительной точности ± 10%. 

При этом способе средний диаметр определяется как
средневзвешенная величина, не обращаясь к площадям сечений, а взвешивая числом
деревьев n сами диаметры стволов d в
ступенях толщины. (слайд 9)

В этом случае средний диаметр древостоя определяется
по следующей формуле:

Dср=(d1nl+d2n2+d3n3+ … +d nn)/(n1+
n2+ n3+ … +nn). (слайд 10)

Установленный таким расчетом средний диаметр окажется
приуменьшенным по сравнению с найденным по предыдущей формуле и не будет
полностью соответствовать другим средним величинам (Нср, gcp, Vср).
Приуменьшение среднего диаметра составит при этом 4-6 % по сравнению с
найденным через среднюю площадь сечения.

Рассмотрим 3 способ: Когда данных перечета нет. Согласно
положениям математической статистики (±25 %) для нахождения среднего диаметра с
10%-ной точностью достаточно по методу случайной выборки измерить толщину у 15
стволов и рассчитать по этим измерениям их среднеарифметическую величину.

Dср.=(d1+d2+d3+ … +dn)/(n1+ n2+ n3+
… +nn). (слайд
11)

Соответствие среднего диаметра
ступени толщины определяют с градацией 2 см, если он не превышает 20 см, и с
градацией 4 см, если он более 20 см. Это соответствует относительной точности ±
10%.

Итак, мы рассмотрели три способа
вычисления среднего диаметра.

Ответьте на вопросы:

– какой способ наиболее точный, его
точность? (Расчет через определение суммы площадей поперечного сечения, ошибка
составляет 1-5%)

– какой способ наиболее удобен и
прост в применении, его точность? (Метод случайной выборки, ошибка 10%.

Молодцы.

А теперь рассмотрим способы определения средней высоты
древостоя.

Определение средней высоты древостоя.

Высота древостоев при их инвентаризации
устанавливается с округлением до целых метров: в спелых, перестойных и
приспевающих насаждениях – раздельно по ярусам и составляющим породам, а в
молодняках и средневозрастных – только для преобладающей (главной) породы.

Рассмотрим 1 способ. Когда есть данные сплошного
перечёта.

Относительная изменчивость высот деревьев в отдельно
взятом ярусе значительно меньше относительной изменчивости толщины деревьев. Коэффициент
вариации высот обычно не превышает ± 10%. При такой изменчивости среднюю высоту
с погрешностью, ее превышающей ±0,5 м (при округлении до целых метров), можно
найти, если измерить высоты у 9 выбранных деревьев, близких к средним ступеням
толщины (центральная и две крайние), и из этих измерений рассчитать их среднюю
величину. (слайд 12)

Hср.=(h1+h2+h3+ … +hn)/(n1+ n2+ n3+ … +nn).

Рассмотрим 2 способ. Также имеются данные
сплошного перечёта. Способ называется графический. Он применяется при исследовательских
работах и на пробных тренировочных площадях, где Нср. определяют с предельно
большей точностью, которая может быть получена при значительном числе измерений
высот у отдельных деревьев. Обычно измеряют высоты у 12-15 деревьев пропорционально
отобранных каждого элемента леса с одновременным измерением их толщины на
высоте 1,3 м. (слайд 13)

При графическом определении средней
высоты строят кривую высот, представляющую собой график зависимости вы­соты
деревьев от их диаметра на уровне 1,3 м. Для построения этой кривой сначала на
графике находят местоположение точек, соответствующее парным сочетаниям высот и
диаметров у обмеренных 12 – 15 деревьев на отдельно взятой пробе. Такие точки
на графике располагаются не на одной линии, а в виде некоторой полосы
рассеянных точек. По оси рассеивания точек проводят плавную кривую линию,
которая отражает корреляционную зависимость высот стволов от их диаметров. Если
на графике восстановить ординату, соответствующую величине ранее найденного
среднего диаметра, то величина ординаты и будет средней высотой таксируемого
элемента леса. (слайд 14)

Рассмотрим 3 способ: Когда данных перечета нет.
Согласно положениям математической статистики (±25 %) для нахождения средней
высоты с 10%-ной точностью достаточно по методу случайной выборки измерить
высоту у 15 стволов средних «на глаз» и рассчитать по этим измерениям их
среднеарифметическую величину. (слайд 15)

Итак, мы рассмотрели три способа
вычисления средней высоты древостоя.

Ответьте на вопросы:

– какой способ наиболее точный? (Графический
способ определения средней высоты)

– какой способ наиболее удобен и
прост в применении, его точность? (Метод случайной выборки, ошибка 10%.)

Молодцы.

Для того, чтобы нам лучше усвоить материал, выполним
не большое самостоятельное задание. Для этого нам надо провести разбивку
на варианты.

Проведение расчетов по вариантам. В первом задании
определим средний диаметр по второму способ: Средний диаметр
определяют по данным перечета деревьев по ступеням толщины. (слайд 16)

В втором задании определим среднюю высоту графику
высот (слайд 17)

Молодцы справились с заданиями.

4. Закрепление изученного
материала

Итак, мы с вами разобрали перечислительные
и измерительные методы определения таксационных показателей древостоя (среднего
диаметра, высоты). Давайте обобщим о чем говорили сегодня на уроке. Выберете и
обоснуйте правильный ответ. (слайд 18)

1. При перечёте
деревьев их диаметры измеряют по 4-сантиметровым ступеням толщины, если средний
диаметр древостоя

а) больше 20 см

б) меньше 20 см

в) любой

2. Диаметр ствола
дерева измеряется на высоте, м

а) 1,0

б) 1,3

в) 1,5

3. Наиболее точный
метод таксации насаждений

а) измерительный

б)
перечислительный

в) глазомерный

4. Высоту дерева
можно измерить

а) полнотомером

б) буссолью

в) мерной вилкой

5. Принцип
измерения высоты дерева –

а) арифметический

б) математический

в) оптический

5.
Выдача домашнего задания

А домашним заданием  будет следующее: составить
конспект на тему «Закономерности в строении лесных насаждений и их практическое
использование».

Итак, наш урок заканчивается
и я хочу отметить, что вы все сегодня замечательно поработали. Я говорю вам
всем спасибо. (слайд 19)

6. Подведение итогов. Рефлексия

Итак, сегодня мы с вами познакомились со способами
определения таксационных показателей насаждений (среднего диаметра, средней
высоты). Работая в группе, вы общались. Как это повлияло на результат? Я
попрошу каждого оценить свою работу и общее впечатление от занятия и заполнить
анкету.

            Урок
закончен. Спасибо за работу.

Анкета

Самоанализ урока

I. Характеристика.

Урок проводился в 36 группе специальность «Лесное и
лесопарковое хозяйство». В классе присутствовало 12 человек. Данная группа
обучающихся занимается по основной программе. Непроизвольное внимание
обучающихся этого возраста становится особенно концентрированным и устойчивым
тогда, когда учебный материал отличается наглядностью, яркостью. Формируется
интерес к содержанию учебной деятельности, потребность приобретать знания.

При подготовке к этому уроку я старался учитывать
особенности психического развития обучающихся этого возраста, готовность к
сотрудничеству с преподавателем, работоспособность группы.

II. Мною был дан урок по ПМ.04 “Проведение работ
по лесоустройству и таксации

МДК. 04.01 “Лесная таксация”

 по теме: «Перечислительные и измерительные методы
определения таксационных показателей древостоя».

Тип урока: Усвоение новых знаний.

Форма проведения урока: урок – беседа.

III. Исходя из типа урока, я поставил триединые
дидактические цели:

Обучающие:

– систематизировать знания обучающихся о таксационных
показателях, используемых в лесной таксации;

– ознакомить обучающихся со способами определения
таксационных показателей насаждений и правилами пользования таксационными
приборами.

Развивающие:

– развивать у обучающихся интерес к спецдисциплине;

– развивать логическое мышление обучающихся;

– развивать зрительную память и наблюдательность.

Воспитательные:

– воспитание у обучающихся любви и чувства значимости
выбранной профессии.

IV. Главной на уроке была обучающая цель.

Следовательно, содержание учебного материала отобрано
в связи с этой целью. На уроке материал был усвоен на высоком уровне, но,
учитывая специфику обучения в области лесного хозяйства, он будет еще не раз
применен в учебном процессе.

V. Можно сказать, что все компоненты триединой
дидактической цели на каждом этапе работали в равной степени.

Наиболее оптимальной формой организации урока я считаю
фронтальную работу с учащимися.

VI. Исходя из форм организации учебного материала я
применил следующие методы обучения: познавательный, практический метод (в
Рабочей тетради записывались формулы и принципы определения средних
таксационных показателей, словесный метод (беседа), наглядный метод (работа
обучающихся с перечетными ведомостями).

Динамическая
пауза, в виде выполнения самостоятельного задания, внесла заметное оживление и
настрой обучающихся на активную работу. В течение урока обучающиеся отвечали на
поставленные вопросы, дополняли друг друга. Я думаю, что урок прошел интересно.
Соответствовал специфике, уровню подготовки обучающихся. Домашнее задание
непосредственно связано с содержанием урока, дано вовремя. Весь урок
обучающиеся заинтересованно работали, царила атмосфера доброжелательности. На
мой взгляд, урок достиг триединой дидактической цели, обучающиеся чувствовали
себя комфортно, им было интересно, и каждый мог проявить себя.

Средняя высота древостоя

Н_ср— важный таксационный показатель. В сочетании с другими показателями (возрастом, диаметром, полнотой) она служит для численной характеристики состояния и производительности как древостоя, так и качества условий местопроизрастания.

Она является основой построения многих важнейших нормативно-справочных материалов для таксации леса (бонитетных шкал, таблиц стандартных значений сумм площадей сечений и запасов и др.). В зависимости от цели и требуемой точности средняя высота может быть определена разными способами. В лесоустройстве при массовых лесоинвентаризационных работах она определяется чаще всего глазомерно (на основе навыка, приобретенного на тренировочных пробных площадях) с градацией 1 м.

В качестве придержки при определении Нср можно использовать закономерность, согласно которой средняя высота древостоя элемента леса меньше высоты самого высокого дерева примерно на 15%, и больше самого низкого на 20. 30%. В молодых древостоях эти пределы несколько расширяются.

Для контроля точности глазомерной таксации используются данные трех, пяти модельных деревьев, подобранных на глаз, близких по размерам к средним по диаметру и высоте.

На пробных площадях и при исследовательских работах Н_ср определяют более точными методами (до 0,1 м). Для этого измеряют высоты и диаметры 15..25 модельных (учетных) деревьев с последующим построением графика высот. Деревья подбирают методом пропорционально-ступенчатого представительства.

Рис. Определение средней высоты насаждения по кривой высот

Кривая высотпоказывает изменение средней высоты отдельных ступеней толщины при переходе от тонких деревьев к толстым.

Чтобы определить среднюю высоту по графику, на оси абсцисс находят место среднего диаметра. Из этой точки восстанавливают перпендикуляр до пересечения его с кривой высот. Значение ординаты точки пересечения и будет средней высотой древостоя. Из рисунка видно, что она равна 26 м.

Для определения среднеарифметической высоты каждой породы методом случайной выборки измеряют высоту 12. 15деревьев, отобранных механическим способом. Данные измерений суммируют и делят на число моделей. Исходя из коэффициента варьирования высоты, характеризуемой в среднем для всех пород 8%, ошибка в определении высоты в этом случае не будет превышать + 3 %. С целью уменьшения числа изме- ряемых деревьев до 5. 9 рекомендуется подбирать модели только из центральных ступеней толщины, следя за тем, чтобы их высота резко не отличалась от средней высоты для этих ступеней.

Определение средневзвешенной высоты требует наличия перечетной ведомости и данных измерений высот модельных деревьев по ступеням толщины. Расчет Н_ср производится по формуле:

h₁, h₂, . h_n— среднеарифметические высоты модельных деревьев отдельных ступеней толщины, м;

g1, g2, . gn — суммы площадей сечений деревьев этих ступеней, м 2 .

В смешанных и сложных насаждениях среднюю высоту яруса определяют как средневзвешенную через коэффициенты состава или запасы составляющих пород.

Пусть в древостое, имеющем состав 6С4Б, средняя высота сосны 25, а березы 22 м.Тогда средневзвешенная высота яруса равна

В последнее время для решения ряда практических задач определяют верхнюю высоту.Она вычисляется как среднеарифметическая высота 100-150 самых крупных (по высоте и диаметру, превышающим средние размеры) деревьев элемента леса.

|	следующая лекция ==>
Средний диаметр древостоя	|	БОНИТЕТ НАСАЖДЕНИЙ

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление

Генерация страницы за: 0.008 сек. —>

Источник

Характеристика рельефа по топографической карте

Орография занимается описанием внешнего облика форм зем­ной поверхности без анализа их происхождения.

ЦЕЛЬ РАБОТЫ — научиться «читать» рельеф по топо­графическим картам разного масштаба для территорий с разнооб­разным рельефом.

Студенты должны усвоить особенности отображения на топо­графических картах разных масштабов основных категорий релье­фа (горного, равнинного) и разных генетических типов рельефа (эрозионного, ледникового, эолового, карстового). После этого они изучают одну из карт для подробного анализа рельефа и его описания. В процессе выполнения задания необходимо быстро на­учиться находить на карте положительные и отрицательные формы рельефа, определять превышения их относительно друг друга, устанавливать направление и величину уклона земной поверх­ности и водных потоков, размеры отдельных форм и их ориенти­ровку на местности, а также составлять поперечные и продоль­ные профили через малые эрозионные формы (овраги, балки).

ИСХОДНЫЕ МАТЕРИАЛЫ: Рельеф изучают по учебным топографи­ческим картам масштаба I : 10000; 1: 25000. При выполнении дан­ного задания основное внимание следует сосредоточить на гори­зонталях топографической основы, отображающих рельеф местности.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. Получив карту для изучения рельефа следует:

1. Ознакомиться с масштабом карты, сечением горизонталей, шкалой заложения и географическим положением изучаемой террито­рии.

2.Установить самые общие особенности рельефа (горный или равнинный, эрозионный или ледниковый) и гидрографической сети (представлена постоянными или временными водотоками, к бассейну какой реки относится), произвести районирование территории, вы­делив участки, отличные друг от друга по внешним особенностям форм рельефа и их размерам.

Подробно изучить отдельные формы рельефа и водоемы в пределах каждого района и по возможности дать объяснения их происхождения.

4. Построить в верхнем, среднем и нижнем течении попереч­ные профили наиболее типичных эрозионных форм рельефа (речных долин, оврагов и т.п.), а также их продольные профили (рис. 1).

5. Снять необходимые количественные характеристики и про­извести необходимые измерения и морфометрические расчеты отно­сительных и абсолютных высот, средней высоты территории, шири­ны, длины и уклонов рек, рассчитать густоту и глубину расчлене­ния рельефа и т.д.

Эти измерения надо производить не в случайных пунктах, а в наиболее характерных, стараясь найти средние и крайние значе­ния измеряемой величины для данной территории.

Определение средней абсолютной высоты территории произво­дится по равенству

Источник

1.2. Определение по карте высот и

взаимного превышения точек местности

Высоты точек местности над уровнем моря (абсолютные высоты) определяют по карте с помощью отметок высот горизонталей и принятой на карте высоты сечения рельефа.

Если точка расположена на горизонтали, то ее абсолютная высота равна значению отметки этой горизонтали. Например, на рис. 6 горизонталь с отметкой 200 проходит через сарай. Это значит, что сарай расположен на высоте 200 м над уровнем моря.

В случае, когда горизонталь не имеет подписанной отметки, ее значение определяют по отметкам других горизонталей или высот точек местности. Допустим, требуется определить высоту точки местности, на которой находиться отдельный камень (рис. 6). Условный знак отдельного камня (1,3) расположен на горизонтали без отметки. Штрихи (указатели скатов) на горизонталях показывают, что скат понижается в сторону озера (Глубокое). Слева от горизонтали с отдельным камнем находится утолщенная горизонталь с отметкой 200. Высота сечения равна 10 м. Значит горизонталь проходящая через условный знак отдельного камня, имеет отметку 190, которая является высотой точки.

Если точка находится между горизонталями, то ее абсолютная высота определяется по значению отметки высоты одной из этих горизонталей. Для этого значению отметки высоты горизонтали добавляют или из нее вычитают (в зависимости от положения точки относительно горизонтали) ту часть высоты сечения, на которую точка удалена от горизонтали.

Например, нужно определить высоту развилки полевых дорог (рис. 6, точка В). Точка расположена примерно на 3/4 выше значения заложения от нижней горизонтали, имеющей отметку 220, и на 1/4 ниже – от верхней горизонтали с отметкой 230. Высота сечения рельефа 10 м. Следовательно, поправка к нижней горизонтали (220 м) составит 7,5 м, а к верхней горизонтали (230 м) – 2,5 м.

Прибавляя поправку к значению отметки нижней горизонтали или вычитая ее из значения отметки верхней горизонтали, получим высоту точки на развилке дорог:

220 м + 7,5 м = 227,5 около 227 м.

230 м – 2,5 м = 227,5 около 227 м.

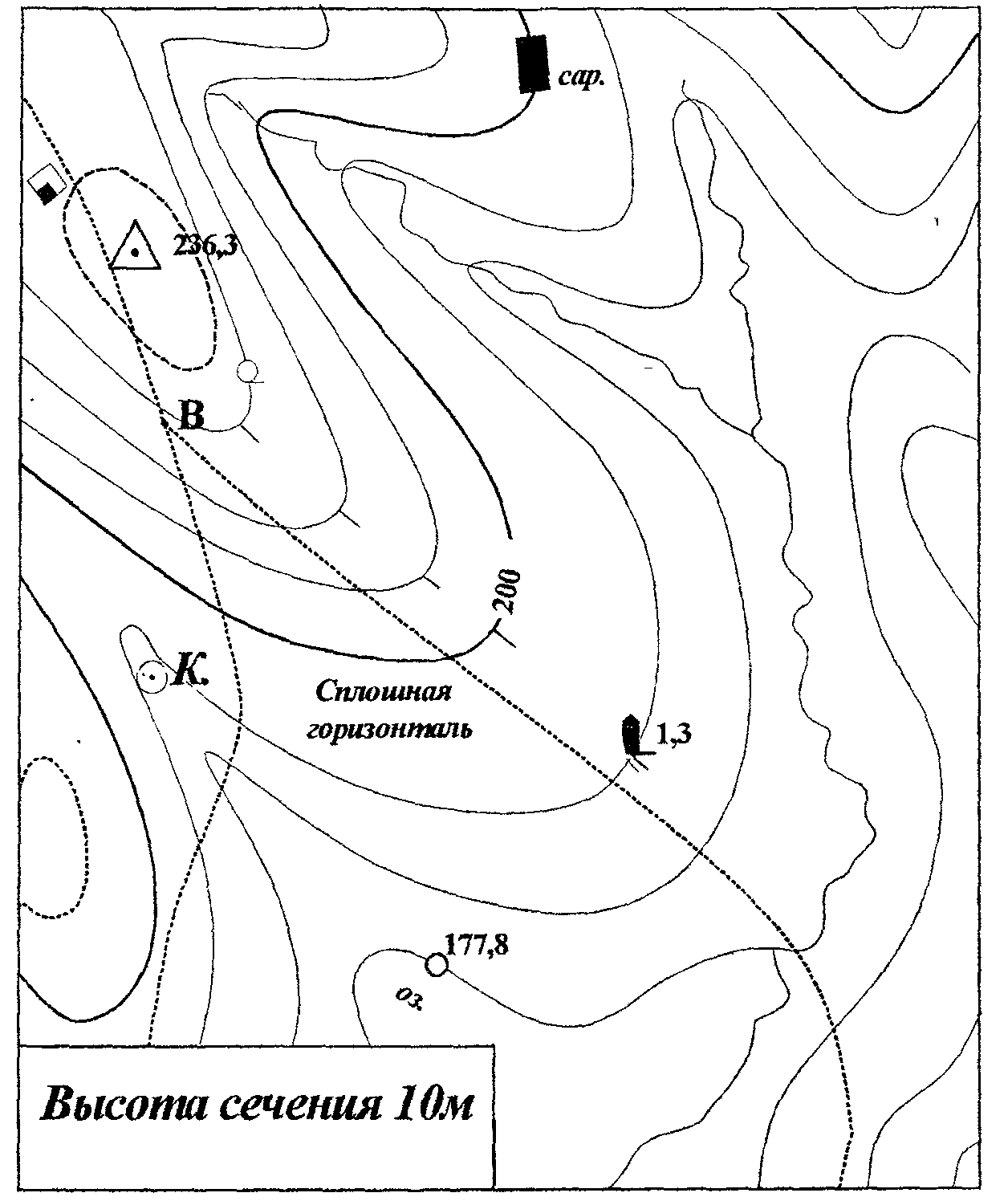
Рис. 6. Определение высоты и

взаимного превышения точек

Взаимное превышение точек местности определяется как разность его абсолютных высот. Например, превышение высоты с отметкой 236,3 (рис. 6) над оз. Глубокое (с отметкой 177,8) составляет:

Относительные высоты скатов вершин и глубины лощин удобно определять по числу промежутков между горизонталями на них. Подсчитав число промежутков между горизонталями на скате и умножив его на высоту сечения, получим относительную высоту ската. Например, на юго-западном скате высоты с отметкой 236,3 (рис. 16) имеются три промежутка между основными горизонталями и один между основной и дополнительной горизонталями. Высота сечения 10 м, поэтому относительная высота ската будет 3,5 х 10 м=35 м.

Относительные высоты (глубины) обрывов, оврагов, насыпей, выемок определяются с помощью подписей, стоящих рядом с условными знаками.

Определение по карте направления понижения и крутизны скатов. Направление понижения скатов определяется на карте по указателям скатов на горизонталях, а также путём сравнения отметок высот точек и горизонталей: понижение ската будет всегда в сторону меньшей отметки; цифры отметок горизонталей своими основаниями направлены в сторону понижения ската.

Крутизна ската определяется по значению заложения: чем меньше значение заложения, тем скат круче. На топографических картах масштаба 1:25 000, 1:50 000 и 1:100 000 основная высота сечения рельефа подобрана таким образом, что заложения между основными горизонталями в 1 см соответствует крутизна ската 1,2º (округленно до 1º).

Из этой зависимости между заложением, высотой сечения и крутизной ската можно вывести следующее правило: во сколько раз заложение меньше (больше) 1 см, во столько раз крутизна ската больше (меньше) 1º. Отсюда следует, что заложению в 1 мм соответствует крутизна ската 12º (округленно 10º), заложению в 2 мм – 6º (округлено до 5º), заложению в 5 мм – 2,4º (округлено до 2º) и т.д.

Более точно крутизна ската может быть определена при помощи специального графика, называемого шкалой заложений (рис. 7), которая располагается под южной стороной рамки карты. Вдоль горизонтального основания шкалы подписаны цифры, обозначающие крутизну скатов в градусах. На перпендикулярах к основанию отложены соответствующие им заложения.

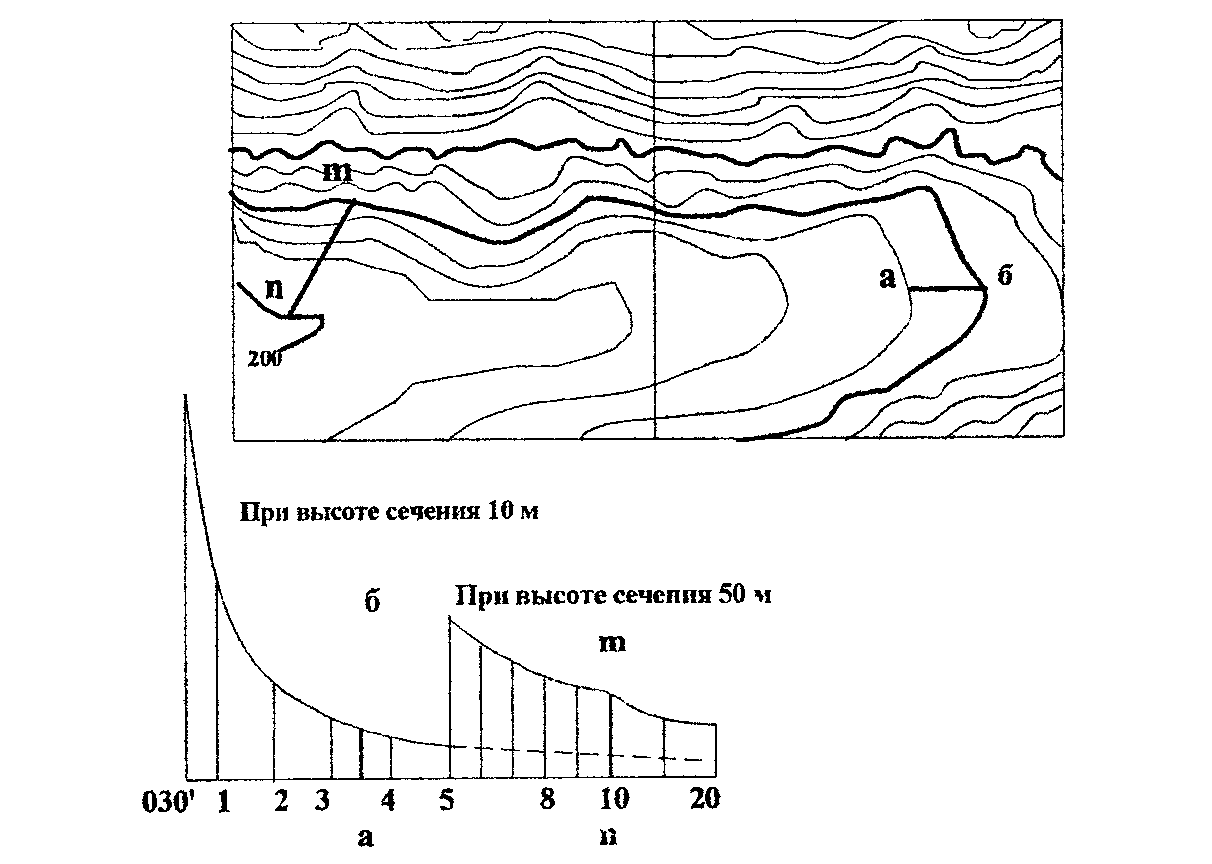
Рис. 7. Определение крутизны скатов

по шкале заложений

Шкала заложений дается для двух высот сечений: одна – для заложений между основными горизонталями, другая – для заложений между утолщенными горизонталями.

Для определения крутизны скатов по шкале заложений следует измерить расстояние между двумя смежными сплошными горизонталями в нужном направлении и отложить его на шкале заложений так, как показано на рис. 7. Отсчет внизу на шкале против отложенного отрезка укажет крутизну ската в градусах.

В нашем примере крутизна ската между точками а и б равна 3,5º. На крутых скатах, где горизонтали проходят близко одна от другой, крутизну удобнее определять по утолщенным горизонталям. Для этого измеряют отрезок между соседними утолщенными горизонталями, отложив его на правой части шкалы, как показано на рис. 7, и определяют крутизну ската. В нашем примере крутизна ската между точками n и m равна 10º.

Источник

Равнина: Восточно европейская равнина
1.Называем равнину. Находим её на карте и определяем, на каком материке, в какой части и в какой стране она находится.
2. Определяем примерную протяженность равнины с севера на юг и с запада на восток в градусах и километрах.(Вспомните, как рассчитывать расстояние на карте).
3. Определяем, как расположена равнина относительно других объектов (гор,рек,морей).
4. Определяем среднюю и максимальную абсолютные высоты равнины.
5. Определяем характер рельефа: плоский, холмистый и т.д.
6. По направлению течения рек определяем, в каком направлении происходит понижение рельефа.
7. Определяем, какие крупные реки, озёра, города находятся на равнине.
П.с. НАДО СРОЧНО.

Знаешь ответ? Добавь его сюда!

Ответить на вопрос

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Пожалуйста! С какими из перечисленных веществ: кислород, водород, гидроксид калия, натрий, бромная вода, бромоводород могут взаимодействовать а) этиловый спирт, б)фенол? Составьте уравнения возможных реакций.

Составьте структурные формулы следующих углеводородов:

• 

Мы используем файлы cookie для анализа нашего трафика. Мы также передаем информацию об использовании вами этого сайта нашим рекламным партнерам.

Закрывая этот баннер, нажимая на ссылку или продолжая просмотр другим способом, вы соглашаетесь на использование файлов cookie.

Источник