Под средней высотой поверхности над уровнем океана понимают среднее
из высот всех элементарно-малых площадок, взятых на этой
поверхности.
Представляя высоту Н поверхности функцией прямоугольных координат
карты
H=F(x, у) (1),
Запишем формулу среднего интегрального значения для двумерной
области d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”005213BB”><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
:
Где – площадь области d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”00B928B4″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
.
Формулу (2)можно представить в таком виде:
Где t wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
– профильные доли области d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”00843A45″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
, заполняющие ее без разрывов и перекрытий.
Формулу (3) можно использовать для определения в том случае, если
область d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”00E55AC0″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
можно так разделить на доли, чтобы определение средней высоты в ней
осуществлялось сравнительно просто.
Например, если за принять участки поверхности, ограниченные
соседними горизонталями, то средние высоты этих высотных поясов
будут равны полусумме отметок окаймляющих участок горизонталей.
Тогда интеграл по области (в скобках формулы 3) можно записать
так:
Где – площадь высотного пояса
И тогда с учетом формулы (4) формула (3) представляется в следующем
виде:
По формуле (5) мы получаем, что измерив площади высотных ступеней и
найдя их средние высоты (полусуммы отметок ограничивающих
горизонталей , получим данные для вычисления средней высоты
заданной области d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”006E429D”><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
.Этот способ называется планиметрическим.
Рассмотрим другой способ, точечный.
Этот способ состоит в том, что на карту наносится произвольная
сетка точек. И тогда за среднюю высоту области d
wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”00A70234″><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
принимается среднее арифметическое из высот Нк всех точек, которые
будут находиться в данной области:
Полагая, что высоты сняты в n точках, расположенных в пределах
области d wsp:val=”00FC5C93″/><wsp:rsid
wsp:val=”00FE21E7″/></wsp:rsids></w:docPr><w:body><w:p
wsp:rsidR=”00000000″
wsp:rsidRDefault=”00987C1E”><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts
w:ascii=”Cambria Math” w:h-ansi=”Cambria Math”/><wx:font
wx:val=”Cambria Math”/><w:i/><w:sz
w:val=”26″/><w:sz-cs
w:val=”26″/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr
wsp:rsidR=”00000000″><w:pgSz w:w=”12240″
w:h=”15840″/><w:pgMar w:top=”1134″ w:right=”850″
w:bottom=”1134″ w:left=”1701″ w:header=”720″ w:footer=”720″
w:gutter=”0″/><w:cols
w:space=”720″/></w:sectPr></w:body></w:wordDocument>”>
, можно рассчитать ср. кв. ошибку как ошибку репрезентативности
выборки точек по формуле:
Где – ср.кв. отклонение высоты.
Если известна ср. кв. ошибка определения высоты в точках (с учетом
ошибок карты), то соответствующая ошибка ср. высоты:
И тогда общая ср. кв. ошибка средней высоты складываются из :
Или с учетом формул (7) и (9):
Здесь δН можно найти с помощью выборки значений определяется по
нормативным документам для топокарт.
Формула (11) позволяет рассчитать число точек n, необходимых для
определения ср. высоты с заданной , если известны δ Н и mH:
Найдя необходимое число точек n, найдем расстояния между точками,
которое необходимо, чтобы соблюдалась заданная точность:
Где – площадь области .
Понравилась работу? Лайкни ее и оставь свой комментарий!
Для автора это очень важно, это стимулирует его на новое творчество!
Лекция
6
Таксационные
показатели насаждений по элементам
леса. Возраст, средний диаметр и высота.
Бонитет насаждений, бонитетные шкалы.
Полнота и сомкнутость насаждений, их
определение и взаимосвязь. Классы
товарности. Типы леса и типы условий
местопроизрастания. Таксация подроста,
подлеска, оценка напочвенного покрова
и почв.
ПЛАН
1.ВОЗРАСТ
ДРЕВОСТОЯ
2.
СРЕДНИЙ ДИАМЕТР И СРЕДНЯЯ ВЫСОТА
ДРЕВОСТОЯ
3.
БОНИТЕТ НАСАЖДЕНИЙ
4.
ТИП ЛЕСА
5.
ПОЛНОТА НАСАЖДЕНИЙ
6.
КЛАСС ТОВАРНОСТИ
Возраст
древостоя является одним из важнейших
таксационных показателей. Все основные
лесохозяйственные мероприятия (рубки
ухода, рубки главного пользования и
др.) назначаются и проводятся с обязательным
учетом возрастных этапов древостоя.
Отдельные
деревья, составляющие любой древостой
(за исключением чистых культур), обычно
различаются по возрасту. Древостой,
следует различать его преобладающему
и среднему возрасту.
Преобладающим
называют возраст, который имеют
большинство деревьев древостоя. Средний
возраст определяется как средневзвешенная
величина отдельных возрастных групп
деревьев (элементов леса) по формуле:
Aср=
(А1М1+А2М2+А3М3+…..+АnМn)/(M1+M2+M3+Mn)
где
A1,
А2,…,
Аn
— возрасты отдельных групп или поколений
деревьев, слагающих древостой (ярус),
лет;
M1,
М2,…,
Мn—
их запасы, м3.
Например,
в еловом древостое, состоящем из двух
возрастных поколений, 70 % запаса приходится
на 120-летние деревья, а 30 % — на 80-летние.
Средний возраст этого древостоя равен
Aср=(120*70+80*30)/100=108
лет
тогда
как преобладающим возрастом является
120 лет. Чем однороднее древостой, тем
меньше разница между средним и
преобладающим возрастами.
Определение
запаса элемента леса дело сложное и
трудоемкое. Учитывая то, что запасы
составляющих древостой элементов леса
прямо пропорциональны их суммам площадей
сечений (ΣG), приведенную выше формулу
можно записать
Аср=(А1*G1+A2G2+……+An*Gn)/(G1+G2+…….Gn)
где:
G1,
G2,…
Gn
–
суммы
площадей сечений отдельных элементов
леса на круговых пробных площадках.
В
чистых простых древостоях его средний
возраст часто определяют как
среднеарифметический возраст отдельных
деревьев, взятых в качестве моделей.
При этом для определения возраста
моделей пользуются возрастным буравом
(растущие деревья), или подсчитывают
число годичных слоев на пнях (срубленные
деревья).
У
молодых деревьев сосны (до 50… 60 лет)
возраст можно определить подсчетом
числа мутовок на стволе. В смешанных и
сложных насаждениях возраст определяется
отдельно для каждого элемента леса.
При
лесоинвентаризации за единицу измерения
возраста принимается не 1 год, а некоторый
период называемый классом
возраста.
Величина
класса возраста для разных пород
установлена в зависимости от
продолжительности их жизни и возраста
рубки. Для хвойных и твердолиственных
древостоев семенного происхождения с
большей долговечностью продолжительность
класса возраста принята равной 20 годам.
Для мягколиственных и твердолиственных
древостоев порослевого происхождения
– 10 годам.
При
массовой таксации в первом случае
возраст древостоя определяется с
градацией 10 лет, во втором – 5 лет. Для
древостоев, состоящих из быстрорастущих
пород (тополя, ивы, акации) с очень низким
возрастом их рубки (до 30…40 лет), класс
возраста принят равным 5 годам. Иногда
для долговечных пород с очень высокими
возрастами рубки (кедр) допускаются
40-летние классы возраста. Классы возраста
обозначаются римскими цифрами.
Древостой
считается одновозрастным, если деревья
имеют разницу в возрасте не превышающую
продолжительность одного класса
возраста. Если разница больше, то такой
древостой относится к разновозрастному.
Древостои
из светолюбивых пород (сосны, лиственницы)
чаще всего одновозрастные, а из
теневыносливых (ели, пихты) – разновозрастные.
Между
морфологическими признаками деревьев
и их возрастом существуют корреляционные
зависимости. Поэтому в практике
лесоинвентаризационных работ средний
возраст древостоев чаще всего определяют
по внешним признакам деревьев:
-
Высоте
и диаметру с учетом их зависимости от
условий местопроизрастания, -
Форме
кроны, -
Углу
ветвления сучьев, -
Цвету
и строению коры (ее трещиноватости) и
т. д.
В
таксационных описаниях каждый древостой
характеризуется классом возраста и
преобладающим возрастом.
В
смешанных и сложных древостоях возраст
определяется по элементам леса. Древостой
в целом относится к тому классу
возраста,
который имеет преобладающий
элемент леса,
например 4С
(160)
ЗС (100) ЗБ (70).
В
разновозрастных
древостоях, где поколения выделить
трудно, указываются нижний
и верхний пределы возраста. Средний
возраст определяется по возрасту
преобладающего числа деревьев, например
10E (110,
80 – 120) .
Для
решения ряда практических задач классы
возраста объединяют в группы
возраста: молодняки,
средневозрастные, приспевающие, спелые
и перестойные. Исходным основанием для
деления насаждений по группам возраста
является принятый возраст рубки.
Распределение насаждений по группам
возраста при возрасте рубки 101… 120 лет
(VI класс) показано в табл.
Распределение
насаждений по группам возраста
|
Группа возраста |
Молодняки |
Средневозрастные |
Приспе- вающие |
Спелые |
Перес- тойные |
|||
|
Классы возраста |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
|
Возраст, лет |
1-20 |
21-40 |
41-60 |
61-80 |
81-100 |
101-120 |
121-140 |
141- 160 |
Как
правило, к
молоднякам относятся древостои первых
двух классов возраста; спелыми считаются
древостои, относящиеся к классу возраста
рубки и следующего за ним класса; к
приспевающим
– один класс возраста, предшествующий
спелым; все остальные классы возраста,
которые находятся между молодняками и
приспевающими древостоями, считаются
средне- возрастными.
Для
численной характеристики древостоя
определяют средний диаметр Dcp
и среднюю высоту Нср
деревьев. Эти два таксационных показателя
находятся в тесной зависимости. С
увеличением диаметров деревьев
увеличивается и их высота. Эта связь
характеризуется выпуклой кривой.
Способы
определения этих показателей базируются
на закономерностях строения древостоев
по диаметру и высоте и в зависимости от
требуемой точности могут быть различными.
При проведении лесоустройства средний
диаметр и среднюю высоту часто определяют
визуально.
При
отводе и таксации лесосек или работе
на пробных площадях, требующих большей
точности, необходимы специальные
измерения. Например, чтобы определить
средний диаметр нужно иметь перечетную
ведомость, характеризующую распределение
числа стволов в древостое по ступеням
толщины, а для определения средней
высоты – еще и данные измерения высоты
модельных или учетных деревьев.
Средний
диаметр древостоя
Dср
это средняя толщина древесных стволов
на высоте 1,3 м (высота груди человека
среднего роста) от шейки корня дерева.
Различают
среднеарифметический и среднеквадратический
диаметры. Среднеарифметический диаметр
определяется как частное от деления
суммы диаметров всех деревьев элемента
леса на число деревьев. Среднеквадратический
(таксационный) диаметр
определяется через среднюю площадь
сечения путем деления суммы площадей
сечений деревьев всех ступеней толщины
на общее число деревьев.
gср
=
ΣG/N
= πD2cр/4
Dср=2*корень(gср/π)
Из
всех способов определения среднего
диаметра этот способ является наиболее
точным, так как дерево, имеющее
среднеквадратический диаметр, будет
близким к среднему и по другим таксационным
показателям — высоте и объему.
Между
среднеарифметическим и среднеквадратическим
диаметрами существует зависимость,
согласно которой последний всегда
больше первого.
Dср.
кв=
корень(D2ср.
ариф.+σ2)
|
При n=Vd2/P2 где: |
В
лесоустройстве при массовой таксации
лесов средний диаметр определяется с
градацией 2 см (при среднем диаметре
древостоя до 32 см) и 4 см (при большем
среднем диаметре).
В
приспевающих, спелых и перестойных
древостоях средний диаметр устанавливается
раздельно по элементам леса, а в молодняках
и средневозрастных – только для
преобладающей породы.
Для
приближенных расчетов среднего диаметра
рекомендуют способы, основанные на
закономерностях строения насаждений,
согласно которым среднее дерево в
древостое в общем ряду распределения
деревьев по ступеням толщины занимает
строго определенное место. Так в
древостое, состоящем из одного элемента
леса, средний диаметр составляет около
60 % диаметра самого толстого дерева и
примерно в 2…2,3 раза больше диаметра
самого тонкого; около
60
% общего числа деревьев древостоя имеют
диаметр меньше среднего, а 40% больше
его.
Средняя
высота древостоя
Нср–
важный
таксационный показатель. В сочетании
с другими показателями (возрастом,
диаметром, полнотой) она служит для
численной характеристики состояния и
производительности как древостоя, так
и качества условий местопроизрастания.
|
Она
В |
В
качестве придержки при определении Нср
можно использовать закономерность,
согласно которой средняя высота древостоя
элемента леса меньше высоты самого
высокого дерева примерно на 15%, и больше
самого низкого на 20…30%. В молодых
древостоях эти пределы несколько
расширяются.
Для
контроля
точности
глазомерной
таксации
используются данные трех, пяти модельных
деревьев, подобранных на глаз, близких
по размерам к средним по диаметру и
высоте.
На
пробных площадях и при исследовательских
работах Нср
определяют более точными методами (до
0,1 м). Для этого измеряют высоты и диаметры
15..25 модельных (учетных) деревьев с
последующим построением графика высот.
Деревья подбирают методом
пропорционально-ступенчатого
представительства.

Рис.
Определение средней высоты насаждения
по кривой высот
Кривая
высот
показывает
изменение средней высоты отдельных
ступеней толщины при переходе от тонких
деревьев к толстым.
Чтобы
определить среднюю высоту по графику,
на оси абсцисс находят место среднего
диаметра. Из этой точки восстанавливают
перпендикуляр до пересечения его с
кривой высот. Значение ординаты точки
пересечения и будет средней высотой
древостоя. Из рисунка видно, что она
равна 26 м.
|
Для |
Определение
средневзвешенной высоты требует наличия
перечетной ведомости и данных измерений
высот модельных деревьев по ступеням
толщины. Расчет Нср
производится по формуле:
Нср
=(h1*g1+h2*g2+h3*g3+…….+hn*gn)/(g1+g2+g3+…..gn)
где:
h1,
h2,
… hn—
среднеарифметические высоты модельных
деревьев отдельных ступеней толщины,
м;
g1,
g2, … gn – суммы площадей сечений деревьев
этих ступеней, м2.
В
смешанных и сложных насаждениях среднюю
высоту яруса определяют как средневзвешенную
через коэффициенты состава или запасы
составляющих пород.
Пусть
в древостое, имеющем состав 6С4Б, средняя
высота сосны 25, а березы 22 м.
Тогда
средневзвешенная высота яруса равна
Нср
=(25*6+22*4)/10=23,8
м
В
последнее время для решения ряда
практических задач определяют верхнюю
высоту. Она
вычисляется как среднеарифметическая
высота 100-150 самых крупных (по высоте и
диаметру, превышающим средние размеры)
деревьев элемента леса.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
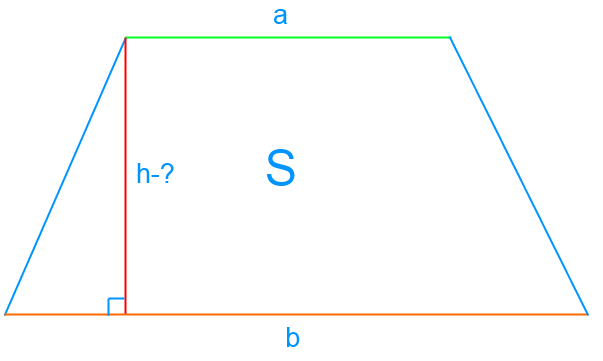
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
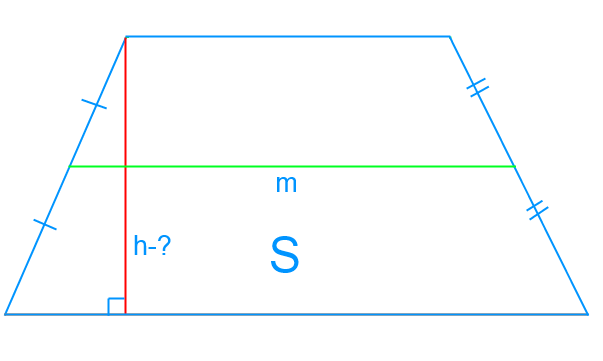
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
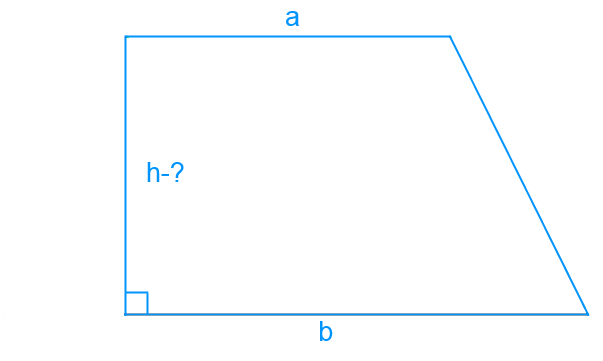
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
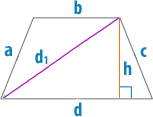
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.
Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.

После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.

Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.

Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.

В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.

Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.

Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.
Может еще поучимся? Загляни сюда!
Формулы трапеции
❓Инструкция
 Калькулятор для нахождения площади, средней линии и высоты трапеции.
Калькулятор для нахождения площади, средней линии и высоты трапеции.
 Как пользоваться:
Как пользоваться:
 Необходимо выбрать неизвестную величину трапеции
Необходимо выбрать неизвестную величину трапеции Указать известные величины
Указать известные величины Получить ответ
Получить ответ
 Ответ возможно получить с этапами решения, если выставить галочку «Подробнее».
Ответ возможно получить с этапами решения, если выставить галочку «Подробнее». Также, есть возможность указать точность ответа. То есть количество знаков после запятой.
Также, есть возможность указать точность ответа. То есть количество знаков после запятой.
 Ограничения:
Ограничения:
Числа на входе должны быть: Вещественными
Вещественными Больше 0, но не больше 100 000.
Больше 0, но не больше 100 000. С точностью не более 10 знаков после запятой.
С точностью не более 10 знаков после запятой.
📖 Теория
трапеция
 Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, у которой пара противоположных сторон параллельна (отмечены стрелками ниже):
Трапеция представляет собой 4-стороннюю плоскую форму с прямыми сторонами, у которой пара противоположных сторон параллельна (отмечены стрелками ниже):

 Трапеция:
Трапеция:
 имеет пару параллельных сторон
имеет пару параллельных сторон является равнобедренной, если боковые стороны равны и углы при основаниях попарно равны.
является равнобедренной, если боковые стороны равны и углы при основаниях попарно равны.

 Площадь трапеции
Площадь трапеции
Площадь трапеции равняется полусумме оснований, умноженную на высоту.
$$S = frac{a + b}{2} * h$$, где $$S$$ — площадь, $$a,b$$ — основания трапеции, $$h$$ — высота.
 Периметр трапеции
Периметр трапеции
Периметр является суммой длин всех сторон :
$$P = a + b + c + d$$, где $$P$$ — периметр, $$a,b,c,d$$ — стороны трапеции.
 Медиана трапеции
Медиана трапеции
Медиана (называемая также средней линией) представляет собой отрезок линии на полпути между двумя основаниями.
Средняя линия трапеции равняется полусумме оснований.
$$m = frac{a + b}{2}$$, где $$m$$ — средняя линия трапеции, $$a,b$$ — основания трапеции.
Посмотрев на формулу площади трапеции, а затем на формулу средней линии, мы легко можем заметить, что площадь трапеции также можно найти как среднюю линию, умноженную на высоту.
$$S = m * h$$
 Высота трапеции
Высота трапеции
Высоту трапеции можно найти при известных площади и средней линии трапеции как:
$$h = frac{S}{m}$$, где $$h$$ — высота, $$S$$ — площадь, $$m$$ — средняя линия трапеции.
А также при известных площади и двух оснований трапеции следующим образом:
$$h = frac{2S}{a + b}$$, где $$h$$ — высота, $$S$$ — площадь, $$a,b$$ — основания трапеции.
Последняя формула опять же вытекает из формулы средней линии трапеции.
➕ Примеры
 Пример 1: Две стороны трапеции имеют длину 6 м и 4 м и высоту 3 м. Какова его площадь?
Пример 1: Две стороны трапеции имеют длину 6 м и 4 м и высоту 3 м. Какова его площадь?
$$S = frac{6 м + 4 м}{2} * 3 м = 5 м * 3 м = 15 м^2$$.
 Пример 2: Трапеция имеет длины сторон 5 см, 12 см, 4 см и 15 см, каков ее периметр?
Пример 2: Трапеция имеет длины сторон 5 см, 12 см, 4 см и 15 см, каков ее периметр?
$$P = a + b + c + d = 5 см + 12 см + 4 см + 15 см = 36 см$$.
 Пример 3: Найдите высоту трапеции, если площадь трапеции равна $$28 см^2$$, а сумма длин оснований равна 14 см.
Пример 3: Найдите высоту трапеции, если площадь трапеции равна $$28 см^2$$, а сумма длин оснований равна 14 см.
Способ 1: Воспользуемся формулой $$h = frac{S}{m}$$, нам известна площадь $$S = 28 см^2$$, а также сказано, что сумма длин оснований равна 14 см. То есть $$a + b = 14см$$.
Найдем среднюю линию $$m$$ по формуле $$m = frac{a + b}{2} = frac{14}{2} = 7см$$
А значит, $$h = frac{S}{m} = frac{28см^2}{7см} = 4см$$
Способ 2: Воспользуемся второй формулой (см. раздел теория)
$$h = frac{2S}{a + b}$$, нам дано $$S = 28 см^2$$ и $$a + b = 14см$$
подставляем в формулу.
$$h = frac{2 * 28 см^2}{14 см} = frac{56 см^2}{14 см} = 4 см$$.

