Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
1) длину ребра А1А2;
из координат А2 вычти координаты А1
получишь вектор А1А2 с 3 координатами
их возведи в квадрат
сложи
извлеки из суммы квадратов корень
2) угол между ребрами А1А2 и А1А3;
найди координаты А1А2 и А1А3; (как в первом пункте)
найди длины обоих ((как в первом пункте))
найди скалярное произведение их:
первую координату первого умножь на первую координату второго+
+вторую координату первого умножь на вторую координату второго+
+третью координату первого умножь на третью координату второго
скалярное произведение подели на обе длины- получишь косинус угла между ними
3) площадь грани А1А2А3 ;
векторы А1А2 и А1А3 ты уже нашел в пункте 2
их длины тоже
есть два пути найти площадь:
ПЕРВЫЙ
найти векторное произведение этих векторов
потом его длину
потом его длину поделить на 2
это будет площадь треугольника
ВТОРОЙ
длины сторон (векторов) ты знаешь
косинус угла щнаешь
найди синус и считай площадь треугольника
4) объем пирамиды А1А2А3A4
векторы А1А2 и А1А3 ты уже нашел в пункте 2
найди еще А1А3 так же
запиши координаты всех трех в определитель по строкам (или по столбцам)
модуль определителя деленный на 3 и будет объем пирамиды
5) длину высоты пирамиды, проведенной из вершины A4.
объем= площадь грани А1А2А3 умножить на высоту и делить на 3
Пример 1:
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
1) координаты и модули векторов А1 А2и А1 А4;
2) угол между ребрами А1 А2и А1 А4;
3) площадь грани А1 А2 А3;
4) объем пирамиды;
5) уравнение прямой А1 А2;
6) уравнение плоскости А1 А2 А3;
7) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
Сделать чертеж.
А1 (0; 4; -4), А2 (5; 1; -1), А3 (-1; -1; 3), А4 (0; -3; 7).
Решение от преподавателя:



Пример 2:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
1. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
Решение от преподавателя:






Пример 3:

Решение от преподавателя:
Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-3)(1*2-0*3) – (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y – 3z-38 = 0
Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
Уравнение прямой A1A4: ![]()
γ = arcsin(0.267) = 15.486o
Уравнение высоты пирамиды через вершину A4(0,2,2)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0 ![]()
![]()
Уравнение плоскости через вершину A4(0,2,2)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
2(x-0)+13(y-2)-3(z-2) = 0
или
2x+13y-3z-20 = 0
Пример 4:

Решение от преподавателя:
Даны координаты пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
- Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-0)(3*2-8*3) – (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x – 15y + 33z-18 = 0
Упростим выражение: -6x – 5y + 11z-6 = 0
2) Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
Уравнение прямой A1A4: 


γ = arcsin(0.193) = 11.128o
3) Уравнение высоты пирамиды через вершину A4(0,5,4)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0


4) Уравнение плоскости через вершину A4(0,5,4)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости
Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
-6(x-0)-5(y-5)+11(z-4) = 0
или
-6x-5y+11z-19 = 0
5) Координаты вектора A1A4(0;4;3)
Уравнение прямой, проходящей через точку А1(0,1,1) параллельно вектору А1А2(0,4,3) имеет вид:

Пример 5:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:




Пример 6:

Решение от преподавателя:
1) Даны координаты вершин пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
Координаты векторов.
Координаты векторов: A1A2(3;3;3) A1A4(0;4;3)
Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 


Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:  , где a1a2 = X1X2 + Y1Y2 + Z1Z2
, где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(3;3;3) и A1A3(0;4;3):

А1 = arccos(0,808)
Найдем площадь грани с учётом геометрического смысла векторного произведения:
S =![]()
Найдем векторное произведение
=i(3*2-8*3) – j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i – 15j + 33k

3) Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
Координатывекторов:A1A2(3;3;3) A1A3(-3;8;2) A1A4(0;4;3) :
|
|
|
где определитель матрицы равен:
∆ = 3*(8*3-4*2)-(-3)*(3*3-4*3)+0*(3*2-8*3) = 39
Пример 7:

Решение от преподавателя:
- Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):
γ = arccos(0) = 90.0030 - Площадь грани
Площадь грани можно найти по формуле:
где
Найдем площадь грани A1A2A3
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):

Площадь грани A1A2A3 - Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
|
|
|
где определитель матрицы равен:
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18
Пример 8:
Даны координаты вершин пирамиды А1А2А3А4 . Найти:
1) длину ребра А1А2;
2) угол между рёбрами А1А2 и А1А4 ;
3) угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объём пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
Сделать чертёж.
А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8).
Решение от преподавателя:
1) Длина ребра A1A2;

2) угол между ребрами А1А2 и А1А4;

3) угол между ребрами А1А4 и гранью А1А2А3;

Найдем уравнение стороны А1А4:

Вектор нормали: ![]() к плоскости А1А2А3.
к плоскости А1А2А3. ![]()

4) площадь грани А1А2А3;
![]()
5) объем пирамиды;

6) уравнение прямой А1А2;

7) уравнение плоскости А1А2А3;

Итак: z=4 – уравнение плоскости А1А2А3.
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
A4O – высота:
Уравнение A4O:
![]()
Т.к. ![]() , то
, то
![]()
В результате получаем уравнение высоты:
![]()


Пример 9:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:


Векторная алгебра и элементы аналитической геометрии
ЗАДАЧА 1
В декартовой прямоугольной системе координат даны вершины пирамиды А1 В1 С1 D1. Найдите:
А) длину ребра А1 В1;
Б) косинус угла между векторами ![]() ;
;
В) уравнение ребра А1 В1;
Г) уравнение грани А1 В1 С1;
Д) уравнение высоты, опущенной из вершины D1 на грань А1 В1 С1;
Е) координаты векторов ![]() ,
, ![]() ,
, ![]() , и докажите, что они образуют линейно независимую систему;
, и докажите, что они образуют линейно независимую систему;
Ж) координаты вектора ![]() , где
, где ![]() – середины ребер А1 D1 и В1 С1 соответственно;
– середины ребер А1 D1 и В1 С1 соответственно;
З) разложение вектора ![]() по базису
по базису ![]() если А1(–2,2,2), В1(1,–3,0), С1(6,2,4), D1(5,7,–1).
если А1(–2,2,2), В1(1,–3,0), С1(6,2,4), D1(5,7,–1).
Решение
А) Найдем координаты вектора ![]() по формуле
по формуле
![]() =
= ![]() XВ
XВ ![]() – XА
– XА ![]() ; YВ
; YВ ![]() – YА
– YА ![]() ; ZВ
; ZВ ![]() – ZА
– ZА ![]()
![]() , где (ХА
, где (ХА ![]() , YА
, YА ![]() , ZА
, ZА ![]() ) – координаты точки А1, (ХВ
) – координаты точки А1, (ХВ ![]() , YВ
, YВ ![]() , ZВ
, ZВ ![]() ) – координаты точки В1.
) – координаты точки В1.
Итак, ![]() =
= ![]() Тогда
Тогда ![]() =
= ![]() .
.
Итак, длина отрезка ![]() (или длина вектора
(или длина вектора ![]() ) равна
) равна ![]() . Это и есть искомая длина ребра.
. Это и есть искомая длина ребра.
Б) Координаты вектора ![]() =
= ![]() уже известны, осталось определить координаты вектора
уже известны, осталось определить координаты вектора ![]() :
: ![]() =
= ![]() .
.
Угол между векторами ![]() и
и ![]() вычислим по формуле Cos
вычислим по формуле Cos ![]() =
= 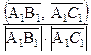 ,
,
Где скалярое произведение векторов ![]() и
и ![]() равно (
равно ( ![]() ,
, ![]() )= 3 ´ 8 + (–5) ´ 0 + (–2) ´2 = 24 + 0 – 4=20,
)= 3 ´ 8 + (–5) ´ 0 + (–2) ´2 = 24 + 0 – 4=20, ![]() =
= ![]() ,
, ![]() =
= ![]()
Итак, Cos ![]() =
= ![]() =
= ![]() .
.
В) Координаты точки А1(–2,2,2) обозначим соответственно Х0 = –2, У0 = 2, Z0=2, а координаты точки В1 (1,–3,0) через Х1=1, У1 = –3, Z1=0 и воспользуемся уравнением прямой в пространстве, проходящей через две точки: ![]() .
.
Следовательно, уравнение ребра А1В1 имеет вид ![]() или
или ![]()
Г) Обозначим координаты векторов ![]() и
и ![]() через Х1=3, У1= –5,
через Х1=3, У1= –5, ![]() 1= –2 и Х2=8, У2= 0,
1= –2 и Х2=8, У2= 0, ![]() 2=2 соответственно. Векторное произведение данных векторов определяется формулой
2=2 соответственно. Векторное произведение данных векторов определяется формулой
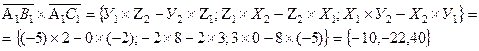
Так как данный вектор перпендикулярен грани А1 В1 С1 то можно воспользоваться уравнением плоскости, проходящей через точку (Х0, У0, ![]() 0) перпендикулярно вектору
0) перпендикулярно вектору ![]() , которое имеет вид
, которое имеет вид
А ![]() .
.
Подставим координаты точки А1 (Х0=–2, У0=2, ![]() 0=2) и координаты перпендикулярного вектора А=–10, В=–22, С=40 в это уравнение:
0=2) и координаты перпендикулярного вектора А=–10, В=–22, С=40 в это уравнение:
– 10 ( Х + 2 ) – 22 (У – 2) + 40 ( ![]() – 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (– 20 + 44–80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: –10х – 22у + 40 z–56=0 или
– 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (– 20 + 44–80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: –10х – 22у + 40 z–56=0 или
–5х – 11у + 20 z – 28=0.
Д) Вектор ![]() является направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку
является направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку ![]() с заданным направляющим вектором:
с заданным направляющим вектором: ![]() , где
, где ![]() – координаты точки D1. Отсюда искомое уравнение:
– координаты точки D1. Отсюда искомое уравнение: ![]() или
или ![]()
Е) Координаты вектора ![]() =
= ![]() =
= ![]() .
.
Обозначим ![]()
![]() =
= ![]() ,
, ![]()
![]() =
= ![]() ,
, ![]() .
.
Чтобы доказать, что векторы ![]() образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
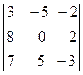 отличен от 0. Определитель третьего порядка равен
отличен от 0. Определитель третьего порядка равен
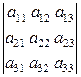 =
= 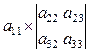 –
– 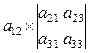 +
+ 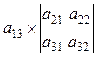 =
=
= ![]()
Вычислим определитель
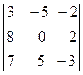 =3
=3 ![]() – (–5)
– (–5) ![]() +(–2)
+(–2) ![]() = 3
= 3 ![]() (0
(0 ![]() (–3) – 5
(–3) – 5 ![]() 2)+5
2)+5 ![]() (8
(8 ![]() (–3) – 7
(–3) – 7 ![]() 2) –
2) –
– 2 ![]() (8
(8 ![]() 5 – 7
5 – 7 ![]() 0) =3
0) =3 ![]() (–10)+5
(–10)+5 ![]() (–24 – 14) – 2
(–24 – 14) – 2 ![]() 40=–30 – 190 – 80 = –300.
40=–30 – 190 – 80 = –300.
Так как данный определитель отличен от 0, то вектора ![]() образуют линейно независимую систему.
образуют линейно независимую систему.
Ж) Сначала найдем координаты точек М и N соответственно. Координаты точки
М = 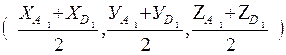 =
= ![]() =
= 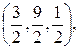
N = 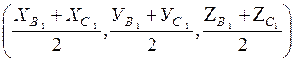 =
= 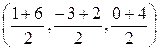 =
= 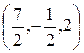 .
.
Получаем вектор ![]() =
= ![]() .
.
З) Обозначим через ![]() координаты вектора
координаты вектора ![]() в базе
в базе ![]() .
.
Тогда ![]() =
= ![]() =
= ![]() .
.
Так как
![]() =
= ![]() +
+ ![]() +
+ ![]() ;
; ![]()
= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
То приравнивая соответствующие координаты, получим систему трех линейных уравнений с тремя неизвестными.
(1) 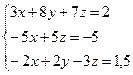
Решим данную систему уравнений с помощью формул Крамера (см. ![]() глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
(2) 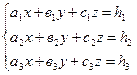
Тогда ![]() =
= ![]() z
z ![]() , где
, где
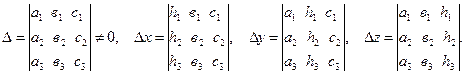
Для системы (1) определитель
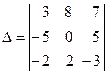 =3
=3 ![]() –8
–8 ![]() +7
+7 ![]() =
=
= 3 ( –10) – 8 ![]() ( 15 + 10 ) + 7 ( –10) = –30 – 200 – 70 = –300;
( 15 + 10 ) + 7 ( –10) = –30 – 200 – 70 = –300;
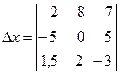 = 2
= 2 ![]() –8
–8 ![]() +7
+7 ![]() =
=
![]()
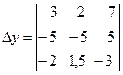 =3
=3 ![]() –2
–2 ![]() +7
+7 ![]() =
=
=3 ![]()
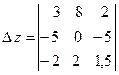 =3
=3 ![]() –8
–8 ![]() +2
+2 ![]() =
=
= ![]()
По формулам Крамера ![]()
![]()
Итак, разложение вектора ![]() по базису (
по базису ( ![]() ) имеет вид
) имеет вид
![]() =
= ![]()
ЗАДАЧА 2
Решите систему линейных уравнений
А) методом Крамера;
Б) методом Гаусса;
В) с помощью обратной матрицы.
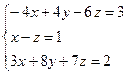
Решение
А) Метод Крамера состоит в решении системы линейных уравнений по формулам Крамера ![]() ,
,
Где ![]() (Подробности смотрите в пункте З) задачи 1.
(Подробности смотрите в пункте З) задачи 1.
Так как ![]()
![]()
![]()
![]() ; то
; то ![]()
Б) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.
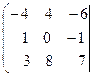
![]()
Поменяем местами первую и вторую строки матрицы чтобы в ее левом верхнем углу была единица. Получим матрицу,
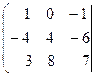
![]()
Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид,
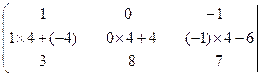
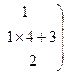 =
= 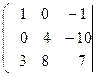
![]()
Умножим каждый элемент первой строки матрицы на –3, и прибавим полученные числа к соответствующим элементам третьей строки. Получим:
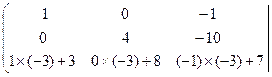
 =
= 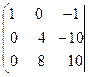
![]() .
.
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.
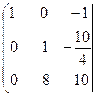
![]() .
.
Умножим каждый элемент второй строки матрицы на –8 и прибавим полученные числа к соответствующим элементам третьей строки:
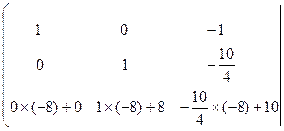
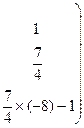

![]() .
.
Данная матрица соответствует системе уравнений 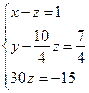 , решение которой совпадает с решением исходной системы. Начиная с последнего уравнения, несложно найти все неизвестные.
, решение которой совпадает с решением исходной системы. Начиная с последнего уравнения, несложно найти все неизвестные.
Действительно, так как ![]() и
и ![]() , то
, то ![]()
Отсюда, ![]() Из
Из ![]() имеем
имеем ![]()
Ответ: ![]() .
.
В) Решение системы в этом случае равно ![]() =
= ![]()
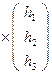 , где
, где ![]() =
= 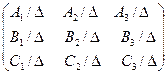 – обратная матрица для матрицы
– обратная матрица для матрицы ![]() =
= 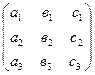 ,
, ![]() – столбец свободных членов,
– столбец свободных членов, ![]() – определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
– определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
Составим матрицу состоящую из коэффициентов при неизвестных данной системы:
А = 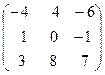 .
.
Вычислим ее определитель 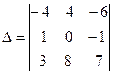 = –4
= –4 ![]() –4
–4 ![]() –6
–6 ![]() =
=
= ![]() .
.
Вычислим алгебраические дополнения для всех элементов матрицы А:
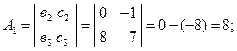
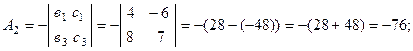
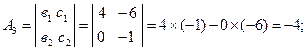
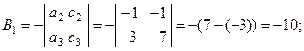
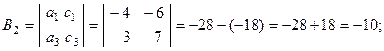
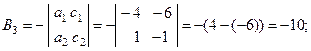
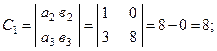
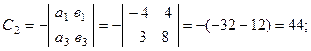
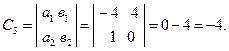
Тогда ![]()
![]() =
= 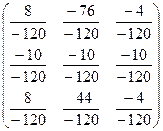 =
= 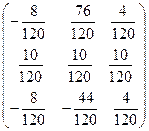 и
и
![]() =
= 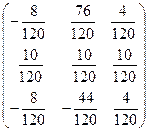
![]()
![]() =
=
= 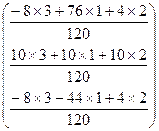 =
= 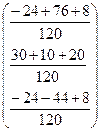 =
= 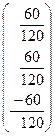 =
= ![]() .
.
Отметим, что ответы, полученные при решениями разными методами совпадают между собой.
Ответ: ![]()
| < Предыдущая | Следующая > |
|---|



