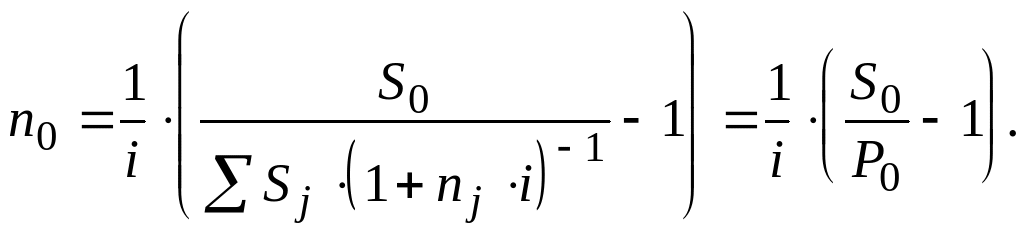Как найти срок консолидированного платежа

Если при объединении платежей задана
величина консолиди-рованного платежа
S₀ , то
возникает проблема определения срока
его платежа n₀
. В этом случае уравнение эквивалентности
удобно представить в виде равенства
современных стоимостей соответствующих
платежей.

При применении простой ставки это
равенство имеет вид:

(6)

отсюда

(7)

Здесь

– современная величина консолидированных
платежей.

№ 37. Суммы в размере 10, 20 и 15 тыс.
руб. должны быть выплачены через 50, 80 и
150 дней соответственно. Стороны
договорились заменить их одним платежом
в сумме 50 тыс. руб. Определить срок этого
платежа при условии начисления 10%
годовых.

Решение. Найдем современную
стоимость заменяемых платежей:

руб.

Тогда

года, или

дней.

При применении простых учетных ставок
расчет n₀
производится по формуле

(8)

где

– современная стоимость консолидированных
платежей.

№ 38. Суммы в размере 1,2, 1,5 и 2,3 млн.
руб. должны быть выплачены через 35, 55 и
75 дней соответственно. Достигнуто
соглашение об объединении всех платежей
в один, равный 5,5 млн. руб., с исполь-зованием
для этого простой учетной ставки в 7%.
Определить срок уплаты консолидированного
платежа.

Решение. Найдем современную
стоимость консолидированного платежа:

млн. руб.

Тогда

года, или 1 год 165 дней.

Таким образом, срок платежа переносится
на 1 год и 165 дней с момента получения
кредита.

При использовании сложных процентных
ставок срок уплаты консолидированного
платежа определяется по формуле:

(9)

где

.

№ 39. Два платежа по 1,4 и 1,9 млн. руб.
со сроками погашения через 2 и 3 года
соответственно, объединяются в один
платеж, равный 4 млн. руб., с использованием
сложной процентной ставки в 6%. Определить
срок консолидированного платежа.

Решение. Найдем современную
стоимость платежей:

млн. руб.

Тогда

года.

§ 3. Общий случай изменения условий коммерческих сделок

Обсудим теперь более общие случаи
изменения условий выплат, предусматриваемых
в контрактах, для которых решение не
всегда можно получить простым суммированием
платежей, приведенных на некоторую
дату. Разумеется, что и в таких случаях
решение основывается на принципе
эквивалентности платежей до и после
изменения условий контракта. И
решение заключается в разработке уже
упоминавшегося выше уравнения
эквивалентности.

Если приведение платежей осуществляется
на некоторую начальную дату, то уравнение
эквивалентности в общем виде имеет вид:

а) при использовании простых процентов:

;
(10)

б) при использовании сложных процентов:

.
(10)

Здесь

и

параметры заменяемых платежей, а

и

параметры заменяющих платежей.

Конкретный же вид уравнений эквивалентности
зависит от условий контракта, поэтому
методику составления таких уравнений
удобнее рассмотреть на примерах.

№ 40. Две суммы – 100 и 50 тыс. руб. –
должны быть выплачены 1 ноября и 1
января (следующего года). Стороны
согласились пересмотреть порядок
выплат: должник должен выплатить 1
декабря 60 тыс. руб., а остаток долга гасит
1 марта. Найти эту сумму при условии, что
пересчет осуществляется по ставке
простых процентов, равной 20%.

Решение. Возьмем за базовую
дату, например, 1 января следующего года.
Тогда, учитывая, что

01.11 – 305-ый день,

01.12 – 335-ый день,

01.03 – 60-ый день,

можно составить уравнение эквивалентности

или

то есть,

руб.

Следует
отметить, что при применении простых
процентных ставок изменение базовых
дат приводит к некоторым, впрочем
незначительным изменениям результатов.
Например, если привести платежи к 1
марта, то получим уравнение эквивалентности:

откуда следует, что

руб.

Отмеченная зависимость результатов
от выбора базовой даты объясняется тем,
что если

,
то

№ 41. Пусть в условиях № 40 по новому
обязательству выплаты необходимо
произвести равными суммами 1 декабря и
1 марта. Найти эту сумму.

Решение. Примем в качестве
базовой даты 1 января. Тогда

или

То есть

=
77.224,55 руб.

Теперь перейдем к примеру со сложной
процентной ставкой.

№ 42. Строительная фирма получила
в банке долгосрочный кредит в размере
10 млн. руб. под 10% годовых сроком на 5 лет.
Впоследствии стороны пересмотрели
условия займа и выработали новые: через
3 года выплачивается 4 млн. руб., а остальная
сумма выплачивается через 4 года после
первой выплаты. Определить сумму
окончательного платежа.

Решение. Составим уравнение
эквивалентности, приняв за базовую дату
момент получения кредита:

или

То есть,

руб.

Отметим, что изменение базовой даты
при применении сложных процентов не
влияет на результаты расчетов по замене
платежей, так как, если

,
то

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

АНО ВПО
«Региональный финансово-экономический институт»
ФИНАНСОВАЯ
МАТЕМАТИКА
(Вторая лекция)
______________________________
http://elearning.rfei.ru
Содержание
РАЗДЕЛ 1. ИНФЛЯЦИЯ ………………………………………………………….. 3
Глава 1.1. Основные понятия ………………………………………………… 3
Глава 1.2. О случаях учета инфляции ……………………………………. 7
РАЗДЕЛ 2. КОНСОЛИДАЦИЯ И ПРОЛОНГАЦИЯ
ФИНАНСОВЫХ ОБЯЗАТЕЛЬСТВ ………………………………………… 13
Глава 2.1. Эквивалентные обязательства …………………………….. 13
Глава 2.2. Постановка задач на консолидацию
и пролонгацию ……………………………………………………………………. 14
РАЗДЕЛ 3. КРЕДИТЫ ……………………………………………………………. 20
Глава 3.1. Планирование погашения долгосрочной
задолженности ……………………………………………………………………. 20
Глава 3.2. Планирование погасительного фонда ………………….. 21
Глава 3.3. Погашение долга в рассрочку ……………………………… 25
Глава 3.4. Погашение потребительского кредита…………………. 29
2
РАЗДЕЛ 1. ИНФЛЯЦИЯ
Глава 1.1. Основные понятия
Вы решили приобрести однокомнатную квартиру весной
2012 г. в г. Курске. В экологически чистом районе стоимость новой «однушки» составляла 1,2 млн. руб., но вдруг обстоятельства
изменились, и вы решаете отложить покупку на лето. Но цены
выросли до 1,45 млн. руб. С чем это связано? Вероятнее всего, с
ожиданием роста цен на жилье покупатели активизировались, и
повышенный спрос повлек за собой рост цен на жилье. Значит,
один и тот же товар стал стоить дороже. Таким образом, можем
говорить об инфляции.
Итак, инфляция – падение покупательной способности денег (обесценивание денег).
В экономике различают более 20 видов инфляции: инфляция, связанная: с эмиссией денег; с большими кредитными расходами; с превышением спроса над предложением; с ожиданием
роста цен; с изменением цен на сырье; с ростом заработной платы
и т. д.
Различают скрытую и открытую инфляции. Скрытой инфляции присущи дефицит товаров, отложенный спрос и постоянные цены. При открытой инфляции освобождаются цены и растут
доходы.
Освобождение цен при накопившихся излишках денег
ускоряет обращение денег в десятки раз в связи с боязнью населения нового витка повышения цен, что приводит к гиперинфляции. В экономике существует еще одно важное понятие – дефляция, т. е. сдерживание обесценивания денег, или мероприятия по
ограничению денежной массы в обращении.
Это осуществляется путем увеличения налогов, повышения
процентных ставок, ограничения кредитов, снижения роста заработной платы, ограничения продажи ценных государственных
бумаг на открытом рынке.
Если вернуться к рассмотренным ранее разделам курса, при
определении наращенных сумм все денежные величины принимались по номиналу. Т. е. не принималось во внимание снижение
3
реальной покупательной способности денег за период, охватываемый операцией. На самом же деле инфляция в денежных отношениях играет заметную роль, и без ее учета чаще всего конечные результаты чисто условны (взять хотя бы пример с покупкой
«однушки»).
А потому инфляцию нужно учитывать, по крайней мере в
двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой
операции.
Это означает, что с точки зрения финансовой математики
можно вводить характеристики инфляции.
Одной из характеристик инфляции является индекс цен, о
котором вы узнали из курса статистики (там его обозначали буквой I , в нашем курсе этой буквой мы обозначаем доход). Поэтому обозначим индекс цен как J p (читается «джи»).
Индекс цен показывает, во сколько раз приросли цены за
соответствующий период.
Jp
цена в отчетном периоде
.
цена в базисном периоде
(1.1)
Если вернуться к примеру с покупкой «однушки», то индекс цен будет равен J p
1,45
1,21.
1,2
С индексом цен функционально связана еще одна из характеристик инфляции – индекс покупательной способности J c .
Причем эта связь находится в обратной зависимости, т. е.
Jс
1
.
Jp
(1.2)
Индекс покупательной способности показывает, во сколько
раз уменьшилась покупательная способность за этот же период.
1
Jp
На примере «однушки» J с
0,83.
Вспомните, наращенную сумму денег (измеренную по номиналу) мы обозначали буквой S . А теперь нам потребуется ввести еще один показатель – наращенную сумму с учетом ее обесценивания, мы ее обозначим буквой C .
4
Очевидно, что
C S Jc .
(1.3)
Например, пусть сегодня получены 5 000 руб. Известно,
что за три предшествующих года цены возросли в 5 раз, т. е.
Jp
5 , тогда J с
1
и реальная стоимость С сегодняшних денег в
5
деньгах трехлетней давности будет равна С = 5 000
1
= 1 000 руб.
5
Еще одной из характеристик, обозначенных в названии темы, является темп инфляции.
Темп инфляции h – относительный прирост цен за период,
измеряется в %. Он связан с индексом цен по формуле
(1.4)
h 100 (J p 1) .
Следовательно,
Jp 1
h
.
100
(1.5)
Например, если цены увеличились в 2 раза, то их прирост
составил h 100 (2 1) 100% .
И наоборот, если темп прироста цен составил 70%, то цены
увеличились в J p 1
70
1,7 раза.
100
Инфляция является цепным процессом. А потому индекс
цен за несколько периодов равен произведению цепных индексов
цен, т. е.
Jp
(1
h1
h2
hn
) (1
) … (1
).
100
100
100
(1.6)
Если h – постоянный ожидаемый (или прогнозируемый)
темп инфляции за один период, то за n таких периодов получим
Jp
(1
h n
) .
100
(1.7)
Из этой формулы можно получить показатель среднегодового темпа инфляции, т. е.
h 100 ( n J p 1)
(1.8)
Иногда при получении обобщающего показателя темпа инфляции за некоторый период времени суммируют (а не умножа-
5
ют, как должно быть!) показатели, что приводит к занижению
темпа инфляции.
Например, постоянный темп инфляции на уровне 5% в месяц на молочные продукты приведет к росту цен за год в размере
Jp
(1
h n
)
100
(1 0,05)12 1,796 .
Таким образом, действительный темп инфляции составил
79,6%, а если бы суммировали, то всего 60% .
Почему так? Мы 12 месяцев года умножали бы на 5%.
Задача 1.1
Темп инфляции h=10% в месяц. Найти рост цен за год и годовой темп инфляции на табачные изделия.
Решение.
h 100 ( n J p
Jp
1) ; 10 100 (12 J p
1
(
1)12 1,112
10
1) ; 1 10(12 J p
1) ; 12 J p
1
1;
10
3,1384 .
Это говорит о том, что цены выросли за год в 3,1384 раза,
но это не останавливает курильщиков. Как вероятно и не остановят дальнейшие меры правительства по увеличению стоимости
табачных изделий и алкогольной продукции. Если возвратиться к
событиям, например, до 2011 г., то в России пачку сигарет можно
было купить за 12 руб., а бутылку пива приобрести на каждом
углу 24 часа в сутки дешевле, чем бутылку питьевой воды. Возможно, что запрет продажи алкогольной продукции и табачных
изделий поможет в оздоровлении нашей нации. А мы снова возвращаемся к решаемой нами задаче.
Итак, чтобы узнать годовой темп инфляции, воспользуемся
формулой 1.4 и получим: h 100 (J p 1) 100 (3,1384 1) 213,84%.
Задача 1.2
Последовательный прирост цен за 3 летних месяца на хлебобулочные изделия в отдельных регионах ЦАО составил 25%,
20% и 18%. Найти темп инфляции за эти три месяца.
6
Решение.
Воспользуемся формулой 1.6.
Jp
(1
25
20
18
) (1
) (1
) 1,77 .
100
100
100
Это означает, что цены выросли в 1,77 раза, или на
h 100 (J p 1) 100 (1,77 1) 77% .
Вероятно, это связано с тем, что среднегодовая урожайность зерновых в России (на нечерноземах) – около 17 центнеров
(на 2011 г.), а, например, в Германии, Франции, Англии (на нечерноземах) – около 70 центнеров. А потому высок процент потребности России в продовольствии за счет импортных поставок.
Глава 1.2. О случаях учета инфляции
Снова вернемся к мысли о том, что инфляцию нужно учитывать, по крайней мере в двух случаях: при расчете наращенной
суммы денег и при измерении реальной эффективности (доходности) финансовой операции.
Итак, выясним, как учитывать инфляцию при расчете
наращенной суммы.
Мы уже вводили обозначения:
S – наращенная сумма, пусть С – та же сумма с учетом инфляции. Тогда по формуле 1.3 с учетом инфляции получим:
S
.
Ip
C S Iс
(1.9)
Вспомним, что наращенная сумма простых процентов
определяется как S K (1 ni) . Подставив значение наращенной
суммы в предыдущую формулу 1.9, получим:
C
K (1 ni)
Ip
K (1 ni)
.
h n
(1
)
100
(1.10)
Для сложных процентов наращенная сумма S K(1 i) n . Тогда с учетом 1.9 получаем
n
C
K (1 i) n
Ip
K (1 i) n
h
(1
)
100
7
K
n
1 i
h
1
100
.
(1.11)
Еще раз подчеркнем, что математика является аппаратом
исследования финансовых ситуаций. А это значит, что
если i
h
, то в правой части последней формулы числи100
тель больше знаменателя, а с точки зрения финансов это означает
реальный рост суммы денег;
если i
h
– нет реального роста денег, и это явление
100
называют «эрозией» капитала (проанализируйте это с точки зрения математики);
если i
h
– наращение поглощается инфляцией.
100
Задача 1.3
Снова возвратимся к задаче 1.2, где последовательный прирост цен за 3 летних месяца на хлебобулочные изделия в отдельных регионах ЦАО составил 25%, 20% и 18%. Найти реальную
сумму 1,5 млн. руб., накопленные проценты и инфляционную
сумму, реальный доход, реальную доходность, если наращение
идет по ставке i=50%
а) сложных годовых,
б) простых процентов.
Решение.
Индекс инфляции найден нами в задаче 1.2. Цены за 3 месяца увеличились в 1,77 раз.
Рассчитаем реальную сумму 1,5 млн. руб.
а) по сложным процентам:
Наращенная
сумма
по
сложным
процентам
3
S K (1 i) n
1,5 (1 0,5) 12
1,66 млн.руб.
Тогда реальная стоимость 1,66 млн. руб. с учетом инфляции
по формуле 1.9 будет такой: C
S
Ip
1,66
1,77
0,938 млн.руб.
Накопленные проценты
I = S – K = 1,66 – 1,5 = 0,16 млн. руб.;
8
Найдем инфляционную сумму (сумму, которую «съела»
инфляция), обозначив ее символом K h .
Kh
S C ; Kh
1,66 0,938 0,722 млн. руб. ;
Тогда реальный доход, который назовем I 1 , будет равен
I1
C K ; I1
0,938 1,5
0,562 млн. руб. ;
вычислим реальную доходность i
I1
;i
Kn
i
I1
Kn
0,562
3
1,5
12
1,5
150%.
Какой вывод из результатов решения этой части задачи?
Вывод следующий: сложная годовая ставка 50% при
трехмесячной инфляции 77% дает отрицательную годовую доходность 150%.
Приступим к решению второй части задачи (б) по простым
процентам).
Наращенная сумма по простым процентам будет определяться в соответствии с уже известной вам ранее формулой
S K (1 ni) .
S 1,5(1
3
0,5) 1,6875 млн. руб.
12
Реальная стоимость 1,6875 млн. руб. с учетом инфляции по
простым процентам будет находиться по формуле 1.9 как C
Тогда C
1,6875
1,77
S
.
Ip
0,953 млн. руб.
Далее аналогично сложным процентам находим накопленные проценты I S K 1,6875 1,5 0,1875 млн. руб.;
инфляционная сумма K h будет равна
K
h
S C 1,6875 0,953 0,7345 млн. руб.;
реальный доход I1 C K ; I1 0,953 1,5
реальная доходность i
I1
;i
Kn
9
0,547
3
1,5
12
0,547 млн. руб.
1,46
146%.
И снова, как в предыдущем случае, делаем вывод о том, что
простая годовая ставка 50% при трехмесячной инфляции
77% дает годовую отрицательную доходность 146% .
Теперь приступим к рассмотрению второго случая учета
инфляции: при измерении эффективности (доходности) финансовой операции.
В этом случае применяется индексация процентной ставки,
которая сводится к увеличению ставки процентов на величину
так называемой инфляционной премии.
Назовем ставку с поправкой на инфляцию брутто-ставкой
и обозначим ее r (ставка i + маржа).
Напомним, что маржой мы называли надбавку к изменяющейся во времени базовой ставке (об этом шла речь в первой
лекции).
Для нахождения брутто-ставки составляется уравнение эквивалентности множителей наращения по брутто-ставке и по
ставке i с учетом инфляции.
Рассчитаем брутто-ставки:
1. Для простых процентов:
Уравнение эквивалентности имеет вид:
(1.12)
1 nr (1 ni) I p ,
следовательно, брутто-ставка
r
реальная ставка i
(1 ni) I p 1
n
,
1 nr
1
.
1
Ip
n
(1.13)
(1.14)
2. Для сложных процентов:
Уравнение эквивалентности имеет вид:
h n
) ,
100
h
h
следовательно, брутто-ставка r i
,
i
100
100
1 r
1.
реальная ставка i
h
1
100
(1 r ) n
(1 i) n (1
10
(1.15)
(1.16)
(1.17)
Еще раз подчеркнем, что основная идея принципа эквивалентности – получать одинаковый финансовый результат, по
какой бы ставке не начислялись проценты.
Задача 1.4
Продолжим решать задачу 1.3. В условиях этой задачи рассчитаем брутто-ставки для годовой простой и сложной ставки
50%.
В этих случаях просто необходимо воспользоваться формулами брутто-ставки для простых и сложных процентов, т. е.
формулами 1.13 и 1.16.
а) Брутто-ставка простых процентов
r
(1 ni) I p 1
(1
n
3
0,5) 1,77 1
12
3,965.
3
12
Итак, вычисленная брутто-ставка показывает, что простая
годовая ставка 396,5% годовых компенсирует инфляцию и дает
реальный доход 50% годовых.
Чтобы убедиться в правильности вычислений, найдем проверкой наращенную сумму денег с учетом инфляции по бруттоставке:
1,5 1 3,965
S
1,77
3
12
1,6875 млн. руб.
И найдем наращенную сумму по ставке i без учета инфляции:
S 1,5 1 0,5
3
12
1,6875 млн. руб.
Как видите, они совпадают, значит, расчет верен. Но обратите внимание на формулы, по которым мы определяли наращенные суммы. Мы не указывали их номер, чтобы вы еще раз
внимательно обратились к той части лекции, где шла речь о вычислении наращенной суммы с учетом и без учета инфляции. б)
Брутто-ставка сложных процентов
11
Т.к. ставка i – годовая ставка, то темп инфляции h должен
быть рассчитан за год по формуле 1.7: J p
(1
h n
) .
100
Наша задача – выразить h . А для этого возведем обе части
равенства в степень
1
(можно было сказать, что извлечем из
n
обеих частей равенства корень n-ой степени).
1
Получим:
(J p ) n
1
h
,
100
1
откуда
(J p ) n
1
h
,
100
тогда
1
h ((J p ) n 1) 100.
Если вы внимательно изучаете курс, то заметили, что в финансовой математике все расчеты несложные. Нужно просто
внимательно их выполнять.
Возвращаясь к решаемой нами задаче, говорим, что теперь
только осталось в выведенную нами формулу для темпа инфляции h подставить данные задачи. Тогда получим:
1
3
h
100 (1,77 12
1)
4
100 (1,77 – 1)
881,5%
– на столько про-
центов увеличились цены за год.
r 0,5
881,5 881,5
0,5 13,7225 1372,25%
100
100
Снова делаем вывод:
годовая сложная брутто-ставка r = 1372,25% компенсирует инфляцию и дает годовой доход 50% .
Но, как и в случае простых процентов, сделаем проверку.
1) Наращенная сумма денег с учетом инфляции по бруттоставке r:
3
12
1,5 (1 13,7225)
S
1,77
1,66 млн. руб.
2) Наращенная сумма по ставке i без учета инфляции:
S 1,5(1 0,5)
3
12
1,66 млн. руб.
Они совпали, значит, наши расчеты верны.
12
РАЗДЕЛ 2. КОНСОЛИДАЦИЯ И ПРОЛОНГАЦИЯ
ФИНАНСОВЫХ ОБЯЗАТЕЛЬСТВ
Глава 2.1. Эквивалентные обязательства
Вопрос, к рассмотрению которого мы сейчас приступаем,
все ближе вас подводит к решению финансовых задач не на бытовом, а на профессиональном уровне.
Дело в том, что когда мы вели речь о депозитах и кредитах,
то это в принципе уже должно было быть известно любому человеку, и не только получающему экономическое образование.
Практически нередко возникают случаи, когда необходимо
изменить условия финансовых сделок. Например, взяв кредит
под определенный процент, клиент банка его добросовестно гасит, но потом у него поменялись финансовые возможности, и он
решает погасить задолженность по кредиту досрочно.
Он идет в банк за консультацией: как ему это сделать?
Возможна и такая ситуация: клиент брал один кредит, затем возникла необходимость взять второй, и он решает объединить (консолидировать) несколько платежей в один. И в этой
ситуации ему нужна консультация от специалиста банка.
Иногда возникает финансовая необходимость в продлении
платежей, такую финансовую процедуру называют пролонгацией финансовых обязательств, и снова необходимо знать возможности проведения этой процедуры.
В рассмотренных двух ситуациях – консолидировании и
пролонгации – прибегают к принципу финансовой эквивалентности обязательств, который предполагает неизменность финансовых отношений сторон до и после изменения контракта
(принцип финансовой эквивалентности мы уже рассматривали с
точки зрения наращенной суммы).
Еще раз поясняем, что эквивалентными считаются такие
платежи, которые, будучи «приведены» к одному моменту времени, оказываются равными. Приведение осуществляется путем
дисконтирования к более ранней дате или, наоборот, наращения
суммы платежа, если эта дата относится к будущему.
13
Две суммы денег S1 и S 2 , выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные
(или наращенные) величины, рассчитанные по одной и той же
процентной ставке и на один момент времени, одинаковы.
Общий метод решения задач на консолидирование и пролонгацию заключается в разработке уравнения эквивалентности,
в котором сумма заменяемых платежей, приведенных к некоторому моменту времени, называемому базовым, приравнивается к
сумме платежей по новому обязательству, приведенных к той
же дате.
Глава 2.2. Постановка задач на консолидацию и пролонгацию
Итак, как мы уже сказали, наиболее распространенным
способом изменения условий контрактов является консолидация
(объединение) и пролонгация (продление) финансовых обязательств.
Какие практические задачи здесь решаются?
В этих ситуациях, как правило, рассматриваются два типа
задач:
1) при известных суммах платежей и их сроках, известном
сроке объединяемого платежа находится его сумма;
2) при известных суммах платежей и их сроках, известной
сумме консолидированного платежа находится срок его
выплаты.
(Можно сказать, что рассматриваются две взаимно обратные задачи).
Итак, пусть рассматривается задача о нахождении суммы
консолидированного (объединенного) платежа при известных
сроках выплат всех платежей
Здесь можно рассмотреть 3 случая.
Случай 1.
Консолидированный платеж S0 расположен между консолидируемыми платежами. Другими словами, есть платежи до и
после консолидированного платежа, рисунок 2.1.
Расположим платежи на временной оси в порядке возрастания их дат.
14
S1
S2
S0
Sj
Sk-1
Sk
t
n1
n2
nj
nk-1
n0
nk
Рисунок 2.1
Найдем величину консолидированного платежа S 0 , используя простую процентную ставку i.
Платежи S1 , S 2 , S j производятся раньше консолидированного платежа S 0 , поэтому они наращиваются.
Платежи S k 1 , S k производятся позднее консолидированного платежа S1 , поэтому они дисконтируются.
Формула для расчета консолидированного платежа будет
выглядеть так:
S0
S j (1 (n 0
Sk
n j ) i)
j
k
1 (n k
n0 ) i
. (2.1)
Внешне формула выглядит довольно сложно и громоздко,
но если внимательно ее проанализировать, то вот что получим.
Первое слагаемое – суммы платежей по простой ставке (к
каждому слагаемому этой суммы применяется формула 2.3
(наращение по простой ставке) из первой лекции); второе слагаемое – суммы платежей дисконтирования – формула 2.4 из второй
лекции.
На примере задачи, которую мы рассмотрим чуть ниже, вам
станет понятно, как применять эту громоздкую формулу.
Случай 2
Консолидированный платеж S0 расположен раньше всех
консолидируемых платежей, рисунок 2.2.
S0
S2
S3
Sk-1
Sk
t
n0
n2
n3
nk-1
Рисунок 2.2
15
nk
Формула для расчета консолидированного платежа будет
выглядеть так:
Sk
S0
k
1 (n k
n0 ) i
.
(2.2)
Случай 3.
Консолидированный платеж S0 расположен позднее всех
консолидируемых платежей, рисунок 2.3.
S1
S3
S2
S0
Sk
t
n1
n3
n2
nk
n0
Рисунок 2.3
Формула для расчета консолидированного платежа будет
выглядеть так:
S0
S j (1 (n 0 n j ) i).
(2.3)
j
Если подвести итог рассмотрению трех случаев, то первый
случай – объединение второго и третьего.
Ну а дальше рассмотрим практическую ситуацию, позволяющую разобраться с формулами.
Задача 2.1
Для поэтапного выполнения ремонта цехов по производству упаковочной тары компания ГРИНН взяла три кредита:
S1 1 млн. руб., S 2 2 млн. руб., S3 3 млн. руб. со сроками
уплаты соответственно через 100, 120 и 150 дней, которые по финансовым обстоятельствам заменяются одним кредитом со сроком уплаты через 180 дней при простой ставке 20%. Найти сумму
консолидированного платежа (год принять равным 360 дней).
Решение
Платежи и даты их выплат изобразим точками на временной оси (рисунок 2.4) в порядке возрастания дней выплат:
S1
S2
S3
S0
t
100 дн.
120 дн.
150 дн.
Рисунок 2.4
16
180 дн.
За базовую дату примем день выплаты консолидированного
платежа S 0 .
Т. к. срок объединяемых платежей меньше срока платежа
S 0 (случай 3), то приведение платежей к моменту выплаты консолидированного платежа S 0 будет выполняться с помощью операции наращения.
Мы будем использовать формулу 2.3 из этой лекции:
S0
S j (1 (n 0
n j ) i).
j
Но в этой формуле внимательно рассмотрим сомножители
S j . Это те три суммы, которые нам известны, они соответственно
равны одному, двум и трем миллионам рублей.
Периоды n 1 , n 2 , n 3 – это сроки платежей, которые соответственно равны отношению разности окончательного и планируемого платежа к числу дней года (по условию берем 360 дней).
Процентная ставка –20%. И т. к. идет наращение, то все суммы
суммируются. В итоге получаем:
S0
S1 (1 n 1i) S2 (1 n 2 i) S3 (1 n 3i) 1 (1
2 (1
180 100
0,2)
360
180 120
180 150
0,2) 3 (1
0,2) 6,161 млн. руб.
360
360
Теперь, как мы уже говорили, рассмотрим обратную задачу.
Итак, вторая задача – нахождение срока консолидированного платежа при известных суммах выплат всех платежей.
В этом случае все платежи приводятся на одну более раннюю дату операцией дисконтирования, рисунок 2.5.
S1
S2
S3
S0
Sk-1
n1
n2
n3
n0
nk-1
Sk
t
nk
Рисунок 2.5
Составляется уравнение эквивалентности, в левой части которого стоит дисконтированная стоимость платежа S 0 , а в правой –
сумма дисконтированных стоимостей объединяемых платежей P0.
17
Решаем задачу, используя ставку i. Запишем уравнение эквивалентности, дисконтируя все платежи, включая S 0 на начальную дату «0».
S0
1 n 0i
k
Sk
.
1 n ki
Обозначим через P0 сумму дисконтированных стоимостей
объединяемых платежей, т. е. P0
k
куда 1 n 0i
S0
Sk
, тогда
1 n 0i
1 n ki
P0 , от-
S0
, в результате получим срок консолидированного
P0
платежа
n0
S0
1
1
.
P0
i
(2.4)
Итак, мы вывели формулу для расчета срока консолидированного платежа, но давайте снова проанализируем ее с точки
зрения финансовой математики, используя чисто математический
анализ. Очевидно, что в полученной формуле консолидированная
стоимость платежей S0 должна быть больше суммы дисконтированных консолидируемых платежей P0 (числитель будет больше знаменателя, значит, дробь будет больше единицы, а разность
этой дроби и единицы будет тогда числом положительным). В
противном случае срок платежа n0 получится отрицательным.
Снова рассмотрим практическую ситуацию.
Задача 2.2
Строительная фирма в погашение задолженности банку за
предоставленный кредит под 70% годовых должна произвести 2
платежа в сроки 18.05 (138-й день), 1.09 (244-й день) суммами
S1 2,7 млн. руб. и S 2 3,5 млн. руб. Фирма договорилась объединить оба платежа в один суммой S0
7,0 млн. руб. с продле-
нием срока выплаты.
Найти срок выплаты консолидированного платежа. (В
скобках указан порядковый номер даты платежа).
18
Решение.
Срок выплаты консолидированного платежа найдем по
только что полученной формуле 2.4, где P 0 – современная величина консолидируемых платежей, которая будет найдена как
сумма двух дисконтных платежей, см. формулу 2.4. из первой
лекции, т. е.
P0
S1
S2
1 n1 i 1 n 2 i
2,7
3,5
138
244
1
0,7 1
0,7
360
360
4,5 млн. руб.
Вычислив современную величину консолидируемых платежей, теперь найдем срок выплаты консолидированного платежа, n 0
7,0
1
1
4,5
0,7
0,7937 года.
Далее найдем порядковый номер дня года, в который нужно погасить платеж. Для этого считаем, что в году 365 дней и
умножаем их на получившуюся долю года, т. е. на 0, 7937. В итоге получим 365 0,7937 290 дней. По календарю невисокосного
года отсчитываем 290 дней – это будет 17 октября.
Обращаем ваше внимание еще и на то, что при подсчете
суммы консолидированных платежей мы вычисляем обыкновенные или коммерческие проценты, а потому выполняем деление
на 360 дней.
19
РАЗДЕЛ 3. КРЕДИТЫ
Глава 3.1. Планирование погашения долгосрочной
задолженности
Всем, наверное, когда-то приходилось занимать деньги в
долг или давать кому-то в долг и, как правило, это осуществлялось не на коммерческой основе. В советские времена считалось
неприличным требовать с должника какую-то сумму сверх той,
что бралась в долг. И если взаймы бралась достаточно крупная
сумма и на длительный срок, то благодарный должник возвращал
деньги вместе со скромным подарком (коробкой конфет, бутылкой вина и т. п.). Но время изменило поведение людей, и сейчас,
как мы уже говорили в первой лекции, стало не зазорным давать
деньги в долг под проценты. Помните, в первой лекции мы говорили о существовании процентщиков. Так вот, в XXI в. они предлагают свои услуги нуждающимся в финансовой помощи на
определенных условиях. Развешивают объявления в подъездах
домов, в лифтах, предлагают свои услуги через интернет. Вероятно, что кто-то этими услугами пользуется. Ведь коль есть предложение, значит, оно отвечает какому-то спросу.
Но основная часть граждан пользуется при финансовых затруднениях возможностями банков, благо, что их сейчас более
чем достаточно. А для того чтобы выбрать наиболее выгодный
вариант займа, необходимо хорошо разбираться в условиях кредитования. И это тем более важно для тех, кто планирует свою
деятельность связать с работой в банке.
Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Например, погашение задолженности в рассрочку (кредит), периодическое поступление доходов от
инвестиций, выплата пенсий и т.д.
Такие последовательности называются потоком платежей,
а отдельный элемент последовательности – членом потока.
Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы,
называется финансовой рентой или аннуитетом.
20
Но мы в этой главе поведем речь о кредите не с точки зрения нахождения наращенной суммы, а с разработки плана погашения займа, который состоит в составлении графика периодических платежей должника. И для ведения разговора на профессиональном уровне введем ряд понятий и обозначений.
Расходы должника обычно называются срочными уплатами или расходами по займу.
Методы определения размера срочных уплат зависят от
условий погашения долга, которые предусматривают:
срок займа n;
уровень и вид процентной ставки g (простая; сложная, проценты выплачиваются 1 раз в году, m раз в году);
методы уплаты процентов (сразу на всю сумму или с дальнейшим распределением одинаковыми суммами по периодам,
или проценты начисляются на непогашенный остаток долга);
способы погашения основной суммы долга (погашение основного долга равными суммами или погашение всей задолженности срочными уплатами).
Введем обозначения:
D сумма задолжника (основная сумма без процентов);
Y срочная уплата;
I проценты по займу;
R расходы по погашению основного долга;
g ставка процентов по займу;
n общий срок займа;
i – проценты по депозиту.
Глава 3.2. Планирование погасительного фонда
Если по условиям займа должник обязуется вернуть сумму
долга в конце срока в виде разового платежа, то для накопления
таковой суммы обычно создается погасительный фонд.
Погасительный фонд создается из последовательных взносов должника, на которые начисляются проценты.
В обозначениях мы ввели две процентные ставки: i – определяет темп роста погасительного фонда; g определяет сумму
выплачиваемых за заем процентов. Очевидно, что сумма взносов
в фонд вместе с начисленными процентами, накопленная к концу
срока долга, должна быть равна его сумме.
21
Рассмотрим случай формирования фонда, когда взносы регулярны и одинаковы по величине и вносятся в конце года, т. е.
речь идет о годовой ренте постнумерандо. И вот тут нам необходимо пояснить, что это означает, хотя в первой лекции мы такое
понятие уже вводили.
Рента обычная, или постнумерандо, если платежи производятся в конце периода; рента пренумерандо, если платежи производятся в начале периода.
Выясним для начала, как вычисляется наращенная сумма
ренты постнумерандо.
Итак, наращенная сумма – сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Рассмотрим характеристики годовой ренты постнумерандо:
член ренты R – регулярный ежегодный взнос,
срок ренты n,
ставка i,
число выплат в году p=1,
число начислений процентов в году m=1.
Положим n=4 года и выведем формулу наращенной суммы
ренты.
Построим схему наращения членов ренты на временной
оси. Т. к. срок ренты больше одного года, естественно, следует
использовать сложные проценты.
Например, на член ренты R, внесенный в конце первого года, будут начисляться проценты 3 года. К концу срока ренты эта
сумма будет составлять R (1 i)3 .
Подобным образом на член ренты R, внесенный в конце второго года, будут начисляться проценты 2 года. К концу срока ренты
эта сумма будет составлять R (1 i)2 . И т. д., см. рисунок 3.1.
R
R
R
R
t
1
2
3
4
R(1+i)3
R(1+i)2
R(1+i)1
Рисунок 3.1.
22
По определению наращенной суммы ренты
S R (1 i)3
R
R (1 i) 2
R (1 i)1 R
R (1 (1 i) (1 i) 2
(1 i)3 )
(1 i)3 (1 i) 1
(1 i) 4 1
R
.
1 i 1
i
Но мы здесь рассматривали случай срока платежей – 4 года,
тогда в общем виде при n годах в этой формуле в числителе суммы (1+i) будет показатель степени, равный n.
Ввиду того, что кредит – это один из видов ренты, то
накопленная к концу срока фонда сумма долга D с процентами
есть наращенная сумма ренты S, равная
S D R
(1 i) n 1
.
i
(3.1)
Обозначим множитель наращения ренты через
S n,i
(1 i) n 1
,
i
тогда из формул 3.1 и 3.2 следует, что член ренты R
(3.2)
D
и
Sn ,i
в фонд систематически вносится сумма
Y Dg
D
.
Sn ,i
(3.3)
Величину процентного платежа I t , исчисленного по сложным процентам, вычисляют по формуле:
I t D (1 g) t 1 g , где t 1,2,…,n.
(3.4)
Пусть вас не пугают в этих формулах новые обозначения,
главное здесь сохраняется основная суть – сложные проценты.
Если условия контракта предусматривают присоединение
процентов к сумме основного долга по ставке g, то срочная уплата будет равна
Y
D (1 g ) n
.
S n ,i
(3.5)
Для расчета накопленных за t лет сумм погасительного фонда
используется формула наращенных сумм постоянных рент:
S t 1 S t (1 i) R .
(3.6)
23
Мы не рассматриваем здесь подробный вывод последних
формул, считая, что это усложнит курс, а потому просим принять
их без вывода.
Сделаем дополнительные пояснения по поводу создания
погасительного фонда.
Во-первых, это выгодно должнику только тогда, когда i g.
В этом случае должник на накопленные в погасительном фонде
средства получает больше процентов, чем сам выплачивает за заем. Причем, чем больше разность i g, тем больше экономия
средств должника, направляемая на покрытие долга.
Если i g, то преимущества создания фонда пропадают. В
этом случае финансовые результаты должника оказываются такими же, как и при погашении долга частями (о чем будем вести
речь позднее).
Задача 3.1
Для приобретения бытовой техники вы взяли кредит суммой 100 тыс. руб. на 5 лет под ставку g = 20%. Для его погашения
создается фонд. На инвестируемые средства начисляются проценты по ставке i = 22%. Необходимо найти размеры срочных
уплат. Взносы производятся в конце каждого года равными суммами.
Решение.
Итак, для решения задачи необходимо знать формулу 3.5
срочной уплаты Y
D (1 g ) n
.
S n ,i
Что нам известно из нее? Мы знаем из нее сумму долга D = 100 тыс. руб.; срок платежа n = 5 годам; ставку процентов по
займу g = 20%; проценты по депозиту i = 22%. Но нам неизвестен
множитель наращения Sn ,i , который мы найдем по формуле 3.2.
Приступим к его вычислению.
S n ,i
(1 i) n
i
1
(1 0,22) 5 1
7,7396.
0,22
24
Если проценты присоединяются к сумме долга, то срочная
уплата по формуле 3.5 будет равна
Y
D (1 g) n
Sn ,i
100 (1 0,2) 5
7,7396
32,1505 тыс. руб.
Если проценты не присоединяются к сумме долга, то ежегодные взносы в банк R
D
Sn ,i
100
12,9206 тыс.руб.
7,7396
Глава 3.3. Погашение долга в рассрочку
Метод погашения долга в рассрочку частями называется
амортизацией долга. Рассмотрим 2 способа погашения долга в
рассрочку.
Первый способ. Погашение основного долга равными суммами
Пусть долг D погашается в течение n лет, тогда сумма,
идущая на погашение долга равна
D
.
n
(3.7)
Размер долга уменьшается, и остатки долга соответственно
равны:
D; D
D
2D
3D
;D
;D
;…
n
n
n
Т. к. проценты начисляются на непогашенный остаток долга, то они также уменьшаются.
Пусть проценты выплачиваются один раз в году по ставке g.
Процентные платежи по годам соответственно равны:
D g; (D
D
2D
3D
) g; (D
) g; (D
) g;…
n
n
n
(3.8)
Обозначим суммы выплаченных процентов буквой J, тогда
она будет равна:
J
1
2
n 1
) (1
) … (1
))
n
n
n
n 1
1 (1
)
n 1
n
Dg
n Dg
.
2
2
Dg (1 (1
25
(3.9)
При выводе этой формулы мы используем формулу суммы
n-членов арифметической прогрессии Sn
a1 a n
n (в ней a 1 и a n
2
соответственно первый и последний члены , n – число членов
прогрессии).
Общая сумма погашения кредита будет складываться из
основного долга D и выплаченных процентов J, т. е. с применением формулы 3.9, получим:
S D J
D Dg
n 1
n 1
D (1 g
).
2
2
(3.10)
Если взносы в погашение кредита будут осуществляться
«р» раз в году, то общая сумма выплаченных процентов будет
равна,
D n p 1
g
.
p
2
J
(3.11)
Задача 3.2
Долг 1000 тыс. руб. необходимо погасить последовательными равными суммами за 5 лет платежами постнумерандо. За
заем выплачиваются проценты по годовой ставке 10%. Составить
план погашения кредита.
Решение.
Итак, долг D = 1 000 тыс. руб., ежегодная выплата долга по
формуле 3.7 будет равна
D
n
D
5
200 тыс. руб.
Найдем в соответствии с формулой 3.8 выплаченные проценты за 1-й год: J 1 1000 0,1 100 тыс. руб.;
Выплаченные
год J 2
проценты
(1000 200) 0,1 80 тыс. руб. и т. д.
за
2-й
За три последующих года вычислите выплаченные проценты самостоятельно и сверьте ваш результат с результатом, который мы представили в виде таблицы 3.1.
26
Таблица 3.1
Год
Остаток долга на
начало года
(тыс. руб.)
1
2
3
4
5
Итого
1 000
800
600
400
200
Расходы
по займу
Y = R+I
(тыс. руб.)
300
280
260
240
220
1300
Погашение
основного
долга R
(тыс. руб.)
200
200
200
200
200
1000
Проценты I
(тыс. руб.)
100
80
60
40
20
300
Основной недостаток такого расчета погашения долга –
большие платежи в начале выплат.
Далее рассмотрим второй способ погашения долга.
Второй способ. Погашение долга равными
срочными выплатами
По этому способу расходы должника по обслуживанию
долга постоянны на протяжении всего срока его погашения.
Из общей суммы расходов должника часть выделяется на
уплату процентов, остаток идет на погашение основного долга.
Периодическая выплата постоянной суммы Y = R равнозначна
ренте с заданными параметрами. Ее современная стоимость A
равна сумме долга D, т. е.
A
D R
1 (1 g)
g
n
.
(3.12)
В формуле 3.12 второй сомножитель назовем коэффициентом приведения годовой ренты со ставкой процентов g и сроком
n, и обозначим его
1 (1 g) n
.
g
D
Тогда расход по займу R Y
,
a n ,g
a n ,g
(3.13)
(3.14)
а сумма первого взноса по погашению основного долга будет задаваться формулой d 1 Y Dg.
(3.15)
27
Задача 3.3
Долг 1 000 тыс. руб. погашается в течение 5 лет платежами
постнумерандо по ставке g = 10%. Составить план погашения
кредита равными срочными выплатами с начислением процентов
на непогашенный остаток.
Решение.
Рассчитаем по формуле 3.14 расход по займу R = Y.
R
Y
D
a n ,g
1000
1 (1 g )
0,1
5
263,797 тыс. руб.
Первая выплата основного долга d1 = 263,797 – 1 000 0,1 =
= 163,797 тыс. руб.;
остаток долга D1 = 1 000 – 163,797 = 836,203 тыс. руб.;
Вторая выплата основного долга d2 = 263,797 – 836,203 0,1 =
=180,177 тыс. руб. и т. д.
Расчеты по оставшимся трем выплатам погашения долга и по
строке «Итого» предлагаем провести самостоятельно и результат
сверить с тем, который мы представляем в виде таблицы 3.2.
Таблица 3.2
Год
Остаток долга
на начало года
(тыс. руб.)
Расходы по займу Y
(тыс. руб.)
Проценты I
(тыс. руб.)
1
2
3
4
5
Итого
1 000
836,203
656,026
457,831
239,816
263,797
263,797
263,797
263,797
263,797
?
100,00
83,620
65,603
45,783
23,982
?
Погашение
основного
долга R
(тыс. руб.)
163,797
180,177
198,195
218,014
239,816
?
Итак, если ваши расчеты совпали с таблицей 3.2, то мы вас
поздравляем с составленным планом погашения кредита.
Что можно сказать по поводу получившейся таблицы, а
точнее, по поводу столбца проценты?
Вы замечаете, что при таком погашении долга процентные
платежи уменьшаются во времени, а сумма погашения основного
28
долга увеличивается, расходы по займу остаются постоянными на
весь срок, однако в этом случае должник немного переплачивает.
Какую суммы он переплачивает – это еще одна задачка, которую
вы должны решить самостоятельно.
Ну а мы перейдем к рассмотрению погашения потребительского кредита.
Глава 3.4. Погашение потребительского кредита
В потребительском кредите проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному
долгу уже в момент открытия кредита, т. е. разовым начислением
процентов.
Величина разового погасительного платежа определяется
формулой
Y
D (1 ng )
,
np
(3.16)
где
n – срок кредита в годах,
p – число платежей в году.
Для решения проблемы определения остатка задолженности на любой момент времени следует разбить величину Y на
проценты и сумму, идущую на погашение основного долга.
И снова рассмотрим возможность такового разбиения двумя способами.
Первый способ: равномерное распределение выплаты
процентов.
Величину разового платежа Y, см. формулу 3.16, представим в виде суммы (мы выполняем почленное деление на знаменатель дроби):
Y
D
np
D g
p
R I,
(3.17)
где
D – цена товара (сумма основного долга без процентов);
R – размер погашения основного долга;
I – процентный платеж.
29
Замечание:
В случае срока кредита больше года применяются сложные
проценты. Тогда процентный платеж будет определяться формулой:
(3.18)
I D ((1 g) n 1) .
Второй способ: правило 78.
Естественно, возникает вопрос: «С чем связано название
этого правила, почему именно 78, а не что-то другое?»
А все очень просто. Дело в том, что сумма порядковых номеров месяцев в году равна 78, отсюда и название правила. Чтобы убедиться в этом, можно, конечно, сложить натуральный ряд
чисел от 1 до 12. А можно вспомнить о великом математике Карле Гауссе, который не складывал натуральный ряд чисел от 1 до
100, а просто вывел формулу суммы членов арифметической прогрессии (мы к ней уже обращались при выводе формулы 3.9).
Предлагаем вам в этом убедиться, и тогда вы уж точно не забудете, почему один из способов погашения потребительского кредита называется правилом 78.
Допустим, что срок кредита равен 1 году. Тогда, согласно
правилу 78, доля процентов в сумме расходов в первом месяце
равна 12/78, во втором она составит 11/78 и т. д. Последняя уплата процентов равна 1/78.
Таким образом, доля процентов убывает, сумма погашения
основного долга увеличивается.
Для годового срока процент погашения и сумма основного
долга соответственно задаются формулами:
t
D g.
78
D (1 g)
R Y I
12
(3.19)
I
t
D g.
78
(3.20)
Задача 3.4
Вы закончили РФЭИ, и вас взяли на работу в отдел кредитования одного из филиалов Сбербанка в вашем городе или поселке с испытательным сроком три месяца. Естественно, с первых дней вы только осваиваете работу специалиста этого отдела,
наблюдая за работой других. Вы – только стажер. Но буквально
30
через неделю вашей «практики» руководитель отдела кредитования предлагает вам оформить клиенту потребительский кредит
по правилу 78. Клиент пришел в банк за помощью, зная, что банк
выдает потребительские кредиты по ставке 20% годовых. Его пока интересуют условия, план погашения и т. д. Он намерен оформить кредит в размере 240 тыс. руб. сроком на 1 год. У руководства есть возможность проверить ваши профессиональные качества. Причем эту работу вам предлагают сделать в тот самый неподходящий момент, когда банковская система временно вышла
из строя, компьютеры не работают, и у вас нет возможности воспользоваться компьютерной программой. Но на вашем рабочем
столе калькулятор и с вами ваши знания.
Итак, за работу.
Решение.
Клиент сидит перед вами, и вы ему объясняете, что общая
сумма задолженности будет равна S = 240(1+0,2) = 288 тыс. руб.
Общая сумма выплаченных процентов будет равна разности
I = 288 – 240 = 48 тыс. руб.
Ежемесячная выплата (сумма расходов по обслуживанию
долга будет равна)
Y
S
n
288
12
24 тыс. руб.
Вы ему объясните, что процентные платежи по месяцам и
основной долг будут такими:
для первого месяца они соответственно равны
I1
12
48 7,385 тыс. руб.; R 1
78
24 7,385 16,615 тыс. руб.
Для второго месяца:
I2
11
48 6,769 тыс. руб.; R 2
78
24 6,769 17,231 тыс. руб.
и т. д.
Оставшуюся часть работы вы выполняете без нас (самостоятельно). Но мы просчитаем вместе с вами только последний, 12й месяц года
I12
1
48 0,615 тыс. руб.;
78
31
24 0,615 23,385 тыс. руб.
R 12
Как вы себя можете проверить?
Сложением получившихся результатов. Если их сумма будет составлять 288 тысяч рублей, вы работу выполнили правильно. Клиент остался доволен вашими разъяснениями. Руководитель отдела кредитования доволен стажером, который, несмотря
на технические проблемы (отсутствие компьютерной связи), не
отпустил клиента, а привлек его, сформировав полностью план
погашения кредита. Вы повысили свою вероятность быть принятым специалистом в отдел кредитования банка.
Ну а мы, прежде чем двигаться дальше, хотели бы, чтобы
вы мысленно для себя прокомментировали: почему, на основании
каких формул мы поступали так, а не иначе, при составлении
плана погашения задолженности по кредиту.
А теперь мы обобщим правило 78 для кредита со сроком N
месяцев.
Последовательные номера месяцев в обратном порядке
представляют собой числа:
t = N, N-1,…, 1.
(Мы обозначили последовательные номера месяцев латинской буквой «N», т. к. «n» уже нами используется). Вспомните,
какую роль она выполняет в финансовых расчетах. Да, она определяет срок (продолжительность) кредита.
А теперь сумму этих чисел находим по формуле известной
вам суммы арифметической прогрессии:
N
t
1
(1 N)
N.
2
Тогда ежемесячные выплаты процентов в соответствии с
формулой 3.19 будут равны
I
t
t
D g n.
(3.21)
Сумма списания основного долга будет определяться формулой:
R
Y
t
t
32
D g n.
(3.22)
В каждом месяце выплаты процентов сокращаются на величину
D g n
, на такую же величину увеличивается сумма спиt
сания основного долга.
Важно отметить, что в потребительском кредите при разовом
начислении процентов должник фактически выплачивает проценты
и за описанные суммы долга. Это значит, кредит обошелся бы дешевле, если бы проценты начислялись на остатки долга.
Применим наши теоретические рассуждения к практической ситуации.
Задача 3.5
Потребительский кредит в сумме 10 млн. руб. выдан на три
года при разовом начислении процентов по ставке 10% годовых.
Погашение задолженности помесячное.
Составить амортизационные планы погашения кредита:
a) по правилу 78;
б) по методу равномерного распределения выплат процентов.
Решение.
а) по правилу 78:
Общая сумма долга S 10 (1 3 0,1) 13 млн. руб.
Итак, переплата будет составлять 3 млн. руб.
А теперь посмотрим, как эта сумма будет распределяться.
Сумма расходов по обслуживанию долга будет найдена как
S 13
0,361111 млн. руб. 361,111 тыс. руб.
n 12 3
Y
Сумма последовательных номеров месяцев будет определяться по формуле суммы арифметической прогрессии, и расположим месяцы в обратном порядке.
36
t
1
1
2
30 31 32 33 34 35 36
(1 36)
36 666; t 36, 35,…, 7, 6, 5, 4, 3, 2, 1 .
2
Рассчитаем процентные платежи I и суммы погашения основного долга R в соответствии с формулами 3.21 и 3.22.
Для 1-го месяца t = 36, и поэтому получаем
I
36
3 0,162162 млн. руб. 162,162 тыс. руб. ;
666
33
R 361,111 162,162 198,949 тыс. руб.
Для 2-го месяца в числителе уже значение t = 35, тогда
35
3 0,157658 млн. руб. 157,658 тыс. руб. ;
666
R 361,111 157,658 203,453 тыс. руб.
I
Далее найдем процентные платежи I и суммы погашения
основного долга R для 30-го месяца:
7
3 0,031532 млн. руб 31,532 тыс. руб. ;
666
R 361,111 31,532 329,579 тыс. руб.
I
Опустив расчет еще ряда промежуточных платежей,
найдем аналогичные показатели для 36-го месяца:
1
3 0,004505 млн. руб 4,505 тыс. руб. ;
666
R 361,111 4,505 356,606 тыс. руб.
I
Насколько верно вы составили план погашения кредита,
ответит элементарная математическая проверка. В чем ее суть?
Общая сумма процентных платежей (суммирование по I) должна
дать 3 млн. руб., а общая сумма выплат основного долга (суммирование по R) должна дать 10 млн. руб.
б) по методу равномерного распределения выплат процентов
Величину разового платежа Y по формуле 3.17 представим
в виде суммы
Y
D
pn
D g
p
R I , где
ежемесячная выплата основного долга
R
D
pn
10
12 3
10
36
0,277778 млн. руб. 277,778 тыс. руб. ,
ежемесячная выплата процентного платежа
I
D g
p
10 0,1
0,083333 млн. руб. 83,333 тыс. руб.
12
Проверку выполненных расчетов можно выполнить умножением каждого из вычисленных показателей на количество месяцев, в нашем случае на 36. Сумма получившихся произведений
должна дать 13 млн. руб. Проверьте и убедитесь. Расчет верен.
34
Итак, подводя итог рассмотренному материалу в последней
главе нашего курса, отмечаем, что за рассмотрением теоретической части следует выполнение практических работ.
Все практические задания будут сопровождаться ссылкой на
разделы и главы лекционного курса. Будьте внимательны, у вас
все непременно получится.
Конец курса
Все замечания и предложения отсылайте по адресу: [email protected]
35

Объединение платежей и эквивалентные платежи

Краткая теория

---

Принцип эквивалентности применяется при различных изменениях
условий выплат денежных сумм. Общий метод решения подобного рода задач заключается
в разработке так называемого уравнения эквивалентности, в котором сумма
заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается
к сумме платежей по новому обязательству, приведенных к той же дате. Для
краткосрочных обязательств приведение осуществляется обычно на основе

простых ставок,
для средне- и долгосрочных — с помощью

сложных ставок. Заметим, что в
простых случаях конверсии платежей часто можно обойтись без специальной разработки и решения
уравнения эквивалентности.

Одним из распространенных случаев изменения условия выплат является объединение платежей. 
Пусть платежи

 со сроками

 заменяются одним в сумме

 и сроком

.
В этом случае возможны две постановки задачи: если задается срок

,
то находится сумма

 и наоборот, если задана сумма
консолидированного платежа

,
то определяется срок

.

 При
решении задачи определения суммы консолидированного платежа уравнение
эквивалентности имеет простой вид. В общем случае, когда

,
причем

,
искомую величину находим как сумму наращенных и дисконтированных платежей. При
применении простых процентных ставок, получим:

где

 – размеры объединяемых платежей со сроками

 – размеры платежей со сроками

В частном случае, когда

При объединении обязательств можно
применить и учетные ставки. В этом случае при условии, что все сроки выплат
пролонгируются, то есть

,  находим сумму наращенных по учетной ставке
платежей:

В общем случае имеем:

 и

 имеют тот же смысл, что и выше.

Объединение платежей можно осуществить и на основе сложных
ставок.  Для общего случая получим:

Рассмотрим теперь более общие случаи изменения условий
выплат, предусматриваемых в контрактах, для которых решение нельзя получить
простым суммированием приведенных на некоторую дату платежей. Когда некоторое количество платежей заменяется эквивалентными платежами, с другими сроками и суммами. И в таких случаях
решение основывается на принципе эквивалентности платежей до и после изменения
условий. Метод решения заключается в разработке упоминавшегося выше уравнения
эквивалентности.  Если приведение
платежей осуществляется на некоторую начальную дату, то получим следуюшие
уравнения эквивалентности в общем виде.

при использовании простых процентов:

при использовании сложных процентов:

где

 и

 – параметры заменяемых платежей,

 и

 – параметры эквивалентных им платежей.

Конкретный вид уравнения определяется
содержанием контрактов.

Примеры решения задач

---

Задача 1

По
условиям погашения краткосрочного кредита, полученного под 15% годовых 12
февраля, предприятие должно выплатить следующие суммы в три срока: 16 марта -30
тыс.руб., 10 мая – 26 тыс.руб. и 1 сентября – 18 тыс.руб. В связи с возникшими
обстоятельствами предприятие просит банк объединить три платежа и перенести
дату выплаты долга на 1 июля. Определить величину консолидированного платежа.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Величину
суммы консолидированного платежа можно найти по формуле:

 – размеры объединяемых платежей со сроками

 – размеры платежей со сроками

Подсчитаем
сроки платежей в днях (от 12.02):

Для
1-го платежа 16-го марта:

Для
2-го платежа 10 мая:

Для
3-го платежа 1 сентября:

Срок
консолидированного платеж 1 июля:

 

Ответ:

---

Задача 2

Замените
поток платежей – 70000 руб. – через 1 год, 120000 руб. – через 2 года, 90000
руб. – через 3 года – эквивалентным множеством, состоящим из двух выплат,
равных по величине: первая – через 1.5 года, вторая – через 4 года. Проценты
начисляются по ставке 8% годовых каждые 6 месяцев.

Решение

Если
приведение платежей осуществляется на некоторую начальную дату, то при получим
следующее уравнение эквивалентности:

Примем
в качестве базовой даты текущий момент. Уравнение эквивалентности в этом случае
запишется в следующем виде:

Решая
полученное уравнение, получаем:

Размер
платежа через 1.5 и 4 года равен 132337.1 руб.

Ответ:

 

Обновлено: 15.05.2023

В качестве метода, позволяющего осуществить принцип фи­нансовой эквивалентности обязательств, принято использовать метод приведения (с помощью операций дисконтирования и на­ращения) платежей к одному моменту времени.

При применении метода приведения прежде всего следует выбрать базовый момент времени – момент, к которому предпо­лагают привести все суммы в расчете.

Дисконтирование применяют, если необходимо привести пла­тежи к более ранней дате, наращение – если базовый момент времени относится к будущему.

Задача 16. Выясните, являются ли равноценными два обязательства, если по первому должно быть выплачено 2 млн р. через 2 года, по второ­му – 2,5 млн р. через 3 года. Для сравнения примените сложную процент­ную ставку 15 % годовых.

Решение. Дано FV₁=_________; n₁=______; FV₂=__________; n₂=______; i_c=________.

Для сравнения приведем каждый платеж к начальному моменту вре­мени.

Стоимость первого платежа в начальный момент составляла

Стоимость второго платежа в начальный момент

На практике при изменении условий платежей принцип фи­нансовой эквивалентности обязательств реализуют путем состав­ления уравнения эквивалентности, согласно которому сумма за­меняемых платежей, приведенных к одному моменту времени, приравнивается к сумме платежей по новому соглашению, приве­денных к тому же моменту времени. Для краткосрочных контрак­тов процесс приведения реализуют, как правило, на основе про­стых процентных ставок, для среднесрочных и долгосрочных кон­трактов – на основе сложных процентных ставок.

Задача 17. Имеются два кредитных обязательства 400 тыс. р. и 700 тыс. р. со сроками уплаты 1 августа 2010 г. и 1 января 2011 г. По согла­сованию сторон условия обязательств пересмотрены: первый платеж в раз­мере 600 тыс. р. должник вносит 1 ноября 20 Юг., остальной долг он выпла­чивает 1 марта 2011 г. Определите размер второго платежа, если в расче­тах используют простую процентную ставку 20 % годовых. Проценты точ­ные.

Задача 18.Согласно контракту предприятие должно выплатить 200, 300 и 500 тыс. р. соответственно через 1,5, 2 и 4 года. Предприятие предла­гает пересмотреть контракт и вернуть долг одним платежом через 3,5 года. Найдите размер консолидированного платежа, если применяется сложная процентная ставка 18 % годовых.

Задача 19.Вексель учтен в банке по простой учетной ставке 16% за 200 дней до срока его погашения. Временная база – 360 дней. Рассчитайте доходность этой финансовой операции в виде точной простой процентной ставки.

Задача 20. Ссуда выдана под сложную годовую процентную ставку 18%. Определите простую годовую процентную ставку, которая обеспечит эквивалентность финансовых результатов, если срок ссуды: 1) 3 года; 2) 3 месяца.

Задача 21. Какой сложной годовой процентной ставкой можно заменить в контракте простую годовую процентную ставку 19%, не изменяя финансовых отношений сторон, если срок финансовой операции 438 дней, а проценты точные?

Задача 22. Сравните два долговых обязательства. По первому обязательству следует выплатить 40000 р. через 4 месяца, по второ­му – 43000 р. через 8 месяцев. Можно ли считать эти обязатель­ства равноценными? Для сравнения примените простую годовую процентную ставку 15 %. При какой ставке сравнения эти платежи будут равноценными?

Задача 23. Два долговых обязательства на сумму 300 и 900 тыс. р. должны быть погашены соответственно через 2 года и через 5 лет. Стороны пришли к соглашению изменить порядок выплат: 200 тыс. р. выплачивают через 1 год, 500 тыс. р. – через 4 года, а остаток дол­га – через 6 лет. Определите размер третьего платежа, если в рас­четах используют сложную годовую процентную ставку 20%.

Задача 24. Три векселя на сумму 500, 800 и 900 тыс. р. со срока­ми уплаты 15 марта, 10 апреля и 1 июня соответственно заменяют одним платежом со сроком погашения 15 мая. Определите сумму консолидированного векселя, если при расчетах использована про­стая годовая учетная ставка 18%.

Задача 25. Платежи в размере 250, 310 и 270 тыс. р. должны быть внесены через 40, 70 и 160 дней соответственно. Стороны до­стигли соглашения заменить их одним платежом 825 тыс. р. Опре­делите срок уплаты консолидированного платежа, используя про­стую годовую процентную ставку 12 %. Проценты обыкновенные.

Домашняя работа

Задача 1. Определите значение простой годовой процентной ставки, эквивалентной простой годовой учетной ставке 16 %, для финансо­вой операции сроком на 2 месяца.

Задача 2. Найдите простую годовую учетную ставку, эквивалентную простой годовой процентной ставке 16 %, при наращении капитала:а) за 1 год; б) за 2 года; в) за 120 дней. Временные базы обеих ставок составляют 360 дней.

Задача 3. Требуется определить доходность векселя в пересчете на простую точную процентную ставку, если учетная ставка равна 15 % при временной базе 360 дней, а срок уплаты по векселю насту­пит через 80 дней.

Задача 4. Финансовая операция сроком 65 дней должна принести 14 % дохода в виде простых точных процентов (в расчете на год). Какую простую обыкновенную учетную ставку для этого необходимо на­значить?

Задача 5. Какой сложной годовой процентной ставкой можно заме­нить в контракте простую годовую точную процентную ставку 21%, не изменяя финансовых отношений сторон? Срок операции — 710 дней.

Задача 6. Ссуда выдана под сложную годовую процентную ставку 18 %. Рассчитайте, какая простая процентная ставка обеспечит такой же финансовый результат, если срок ссуды: а) 5 лет; б) 6 месяцев.

Задача 7. Платеж в сумме 5 тыс. р. со сроком уплаты 4 месяца требует­ся заменить платежом со сроком уплаты: а) 3 месяца; б) 6 месяцев. Определите сумму платежа, если при расчетах используют простую годовую процентную ставку 10 %.

Задача 8. Платеж в сумме 10 тыс. р. со сроком уплаты 4 месяца за­менили платежом 10,2 тыс. р. Определите срок этого платежа, если при расчетах используют простую годовую процентную ставку 10 %.

Задача 9. Платеж в сумме 60 тыс. р. со сроком уплаты 4 года требуется заменить платежом со сроком: а) 2 года; б) 5 лет. Определите сумму платежа, если при расчетах используют сложную годовую процент­ную ставку 12 %.

Задача 10. По условиям финансового обязательства фирма должна через 1 год выплатить 185 тыс. р. Кредитор не возражает против оплаты этого обязательства через 1,5 года, но в большей сумме — 200 тыс. р. Какой вариант погашения долга целесообразно избрать, если на рынке финансовых инструментов аналогичной срочности сложилась годовая процентная ставка 14 %.

Задача 11. Платеж в сумме 25 тыс. р. со сроком уплаты 180 дней пред­лагается заменить: а) платежом 24 тыс. р.; б) платежом 27 тыс. р. Определите срок нового платежа, если в расчетах используют про­стую процентную ставку 15 % и начисляют обыкновенные проценты.

Задача 12. Платеж в сумме 50 тыс. р. со сроком уплаты 60 дней требу­ется заменить платежом со сроком уплаты: а) 45 дней; б) 80 дней. Определите суммы новых платежей, если в расчетах применяют простую учетную ставку 19 % и обыкновенные проценты.

Задача 13. Платеж в сумме 150 тыс. р. со сроком уплаты 45 дней пред­лагается заменить платежом 175 тыс. р. Определите срок нового платежа, если при расчетах применяли простую учетную ставку 12%, а временная база — 360 дней.

Задача 14. Два платежа в сумме 100 тыс. р. и 50 тыс. р. со сроками упла­ты соответственно 150 и 180 дней объединяют в один со сроком уплаты 200 дней. Стороны согласились на применение простой го­довой процентной ставки, равной 10 %. Проценты точные. Найдите сумму консолидированного долга.

Задача 15. Платежи в сумме 100 тыс. р. и 200 тыс. р. со сроками упла­ты соответственно 2 и 3 года объединяют в один платеж со сроком уплаты 2,5 года. При консолидации платежей используют слож­ную ставку 18%. Определите сумму консолидированного плате­жа.

Задача 16. Фирма для погашения задолженности банку за предостав­ленный под 15% годовых (проценты простые, точные) кредит, по­лученный 5 января, должна осуществить три платежа — 200, 270 и 330 тыс. р. в сроки 24 апреля, 29 мая и 19 июня. Фирма предложила банку объединить все платежи в один и погасить его 5 июня. Опре­делите размер консолидированного платежа.

Задача 17. Объединяют три платежа со сроками 20 мая, 20 июня и 20 ав­густа текущего года и суммами 100, 200 и 150 тыс. р. соответственно. Единый платеж должен быть совершен 6 августа. Определите сум­му консолидированного платежа, если при расчетах используют простую точную годовую процентную ставку 12%.

Задача 18. Два векселя на сумму 10 тыс. и 20 тыс. р. со сроками погашения июня и 1 августа соответственно заменяют одним векселем с прод­лением срока до 1 октября. Определите сумму нового векселя, если при объединении применена простая годовая учетная ставка 8 %.

Задача 19. Должник обратился к своему кредитору (владельцу векселя) с просьбой об объединении двух векселей в один с одновременным продлением срока оплаты. Первый вексель выдан на сумму 150 тыс. р. со сроком уплаты 20 июля, второй — на сумму 210 тыс. р. со сроком уплаты 1 сентября. Владелец векселя согласился на отсрочку пога­шения долга до 1 октября. Определите сумму к погашению, если при расчетах применяли простую годовую учетную ставку 10%, а временная база — 360 дней.

Задача 20. Имеются два кредитных обязательства 50 тыс. р. со сроком уплаты 1 октября текущего года и 70 тыс. р. со сроком уплаты 15 января следующего года. По согласованию сторон обязатель­ства пересмотрены на следующих условиях: первый платеж в сумме 80 тыс. р. должник вносит 15 декабря текущего года, а осталь­ной долг он выплачивает 20 февраля следующего года. При расче­тах используют простую точную годовую процентную ставку 12 %. Необходимо определить сумму второго платежа.

Изменение хозяйственной ситуации нередко побуждает одну из сторон-участниц коммерческой сделки обратиться к другой стороне с предложением изменить условия ранее заключенных соглашений.

Наиболее часто предлагается: изменить сроки платежей в один (консолидировать платежи) с установлением единого срока погашения и т.п. Естественно, что предлагаемые изменения должны быть безубыточны для обеих сторон, т.е. основным принципом изменения условия сделки (контракта) является принцип финансовой эквивалентности. Для решения таких задач используется уравнение эквивалентности, в котором сумма заменяемых платежей, приведенных к одному моменту времени, приравнена к сумме платежей по новому обязательству, приведенной к той же дате.

При консолидации нескольких платежей в один при условии, что срок нового консолидированного платежа больше ранее установленных сроков, т.е. no >n1, n2, nj, уравнение эквивалентности имеет вид:

где So – наращенная сумма консолидированного платежа;

Si, S2. Sj – платежи, подлежащие консолидации, со сроками уплаты ni,

tj- временные интервалы между сроком no и nj, т.е. tj = no-nj.

Рассмотрим использование данного уравнения.

Задача. Фирма получила кредит на сумму 900тыс.руб под 10% годовых (простые проценты). Кредит должен быть погашен двумя платежами: первый – 500 тыс. руб. с процентами через 90 дней, второй – 400 тыс. руб. с процентами через 120 дней. Впоследствии фирма договорилась с кредитором об объединении платежей в один со сроком погашения через 150 дней. Необходимо определить размер консолидированного платежа (К=360). Суммы, подлежащие возврату на старых условиях:

Сумма погашения консолидированного платежа будет равна:

Так как принцип эквивалентности состоит в том, что первоначальная сумма Р в начале периода эквивалентна платежу S в конце периода, то дисконтированная сумма консолидированного платежа на момент предоставления кредита должна быть равна сумме полученного кредита:

Объединение платежей может производиться на условиях, предусматривающих разные сроки выплаты консолидированного платежа.

Поэтому в общем случае величину консолидированного платежа определяют по формуле:

где Sj- суммы объединенных платежей, сроки погашения которых меньше нового срока njП0

Соответственно, tj = П0-Пі, tk = nk-n0.

Задача. Фирма в погашение задолженности банку за предоставленный под 15% годовых (простые проценты) кредит, полученный 01.01, должна произвести три платежа – 200 тыс. руб.; 270 тыс. руб. и 330 тыс. руб. в сроки 20.04, 25.05, 15.06. Фирма предложила банку объединить все платежи в один и погасить его 01.06. (К=365)

Определите величину консолидированного платежа. ti = 20.04 – 01.06= 42 дня, t₂ = 7 дней, t₃= 14 дней.

При консолидации платежей с использованием сложной процентной

ставки применяется следующая формула-

Задача. Два платежа S_t= 1,7 млн руб и S₂= 1,3 млн руб. со сроками погашения 1 год 30 дней и 1 год 45 дней, отсчитываемыми от одной даты, заменяются одним платежом со сроком 1 год 75 дней. Стороны согласились на консолидацию платежей при использовании ставки сложных процентов 9% годовых. Определите сумму консолидированного платежа. (к=365) t_x = 1 год 75 дней – 1 год 30 дней = 45 дней. t₂= 1 год 75дней – 1 год 45 дней =30 дней.

Вопрос о консолидации платежей можно решить и по другому принципу: партнеры заранее обусловливают сумму консолидированного платежа, при этом необходимо рассчитать срок его уплаты, сохраняя при этом принцип эквивалентности, Срок уплаты консолидированного платежа определяется по формуле:

где S0- сумма консолидированного платежа;

Ро – современная величина консолидируемых платежей; i- процентная ставка, используемая при консолидации.

Задача. Фирма имеет ряд финансовых обязательств перед одним кредитором – 2,5 млн. руб, 3,1 млн руб, 2,7 млн руб, которые должна погасить через 40, 70 и 160 дней после 01.01 текущего года. По согласованию сторон решено заменить их одним платежом, равным 9 млн руб., с продлением срока оплаты, используя процентную ставку i=12%. (К=365) Необходимо найти срок уплаты консолидированного платежа.

Современная величина (Р0) объединяемых платежей составит:

В случае договоренности партнеров о консолидации платежей без изменения общей суммы платежа, т.е. S0=^ Sj, срок консолидированного платежа рассчитывается по формуле:

Задача. Платежи в размере 2,5 млн руб., 3,1 млн руб и 2,7 млн. руб. должны быть внесены 40, 70 и 160 дней после 01.01 текущего года. Достигнуто соглашение на объединение этих платежей без увеличения итоговой суммы, т.е. S0=£ Sj. Определите срок уплаты консолидированного платежа.

Две суммы денег ЕУ₁ и ЕУ₂, выплачиваемые в разные моменты времени, счи­таются эквивалентными, если их современные (или наращенные) величи­ны, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Общий метод решения задач подобного рода заклю­чается в разработке уравнения эквивалентности, в котором сумма заменя­емых платежей, приведенных к некоторому моменту времени, приравни­вается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных контрактов процесс приведения, как правило, реализуется на основе простых ставок, для среднесрочных и долгосроч­ных – на основе сложных.

Наиболее распространенным способом изменения условий контрак­тов является консолидация (объединение) и пролонгация (продление) фи­нансовых обязательств. Соответственно решаются две задачи:

1) при известных суммах платежей и их сроках, известном сроке кон­солидированного платежа, находится его сумма;

2) при известных суммах платежей и их сроках, известной сумме кон­солидированного платежа, находится срок его выплаты.

Простая процентная ставка. Для краткосрочных контрактов консо­лидация осуществляется на основе простых ставок. В случае консолиди­рования нескольких платежей в один сумма заменяемых платежей, приве­денных к одной и той же дате, приравнивается к новому обязательству:

ЕУ0 =Е ЕУт (1 + (П0 – Пт) • I) + £ ЕУ_Ч (1 + Ц – П0) • I) -1 ,

где ЕУ₀, п₀ – сумма и срок консолидированного платежа;

ЕУ_т – сумма объединенных платежей, сроки погашения которых меньше нового срока п_т п₀.

Пример 4.5. Фирма в погашение задолженности банку за предостав­ленный кредит 1 января 2011 под 15 % годовых (простые проценты), должна произвести три платежа – 200 ден. ед., 270 ден. ед, 330 ден. ед. в сроки 20.04.11, 25.05.11, 15.06.11. Фирма предложила объединить все пла­тежи в один и погасить его 01.06.11. Определить величину консолидиро­ванного платежа.

Решение. С учетом порядковых дней года (приложение А) имеем