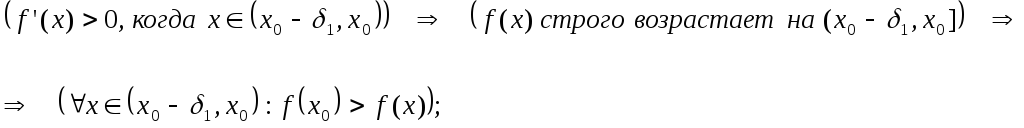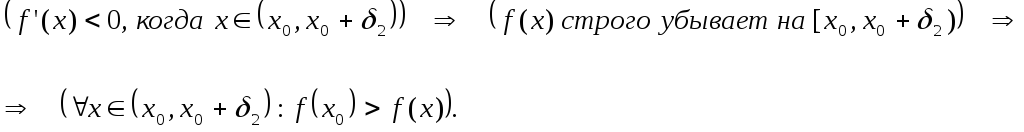Как найти стационарные точки для функции - Сайт, где вы сможете решить свои вопросы

Стационарные точки функции.
Необходимое условие локального
экстремума функции
Первое достаточное условие локального
экстремума
Второе и третье достаточные условия
локального экстремума
Наименьшее и наибольшее
значения функции на сегменте
Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1}_.Пусть функция определена на _{.

Точка}_{называется стационарной точкой функции}_,

если_{дифференцирована в точке}_и_.

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция определена на _{и имеет в точке}_{локальный экстремум. Тогда выполняется

одно из условий:}

функция _{не имеет в точке}_{производной;}
функция _{имеет в точке}_{производную и}_.

_{Таким образом, для того,

чтобы найти точки, которые являются

подозрительными на экстремум, надо

найти стационарные точки функции и

точки, в которых производная функции

не существует, но которые принадлежат

области определения функции.}

_Пример_{.

Пусть}_{.

Найти для нее точки, которые являются

подозрительными на экстремум. Для

решения поставленной задачи, в первую

очередь, найдем область определения

функции:}_{.

Найдем теперь производную функции:}

_{Точки, в которых производная

не существует:}_{.

Стационарные точки функции:}

_{Поскольку и}_,

и_{принадлежат области определения функции,

то они обе будут подозрительными на

экстремум. Но для того, чтобы сделать

вывод, будет ли там действительно

экстремум, надо применять достаточные

условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция определена на _{и дифференцирована на этом интервале

везде за исключением, возможно, точки}_{,

но в этой точке}_{функция}_{является

непрерывной}_{. Если

существуют такие правая и левая

полуокрестности точки}_{,

в каждой из которых}_{сохраняет определенный знак, то}

_{1) функция}_{имеет локальный экстремум в точке}_,

если_{принимает значения разных знаков в

соответствующих полуокрестностях;}

_{2) функция}_{не имеет локальный экстремум в точке}_{,

если справа и слева от точки}_{имеет одинаковый знак.}

_{Доказательство}_{.

1) Предположим, что в полуокрестности}_{производная}_{,

а в}_.

_{Таким образом в точке}_{функция}_{имеет локальный экстремум, а именно –

локальный максимум, что и нужно было

доказать.}

_{2) Предположим, что слева

и справа от точки}_{производная сохраняет свой знак,

например,}_{.

Тогда на}_и_{функция}_{строго монотонно возрастает, то есть:}

_{Таким образом экстремума

в точке}_{функция}_{не имеет, что и нужно было доказать.}

_{Замечание 1}_{.

Если производная}_{при прохождении через точку}_{меняет знак с «+» на «-», то в точке}_{функция}_{имеет локальный максимум, а если знак

меняется с «-» на «+», то локальный

минимум.}

_{Замечание 2}_{.

Важным является условие непрерывности

функции}_{в точке}_{.

Если это условие не выполняется, то

теорема 1 может не иметь места.}

_Пример_{.

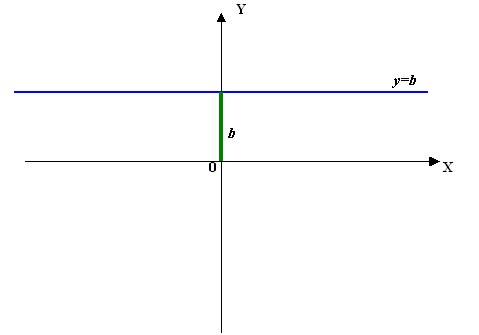
Рассматривается функция (рис.1):}

Эта функция определена на _{и непрерывна везде, кроме точки}_{,

где она имеет устранимый разрыв. При

прохождении через точку}_{меняет знак с «-» на «+», но локального

минимума в этой точке функция не имеет,

а имеет локальный максимум по определению.

Действительно, около точки}_{можно построить такую окрестность, что

для всех аргументов из этой окрестности

значения функции будут меньше, чем

значение}_{.

Теорема 1 не сработала потому, что в

точке}_{функция имела разрыв.}

_{Замечание 3}_{.

Первое достаточное условие локального

экстремума не может быть использовано,

когда производная функции}_{меняет свой знак в каждой левой и каждой

правой полуокрестности точки}_.

_Пример_{.

Рассматривается функция:}

_{Поскольку}_,

то_{,

а потому}_,

но_{.

Таким образом:}

_{т.е. в точке}_{функция}_{имеет локальный минимум по определению.

Посмотрим, сработает ли здесь первое

достаточное условие локального

экстремума.}

_Для_:

Для первого слагаемого правой
части полученной формулы имеем:

_{а потому в малой окрестности

точки}_{знак производной определяется знаком

второго слагаемого, то есть:}

_{а это означает, что в любой

окрестности точки}_{будет принимать как положительные, так

и отрицательные значения. Действительно,

рассмотрим произвольную окрестность

точки}_:_{.

Когда}

_то

_{(рис.2), а}_{меняет свой знак здесь бесконечно много

раз. Таким образом, нельзя использовать

в приведенном примере первое достаточное

условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

найти экстремумы функции

f(x)=x2x−1

Производная этой функции —

f′(x)=xx−2(x−1)2

, значит, критические точки функции — это (x=0) и (x=2). Точка (x=1) не принадлежит области определения функции.

Они делят реальную числовую прямую на четыре интервала:

−∞;0∪0;1∪1;2∪2;+∞

. Знак первого интервала положительный (например,

f′

((-1)=0.75)). Второго — отрицательный, третьего — отрицательный, четвёртого — положительный.

−∞;0	0;1	1;2	2;+∞
(+)	(-)	(-)	(+)

Значит, производная меняет знак только в точках (x=0) и (x=2).

В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).

В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).

Источник

Онлайн калькулятор для определения стационарных точек.
Стационарные точки – это точки, в которых производная функции равна 0 или не существует.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Как найти стационарные точки функции

Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Вам понадобится

– функция, которую необходимо исследовать на наличие стационарных точек;
– определение стационарных точек: стационарные точки функции – это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.

Инструкция

Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.

Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений – в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.

Обратите внимание

При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.

Полезный совет

Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.

Внимание и концентрация на задаче также помогут с ней справиться – перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.

Источники:

Производная функции – Википедия
Критическая точка (математика) – Википедия

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Содержание:

Критические точки и экстремумы функции
Теорема Ферма (Необходимое условие существовании экстремумов)
Достаточное условие существования экстремума
Задача пример №117
Задача пример №118
Задача пример №119
Задача пример №120
Задача пример №121

Критические точки и экстремумы функции

В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.

1. Для значений равных угловой коэффициент касательной к графику равен 0. Т.e. . Эти точки являются критическими точками функции.

2. В точках функция не имеет производной. Эти тоже критические точки функции.

3. Для рассматриваемой нами функции критические точки делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки – критические точки, которые не изменяют возрастание и убывание (или наоборот).

По графику видно, что в точках внутреннего экстремума производная функции равна нулю, а в точке производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.

Теорема Ферма (Необходимое условие существовании экстремумов)

Во внутренних точках экстремума производная либо равна нулю, либо не существует.

Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке производная функции равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума

Пусть функция непрерывна на промежутке и . Если является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:

1 ) слева от точки положительна, а справа – отрицательна, то точка является точкой максимума.

2) слева от отрицательна, а справа – положительна, то точка является точкой минимума

3) с каждой стороны от точки имеет одинаковые знаки, то точка не является точкой экстремума.

Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.

Соответствующие наибольшее и наименьшее значения функции на отрезке записываются как и .

Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.

Задача пример №117

Для функции определите максимумы и минимумы и схематично изобразите график.

Решение:

Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.

1. Производная функции:

2. Критические точки функции:

3. Точки и разбивают область определения функции на три промежутка.

Проверим знак на интервалах, выбрав пробные точки:

для интервала

Интервал Пробные точки

Знак Возрастание и убывание

При имеем . (-1;3) – максимум

При имеем (1;-1) – минимум

4. Используя полученные для функции данные и найдя координаты нескольких дополнительных точек, построим график функции.

Задача пример №118

Найдите наибольшее и наименьшее значение функции на отрезке [-1;2].

Решение:

Сначала найдем критические точки. Так как , то критические точки можно найти из уравнения . Критическая точка не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке и на концах отрезка.

Из этих значений наименьшее – 4, наибольшее 12. Таким образом:

Задача пример №119

Найдите экстремумы функции .

Решение:

1. Производная функции:

2. Критические точки: ,

3. Интервалы, на которые критические точки делят область определения функции:

Проверим знак на интервалах, выбрав пробные точки.

Для промежутка возьмем

Для промежутка (0; 1,5) возьмем

Для промежутка возьмем

Интервал

Пробные точки

Знак Возрастание-убывание

Используя полученную для функции информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами и касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.

• Функция на промежутке возрастает.

• Точка критическая точка функции , но не является экстремумом.

• Функция на промежутке [0; 1,5] возрастает.

• Функция на промежутке убывает.

•

Задача пример №120

Найдите экстремумы функции

Решение:

1. Производная

2. Критические точки: для этого надо решить уравнение или найти точки, в которых производная не существует. В точке функция не имеет конечной производной. Однако точка принадлежит области определения. Значит, точка является критической точкой функции.

3. Промежутки, на которые критическая точка делит область определения функции: и

Определим знак , выбрав пробные точки для каждого промежутка:

Для возьмем Для возьмем

Интервал Пробные точки

Знак

Возрастание-убывание

• Функция на промежутке убывает.

• Функция на промежутке возрастает.

•

Задача пример №121

По графику функции производной схематично изобразите график самой функции.

Решение:

Производная в точке равна нулю, а при отрицательна, значит, на интервале функция убывающая. При производная положительна, а это говорит о том, что функция на промежутке возрастает. Точкой перехода от возрастания к убыванию функции является точка . Соответствующий график представлен на рисунке.