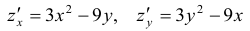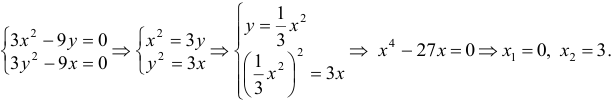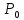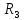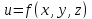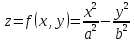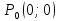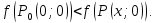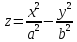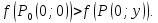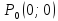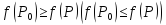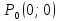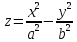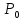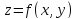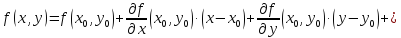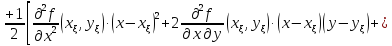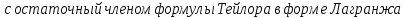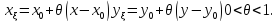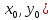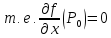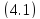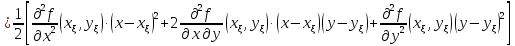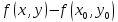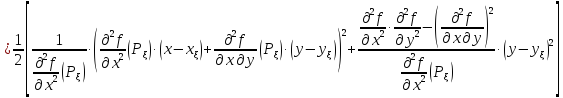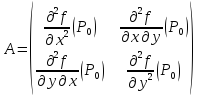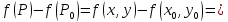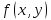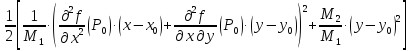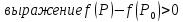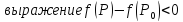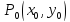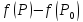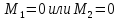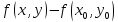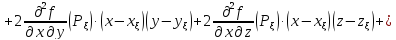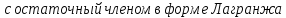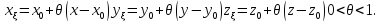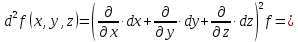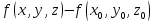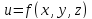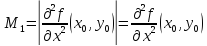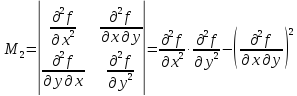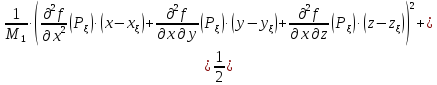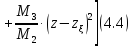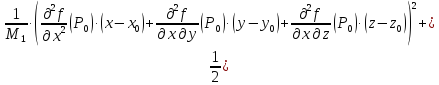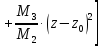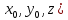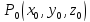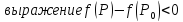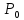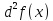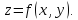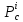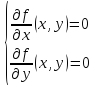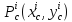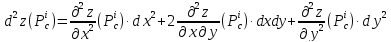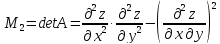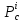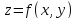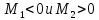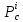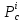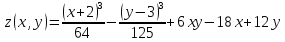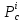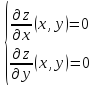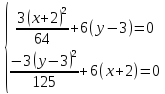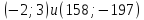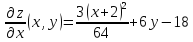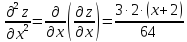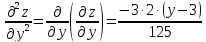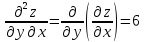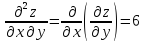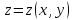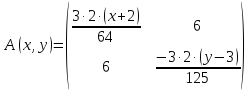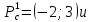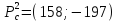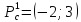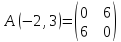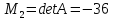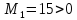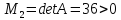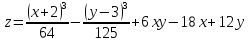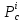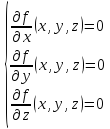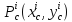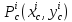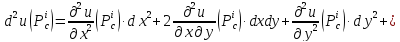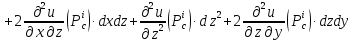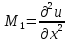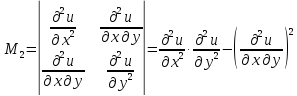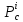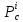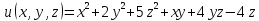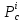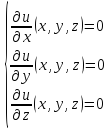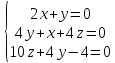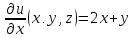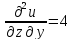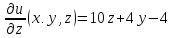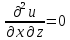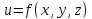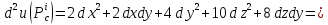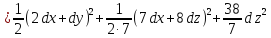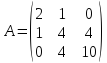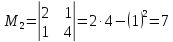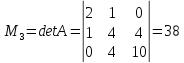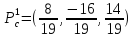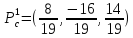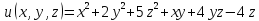Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.
Экстремум функции двух переменных
Как найти?
Постановка задачи
Найти экстремум функции двух переменных $ z = z(x,y) $
План решения
Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $
Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:
$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$
Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.
Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:
$$ A = z”_{xx} cdot z”_{yy} – (z”_{xy})^2 $$
Если в точке $ M(x_1,y_1) $:
- $ A>0 $ и $ z”_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
- $ A >0 $ и $ z”_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
- $ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
- $ A = 0 $, то требуется дополнительное исследование (по определению)
Итак, необходимо выполнить действия:
- Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
- Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
- Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $
Примеры решений
| Пример 1 |
| Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $ |
| Решение |
|
Находим частные производные первого порядка: $$ z’_x = 2x – y $$ $$ z’_y = -x + 2y $$ Приравниваем полученные выражения к нулю и решаем систему двух уравнений: $$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$ Решив систему получаем стационарную точку (подозрительные на экстремум): $$ M (0,0) $$ Далее вычисляем значения частных производных второго порядка в точке $ M $: $$ z”_{xx} Big |_M = 2 $$ $$ z”_{yy} Big |_M= 2 $$ $$ z”_{xy} Big |_M = -1 $$ Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков: $$ A = Big |_M = z”_{xx} Big |_M cdot z”_{yy} Big |_M – (z”_{xy} Big |_M)^2 = 2 cdot 2 – (-1)^2 = 3 $$ Так как получили $ A > 0 $ и $ z”_{xx} > 0 $, то получается $ M(0,0) $ точка минимума. Наименьшее значение находится в минимуме и равно: $$ z_{min} (0,0) = 0^2 – 0 cdot 0 + 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $ |
| Пример 2 |
| Найти экстремумы функции двух переменных $ z = x^3 + y^3 – 15xy $ |
| Решение |
|
Составляем систему уравнений из частных производных первого порядка: $$ begin{cases} z’_x = 3x^2 – 15y = 0 \ z’_y = 3y^2 – 15x =0 end{cases} $$ Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума. Вычисляем значение частных прозводных второго порядка в точке $ M_1 $: $$ z”_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$ $$ z”_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$ $$ z”_{xy} Big |_{M_1} = -15 $$ Подставляем данные значения в формулу достаточного условия экстремума: $$ A Big |_{M_1} = 0 cdot 0 – (-15)^2 = -225 $$ Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет. Получаем значения частных производных 2 порядка в $ M_2 $: $$ z”_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{xy} Big |_{M_2} = -15 $$ Вычисляем значение выражения достаточного условия экстремума: $$ A = 30 cdot 30 – (-15)^2 = 900 – 225 = 675 $$ Получили $ A > 0 $ и $ z”_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума. Наименьшее значение функции $ z = x^3 + y^3 – 15xy $ равно: $$ z_{min} |_{M_2} = 5^3 + 5^3 – 15 cdot 5 cdot 5 = 125 + 125 – 375 = -125 $$ |
| Ответ |
| В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $ |
Определение 1. Двумерной 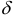
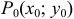
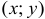
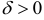
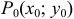
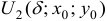
Если при фиксированном числе 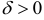
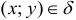
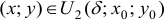
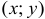
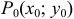
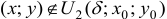
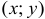
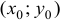
Если точка 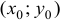
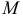
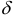
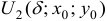
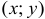
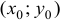
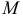
Определение 2. Точка 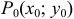
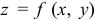
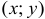
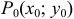
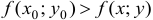
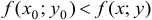
Значение функции 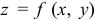
Если точка 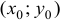
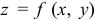
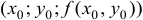
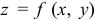
Слова «максимум» и «минимум» можно заменить одним «экстремум». Аналогично определяется экстремум функции трех и большего числа переменных.
Экстремум функции нескольких переменных может достигаться лишь в точках, лежащих внутри области ее определения, в которых все частные производные первого порядка обращаются в нуль. Такие точки называются стационарными. Для функции двух переменных 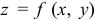
Условия (1) являются необходимыми условиями существования экстремума.
Достаточные условия экстремума для функции 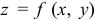
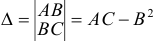
где 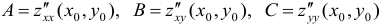
1) если 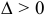
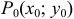
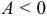
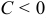
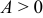
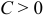
2) если 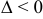
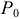
3) Если 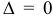
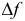
Пример №1
Найти экстремум функции 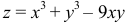
Решение:
1) Находим частные производные первого порядка
2) Воспользовавшись необходимыми условиями, находим стационарные точки
Из первого уравнения системы получим 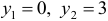
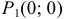
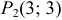
3) Находим частные производные второго порядка и их значения в стационарных точках: 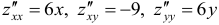
В точке 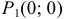
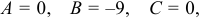
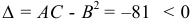
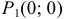
В точке 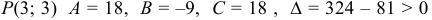
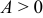
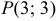
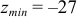
Пример №2
Исследовать функцию 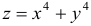
Решение:
Здесь стационарной точкой является (0; 0). В этой точке 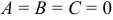
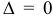
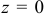
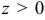
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Экстремум функции двух переменных. Примеры исследования функций на экстремум.
Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.
Точки максимума и минимума часто называют общим термином – точки экстремума.
Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.
Алгоритм исследования функции $z=f(x,y)$ на экстремум
- Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными. - Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
- Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$
Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:
$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$
Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.
$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$
Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$
Вычислим значение $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$
Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:
$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$
Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.
Пример №2
Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$
Сократим первое уравнение на 3, а второе – на 6.
$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$
Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:
$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$
Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):
$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$
Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:
begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}
Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:
$$Delta(M_1)=36(1^2-2^2)=-108.$$
Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.
Исследуем точку $M_2(-1;-2)$. В этой точке имеем:
$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$
Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.
Исследуем точку $M_3(2;1)$. В этой точке получим:
$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$
Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:
$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$
Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$
Исследование на экстремум завершено. Осталось лишь записать ответ.
Ответ:
- $(2;1)$ – точка минимума, $z_{min}=-27$;
- $(-2;-1)$ – точка максимума, $z_{max}=29$.
Примечание
Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 🙂
Пример №3
Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.
Решение
Будем следовать алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$
Сократим оба уравнения на $4$:
$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$
Добавим к второму уравнению первое и выразим $y$ через $x$:
$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$
Подставляя $y=-x$ в первое уравнение системы, будем иметь:
$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$
Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.
Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:
$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$
Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.
Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:
$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$
Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$
Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается “делайте, что хотите” :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$
В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.
Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$
Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.
Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.
Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.
Функции
нескольких переменных.
4.
Экстремум функции нескольких переменных.
Определение.
Точка
трех
( двух)-мерного пространства
(
) называется точкой локального максимума
(или минимума) функции нескольких
переменных
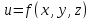
если существует такая её проколотая
окрестность, что для всех точек,
принадлежащих этой окрестности,
выполняется неравенство
Определение.
Точки
локального максимума и минимума
называются точками локального экстремума
функции.
Определение.
Значение
функции в точке локального экстремума
называется локальным экстремумом
функции.
Теорема
3.
(Необходимое условие экстремума ). В
точке локального экстремума
все частные производные первого порядка
равны нулю, если они существуют.
Следствие.
Если точка
является точкой локального экстремума
дифференцируемой в ней функции, то

Определение.
Точка, в которой все частные производные
функции
обращаются в нуль или не существуют,
называется критической точкой.
Определение.
Точка, в которой все частные производные
функции
обращаются в нуль, называется стационарной
точкой.
Замечание.
Стационарная точка может быть точкой
локального экстремума, а может и не быть
ею. Рассмотрим функцию двух переменных
(гиперболический
параболоид). Точка
является стационарной, т. к.
Рассмотрим
произвольную окрестность точки
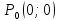
Возьмем два сечения окрестности
плоскостями Oxz
и Oyz
. В сечении первой плоскостью Oxz
( или

функция двух переменных
предстанет параболой
, ветви
которой направлены вверх и точка
является минимумом
В
сечении плоскостью Oyz
( или

функция двух переменных
предстанет параболой
, ветви
которой направлены вниз и точка
является максимумом
Следовательно,
для всех точек, принадлежащих окрестности
точки
ни одно из неравенств
не
выполняется. И
точка
не является ни максимумом , ни минимумом
функции
двух переменных
. Точки указанного типа называют точками
минимакса.
Пусть
функция
непрерывна вместе с частными производными
до второго порядка включительно в
окрестности стационарной точки
Определим условия, при которых
стационарная точка
будет являться точкой локального
экстремума функции
.
Формула
Тейлора для функции двух переменных
имеет вид
Здесь
Учитывая,
что точка
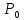
стационарная точка
(

из формулы Тейлора получаем, что знак
разности
определяется знаком выражения стоящего
в скобках.
Для
определения знака разности
преобразуем
последнее выражение, выделяя полный
квадрат
(4.2)
Замечание:
проверить правильность формулы (4.2)
раскрытием скобок.
Учитывая,
что дифференциал второго порядка для
функции двух переменных определяется
формулой
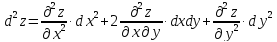
которая
имеет ту же структуру, что и выражение
в скобках(4.1),
можно сказать, что
знак выражения
совпадает со знаком дифференциала
второго порядка.
Дифференциалу
второго порядка можно поставить в
соответствие матрицу A
главные
миноры, которой
и

Тогда
выражение (4.2)
можно представить в более компактной
записи
Так
как по условию частные производные
второго порядка функции
непрерывны, то знак выражения
будет
иметь место и в некоторой окрестности
точки
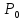
или
совпадать со знаком выражения (4.2).
При
этом получаем, что
1.
если

то
для
всех точек

принадлежащих проколотой окрестности
точки
и,
следовательно, точка

точка локального минимума.
2.
если
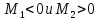
то
для
всех точек

принадлежащих проколотой окрестности
точки
и,
следовательно, точка
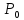
точка локального максимума.
3.
в случаях
знак выражения
непостоянен и,
следовательно, точка

точка не является ни минимум, ни максимумом
.
4.
если
, точка

точка может быть или не быть точкой
минимума или максимума. В этом случае
требуются дополнительные исследования.
Для
функции трех переменных
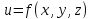
учитывая,
что точка
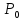
стационарная точка (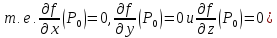
из формулы Тейлора получаем, что знак
разности
определяется знаком выражения стоящего
в скобках.
Здесь
формула
Тейлора для функции трех переменных
записана
Для
определения знака разности
преобразуем
последнее выражение, выделяя полные
квадраты
Учитывая,
что дифференциал второго порядка для
функции трех переменных определяется
формулой
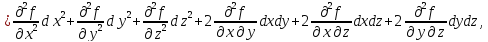
которая
имеет ту же структуру, что и выражение
в скобках(4.3),
можно сказать, что
знак выражения
совпадает со знаком дифференциала
второго порядка.
Полному
второму
дифференциалу функции
соответствует
матрица
Главные
миноры, которой
Тогда
выражение (4.3)
можно представить в более компактной
записи
Так
как по условию частные производные
второго порядка функции
непрерывны, то знак выражения
будет
иметь место и в некоторой окрестности
точки
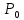
или
совпадать со знаком выражения (4.4).
При
этом получаем, что
1.
если
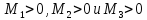
то
для
всех точек

принадлежащих проколотой окрестности
точки
и,
следовательно, точка

точка локального минимума.
2.
если
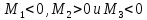
то
для
всех точек
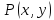
принадлежащих проколотой окрестности
точки
и,
следовательно, точка

точка локального максимума.
3.
в случаях
знак выражения
непостоянен и,
следовательно, точка
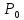
точка не является ни минимум, ни максимумом
.
4.
если
, точка
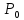
точка может быть или не быть точкой
минимума или максимума. В этом случае
требуются дополнительные исследования.
Объединяя
все выше сказанное, сформулируем теорему
ВЫУЧИТЬ!!!
Теорема
4.
(Достаточное условие экстремума ).
Пусть
функция
непрерывна вместе с частными производными
до второго порядка включительно в
окрестности стационарной точки
и главные миноры матрицы A
, составленной из частных производных
второго порядка, соответствующие
полному дифференциалу второго порядка
в этой точке определены, то
1.
если все главные миноры больше нуля,
точка

точка локального минимума.
2.
если все главные миноры чередуют знак,
начиная с отрицательного ,
точка
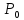
точка локального максимума.
3.
в других случаях , при условии, что
главные миноры отличны от нуля,
точка
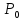
точка не является ни минимум, ни максимумом
.
4.
если
хоть один главный минор равен нулю,
точка
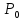
точка может быть или не быть точкой
минимума или максимума. В этом случае
требуются дополнительные исследования.
План
исследования на экстремум функций двух
переменных
1.
Используя
необходимые условия экстремума, находим
стационарные точки
:
Решением
системы являются стационарные точки
2.
Вычисляем
частные производные второго порядка в
каждой из найденных стационарных точек
. Выражение для дифференциала второго
порядка функции
имеет вид:
Составляем
матрицу
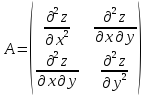
с
главными минорами
и
3.
Определяем,
является ли стационарная точка
точкой максимума или минимума функции
а)
если
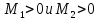
то
– точка
локального минимума.
б)
если
, то
– точка
локального максимума.
в)
в остальных случаях стационарная точка
– не является точкой экстремума,
если

г)
если

то
необходимы дополнительные исследования.
Пример
6.
Найти
и исследовать точки экстремума функции
1.
Используя
необходимые условия экстремума, находим
стационарные точки
:
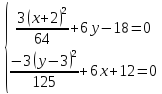
Система
имеет два решения:
Имеем
две стационарные точки
необходимо проверить являются они
точками
локального экстремума или нет.
2.
Вычисляем
частные производные второго порядка.
Выражение
для второго дифференциала функции
имеет
вид:
Составляем
матрицу
Матрица
A,
соответствующая второму дифференциалу,
зависит от точки
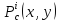
3.
Определяем,
являются ли стационарные точки
точками
максимума или минимума функции

Для этого подставляем координаты
стационарных точек
в выражение для

Для
первой стационарной точки
получим
с
главными минорами
и
вывод:
стационарная точка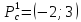
не является точкой экстремума.
Для
второй стационарной точки
получим
с
главными минорами
и
вывод:
стационарная точка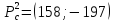
точка
локального минимума.
Ответ:
функция
имеет одну точку экстремума, точка
точка
локального минимума.
План
исследования на экстремум функций трех
переменных u=f(x,y,z).
1.
Используя
необходимые условия экстремума, находим
стационарные точки
:
Решением
системы являются стационарные точки
2.
Вычисляем
частные производные второго порядка в
каждой из найденных стационарных точек
. Выражение для дифференциала второго
порядка функции
имеет вид:
Составляем
матрицу
с
главными минорами
и
и
3.
Определяем
является ли стационарная точка
точкой максимума или минимума функции
u=f(x,y,z).
а)
если
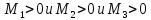
то
– точка
локального минимума.
б)
если
, то
– точка
локального максимума.
в)
в остальных случаях стационарная точка
– не является точкой экстремума,
если

г)
если
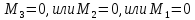
то
необходимы дополнительные исследования.
Пример
7.
Найти и исследовать точки экстремума
функции
1.
Используя
необходимые условия экстремума, находим
стационарные точки
:
Решением
системы является стационарная точка
2.
Вычисляем
частные производные второго порядка в
найденной стационарной точке
.
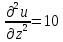
Выражение
для второго дифференциала функции
имеет вид:
или
Составляем
матрицу
главными
минорами, которой являются

и
3.
Определяем,
является ли стационарная точка
точкой локального экстремума ( точкой
максимума или минимума) функции
u=f(x,y,z).
Так
как
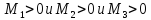
то
– точка
локального минимума.
Ответ:
точка
является
точкой минимума
функции
.
17