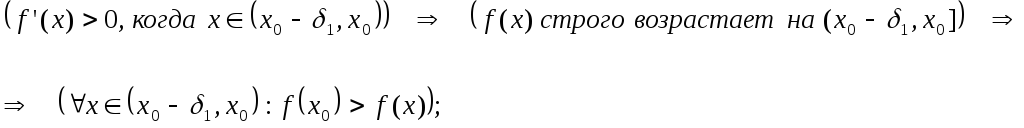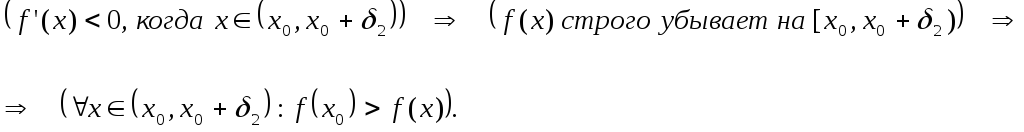Как найти стационарные точки функции одной переменной

1. Стационарные точки функции.
   Необходимое условие локального
   экстремума функции

2. Первое достаточное условие локального
   экстремума

3. Второе и третье достаточные условия
   локального экстремума

4. Наименьшее и наибольшее
   значения функции на сегменте

5. Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1.}
Пусть функция
определена на _{.
Точка
называется стационарной точкой функции
,
если
дифференцирована в точке
и .}

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция
определена на
_{и имеет в точке
локальный экстремум. Тогда выполняется
одно из условий:}

1. функция
   _{не имеет в точке
   производной;}

2. функция
   _{имеет в точке
   производную и .}

_{Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.}

_{Пример.
Пусть .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: .
Найдем теперь производную функции:}

_.

_{Точки, в которых производная
не существует: .
Стационарные точки функции:}

_.

_{Поскольку и ,
и
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция
определена на
_{и дифференцирована на этом интервале
везде за исключением, возможно, точки
,
но в этой точке
функция является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ,
в каждой из которых
сохраняет определенный знак, то}

_{1) функция
имеет локальный экстремум в точке ,
если
принимает значения разных знаков в
соответствующих полуокрестностях;}

<sub>2) функция
не имеет локальный экстремум в точке
,
если справа и слева от точки

имеет одинаковый знак.</sub>

_{Доказательство.
1) Предположим, что в полуокрестности
производная ,
а в
.}

_{Таким образом в точке
функция
имеет локальный экстремум, а именно –
локальный максимум, что и нужно было
доказать.}

_{2) Предположим, что слева
и справа от точки
производная сохраняет свой знак,
например, .
Тогда на
и
функция
строго монотонно возрастает, то есть:}

_,

_.

_{Таким образом экстремума
в точке
функция
не имеет, что и нужно было доказать.}

_{Замечание 1.
Если производная
при прохождении через точку
меняет знак с «+» на «-», то в точке
функция
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.}

_{Замечание 2.
Важным является условие непрерывности
функции
в точке .
Если это условие не выполняется, то
теорема 1 может не иметь места.}

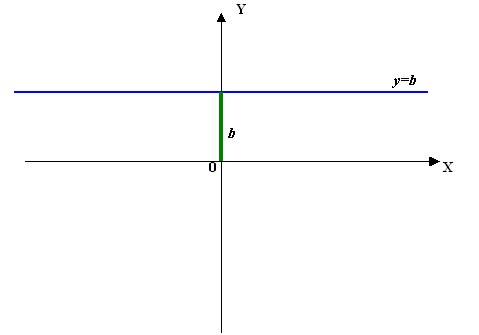
_{Пример.
Рассматривается функция (рис.1):}

Эта функция определена на
<sub>и непрерывна везде, кроме точки ,
где она имеет устранимый разрыв. При
прохождении через точку

меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение .
Теорема 1 не сработала потому, что в
точке
функция имела разрыв.</sub>

_{Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции
меняет свой знак в каждой левой и каждой
правой полуокрестности точки .}

_{Пример.
Рассматривается функция:}

_{Поскольку ,
то ,
а потому ,
но .
Таким образом:}

_,

_{т.е. в точке
функция
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.}

_{Для :}

_.

Для первого слагаемого правой
части полученной формулы имеем:

_,

_{а потому в малой окрестности
точки
знак производной определяется знаком
второго слагаемого, то есть:}

_,

<sub>а это означает, что в любой
окрестности точки

будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки :
.
Когда</sub>

_,

_то

_{(рис.2), а
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти стационарные точки функции

Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Вам понадобится

• – функция, которую необходимо исследовать на наличие стационарных точек;
• – определение стационарных точек: стационарные точки функции – это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.

Инструкция

Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.

Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений – в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.

Обратите внимание

При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.

Полезный совет

Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.

Внимание и концентрация на задаче также помогут с ней справиться – перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.

Источники:

• Производная функции – Википедия
• Критическая точка (математика) – Википедия

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Пример 1:

Исследовать функцию на экстремум и вычислить значение функции в точках экстремума:

Решение от преподавателя:

Решение.

Пример 2:

Исследуйте на экстремум функцию.

y = х² – 10х + 5

Решение от преподавателя:

Пример 3:

Найти экстремумы функций двух переменных

z = 2x³ + 6xy² – 30x – 24y.

Решение от преподавателя:

Пример 4:

Исследовать на экстремум:

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 

Достаточное условие экстремума функции одной переменной. 
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 6x²+6x 
или 
y’ = 6x(x+1) 
Приравниваем ее к нулю: 
6x²+6x = 0 
x₁ = 0 
x₂ = -1 
Вычисляем значения функции 
f(0) = -11 
f(-1) = -10 
Ответ: 
f_min = -11, f_max = -10 
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y” = 12x+6 
Вычисляем: 
y”(0) = 6>0 – значит точка x = 0 точка минимума функции. 
y”(-1) = -6<0 – значит точка x = -1 точка максимума функции. 

Пример 5:

Найти стационарные точки и исследовать на экстремум функцию

z = x² + y² – 2x – 2y+ 8

Решение от преподавателя:

Исследовать на экстремум функцию z = x² + y² – 2x – 2y+ 8

1. Найдем частные производные. 


2. Решим систему уравнений. 
2x-2 = 0 
2y-2 = 0 
Получим: x = 1, y = 1 
критическая  точка   M₁(1;1) 
3. Найдем частные производные второго порядка. 



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀). 
Вычисляем значения для точки M₁(1;1) 



AC – B² = 4 > 0 и A > 0 , то в точке M₁(1;1) имеется минимум z(1;1) = 6 
Вывод: В точке M₁(1;1) имеется минимум z(1;1) = 6;

Пример 6:

Исследовать на экстремум функцию:

Решение от преподавателя:

Пример 7:

Исследовать функцию z(x,y) на экстремум

Решение от преподавателя:

Пример 8:

Исследовать на экстремум функцию:

Решение от преподавателя:

Вычислим производную этой функции и найдем стационарные точки, в которых она обращается в нуль:

Решая это уравнение, находим корни x₁ = 1 и x₂ = 2. Они являются подозрительными на экстремум в данной задаче. При этом знаки производной нашей функции распределены следующим образом:

Согласно теореме о достаточном условии экстремума первого порядка, полученные точки являются точками локального экстремума, а именно: x₁ = 1 — точка локального максимума, причем f(x₁) = 11, а x₂ = 2 — точка локального минимума, причем f(x₂) = 10.

Глобальных экстремумов в этой задаче нет. Это видно из того, что

Итак, локальный максимум достигается в точке x = 1 и равен 11, локальный минимум достигается в точке x = 2, и равен 10.

Пример 9:

Исследуйте на экстремум функцию z = z(x;y).

Решение от преподавателя:

Пример 10:

Исследовать на экстремум:

y = (2*x-8)*(9*x+1) 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 36x-70 
Приравниваем ее к нулю: 
36x-70 = 0 

Вычисляем значения функции 

Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y” = 36 
Вычисляем: 

значит эта точка – минимума функции.

Пример 11:

Найти экстремумы функции z(x,y) при данном условии:

Решение от преподавателя:

Пример 12:

Исследовать на экстремум функцию:

Решение от преподавателя:

Найдем производную f′ (x) = e^x − e^−x . Чтобы найти критические точки функции f(x), приравняем эту производную к нулю:

Очевидно, что точка x = 0 является решением последнего уравнения. Функция f′(x) строго возрастает (поскольку ). Поэтому она отрицательна при x < 0 и положительна при x > 0.

Следовательно, точка x = 0 является точкой строгого локального минимума функции f(x), и f(0) = 2 — соответствующее минимальное значение.

В данной ситуации можно также применить теорему о достаточном условии экстремума второго порядка. Поскольку f′′(0) = 2 > 0, функция f(x) имеет строгий локальный минимум в точке x = 0.

Кроме того, этот минимум глобальный, потому что

Ответ: точка x = 0 является точкой глобального минимума для исследуемой функции и f_min = f(0) = 2.

Пример 13:

Найти наибольшее и наименьшее значения функции z(x,y) в области D:

Решение от преподавателя:

Пример 14:

Исследовать на экстремум функцию:

y = x³+6*x²-4, [-4;1]. 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 3x²+12x 
или 
y’ = 3x(x+4) 
Приравниваем ее к нулю: 
3x(x+4) = 0 
x₁ = 0 
x₂ = -4 
Вычисляем значения функции на концах отрезка 
f(0) = -4 
f(-4) = 28 
f(-4) = 28.0000000000000 
f(1) = 3.00000000000000 

Ответ: f_min = -4, f_max = 28.

Пример 15:

Исследовать на экстремум функцию

Решение от преподавателя:

Как обычно, начнем с нахождения производной исследуемой функции и точек, подозрительных на экстремум:

Легко видеть, что точка x = 0 является критической.

Найдем вторую производную:

Очевидно, f′′(0) = 0. Воспользуемся теоремой о достаточном условии экстремума n-го порядка и будем дифференцировать функцию до того момента, пока не появится отличная от нуля производная:

Значит, x = 0 — точка локального минимума функции f(x).

Из предыдущего примера следует, что при . В то же время . Поэтому f′′(x) > 0 при . Отсюда следует, что производная f′(x) обращается в нуль в единственной точке x = 0.

Так как ,  минимум в точке x = 0 является глобальным.

Ответ: есть один глобальный минимум f(0) = 4.

Пример 16:

С помощью второй производной исследуйте на экстремум функцию . Найдите наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2].

Решение от преподавателя:

Определяем критические точки

Определяем вторую производную функции

Определяем знаки второй производной в критических точках

Т. к. вторая производная положительная, то в точке х=0 минимум

Т. к. вторая производная отрицательная, то в точке х=1 максимум

Наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2]

Т. к. обе критические точки принадлежат указанному отрезку, то определяем значения функции в полученных точках и на концах отрезка

Т. о., М=у(-1)=6 m=у(2)=-3

Пример 17:

Исследовать на экстремум функцию:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственная подозрительная на экстремум точка (в которой все частные производные обращаются в нуль) — это точка a = (3, −2, −1).

Определим, есть ли в этой точке экстремум. Для этого найдем все частные производные второго порядка

и составим из них матрицу полной второй производной f′′(a):

Главные миноры этой матрицы чередуют знаки:

По теореме (достаточное условие экстремума второго порядка) в точке a локальный максимум. Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

Пример 18:

Найти экстремумы функции:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственной стационарной точкой будет точка a = (0, 0).

Посмотрим, есть ли в ней экстремум. Для этого вычислим частные производные второго порядка

и составим из них матрицу второй производной в точке a:

Очевидно, ее определитель равен нулю. Значит, достаточные условия экстремума из теоремы (достаточное условие экстремума второго порядка) в данном случае не применимы.

Придется использовать определение экстремума. Рассмотрим разность . Она больше нуля при всех y > 0 и меньше нуля при y < 0. Поэтому в точке a = (0, 0) нет экстремума.

Ответ: у функции f нет экстремумов.

Пример 19:

Найти экстремумы функции

Решение от преподавателя:

Очевидно,

и единственная стационарная точка — это a = (0, 0).

Далее вычисляем частные производные второго порядка

и выписываем матрицу второй производной в точке a:

Ее определитель равен нулю. Достаточные условия экстремума опять не работают. С другой стороны, . Поэтому в точке (0, 0) глобальный минимум.

Ответ: есть один глобальный минимум f(0, 0) = 0.

Пример 20:

Исследовать на экстремумы функцию.

Решение от преподавателя:

Содержание:

• Необходимое условие экстремума
• Первое достаточное условие экстремума
• Второе достаточное условие экстремума

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума –
локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка $x_{0}$ называется точкой строгого локального
максимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет справедливо
строгое неравенство $f(x) lt fleft(x_{0}right)$.

Точка $x_{0}$ называется точкой строгого локального
минимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет
справедливо строгое неравенство $f(x)>fleft(x_{0}right)$.

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Необходимое условие экстремума

Точки, в которых производная равна нулю: $f^{prime}(x)=0$,
называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются
критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения
уравнения $f^{prime}(x)=0$), либо это точки, в которых производная
$f^{prime}(x)$ не существует.

Первое достаточное условие экстремума

Если производная $f^{prime}(x)$ при переходе через точку
$x_{0}$ не меняет знак, то экстремума в точке
$x=x_{0}$ нет.

Таким образом, для того чтобы исследовать функцию $y=f(x)$
на экстремум, необходимо:

Второе достаточное условие экстремума

Читать дальше: наибольшее и наименьшее значение функции.