Онлайн калькулятор для определения стационарных точек.
Стационарные точки – это точки, в которых производная функции равна 0 или не существует.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Как найти стационарные точки функции
Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Вам понадобится
- – функция, которую необходимо исследовать на наличие стационарных точек;
- – определение стационарных точек: стационарные точки функции – это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.
Инструкция
Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.
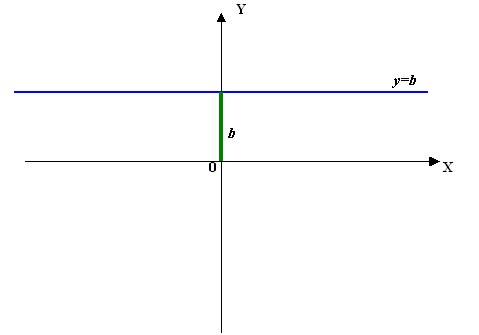
Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений – в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.
Обратите внимание
При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.
Полезный совет
Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.
Внимание и концентрация на задаче также помогут с ней справиться – перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.
Источники:
- Производная функции – Википедия
- Критическая точка (математика) – Википедия
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как находить стационарные точки?
Мастер
(1676),
закрыт
13 лет назад
Светлана***
Мастер
(1081)
13 лет назад
СТАЦИОНАРНАЯ ТОЧКА [stationary point] — точка, в которой все частные производные первого порядка рассматриваемой функции от нескольких переменных равны нулю и тем самым градиент дифференцируемой функции обращается в нуль. Следовательно надо найти производную, приравнять к нулю и решить получившееся уравнение. Корни и будут стационарными точками. Если перед вами дробь, то надо найти производную и приравнять числитель к нулю. Так Вы найдете стационарные точки. Приравняв к нулю знаменатель, Вы найдете критические точки. Вот и все. Удачи 🙂
Bota SharipzhanМастер (1676)
13 лет назад
Но ведь так же находят и точки экстремумов! Какая разница между нахождением стационарных точек и точек экстремумов?
-
Стационарные точки функции.
Необходимое условие локального
экстремума функции -
Первое достаточное условие локального
экстремума -
Второе и третье достаточные условия
локального экстремума -
Наименьшее и наибольшее
значения функции на сегменте -
Выпуклые функции и точки перегиба
1. Стационарные точки функции. Необходимое условие локального экстремума функции
Определение 1.
Пусть функция ![]()
определена на ![]() .
.
Точка ![]()
называется стационарной точкой функции
![]() ,
,
если ![]()
дифференцирована в точке ![]()
и ![]() .
.
Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция ![]()
определена на ![]()
и имеет в точке ![]()
локальный экстремум. Тогда выполняется
одно из условий:
-
функция

не имеет в точке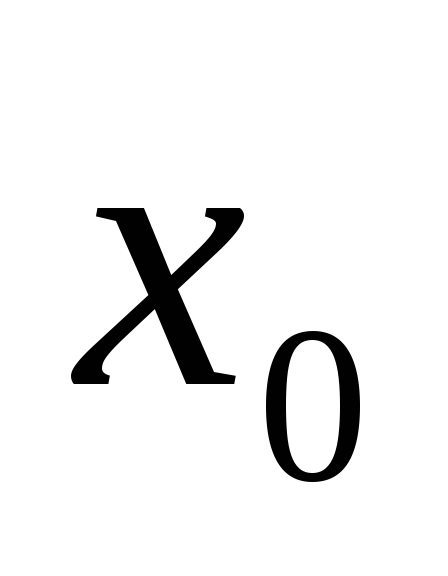
производной; -
функция
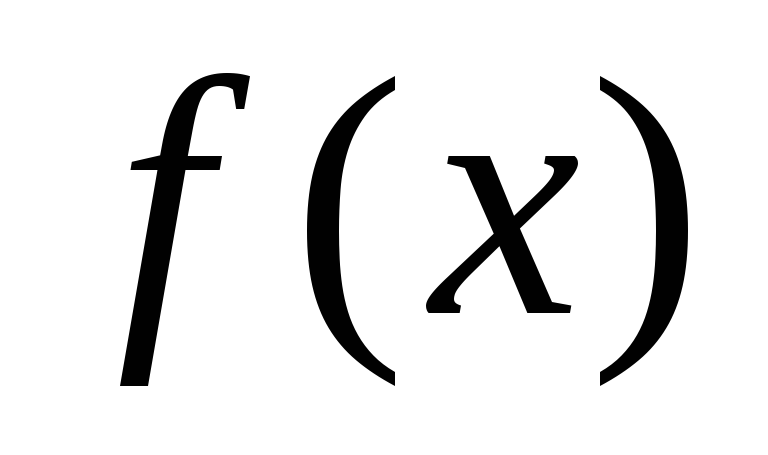
имеет в точке
производную и .
.
Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.
Пример.
Пусть ![]() .
.
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: ![]() .
.
Найдем теперь производную функции:
![]() .
.
Точки, в которых производная
не существует: ![]() .
.
Стационарные точки функции:
![]() .
.
Поскольку и ![]() ,
,
и ![]()
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.
2. Первое достаточное условие локального экстремума
Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция ![]()
определена на ![]()
и дифференцирована на этом интервале
везде за исключением, возможно, точки
![]() ,
,
но в этой точке ![]()
функция ![]() является
является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ![]() ,
,
в каждой из которых ![]()
сохраняет определенный знак, то
1) функция ![]()
имеет локальный экстремум в точке ![]() ,
,
если ![]()
принимает значения разных знаков в
соответствующих полуокрестностях;
2) функция ![]()
не имеет локальный экстремум в точке
![]() ,
,
если справа и слева от точки ![]()
![]()
имеет одинаковый знак.
Доказательство.
1) Предположим, что в полуокрестности ![]()
производная ![]() ,
,
а в ![]()
![]() .
.
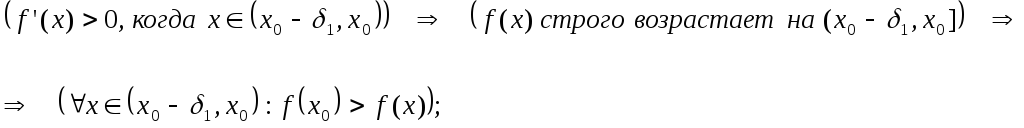
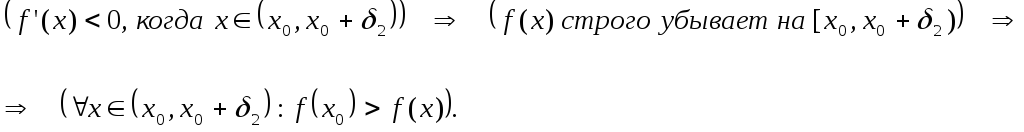
Таким образом в точке ![]()
функция ![]()
имеет локальный экстремум, а именно –
локальный максимум, что и нужно было
доказать.
2) Предположим, что слева
и справа от точки ![]()
производная сохраняет свой знак,
например, ![]() .
.
Тогда на ![]()
и ![]()
функция ![]()
строго монотонно возрастает, то есть:
![]() ,
,
![]() .
.
Таким образом экстремума
в точке ![]()
функция ![]()
не имеет, что и нужно было доказать.
Замечание 1.
Если производная ![]()
при прохождении через точку ![]()
меняет знак с «+» на «-», то в точке ![]()
функция ![]()
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.
Замечание 2.
Важным является условие непрерывности
функции ![]()
в точке ![]() .
.
Если это условие не выполняется, то
теорема 1 может не иметь места.
Пример.
Рассматривается функция (рис.1):


Эта функция определена на ![]()
и непрерывна везде, кроме точки ![]() ,
,
где она имеет устранимый разрыв. При
прохождении через точку ![]()
![]()
меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки ![]()
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение ![]() .
.
Теорема 1 не сработала потому, что в
точке ![]()
функция имела разрыв.
Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции ![]()
меняет свой знак в каждой левой и каждой
правой полуокрестности точки ![]() .
.
Пример.
Рассматривается функция:

Поскольку ![]() ,
,
то ![]() ,
,
а потому ![]() ,
,
но ![]() .
.
Таким образом:
![]() ,
,
т.е. в точке ![]()
функция ![]()
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.
Для ![]() :
:
![]() .
.
Для первого слагаемого правой
части полученной формулы имеем:
![]() ,
,
а потому в малой окрестности
точки ![]()
знак производной определяется знаком
второго слагаемого, то есть:
![]() ,
,
а это означает, что в любой
окрестности точки ![]()
![]()
будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки ![]() :
:
![]() .
.
Когда
![]() ,
,
то
![]()
(рис.2), а ![]()
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прежде всего, напишем уравнение математической функции
y = f(x) (1)
где х – аргумент функции, а у – сама функция. То есть мы задаем какое-либо значение аргумента х и вычисляем по уравнению (1) значение функции в этой точке. Принято рисовать график функции y = f(x). Рисуем оси координат х и у. Значение х откладываем по горизонтальной оси х. Эта ось называется осью абсцисс. По вертикали откладываем значение вычисленной функции у (эта ось называется осью ординат). На рисунке приведен график некоторой функции

Как мы видим при х = 3 и х = 8 функция у имеет максимумы. А при х = 5 функция имеет минимум. То есть функция y = f(x) может иметь как минимумы, так и максимумы. Итак
Точка максимума – значение х, при котором функция имеет максимум.
Точка минимума – значение х, при котором функция имеет минимум.
Обе эти точки называются общим словом – экстремум. То есть в точках экстремума функция имеет максимальное или минимальное значение.
Нам еще потребуется знание, что такое производная функции. Если мы знаем саму функцию (1), то производная берется следующим образом
dy/dx = df(x)/dx (2)
Смысл производной – тангенс угла наклона функции в данной точке х. Можно провести в любой точке функции касательную линию и угол между этой касательной и осью х и будет определять угол наклона. Но удобнее вычислять не сам угол наклона α, а тангенс этого угла tgα. Иными словами,
tgα = dy/dx = df(x)/dx (3)
Как видно из вышеприведенного рисунка в точках экстремума функции tgα = 0. То есть производная в этих точках равна нулю. Если нам известно уравнение функции (1), то приравнивая производную к нулю, получаем алгебраическое уравнение для вычисления точек максимума и минимума
df(x)/dx (3) = 0 (4)
А что такое критические и стационарные точки функции? Точки экстремума функции (то есть там, где функция имеет максимум или минимум) иногда называю еще и стационарными точками. Это на приведенном выше рисунке точки х = 3, 5 и 8. Иногда бывает, что функция у(х) имеет концы, то есть кривая функции не уходит на бесконечность ни влево ни вправо. Например, на вышеприведенном рисунке будем считать, что эта функция расположена между точками х = -1 и х = 10. Если бы в этих крайних точках функция имела бы минимум (или максимум), то есть экстремум (производная равна нулю), то эти точки не называются стационарными.
А вот внутренние точки функции, в которых функция непрерывна, но в этих точках производная не существует, называются критическими точками. Смотри рисунок ниже

В точке х = 0 эта функция имеет максимум, но в этой точке имеется и перелом функции. Острый максимум. Производная (наклон функции) слева от точки х = 0 положительная, а справа от этой точки производная отрицательная. Это критическая точка. А вот в точке х = 1 имеется минимум (производная равна нулю), но функция меняет знак без перелома (то есть постепенно). Это точка минимума и точка стационарная.
