Стандартизированный коэффициент
регрессии рассчитывается по формуле
βj – коэффициент
при факторе хj.
Определяет силу влияние вариации хj
на вариацию результативного признака
у при отвлечении от сопутствующего
влияния вариаций других факторов,
входящих в уравнение регрессии.
Т.к. βj сравнимы
между собой, то по величине данных
коэффициентов можно ранжировать факторы
по силе их воздействия на результат.

Наибольшее влияние на вариацию у, т.е.
отношение прибыли ко всем активам,
оказывает фактор х1 , доля ГКО в
активах, т.к. β1 наибольшие. Далее
по силе влияние – х1 и наименьшее
влияние оказывает фактор х2.
Уравнение регрессии в стандартизированном
масштабе.
Общий вид:

стандартизированные параметры регрессии
Смысл стандартизированных коэффициентов
βj позволяет
использовать их при отсеве факторов,
т.е. из модели исключаются факторы с
наименьшим значением βj.
Вывод: При отклонении х1 на 1 ,
при неизменном х2 и х3 у
увеличивается в среднем на 0, 6957 (βj)
Коэффициенты условно чистой регрессии
можно выразить в виде относительно
сравнимых показателей связи – средних
коэффициентов эластичности.

Средний коэффициент эластичности
показывает, что при изменении фактора
хj на 1% результативный
признак изменяется на Эj
% его средней величины при неизмененном
влиянии всех остальных факторов.
Для множественной регрессии включающей
2 факторных признака коэффициенты
стандартизированной регрессии могут
быть найдены по следующим факторам:


5. Система показателей тесноты многофакторной связи
Многофакторная система требует не
одного, а нескольких показателей тесноты
связи, имеющих разный смысл и применение.
Основой измерения связей является
матрица парных коэффициентов. По ней
можно судить и тесноте связей факторов
с результативным признаком и между
собой.
На основе матрицы вычисляется наиболее
показатель тесноты связей всех водящих
в уравнение регрессии факторов с
результативным признаком, т.е. коэффициент
множественной детерминации, который
определяется как частное от
деления определителя матрицы Δ* на
общийΔ.
Существует 2 способа вычисления R2
:
-
через
корреляционное отношение
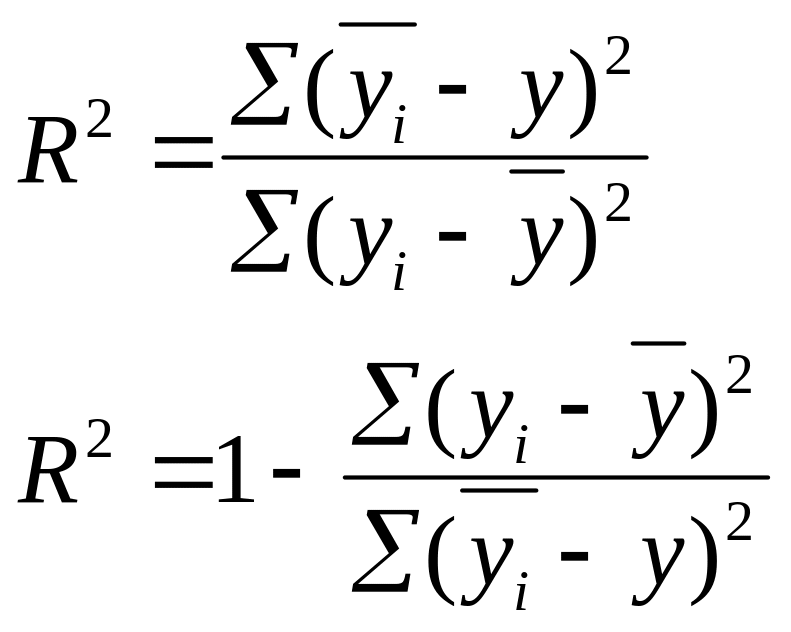
т.о. 56,7 % вариации у определяется вариацией
трех факторов, включенных в модель.
Показывает, что связь между х1,
х2, х3 и у достаточно сильная.
Данный способ рационален в то случае,
если n мало.
-
через
определители матрицы.

Подставляя значения из матрицы парных
коэффициентов корреляции произведем
расчеты


Произведем расчеты

Это более точный расчет.
Для уравнения в стандартизированном
масштабе:

Множественный коэффициент детерминации
характеризует отношение части вариации
результативного признака, объясненного
за счет вариации, входящей в уравнение
факторов к общей вариации результативного
признака за счет всех факторов.
Все три фактора объясняют 57,2% вариации
результативного признака.
При решении проблемы отбора факторов,
т.е. целесообразности включения в модель
того или иного фактора используется
частичные коэффициенты корреляции. Они
характеризуют тесноту связи между
результативным фактором и соответствующим
факторным признаком, при устранении
влияния других факторов включенных в
уравнение регрессии.
Показатели частичной корреляции
представляют собой отношение сокращения
остаточной дисперсии, за счет
дополнительного включения в анализ
нового фактора к остаточной дисперсии,
имевшей место до введения его в модель.
Разложение коэффициента множественной
дисперсии.
Это необходимо для того, чтобы:
-
измерить
роль каждого фактора -
измерить
«системный эффект», т.е. степень
системности факторов в изученном
объекте.
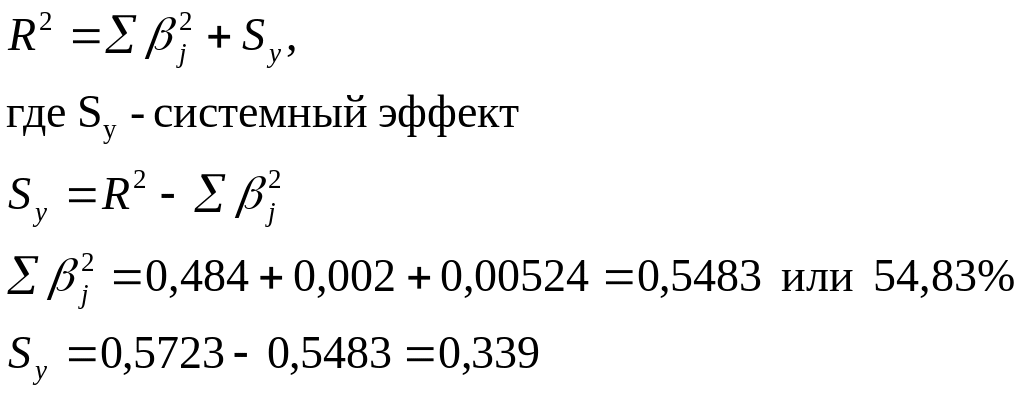
Следовательно, роль системного эффекта
невелика.
Выводы:
-
главную
роль вариации у играет вариация х. -
добавление
факторов х2, х3 мало увеличило
R2 (х2, влияет
на 0,2%, а вариация х3 объясняет
лишь 5,24% вариации у). -
системный
эффект слабый, т.е. факторы слабо связаны,
либо их значение не согласуется.
Если системный эффект мал, или это
отрицательное число, то значит наблюдается
несистемность, что является отрицательным
явлением.
Для измерения тесноты связи результативного
фактора с каждым из фактических признаков
используются следующие показатели.
Коэффициент раздельной детерминации
произведение коэффициента корреляции
на его β коэффициент.
Сумма коэффициентов раздельной
детерминации равна множественному
коэффициенту детерминации

Т.о. за счет х1 объясняется 49,95%
вариации у, за счет вариации х2 –
1,79% вариации у и за счет вариации х3
– 5,52%.
Сумма коэффициентов раздельной
детерминации равна некорректированному
коэффициенту множественной регрессии
R2.
Недостатки коэффициента раздельной
детерминации:
-
коэффициенты
раздельной детерминации включают в
себя коэффициенты парной корреляции,
измеряющие не чистое влияние фактора,
абстрагирующиеся от влияния других
факторов, входящих в уравнение регрессии. -
сама идея
о том, что совокупность влияния каждого
фактора (их суммы) равна совокупности
влияния всех факторов противоречит
системному подходу в исследованиях.
Система факторов – не простая их сумма,
т.к. система предполагает внутренние
связи и взаимодействия составных ее
элементов. Действие системы не равно
сумме взаимодействий составных ее
элементов, к нему добавляется еще и
«системный эффект».
Методом, отвечающим системному подходу
является метод разложения коэффициента
множественной детерминации на сумму
чистых влияний каждого фактора,
выраженного β2 , и показателя
системного эффекта Sy
.
Коэффициент частичной детерминации.
Коэффициент частичной детерминации хm
– доля вариации у, дополнительно
объясняется при включении фактора хm
, после остальных факторов в уравнении
регрессии, в величине вариации у, не
объясняясь включенными факторами.

Данный показатель используется при
решении вопроса о целесообразности
включения в модель исследованного
фактора.
Конфликты парной корреляции и детерминации
не сравнимы между собой, т.к. представляют
данные от разных величин. Их сумма часто
больше единицы и неограниченна.

Отсюда имеем частичные коэффициенты
детерминации

Включение фактора х1 объясняет
46,8 % вариации у. Включение фактора х2,
объясняет 0,2 % ранее необъяснимой вариации
у, а х3 – 10,5 % ранее необъяснимой
вариации у.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Эконометрические модели
Условие задачи
По 20
предприятиям региона изучается зависимость выработки продукции на одного
работника
(тыс.руб.) от ввода в действие новых основных
фондов
(% от стоимости фондов на
конец года) и от удельного
веса рабочих высокой квалификации в общей численности рабочих
(смотри таблицу своего варианта).
Требуется:
| № |
|
|
|
№ |
|
|
|
| 1 | 7 | 3.7 | 9 | 11 | 10 | 6.8 | 21 |
| 2 | 7 | 3.7 | 11 | 12 | 11 | 7.4 | 23 |
| 3 | 7 | 3.9 | 11 | 13 | 11 | 7.8 | 24 |
| 4 | 7 | 4.1 | 15 | 14 | 12 | 7.5 | 26 |
| 5 | 8 | 4.2 | 17 | 15 | 12 | 7.9 | 28 |
| 6 | 8 | 4.9 | 19 | 16 | 12 | 8.1 | 30 |
| 7 | 8 | 5.3 | 19 | 17 | 13 | 8.4 | 31 |
| 8 | 9 | 5.1 | 20 | 18 | 13 | 8.7 | 32 |
| 9 | 10 | 5.6 | 20 | 19 | 13 | 9.5 | 33 |
| 10 | 10 | 6.1 | 21 | 20 | 14 | 9.7 | 35 |
Решение задачи
Для
удобства проведения расчетов поместим результаты промежуточных расчетов в
таблицу:
| № |
|
|
|
|
|
|
|
|
|
| 1 | 7 | 3.7 | 9 | 25.9 | 63 | 33.3 | 13.69 | 81 | 49 |
| 2 | 7 | 3.7 | 11 | 25.9 | 77 | 40.7 | 13.69 | 121 | 49 |
| 3 | 7 | 3.9 | 11 | 27.3 | 77 | 42.9 | 15.21 | 121 | 49 |
| 4 | 7 | 4.1 | 15 | 28.7 | 105 | 61.5 | 16.81 | 225 | 49 |
| 5 | 8 | 4.2 | 17 | 33.6 | 136 | 71.4 | 17.64 | 289 | 64 |
| 6 | 8 | 4.9 | 19 | 39.2 | 152 | 93.1 | 24.01 | 361 | 64 |
| 7 | 8 | 5.3 | 19 | 42.4 | 152 | 100.7 | 28.09 | 361 | 64 |
| 8 | 9 | 5.1 | 20 | 45.9 | 180 | 102 | 26.01 | 400 | 81 |
| 9 | 10 | 5.6 | 20 | 56 | 200 | 112 | 31.36 | 400 | 100 |
| 10 | 10 | 6.1 | 21 | 61 | 210 | 128.1 | 37.21 | 441 | 100 |
| 11 | 10 | 6.8 | 21 | 68 | 210 | 142.8 | 46.24 | 441 | 100 |
| 12 | 11 | 7.4 | 23 | 81.4 | 253 | 170.2 | 54.76 | 529 | 121 |
| 13 | 11 | 7.8 | 24 | 85.8 | 264 | 187.2 | 60.84 | 576 | 121 |
| 14 | 12 | 7.5 | 26 | 90 | 312 | 195 | 56.25 | 676 | 144 |
| 15 | 12 | 7.9 | 28 | 94.8 | 336 | 221.2 | 62.41 | 784 | 144 |
| 16 | 12 | 8.1 | 30 | 97.2 | 360 | 243 | 65.61 | 900 | 144 |
| 17 | 13 | 8.4 | 31 | 109.2 | 403 | 260.4 | 70.56 | 961 | 169 |
| 18 | 13 | 8.7 | 32 | 113.1 | 416 | 278.4 | 75.69 | 1024 | 169 |
| 19 | 13 | 9.5 | 33 | 123.5 | 429 | 313.5 | 90.25 | 1089 | 169 |
| 20 | 14 | 9.7 | 35 | 135.8 | 490 | 339.5 | 94.09 | 1225 | 196 |
| Сумма | 202 | 128.4 | 445 | 1384.7 | 4825 | 3136.9 | 900.42 | 11005 | 2146 |
| Ср.знач. | 10.100 | 6.420 | 22.250 | 69.235 | 241.250 | 156.845 | 45.021 | 550.250 | 107.300 |
Найдем
средние квадратические отклонения признаков:
Линейное уравнение множественной регрессии
Для
нахождения параметров линейного уравнения множественной регрессии:
необходимо
решить следующую систему линейных уравнений относительно неизвестных параметров
:
либо
воспользоваться готовыми формулами:
Рассчитаем
сначала парные коэффициенты корреляции:
Таким
образом, получили следующее уравнение множественной регрессии:
Стандартизированное уравнение множественной регрессии
Коэффициенты
и
стандартизированного уравнения регрессии
находятся по формулам:
То есть
уравнение будет выглядеть следующим образом:
Так как
стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно
сказать, что ввод в действие новых основных фондов оказывает большее влияние на
выработку продукции, чем удельный вес рабочих высокой квалификации.
Коэффициенты эластичности
Сравнивать
влияние факторов на результат можно также при помощи средних коэффициентов
эластичности:
Вычисляем:
Т.е.
увеличение только основных фондов (от своего среднего значения) или только
удельного веса рабочих высокой квалификации на 1% увеличивает в среднем
выработку продукции на 0,503% или 0,214% соответственно. Таким образом,
подтверждается большее влияние на результат
фактора
, чем фактора
.
Коэффициенты парной корреляции
Коэффициенты парной корреляции мы уже нашли:
Они
указывают на весьма сильную связь каждого фактора с результатом, а также
высокую межфакторную зависимость (факторы
и
явно коллинеарны, так как
). При такой сильной
межфакторной зависимости рекомендуется один из факторов исключить из
рассмотрения.
Частные коэффициенты корреляции
Частные
коэффициенты корреляции характеризуют тесноту связи между результатом и
соответствующим факторов при элиминировании (устранении влияния) других
факторов, включенных в уравнение регрессии.
При двух
факторах частные коэффициенты корреляции рассчитываются следующим образом:
Если
сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за
высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные
оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у
которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Коэффициент множественной корреляции
Коэффициент
множественной корреляции определить по формуле:
Коэффициент
множественной корреляции показывает на весьма сильную связь всего набора
факторов с результатом.
Нескорректированный коэффициент множественной детерминации
оценивает долю вариации результата за счет
представленных в уравнении факторов в общей вариации результата. Здесь эта доля
составляет 98.4% и указывает на высокую степень обусловленности вариации
результата вариацией факторов, иными словами – на весьма тесную связь факторов
с результатом.
Скорректированный
коэффициент множественной корреляции:
определяет
тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает
такую оценку тесноты связи, которая не зависит от числа факторов и поэтому
может сравниваться по разным моделям с разным числом факторов. Оба коэффициента
указывают на высокую (более 95%) детерминированность результата
в модели факторами
и
.
Критерий Фишера
Оценку
надежности уравнения регрессии в целом и показателя тесноты связи
дает
–критерий Фишера:
В нашем
случае фактическое значение
–критерия Фишера:
Получили,
что
(при
), то есть вероятность
случайно получить такое значение
– критерия не превышает допустимый уровень
значимости 5%. Следовательно, полученное значение не случайно, оно
сформировалось под влиянием существенных факторов, то есть подтверждается
статистическая значимость всего уравнения и показателя тесноты связи
.
С
помощью частных
–критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
при помощи формул:
Найдем
и
.
Получили,
что
. Следовательно, включение
в модель фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
Если
поменять первоначальный порядок включения факторов в модель и рассмотреть
вариант включения
после
, то результат расчета
частного
–критерия для
будет иным.
, то есть вероятность его
случайного формирования меньше принятого стандарта
. Следовательно, значение
частного
– критерия для дополнительно включенного
фактора
не случайно, является статистически значимым,
надежным, достоверным: прирост факторной дисперсии за счет дополнительного
фактора
является существенным.
Фактор
должен присутствовать в уравнении, в том числе в варианте, когда он
дополнительно включается после фактора
.
Стандартизированные и нестандартизированные коэффициенты регрессии
17 авг. 2022 г.
читать 3 мин
Множественная линейная регрессия — полезный способ количественной оценки взаимосвязи между двумя или более переменными-предикторами и переменной- откликом .
Обычно, когда мы выполняем множественную линейную регрессию, результирующие коэффициенты регрессии нестандартизированы , то есть они используют необработанные данные для поиска линии наилучшего соответствия.
Однако, когда переменные-предикторы измеряются в совершенно разных масштабах, может быть полезно выполнить множественную линейную регрессию с использованием стандартизированных данных, что приводит к стандартизированным коэффициентам.
Чтобы помочь вам понять эту идею, давайте рассмотрим простой пример.
Пример: стандартизированные и нестандартизированные коэффициенты регрессии
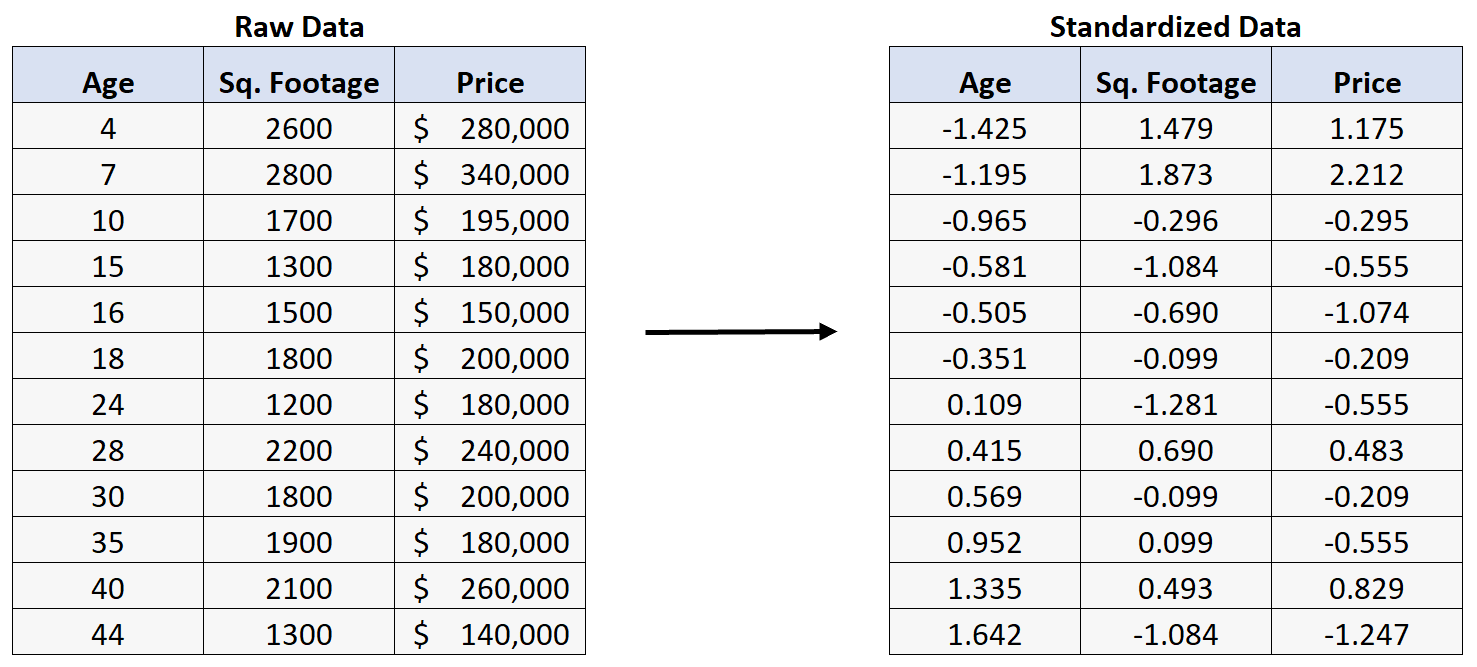
Предположим, у нас есть следующий набор данных, который содержит информацию о возрасте, площади и цене продажи 12 домов:
Предположим, что затем мы выполняем множественную линейную регрессию, используя возраст и площадь в квадратных футах в качестве переменных-предикторов и цену в качестве переменной-отклика.Вот результат регрессии :
Коэффициенты регрессии в этой таблице нестандартизированы , то есть они использовали необработанные данные для соответствия этой модели регрессии. На первый взгляд кажется, что возраст оказывает гораздо большее влияние на цену дома, так как его коэффициент в таблице регрессии составляет -409,833 по сравнению со всего лишь 100,866 для предикторной переменной площади в квадратных футах .
Однако стандартная ошибка намного больше для возраста по сравнению с площадью в квадратных футах, поэтому соответствующее значение p на самом деле велико для возраста (p = 0,520) и мало для площади в квадратных футах (p = 0,000).
Причина крайних различий в коэффициентах регрессии заключается в крайних различиях в шкалах для двух переменных:
- Значения возраста варьируются от 4 до 44 лет.
- Значения квадратных метров варьируются от 1200 до 2800.
Предположим, что вместо этого мы стандартизируем исходные необработанные данные, преобразуя каждое значение исходных данных в z-оценку:
Если мы затем выполним множественную линейную регрессию, используя стандартизированные данные, мы получим следующий результат регрессии:
Коэффициенты регрессии в этой таблице стандартизированы , то есть они использовали стандартизированные данные для соответствия этой модели регрессии. Способ интерпретации коэффициентов в таблице следующий:
- Увеличение возраста на одно стандартное отклонение связано со снижением стоимости дома на 0,92 стандартного отклонения, при условии, что площадь в квадратных футах остается неизменной.
- Увеличение площади в квадратных футах на одно стандартное отклонение связано с увеличением стоимости дома на 0,885 стандартного отклонения, если предположить, что возраст остается постоянным.
Сразу видно, что квадратные метры оказывают гораздо большее влияние на цену дома, чем возраст. Также обратите внимание, что p-значения для каждой переменной-предиктора точно такие же, как и в предыдущей модели регрессии.
Связанный: Как рассчитать Z-баллы в Excel
Когда использовать стандартизированные и нестандартизированные коэффициенты регрессии
В зависимости от ситуации могут быть полезны как стандартизированные, так и нестандартизированные коэффициенты регрессии. Особенно:
Нестандартизированные коэффициенты регрессии полезны, когда вы хотите интерпретировать эффект, который изменение на одну единицу переменной предиктора оказывает на переменную отклика. В приведенном выше примере мы могли бы использовать нестандартизированные коэффициенты регрессии из первой регрессии, чтобы понять точную связь между переменными-предикторами и переменной ответа:
- Увеличение возраста на одну единицу было связано со снижением цены дома в среднем на 409 долларов , если предположить, что площадь в квадратных футах остается неизменной. Этот коэффициент оказался статистически недостоверным (р=0,520).
- Увеличение площади на одну единицу было связано с увеличением цены дома в среднем на 100 долларов , если предположить, что возраст оставался постоянным. Этот коэффициент также оказался статистически значимым (р=0,000).
Стандартизированные коэффициенты регрессии полезны, когда вы хотите сравнить влияние различных переменных-предикторов на переменную отклика. Поскольку каждая переменная стандартизирована, вы можете увидеть, какая переменная оказывает наибольшее влияние на переменную ответа.
Одним из недостатков стандартизированных коэффициентов регрессии является то, что их немного сложнее интерпретировать. Например, легче понять влияние увеличения возраста на одну единицу на цену дома по сравнению с влиянием увеличения на одну единицу стандартного отклонения на цену дома.
Дополнительные ресурсы
Как читать и интерпретировать таблицу регрессии
Как интерпретировать коэффициенты регрессии
Как выполнить множественную линейную регрессию в Excel
Задача
По 20
предприятиям региона изучается зависимость выработки продукции на одного
работника
(тыс.руб.) от ввода в действие новых основных
фондов
(% от стоимости фондов на
конец года) и от удельного веса рабочих высокой квалификации в общей
численности рабочих
(смотри таблицу своего варианта).
Требуется:
Построить линейную модель множественной регрессии. Записать стандартизированное
уравнение множественной регрессии. На основе стандартизированных коэффициентов
регрессии и средних коэффициентов эластичности ранжировать факторы по степени
их влияния на результат.
Найти
коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Найти
скорректированный коэффициент множественной детерминации. Сравнить его с
нескорректированным (общим) коэффициентов детерминации.
С
помощью
–критерия Фишера оценить статистическую
надежность уравнения регрессии и коэффициента детерминации
С
помощью частных
–критериев Фишера оценить целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
.
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Решение
Для
удобства проведения расчетов поместим результаты промежуточных расчетов в
таблицу:
Найдем
средние квадратические отклонения признаков:
Расчет
парных коэффициентов корреляции и параметров линейного уравнения множественной
регрессии
1) Для
нахождения параметров линейного уравнения множественной регрессии:
необходимо
решить следующую систему линейных уравнений относительно неизвестных параметров
:
Решать систему уравнений
методом Крамера,
методом обратной матрицы или
методом Гаусса достаточно трудоемко, поэтому
воспользуемся готовыми формулами:
Рассчитаем
сначала парные коэффициенты корреляции:
Находим:
Таким
образом, получили следующее уравнение множественной регрессии:
Коэффициенты
стандартизированного уравнения регрессии
Коэффициенты
и
стандартизированного уравнения регрессии
находятся по формулам:
То есть
уравнение будет выглядеть следующим образом:
Так как
стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно
сказать, что ввод в действие новых основных фондов оказывает большее влияние на
выработку продукции, чем удельный вес рабочих высокой квалификации.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Коэффициенты
эластичности
Сравнивать
влияние факторов на результат можно также при помощи средних коэффициентов
эластичности:
Вычисляем:
Т.е.
увеличение только основных фондов (от своего среднего значения) или только
удельного веса рабочих высокой квалификации на 1% увеличивает в среднем
выработку продукции на 0,635% или 0,142% соответственно. Таким образом,
подтверждается большее влияние на результат
фактора
, чем фактора
.
Частные
и парные коэффициенты корреляции
2) Коэффициенты парной корреляции мы уже нашли:
Они
указывают на весьма сильную связь каждого фактора с результатом, а также
высокую межфакторную зависимость (факторы
и
явно коллинеарны, так как
). При такой сильной
межфакторной зависимости рекомендуется один из факторов исключить из
рассмотрения.
Частные
коэффициенты корреляции характеризуют тесноту связи между результатом и
соответствующим факторов при элиминировании (устранении влияния) других
факторов, включенных в уравнение регрессии.
При двух
факторах частные коэффициенты корреляции рассчитываются следующим образом:
Если
сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за
высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные
оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у
которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Коэффициенты
множественной корреляции и детерминации
Коэффициент
множественной корреляции определить по формуле:
Коэффициент
множественной корреляции показывает на весьма сильную связь всего набора
факторов с результатом.
3)
Нескорректированный коэффициент множественной детерминации
оценивает долю вариации результата за счет
представленных в уравнении факторов в общей вариации результата. Здесь эта доля
составляет 98,4% и указывает на высокую степень обусловленности вариации
результата вариацией факторов, иными словами – на весьма тесную связь факторов
с результатом.
Скорректированный
коэффициент множественной корреляции:
определяет
тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает
такую оценку тесноты связи, которая не зависит от числа факторов и поэтому
может сравниваться по разным моделям с разным числом факторов. Оба коэффициента
указывают на высокую (более 98%) детерминированность результата
в модели факторами
и
.
Надежность
уравнения регрессии. Критерий Фишера
4) Оценку
надежности уравнения регрессии в целом и показателя тесноты связи
дает
–критерий Фишера:
В нашем
случае фактическое значение
–критерия Фишера:
Получили,
что
(при
)
(по таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=2 и k2=20-2=18), то есть вероятность
случайно получить такое значение
– критерия не превышает допустимый уровень
значимости 5%. Следовательно, полученное значение не случайно, оно
сформировалось под влиянием существенных факторов, то есть подтверждается
статистическая значимость всего уравнения и показателя тесноты связи
.
5) С
помощью частных
–критериев Фишера оценим целесообразность
включения в уравнение множественной регрессии фактора
после
и фактора
после
при помощи формул:
Найдем
и
.
Получили,
что
. Следовательно, включение
в модель фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
Если
поменять первоначальный порядок включения факторов в модель и рассмотреть
вариант включения
после
, то результат расчета
частного
–критерия для
будет иным.
, то есть вероятность его
случайного формирования меньше принятого стандарта
. Следовательно, значение
частного
–критерия для дополнительно включенного
фактора
не случайно, является статистически значимым,
надежным, достоверным: прирост факторной дисперсии за счет дополнительного
фактора
является существенным.
Фактор
должен присутствовать в уравнении, в том числе
в варианте, когда он дополнительно включается после фактора
.
6) Общий
вывод состоит в том, что множественная модель с факторами
и
с
содержит неинформативный фактор
. Если исключить фактор
, то можно ограничится
уравнением парной регрессии:
The standardized coefficients in regression are also called beta coefficients and they are obtained by standardizing the dependent and independent variables. Standardization of the dependent and independent variables means that converting the values of these variables in a way that the mean and the standard deviation becomes 0 and 1 respectively. We can find the standardized coefficients of a linear regression model by using scale function while creating the model.
Example
Consider the below data frame −
Live Demo
> set.seed(99) > x<-rnorm(10,1.5) > y<-rnorm(10,2) > df1<-data.frame(x,y) > df1
Output
x y 1 1.7139625 1.2542310 2 1.9796581 2.9215504 3 1.5878287 2.7500544 4 1.9438585 -0.5085540 5 1.1371621 -1.0409341 6 1.6226740 2.0002658 7 0.6361548 1.6059810 8 1.9896243 0.2549723 9 1.1358831 2.4986315 10 0.2057580 2.2709538
Creating the regression model −
> Model1<-lm(y~x,data=df1) > summary(Model1)
Output
Call: lm(formula = y ~ x, data = df1) Residuals: Min 1Q Median 3Q Max -2.5458 -0.7047 0.1862 0.9178 1.7566 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.9635 1.2055 1.629 0.142 x -0.4034 0.7988 -0.505 0.627 Residual standard error: 1.453 on 8 degrees of freedom Multiple R-squared: 0.0309, Adjusted R-squared: -0.09024 F-statistic: 0.2551 on 1 and 8 DF, p-value: 0.6272
Creating the regression model for standardized coefficients −
> Model1_standardized_coefficients<-lm(scale(y)~scale(x),data=df1) > summary(Model1_standardized_coefficients)
Output
Call: lm(formula = scale(y) ~ scale(x), data = df1) Residuals: Min 1Q Median 3Q Max -1.8288 -0.5063 0.1338 0.6593 1.2619 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -3.701e-18 3.302e-01 0.000 1.000 scale(x) -1.758e-01 3.480e-01 -0.505 0.627 Residual standard error: 1.044 on 8 degrees of freedom Multiple R-squared: 0.0309, Adjusted R-squared: -0.09024 F-statistic: 0.2551 on 1 and 8 DF, p-value: 0.6272
Let’s have a look at another example −
Example
Live Demo
> y<-rnorm(10,2.5) > x1<-rnorm(10,0.2) > x2<-rnorm(10,0.5) > x3<-rnorm(10,1.5) > df2<-data.frame(x1,x2,x3,y) > df2
Output
x1 x2 x3 y 1 1.573053947 0.6329786 -0.07655243 3.598922 2 0.650256559 -1.1792643 2.12408260 3.252513 3 0.053706144 0.2215204 1.83022068 2.440583 4 0.328097240 -1.0524110 1.10187774 2.155431 5 -2.094720947 -0.8796993 0.41860307 2.722668 6 -1.166568921 -0.8570566 1.42307794 3.051786 7 0.002520447 -0.4211372 0.97446338 3.183643 8 0.268085782 -0.3668177 1.89128965 1.954121 9 0.290503410 2.1566444 0.81954674 1.132564 10 0.522759967 0.3449203 0.75130307 3.900052
> Model2_standardized_coefficients<- lm(scale(y)~scale(x1)+scale(x2)+scale(x3),data=df2) > summary(Model2_standardized_coefficients)
Output
Call: lm(formula = scale(y) ~ scale(x1) + scale(x2) + scale(x3), data = df2) Residuals: Min 1Q Median 3Q Max -1.4389 -0.5336 0.1917 0.3699 1.2726 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.577e-17 2.970e-01 0.000 1.000 scale(x1) 3.896e-01 3.415e-01 1.141 0.297 scale(x2) -6.845e-01 3.682e-01 -1.859 0.112 scale(x3) -4.808e-01 3.409e-01 -1.410 0.208 Residual standard error: 0.9392 on 6 degrees of freedom Multiple R-squared: 0.4119, Adjusted R-squared: 0.1179 F-statistic: 1.401 on 3 and 6 DF, p-value: 0.331