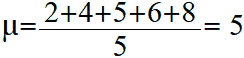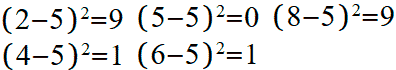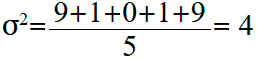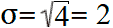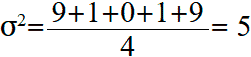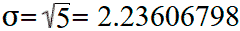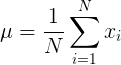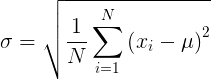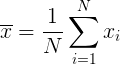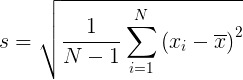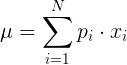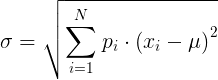Как найти стандартное отклонение онлайн

Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.

Как правило перечисленные термины равны квадратному корню дисперсии.

Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.

Cредняя оценка будет равна:

Вычисляем квадраты отклонений оценок от их средней оценки:

Вычислим среднее арифметическое (дисперсию) этих значений:

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:

Тогда стандартное отклонение будет равняться:

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Среднеквадратическое отклонение

begin{align}
& sigma=sqrt{frac{1}{n}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}

Стандартное отклонение

begin{align}
& s=sqrt{frac{n}{n-1}sigma^2}=sqrt{frac{1}{n-1}sum_{i=1}^N (x_i-bar{x})^2} \
end{align}

begin{align}
& где sigma^2-дисперсия; x_i-i-ый элемент выборки; n-объем выборки; bar{x}-среднее арифметическое выборки. \
end{align}

Калькулятор вычислит среднеквадратическое отклонение, а также стандартное отклонение и среднее арифметическое. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.

количество чисел

Калькулятор стандартного отклонения

Калькулятор стандартного отклонения (σ) со средним значением и дисперсией онлайн.

Калькулятор стандартного отклонения генеральной совокупности и выборки

Введите значения данных, разделенные запятыми (например: 3,2,9,4) или пробелами (например: 3 2 9 4), и нажмите кнопку « Рассчитать» .

Калькулятор стандартного отклонения дискретной случайной величины

Введите вероятность или вес и номер данных в каждой строке:

Расчет стандартного отклонения для всего населения

Средняя численность населения:

Стандартное отклонение населения:

Расчет стандартного отклонения выборочных данных

Выборочное среднее:

Стандартное отклонение выборки:

Расчет стандартного отклонения дискретной случайной величины

Среднее значение случайной величины:

Стандартное отклонение дискретной случайной величины:

Смотрите также

• Стандартное отклонение
• Калькулятор средневзвешенного значения
• Калькулятор отклонений
• Калькулятор GPA

Среднее квадратичное отклонение

Среднее квадратичное отклонение — это показатель рассеивания значений случайной величины относительно её математического ожидания.
Обозначается символом σ (греческая буква «сигма»).

Среднеквадратичное отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки
среднего арифметического,
при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

Чтобы найти среднеквадратичное отклонение, нужно взять квадратный корень из дисперсии:

Другими словами, среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.

Данный онлайн калькулятор поможет вычислить среднее квадратичное отклонение ряда значений.

Вводите каждое новое число в отдельную ячейку. Для добавления ячейки нажмите на кнопку со знаком «+».

Поделиться страницей в социальных сетях:

О калькулятор стандартного отклонения (Высокая точность)

Калькулятор стандартного отклонения используется для расчета среднего значения, дисперсии и стандартного отклонения набора чисел (Шаг за шагом).

стандартное отклонение

Стандартное отклонение — это мера изменчивости или разнообразия, широко используемая в статистике и теории вероятностей. Он показывает, насколько точны данные.

Стандартное отклонение — это квадратный корень из его дисперсии. Низкое стандартное отклонение указывает на то, что точки данных имеют тенденцию быть очень близкими к среднему значению, в то время как высокое стандартное отклонение указывает на то, что данные разбросаны по широкому диапазону значений.

Дисперсия и стандартное отклонение зависят от среднего значения набора чисел. Их вычисление зависит от того, является ли множество совокупностью или выборкой.

Вариация населения и стандартное отклонение

Стандартное отклонение населения измеряет изменчивость данных. Обычно это неизвестная константа. дисперсия населенияσ²и стандартное отклонение σ определяется как:

выборочная дисперсия и стандартное отклонение

Стандартное отклонение выборки — это оценка, основанная на стандартном отклонении совокупности выборки. выборочная дисперсия s²а стандартное отклонение s определяется как: