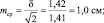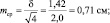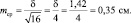2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал
Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:
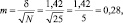
|
где δ – |
стандартное отклонение; |
|
N – |
число наблюдений или объем выборки, шт. |
Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 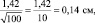
Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:
при объеме выборки N = 2 ошибка будет
при объеме выборки N = 4 ошибка будет
при объеме выборки N = 16 ошибка будет
Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 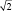
в 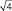
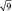
Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.
Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.
Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 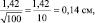
Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта
Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.
Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?
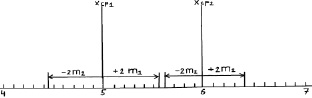
Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:
хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см
и
хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 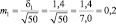
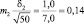
хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;
хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.
Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)
Снова вынесем эти пределы на график (рис. 2.2).
Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки
Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?
Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).
При выборках из 25 штук сеянцев, получаем две ошибки: 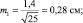
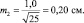
хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;
хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.
Выносим эти пределы опять на график (рис. 2.3).
Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)
Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-
1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-
1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-
1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-
1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?
To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?
The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something – i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?
The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,002,256 times.
Did this article help you?
Представление результатов исследования
В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.
Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.
Ошибка среднего арифметического
Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.
Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.
Ошибка среднего арифметического обозначается как m или
Ошибка среднего арифметического рассчитывается по формуле:
где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.
Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.
Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.
Правила записи результатов исследования
- В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
- В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
- В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.
Представление результатов научных исследований
В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52
В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).
Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)
| Эффективный модуль
упругости (Е), кПа |
Эффективный модуль
вязкости (V), Па с |
|||
| Этап
эксперимента |
Рассл. | Напряж. | Рассл. | Напряж. |
| До ФН | 7,0±0,3 | 17,1±1,4 | 29,7±1,7 | 46±4 |
| После ФН | 7,7±0,3 | 18,7±1,4 | 30,9±2,0 | 53±6 |
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-
1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-
2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-
3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-
4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-
5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-
6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-
1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-
1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 49 261 раз.
Была ли эта статья полезной?
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях: