Среднеквадрати́ческое отклонение (среднеквадрати́чное отклонение, стандартное отклонение[1]) — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.
В литературе обычно обозначают греческой буквой 
(сигма). В статистике принято два обозначения: — для генеральной совокупности и 
(с англ. standard deviation — стандартное отклонение) — для выборки.
Варианты определения[править | править код]
Обычно определяется как квадратный корень из дисперсии случайной величины: ![{displaystyle sigma ={sqrt {D[X]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c535aeb360aec0139028ee203973550bb364cbb)
. Измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.
В частности, если 
— 
-й элемент выборки, 
— объём выборки, 
— среднее арифметическое выборки (выборочное среднее — оценка математического ожидания величины):
,
то два основных способа оценки стандартного отклонения записываются нижеследующим образом.
Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[2]):
- .
Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.
Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии[2], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):
Само по себе, однако, 
не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.
Обе оценки являются состоятельными[2].
Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[3]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.
Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения[3][]:
Правило трёх сигм[править | править код]
Правило трёх сигм (
) гласит: вероятность того, что любая случайная величина отклонится от своего среднего значения менее чем на :
- .
Практически все значения нормально распределённой случайной величины лежат в интервале 
, где 
— математическое ожидание случайной величины. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.
Интерпретация[править | править код]
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, для у всех трёх числовых множеств: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение[править | править код]
На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.
Экономика и финансы[править | править код]
Среднее квадратическое отклонение доходности портфеля отождествляется с риском портфеля.
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.
Оценка рисков и критика[править | править код]
Среднеквадратическое отклонение широко распространено в финансовой сфере в качестве критерия оценки инвестиционного риска. По мнению американского экономиста Нассима Талеба, этого делать не следует. Так, по теории около двух третей изменений должны укладываться в определённые рамки (среднеквадратические отклонения −1 и +1) и что колебания свыше семи стандартных отклонений практически невозможны. Однако в реальной жизни, по мнению Талеба, всё иначе — скачки отдельных показателей могут превышать 10, 20, а иногда и 30 стандартных отклонений. Талеб считает, что риск-менеджерам следует избегать использования средств и методов, связанных со стандартными отклонениями, таких как регрессионные модели, коэффициент детерминации (R-квадрат) и бета-факторы. Кроме того, по мнению Талеба, среднеквадратическое отклонение — слишком сложный для понимания метод. Он считает, что тот, кто пытается оценить риск с помощью единственного показателя, обречён на неудачу[4].
Климат[править | править код]
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт[править | править код]
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Пример[править | править код]
Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.
Пусть оценки учеников класса следующие:
- .
Тогда средняя оценка равна:
- .
Вычислим квадраты отклонений оценок учеников от их средней оценки:
Среднее арифметическое этих значений называется дисперсией:
Стандартное отклонение равно квадратному корню дисперсии:
Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:
и стандартное отклонение равнялось бы:
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
Примечания[править | править код]
- ↑ Встречаются также различные синонимы: среднее квадратическое отклонение, стандартный разброс, стандартная неопределённость; термин «среднее квадратическое» означает «среднее степени 2»
- ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
- ↑ 1 2 C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — doi:10.1088/1674-1137/40/10/100001.
- ↑ Талеб, Гольдштейн, Шпицнагель, 2022, с. 46.
Литература[править | править код]
- Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..
- Нассим Талеб, Дениэл Гольдштейн, Марк Шпицнагель. Шесть ошибок руководителей компаний при управлении рисками // Управление рисками (Серия «Harvard Business Review: 10 лучших статей») = On Managing Risk / Коллектив авторов. — М.: Альпина Паблишер, 2022. — С. 41—50. — 206 с. — ISBN 978-5-9614-8186-0.
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение “xср” вместо “μ”.
Разница между формулами S и σ (“n” и “n–1”)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с “n–1”),
- полностью все данные – используется формула σ (с “n”).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 – μ = 15 – 20 = -5
x2 – μ = 26 – 20 = 6
x3 – μ = 15 – 20 = -5
x4 – μ = 24 – 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 – μ)² = (-5)² = 25
(x2 – μ)² = 6² = 36
(x3 – μ)² = (-5)² = 25
(x4 – μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi – μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле “=СТАНДОТКЛОНА(“
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
.
Принимая во внимание свойства
математического ожидания, легко показать
что
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное
.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
.
=9
=2,31.
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:
Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до
.
Решение:
Для нахождения коэффициента авоспользуемся свойством
.
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
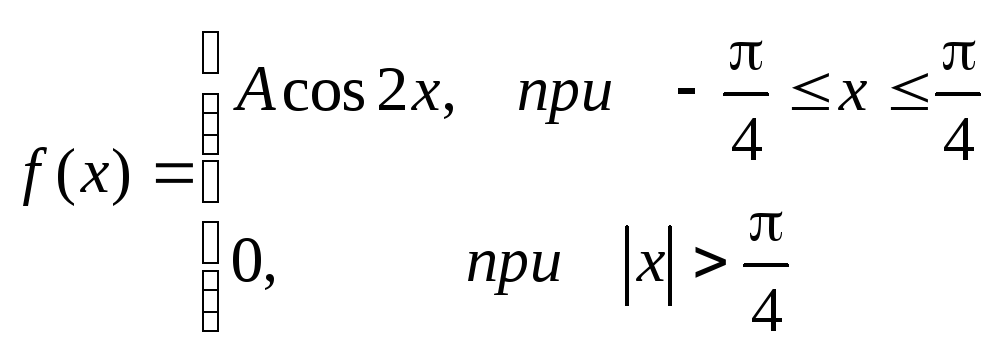
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал
.
Решение:
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке
:
2) На участке
3) На участке
Итого:
Найдем вероятность попадания случайной
величины в интервал
.
Ту же самую вероятность можно искать
и другим способом:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
1
Look at your data set. This is a crucial step in any type of statistical calculation, even if it is a simple figure like the mean or median.[2]
- Know how many numbers are in your sample.
- Do the numbers vary across a large range? Or are the differences between the numbers small, such as just a few decimal places?
- Know what type of data you are looking at. What do your numbers in your sample represent? this could be something like test scores, heart rate readings, height, weight etc.
- For example, a set of test scores is 10, 8, 10, 8, 8, and 4.
-
2
Gather all of your data. You will need every number in your sample to calculate the mean.[3]
- The mean is the average of all your data points.
- This is calculated by adding all of the numbers in your sample, then dividing this figure by the how many numbers there are in your sample (n).
- In the sample of test scores (10, 8, 10, 8, 8, 4) there are 6 numbers in the sample. Therefore n = 6.
Advertisement
-
3
Add the numbers in your sample together. This is the first part of calculating a mathematical average or mean.[4]
- For example, use the data set of quiz scores: 10, 8, 10, 8, 8, and 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. This is the sum of all the numbers in the data set or sample.
- Add the numbers a second time to check your answer.
-
4
Divide the sum by how many numbers there are in your sample (n). This will provide the average or mean of the data.[5]
- In the sample of test scores (10, 8, 10, 8, 8, and 4) there are six numbers, so n = 6.
- The sum of the test scores in the example was 48. So you would divide 48 by n to figure out the mean.
- 48 / 6 = 8
- The mean test score in the sample is 8.
Advertisement
-
1
Find the variance. The variance is a figure that represents how far the data in your sample is clustered around the mean.[6]
- This figure will give you an idea of how far your data is spread out.
- Samples with low variance have data that is clustered closely about the mean.
- Samples with high variance have data that is clustered far from the mean.
- Variance is often used to compare the distribution of two data sets.
-
2
Subtract the mean from each of your numbers in your sample. This will give you a figure of how much each data point differs from the mean.[7]
- For example, in our sample of test scores (10, 8, 10, 8, 8, and 4) the mean or mathematical average was 8.
- 10 – 8 = 2; 8 – 8 = 0, 10 – 8 = 2, 8 – 8 = 0, 8 – 8 = 0, and 4 – 8 = -4.
- Do this procedure again to check each answer. It is very important you have each of these figures correct as you will need them for the next step.
-
3
Square all of the numbers from each of the subtractions you just did. You will need each of these figures to find out the variance in your sample.[8]
- Remember, in our sample we subtracted the mean (8) from each of the numbers in the sample (10, 8, 10, 8, 8, and 4) and came up with the following: 2, 0, 2, 0, 0 and -4.
- To do the next calculation in figuring out variance you would perform the following: 22, 02, 22, 02, 02, and (-4)2 = 4, 0, 4, 0, 0, and 16.
- Check your answers before proceeding to the next step.
-
4
Add the squared numbers together. This figure is called the sum of squares.[9]
- In our example of test scores, the squares were as follows: 4, 0, 4, 0, 0, and 16.
- Remember, in the example of test scores we started by subtracting the mean from each of the scores and squaring these figures: (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- The sum of squares is 24.
-
5
Divide the sum of squares by (n-1). Remember, n is how many numbers are in your sample. Doing this step will provide the variance. The reason to use n-1 is to have sample variance and population variance unbiased. [10]
- In our sample of test scores (10, 8, 10, 8, 8, and 4) there are 6 numbers. Therefore, n = 6.
- n-1 = 5.
- Remember the sum of squares for this sample was 24.
- 24 / 5 = 4.8
- The variance in this sample is thus 4.8.
Advertisement
-
1
Find your variance figure. You will need this to find the standard deviation for your sample.[11]
- Remember, variance is how spread out your data is from the mean or mathematical average.
- Standard deviation is a similar figure, which represents how spread out your data is in your sample.
- In our example sample of test scores, the variance was 4.8.
-
2
Take the square root of the variance. This figure is the standard deviation.[12]
- Usually, at least 68% of all the samples will fall inside one standard deviation from the mean.
- Remember in our sample of test scores, the variance was 4.8.
- √4.8 = 2.19. The standard deviation in our sample of test scores is therefore 2.19.
- 5 out of 6 (83%) of our sample of test scores (10, 8, 10, 8, 8, and 4) is within one standard deviation (2.19) from the mean (8).
-
3
Go through finding the mean, variance and standard deviation again. This will allow you to check your answer.[13]
- It is important that you write down all steps to your problem when you are doing calculations by hand or with a calculator.
- If you come up with a different figure the second time around, check your work.
- If you cannot find where you made a mistake, start over a third time to compare your work.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
What is the standard deviation of 10 samples with a mean of 29.05?
Depends on the 10 samples of data. If all ten numbers were 29.05 then the standard deviation would be zero. Standard deviation is a measure of how much the data deviates from the mean.
-
Question
How do I calculate the standard deviation of 5 samples with the mean of 26?
You take the average of 26 and 5, divide by b squared and multiply by deviation equation constant.
-
Question
How do I find the standard deviation of 10 samples with a mean of 29.05?
Take each sample and subract the mean. Next, square each result, getting rid of the negative. Add the 10 results and divide the sun by 10 – 1 or 9. That is the standard deviation.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate standard deviation, start by calculating the mean, or average, of your data set. Then, subtract the mean from all of the numbers in your data set, and square each of the differences. Next, add all the squared numbers together, and divide the sum by n minus 1, where n equals how many numbers are in your data set. Finally, take the square root of that number to find the standard deviation. To learn how to find standard deviation with the help of example problems, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,555,320 times.
Reader Success Stories
-
“This article was the best statistics instructor I have ever been taught by. I have learned more from this little…” more
Did this article help you?
Числовые характеристики дискретной случайной величины
В этом разделе:
- Основная информация
- Онлайн калькулятор
- Полезные ссылки
Понравилось? Добавьте в закладки
Основная информация
Числовые характеристики дискретной случайной величины $X$, которые обычно требуется находить в учебных задачах по теории вероятностей, это математическое ожидание $M(X)$, дисперсия $D(X)$ и среднее квадратическое отклонение $sigma(X)$.
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
$$
sigma(X) = sqrt{D(X)}.
$$
Подробные формулы и примеры расчета вы найдете по ссылкам в предыдущем абзаце, в этом же разделе вы сможете автоматически и бесплатно рассчитать эти значения с помощью онлайн-калькулятора, который даст не только ответ, но и продемонстрирует процесс вычисления.
Подробно решим ваши задачи по теории вероятностей
Калькулятор: числовые характеристики случайной величины
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -1.5 или 10.558). Введите нужные значения (убедитесь, что сумма вероятностей равна единице, то есть закон распределения задан верно).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет процесс вычисления математического ожидания $M(X)$, дисперсии $D(X)$ и СКО $sigma(X)$.
- Нужны еще расчеты? Вводите новые числа и нажимайте на кнопку.
Видео. Полезные ссылки
Видеоролики об СКО
На закуску для продвинутых – какие формулы вычисления СКО для выборок бывают и для чего подходят.
Лучшее спасибо – порекомендовать эту страницу
Полезные ссылки
- Калькуляторы по теории вероятнстей
- Онлайн учебник по ТВ
- Примеры решений по теории вероятностей
- Контрольные по теории вероятностей на заказ
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
