Как найти стандартное отклонение в процентах

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ (“n” и “n–1”)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с “n–1”),
• полностью все данные – используется формула σ (с “n”).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 – μ = 15 – 20 = -5

x2 – μ = 26 – 20 = 6

x3 – μ = 15 – 20 = -5

x4 – μ = 24 – 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 – μ)² = (-5)² = 25

(x2 – μ)² = 6² = 36

(x3 – μ)² = (-5)² = 25

(x4 – μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi – μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi – μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi – μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это “среднее квадратов отклонений от среднего”. Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с “n – 1” в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле “=СТАНДОТКЛОНА(“

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при <10% выборка слабо вариабельна,
• при 10% – 20 % — средне вариабельна,
• при >20 % — выборка сильно вариабельна.

Узнайте также про:

• Корреляции,
• Метод Крамера,
• Метод наименьших квадратов,
• Теорию вероятностей
• Интегралы.

Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений.

Второй подход к расчету отклонений состоит в их возведении в квадрат.

Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:

• Дисперсия определяется как среднее квадратов отклонений от среднего значения.
• Стандартное отклонение – это положительный квадратный корень дисперсии.

Далее обсуждается расчет и использования дисперсии и стандартного отклонения.

Дисперсия генеральной совокупности.

Если нам известен каждый элемент генеральной совокупности, мы можем вычислить дисперсию генеральной совокупности или просто дисперсию (англ. ‘population variance’).

Она обозначается символом (sigma^2)[сигма] и представляет собой среднее арифметическое квадратов отклонений от среднего значения.

Формула дисперсии генеральной совокупности.

Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех (N) элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на (N).

Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.

Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.

---

Рассмотрим пример.

Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2.0%.

Следовательно, дисперсия прибыли в процентах от выручки составляет:

(1/3)[(0.9 – 2.0)² + (1.6 – 2.0)² + (3.5 – 2.0)²]
= (1/3)(-1.1² + -0.4² + 1.5²)
= (1/3)(1.21 + 0.16 + 2.25) = (1/3)(3.62) = 1.21

Стандартное отклонение генеральной совокупности.

Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.

Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.

Формула стандартного отклонения генеральной совокупности.

Стандартное отклонение генеральной совокупности (или просто стандартное отклонение, а также среднеквадратическое отклонение, от англ. ‘population standard deviation’), определяемое как положительный квадратный корень из дисперсии генеральной совокупности, составляет:

Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: ( sqrt{1.21} ) = 1.10.

Как дисперсия, так и стандартное отклонение являются примерами параметров распределения. В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.

Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.

Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12.

Мы обсудим эти вычисления далее.

Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12, как в следующем примере.

Пример расчета стандартного отклонения для генеральной совокупности.

В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.

Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.

Критериями являются:

• сохранение капитала (эффективность на медвежьем рынке),
• непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,
• доступность (дисквалификация фондов, которые закрыты для новых инвесторов), и
• долгосрочные показатели эффективности после уплаты налогов.

Оборачиваемость или оборот портфеля, показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.

Таблица 20. Оборот портфеля: взаимные фонды Forbes Honor Roll за 2013 год.

Фонд	Годовой оборот портфеля (%)
Bruce Fund (BRUFX)	10
CGM Focus Fund (CGMFX)	360
Hotchkis And Wiley Small Cap Value A Fund (HWSAX)	37
Aegis Value Fund (AVALX)	20
Delafield Fund (DEFIX)	49
Homestead Small Company Stock Fund (HSCSX)	1
Robeco Boston Partners Small Cap Value II Fund (BPSCX)	32
Hotchkis And Wiley Mid Cap Value A Fund (HWMAX)	72
T Rowe Price Small Cap Value Fund (PRSVX)	9
Guggenheim Mid Cap Value Fund Class A (SEVAX)	19
Wells Fargo Advantage Small Cap Value Fund (SSMVX)	16
Stratton Small-Cap Value Fund (STSCX)	11

Источник: Forbes (2013).

Основываясь на данных из таблицы 20, сделайте следующее:

1. Рассчитайте среднее по совокупности для оборота портфеля за период, используя данные для 12 фондов из Honor Roll.
2. Рассчитайте дисперсию и стандартное отклонение совокупности для оборота портфеля.
3. Объясните использование формул в этом примере.

---

Решение для части 1:

(mu) = (10 + 360 + 37 + 20 + 49 + 1 + 32 + 72 + 9 + 19 + 16 + 11)/12
= 636 /12 = 53%.

---

Решение для части 2:

Установив, что (mu) = 53%, мы можем вычислить дисперсию

( sigma^2 = { sum_{i=1}^{N} ( X_i – mu )^2 over N } ), сначала рассчитав числитель, а затем разделив результат на (N) = 12.

Числитель (сумма квадратов отклонений от среднего) равен:

(10 – 53)² + (360 – 53)² + (37 – 53)² + (20 – 53)² +
(49 – 53)² + (1 – 53)² + (32 – 53)² + (72 – 53)² +
(9 – 53)² + (19 – 53)² + (16 – 53)² + (11 – 53)² = 107,190

Таким образом,

( sigma^2 ) = 107,190/12 = 8,932.50.

Для расчета стандартного отклонения находим квадратный корень:

( sigma = sqrt{ 8,932.50 } ) = 94.51%.

Единицей измерения дисперсии является процент в квадрате, поэтому единицей измерения стандартного отклонения также является процент.

---

Решение для части 3:

Если генеральная совокупность четко определена как фонды Forbes Honor Roll за один конкретный год (2013 г.), и если под оборотом портфеля понимается конкретный одногодичный период, о котором отчитывается Forbes, то применение формул генеральной совокупности для дисперсии и стандартного отклонения уместно.

Результаты 8,932.50 и 94.51 представляют собой, соответственно, перекрестную дисперсию и стандартное отклонение годового оборота портфеля для фондов Forbes Honor Roll за 2013 год.

Фактически, мы не могли должным образом использовать фонды Honor Roll для оценки дисперсии оборота портфеля (например) любой другой по-разному определенной генеральной совокупности, потому что фонды Honor Roll не являются случайной выборкой из какой-либо большей генеральной совокупности взаимных фондов США.

Выборочная дисперсия.

Во многих случаях в управлении инвестициями подгруппа или выборка из генеральной совокупности – это все, что мы можем наблюдать. Когда мы имеем дело с выборками, сводные показатели называются статистикой.

Статистика, которая измеряет дисперсию по выборке, называется выборочной дисперсией или дисперсией выборки (англ. ‘sample variance’).

В приведенном ниже обсуждении обратите внимание на использование латинских букв вместо греческих для обозначения объема выборки.

Формула выборочной дисперсии.

Формула 13 предписывает нам предпринять следующие шаги для вычисления выборочной дисперсии:

1. Рассчитать выборочное среднее значение, ( overline X ).
2. Рассчитать квадратичное отклонение каждого наблюдения от среднего значения по выборке, ( ( X_i – overline X )^2 )
3. Найти сумму квадратов отклонений от среднего: ( sum_{i=1}^{n} ( X_i – overline X )^2 ).
4. Разделить сумму квадратов отклонений от среднего на ( (n – 1)).

Мы проиллюстрируем расчет выборочной дисперсии и выборочного стандартного отклонения на примере ниже.

Отличие выборочной дисперсии от дисперсии генеральной совокупности.

Мы используем обозначение ( s^2 ) для выборочной дисперсии, чтобы отличить ее от дисперсии генеральной совокупности ( sigma^2 ).

Формула для выборочной дисперсии почти такая же, как и для дисперсии генеральной совокупности, за исключением использования среднего значения выборки ( overline X ) вместо среднего значения генеральной совокупности μ и другого делителя.

В случае дисперсии генеральной совокупности мы делим числитель на размер совокупности (N). Однако для дисперсии выборки мы делим ее на размер выборки минус 1 или (n – 1). Используя (n – 1) (а не (n)) в качестве делителя мы улучшаем статистические свойства выборочной дисперсии.

В статистических терминах выборочная дисперсия, определенная в Формуле 13, является несмещенной оценкой (англ. ‘unbiased estimator ‘) дисперсии генеральной совокупности ( sigma^2 ).

Мы обсудим эту концепцию далее в чтении о выборке.

Величина (n – 1) также называется числом степеней свободы (англ. ‘number of degrees of freedom’) при оценке дисперсии генеральной совокупности.

Чтобы оценить дисперсию ( s^2 ), мы должны сначала вычислить среднее. После того как мы вычислили среднее значение выборки, существует только (n – 1) независимых отклонений от него.

Стандартное отклонение выборки.

Для стандартного отклонения генеральной совокупности мы аналогичным образом можем вычислить стандартное отклонение выборки, взяв квадратный корень из положительной дисперсии выборки.

Формула стандартного отклонения выборки.

Стандартное отклонение выборки (выборочное стандартное отклонение, выборочное среднеквадратическое отклонение, англ. ‘sample standard deviation’), обозначается символом (s) и рассчитывается следующим образом:

Чтобы рассчитать стандартное отклонение выборки, мы сначала вычисляем дисперсию выборки, используя приведенные выше шаги. Затем мы берем квадратный корень из выборочной дисперсии.

Пример, приведенный ниже, иллюстрирует расчет выборочной дисперсии и стандартного отклонения выборки для двух взаимных фондов, представленных ранее.

Пример расчета выборочной дисперсии и стандартного отклонения выборки.

После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см.  Пример расчета размаха и среднего абсолютного отклонения для оценки риска).

Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.

Таблица 15. Совокупная доходность двух взаимных фондов,
2008-2012 гг. (повтор).

Год	Фонд Selected American Shares (SLASX)	Фонд T. Rowe Price Equity Income (PRFDX)
2008	-39.44%	-35.75%
2009	31.64	25.62
2010	12.53	15.15
2011	-4.35	-0.72
2012	12.82	17.25

Источник: performance.morningstar.com.

На основании приведенных выше данных сделайте следующее:

1. Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
2. Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
3. Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.

---

Решение для части 1:

Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).

А. SLASX:

1. Среднее значение выборки:

( overline R ) = (-39.44 + 31.64 + 12.53 – 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.

2. Квадратичные отклонения от среднего значения:

(-39.44 – 2.64)² = (-42.08)² = 1,770.73
(31.64 – 2.64)² = (29.00)² = 841.00
(12.53 – 2.64)² = (9.89)² = 97.81
(-4.35 – 2.64)² = (-6.99)² = 48.86
(12.82 – 2.64)² = (10.18)² = 103.63

3. Сумма квадратов отклонений от среднего составляет:

1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.

4. Разделим сумму квадратов отклонений от среднего на (n – 1):

2,862.03 / (5 – 1) = 2,862.03 / 4 = 715.51

B. PRFDX:

1. Среднее значение выборки:

( overline R ) = (-35.75 + 25.62 + 15.15 – 0.72 + 17.25)/5 = 21.55/5 = 4.31%.

2. Квадратичные отклонения от среднего значения:

(-35.75 – 4.31)² = (-40.06)² = 1,604.80
(25.62 – 4.31)² = (21.31)² = 454.12
(15.15 – 4.31)² = (10.84)² = 117.51
(-0.72 – 4.31)² = (-5.03)² = 25.30
(17.25 – 4.31)² = (12.94)² = 167.44

3. Сумма квадратов отклонений от среднего составляет:

1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.

4. Разделим сумму квадратов отклонений от среднего на ((n – 1)):

2,369.17/4 = 592.29

---

Решение для части 2:

Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.

---

Решение для части 3:

Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.

Таблица 21. Два взаимных фонда: сравнение стандартного отклонения и среднего абсолютного отклонения (MAD).

Фонд	Стандартное отклонение (%)	Среднее абсолютное отклонение (%)
SLASX	26.7	19.6
PRFDX	24.3	18.0

Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат).

Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем  среднее арифметическое и стандартное отклонение вместе при анализе данных.

Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.

---

В Таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.

Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.

Таблица 22. Доходность рынка ценных бумаг: средние значения и стандартные отклонения.

Ставка доходности	Геометрическое среднее (%)	Среднее арифметическое (%)	Стандартное отклонение
S&P 500 (Годовая)	9.84	11.82	20.18
S&P 500 (Месячная)	0.79	0.94	5.50

Источник: Ibbotson.

Как работает стандартное отклонение в Excel

Добрый день!

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.

Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

• Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

Теперь создадим файл примера и на его основе рассмотрим работу этой функции. Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц. Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода. Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4). Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты. Получаем такую таблицу: Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно. Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

С возрастом желание заработать переходит в желание сэкономить.
Михаил Жванецкий

Как рассчитать процент отклонения факта от плана?

Как посчитать процент отклонения факта от плана?

Расчёт показателей, позволяющих определить, на сколько выполнен план, очень важен.

Если отклонение от плана слишком большое, то это может сильно повлиять на бюджет организации — возникнет необходимость принимать соответствующие меры.

Итак, как найти процент отклонения от плана?

Как известно, отклонение бывает двух видов — абсолютное и относительное.

Абсолютное отклонение представляет собой разницу между 2 показателями (плановым и фактическим, базовым и расчётным). Это числовая величина.

Относительное отклонение — это отношение между 2 показателями в процентах.

Так как речь идёт о проценте отклонения, то будем пользоваться формулой относительного отклонения.

Процент отклонения факта от плана рассчитывается для заданного отчётного периода — месяц, квартал, год.

1) Pi — плановые показатели по продукции / услуге / виду деятельности i.

2) Fi — фактические показатели.

В качестве базового показателя берём план, в качестве текущего показателя — факт.

Отклонение в процентах будет рассчитываться по формуле:

Oo = (Fi / Pi) * 100% — 100%

Другой вид формулы:

Oo = (Fi / Pi — 1) * 100%

Ещё можно воспользоваться такой формулой:

Oo = ((Fi — Pi) / Pi) * 100%

При этом возможны несколько ситуаций:

1) Oo > 0 — план перевыполнен.

2) Oo = 0 — плановые показатели были достигнуты.

Пример

Предприятие работает в целлюлозно-бумажной отрасли. Имеются плановые и фактические показатели по выпуску (в тоннах) различных видов бумаги за 1 квартал 2017 года.

Нужно найти процент отклонения факта от плана.

Для каждого вида продукции делим значения «факт» на значения «план», вычитаем единицу и переводим в проценты.

По 1 и 2 показателю план не выполнен. По 3 показателю план перевыполнен.

По сути, одно из основных направлений в работе экономиста — это планирование, сбор фактической информации и проведение сравнительного анализа для оптимизации расходов предприятия.

Отклонения принято рассчитывать, как абсолютные, так и относительные.

В формулировке вопроса имеется в виду расчёт относительных отклонений.

Относительное отклонение в результате даёт процент отклонения Факта от Плана.

Вообще, на своей практике встречался с двумя вариантами расчёта.

В первом варианте относительное отклонение рассчитывается, как

Результат расчёта можно наблюдать на рисунке ниже.

Полученное отклонение показывает на сколько процентов выполнен План, то есть 100% будет идеальным значением, когда фактические данные будут полностью соответствовать плановым. Если значение меньше 100%, то План недовыполнили, если больше — перевыполнили.

Второй способ расчёта практически отражает первый, только полученное значение вычитается из 100%, то есть формула расчёта относительного отклонения во втором случае будет следующей

100-(Факт/План)*100, либо (План-Факт)/План*100

Результат данного расчёта можно наблюдать также на рисунке ниже.

При данном варианте расчёта мы видим на сколько процентов произошло отклонение от Плана. Таким образом 0% показывает соответствие Факта Плану, отрицательное значение говорит о перевыполнении Плна, а положительное — недовыполнении.

При расчёте Абсолютного отклонения всё гораздо проще.

Таким образом, мы сможем увидеть абсолютное отклонение Факта от Плана. Если значение равно 0, то Факт равен Плану, если получаем положительное значение, то произошло перевыполнение Плана, отрицательное — недовыполнение.

Бывает отставание фактических показателей от плановых, а бывает перевыполнение плана. В обоих случаях требуется рассчитать процент отклонения факта от плана.

Проще всего работать с конкретными цифрами. Например, завод должен был произвести 150 автомобилей, а выпустил 175 шт. На сколько процентов перевыполнен план?

Можно построить пропорцию:

х = 175*100/150 = 116,67%

Процент отклонения факта от нормы 116,67% — 100% = 16,67%

Или сначала посчитаем, что завод выпустил «лишние» 25 авто (175-150),

а потом составляем пропорцию:

у = 25*100 / 150 = 16,67%.

Ещё проще воспользоваться возможностями таблицы excel:

Часто требуется рассчитать процент отклонения факта от плана в excel.

Составляем таблицу, состоящую из 4-х столбиков:

Наименование показателя, план, факт и процент отклонения.

Формула для расчета процента отклонения факта от плана приведена на рисунке выше.

Можно записать как =ОКРУГЛ(B3/A3*100;2) или =ОКРУГЛ(B3/A3*100-10­ 0;2)

В зависимости от того, какие вам показатели нужны, абсолютные или относительные.

Если у нас есть таблица, в которой занесены все данные, т.е. прописан определенный показатель, и даны исходные данный (в виде план и факт), тогда высчитать процент отклонения не составит труда.

Не стоит забывать, что отклонение есть абсолютное и относительное.

Мы высчитывает относительное отклонение, подставляя данные в формулу

Факт :(делим) на План х(умножаем) 100%

Чтобы было более понятно приведем пример. Для этого найдем таблицу:

Высчитываем первый показатель «Товарная продукция»

936,5 : 982,1 х 100% = 0,95 х 100% = 95%

Получается, что план был не выполнен в полном объеме, так как показатель менее 100%.

Если после высчитывания получится 100%, значит план полностью выполнен.

А если будет более 100%, значит перевыполнен.

Так как вопрос о проценте отклонения, то речь идет об относительном отклонении факта от плана, но мы посчитаем в нашем примере и абсолютное отклонение.

Допустим, мы запланировали выпустить в 2018 году 120 единиц продукции, а выпустили фактически — 130 единиц. Процент отклонения факта от плана считается так: факт поделить на план, умножить на 100, и вычесть из полученного результата 100.

Считаем: 130 / 120 = 1,083, умножаем на 100, получается 108,3, вычитаем 100 = 8,3 %

Отклонение равно 8,3 %. Так как мы получили положительный результат, то речь идет о перевыполнении плана на 8,3 процентов, если бы результат был отрицательным, то план был бы недовыполнен. Абсолютное же отклонение считается вообще очень просто — от факта отнимается план, в нашем случае это 130-120 = 10 единиц продукции, план перевыполнен на 10 единиц продукции.

С этим вопросом сталкиваются экономисты многих предприятий, особенно когда нужно предоставить начальству расчет. Лучше всего рассмотреть на примере:

Например, нам нужно выпустить 1000 единиц продукции, но по факту предприятие выпустило 900 единиц продукции. Чтобы узнать насколько выполнен план, необходимо будет фактическое значение на планируемое значение и умножить на 100 процентов.

Итак, получаем 900/1000*100 = 90%. Значит план был выполнен только на девяносто процентов.

В данном примере, который представлен в ответе выше, предприятие не смогло выполнить план на десять процентов.

Такие задачки лучше всего решать в Экселе.

Для того, чтобы понимать на сколько процентов отличается факт от плана нужно воспользоваться простой формулой рассчёта, которая представлена ниже:

(Ф ÷ П) • 100, где в формуле

Рассмотрим на примере для большей наглядности.

Фабрика по пошиву одежды должна была сшить по плану 300 рабочих комбинезонов, но за отведенный срок сшили всего 250 комбинезонов. Производим рассчёт.

250 ÷ 300 = 0,83 • 100 = 83,33 %

Получается, что план не был выполнен на 100 %, а лишь 83,33 %.

Поменяем значения в задаче: П = 250, Ф = 300.

300 ÷ 250 = 1,2 • 100 = 120 %.

Получается, что план был перевыполнен на 20 %.

Посчитать процент отклонения не так и сложно.

Чтобы было проще можно объяснить на примере.

Производство должно было выпустить за одни месяц 200 000 книг, а выпустили только 180000.

Факт делим на план и умножаем на 100%.

Теперь высчитываем 100%-90%=10% — наш план не выполнили на 10%, это и есть показатель недовыполнения.

Теперь посчитаем, если мы план перевыполнили.

План составляет 200000 книжек, мы выпустили 210000.

Таким образом перевыполнение плана равняется 5%.

Почему-то проценты у многих вызывают сложности. Много раз наблюдал, как на уроках даже те, у кого с остальными темами все в порядке, столкнувшись с процентами и долями начинают «буксовать». И почему-то у учителей не получалось понять, из-за чего тема процентов вызывает такие проблемы и как её объяснять. Впрочем, непонимание процентов выражается хотя бы в распространенных выражениях типа «это гарантировано на 120%» или «я выложился на 200%». Прежде всего очень важно осознать, что 100% — это основа, норма. 100% — это всё, что есть или должно быть. То есть нельзя гарантировать что-то больше, чем на 100%, и нельзя усилий приложить на 200%, так как все ваши возможные усилия и гарантии составляют эту основу, эти 100%.

В примере про план и факт за план берется 100%. Это — наша основа, норма, и нам надо понять, насколько этот план выполнен. В случае с планом может быть и 98%, и 134%, так как технически можно выпустить больше продукции, чем запланировано.

Чтобы узнать, насколько выполнен план, нам необходимо знать цифры плана и факта и сравнить их. Из этих цирф делаем два простых и понятных уравнения:

Со школы в наших головах должно было отпечататься, что такие системы составляются в одно уравнение крест-накрест, то есть мы берем диагонали: (план) и (Х) и (факт) и (100%):

Посчитать отклонение в Excel

Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Урок: Формула среднего квадратичного отклонения в Excel

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.

1. Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».

Урок: Как посчитать среднее значение в Excel

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Как посчитать проценты в Excel

Мы сталкиваемся с процентами не только на работе или учебе, но и в нашей повседневной жизни – скидки, чаевые, депозитные ставки, кредиты и прочее. Поэтому умение работать с процентами будет полезно в разных сферах жизни. В этой статье мы ближе познакомимся с процентами, и рассмотрим, как быстро посчитать проценты в Excel, а также на примерах разберем следующие вопросы:

• как посчитать проценты в Excel формула;
• как посчитать процент от числа в Excel;
• как посчитать проценты от суммы в Excel;
• посчитать разницу в процентах Excel;

Как посчитать проценты в Excel формула

Прежде чем перейти к вопросу подсчета процентов в Excel, давайте вспомним основные знания о процентах. Процент – это сотая часть единицы. Из школьной программы вы наверняка знаете, что для того чтобы посчитать проценты, необходимо разделить искомую часть на целое и умножить на 100. Таким образом формула расчёта процентов выглядит следующим образом:

Посчитать проценты в Excel намного проще, так как вычисление некоторых математических операций в Excel происходит автоматически. Поэтому формула расчета процентов в Excel преобразуется следующим образом:

Для того чтобы посчитать проценты в Excel нет необходимости умножать результат на 100, если для ячейки используется Процентный формат.

Рассмотрим наглядный пример, как посчитать процент выполнения плана в Excel. Пусть у нас есть таблица с данными о запланированном объеме реализации продукции и фактическом объеме.

Как посчитать проценты в Excel – Исходные данные для расчета процентов

Для того чтобы посчитать процент выполнения плана необходимо:

• В ячейке D2 ввести формулу =C2/B2 и скопировать ее в остальные ячейки с помощью маркера заполнения.
• На вкладке « Главная » в группе « Число » выбрать «Процентный формат» для отображения результатов в формате процентов.

В результате мы получаем значения, округленные до целых чисел, которые показывают процент выполнения плана:

Как посчитать проценты в Excel – Процент выполнения плана

Следует отметить, что универсальной формулы, как посчитать проценты нет. Все зависит от того, что вы хотите получить в результате. Поэтому в этой статье мы рассмотрим примеры формул вычисления процента от числа, от общей суммы, прироста в процентах и многое другое.

Как посчитать процент от числа в Excel

Для того, чтобы посчитать процент от числа, необходимо использовать следующую формулу:

Рассмотрим пример расчета процента от числа. У нас есть таблица со стоимостью товаров без НДС и ставкой НДС для каждого товара.

Как посчитать проценты в Excel – Исходные данные для расчета процента от числа

Примечание : если вы вручную вводите в ячейке числовое значение и после него ставите знак %, то Excel применяет к данной ячейке процентный формат и воспринимает это число как его сотую часть. Например, если в ячейку ввести 18%, то для расчётов Excel будет использовать значение 0,18.

Пусть нам необходимо рассчитать НДС и стоимость продуктов с налогом на добавленную стоимость.

• Для того чтобы посчитать НДС в денежном эквиваленте, т.е. посчитать процент от числа в ячейке D2 вводим формулу =B2*C2 и заполняем остальные ячейки.
• В ячейке E2 суммируем ячейки B2 и D2 , для того чтобы получить стоимость с НДС.

В результате получаем следующие данные расчета процента от числа:

Как посчитать проценты в Excel – Процент от числа в Excel

Как посчитать проценты от суммы в Excel

Рассмотрим пример, когда нам необходимо посчитать проценты от суммы по каждой позиции. Пусть у нас есть таблица продаж некоторых видов продуктов с итоговой суммой. Нам необходимо посчитать проценты от суммы по каждому виду товара, то есть посчитать в процентном соотношении сколько выручки приносит каждый товар от общей суммы.

Как посчитать проценты в Excel – Исходные данные для расчета процентов от суммы

Для этого проделываем следующее:

• В ячейке C2 вводим следующую формулу: =B2/$B$9 . Для ячейки B9 мы используем абсолютную ссылку (со знаками $), чтобы она была неизменной, а для ячейки B2 – относительную, чтобы она изменялась при копировании формулы в другие ячейки.
• Используя маркер заполнения копируем эту формулу расчета процентов от суммы для всех значений.
• Для отображения результатов в формате процентов, на вкладке « Главная » в группе « Число », задаем «Процентный формат» с двумя знаками после запятой.

В результате мы получаем следующие значения процентов от суммы:

Как посчитать проценты в Excel – Проценты от суммы в Excel

Посчитать разницу в процентах Excel

Для того чтобы посчитать разницу в процентах, необходимо использовать следующую формулу:

где А – старое значение, а B – новое.

Рассмотрим пример, как посчитать разницу в процентах. Пусть у нас есть данные о продажах за два года. Нам необходимо определить процентное изменение продаж в отчетном году, по сравнению с предыдущим.

Как посчитать проценты в Excel – Исходные данные для расчета разницы в процентах

Итак приступим к расчетам процентов:

• В ячейке D2 вводим формулу =(C2-B2)/B2 .
• Копируем формулу в остальные ячейки, используя маркер заполнения.
• Применяем процентный формат для результирующих ячеек.

В результате у нас получается следующая таблица:

Как посчитать проценты в Excel – Вычисление разницы в процентах

В нашем примере положительные данные показывают прирост в процентах, а отрицательные значения – уменьшение в процентах.

Теперь вы знаете, как посчитать проценты в Excel, например, как посчитать процент от числа, проценты от общей суммы и прирост в процентах.

Как посчитать процент отклонения в Excel по двум формулам

Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?

Как посчитать отклонение в процентах в Excel

Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.

Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.

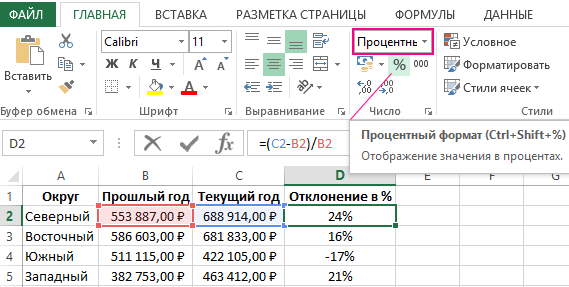
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.

Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.

Альтернативная формула для вычисления процента отклонения в Excel

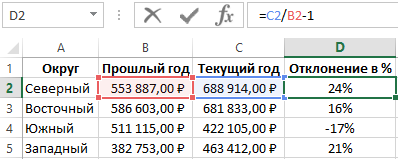
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.

Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.

Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.

Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.