Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции Функция СТАНДОТКЛОН.В.
Синтаксис
СТАНДОТКЛОН(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.
-
Стандартное отклонение вычисляется с использованием “n-1” метода.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
-
Функция СТАНДОТКЛОН вычисляется по следующей формуле:
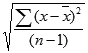
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОН(A3:A12) |
Стандартное отклонение предела прочности (27,46392) |
27,46392 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
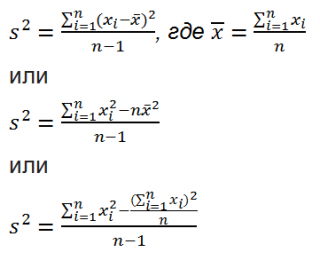
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
Для вычисления дисперсии выборки нужно:
- вычислить среднее значение выборки;
-
вычислить “расстояния” от каждого значения до среднего (x
i
-x
ср.
); - возвести “расстояния” в квадрат, чтобы отклонения в разные стороны от среднего не компенсировали друг друга;
- вычислить среднее значение квадратов “расстояний”)
Примечание
: в знаменателе формулы стоит n-1, а не n т.к. дисперсия выборки – это оценка дисперсии случайной величины (вычитаем 1, чтобы оценка была несмещенной).
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
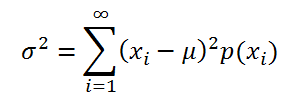
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
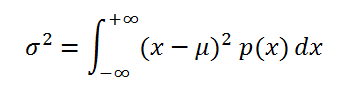
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент – числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х – случайная величина, а – константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y – случайные величины, Cov(Х;Y) – ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия – среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
– это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
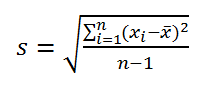
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) – отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
– ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
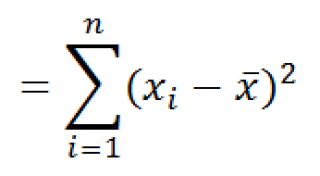
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
– ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
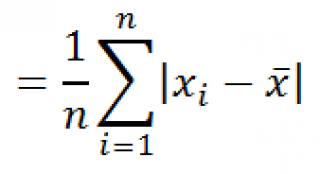
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
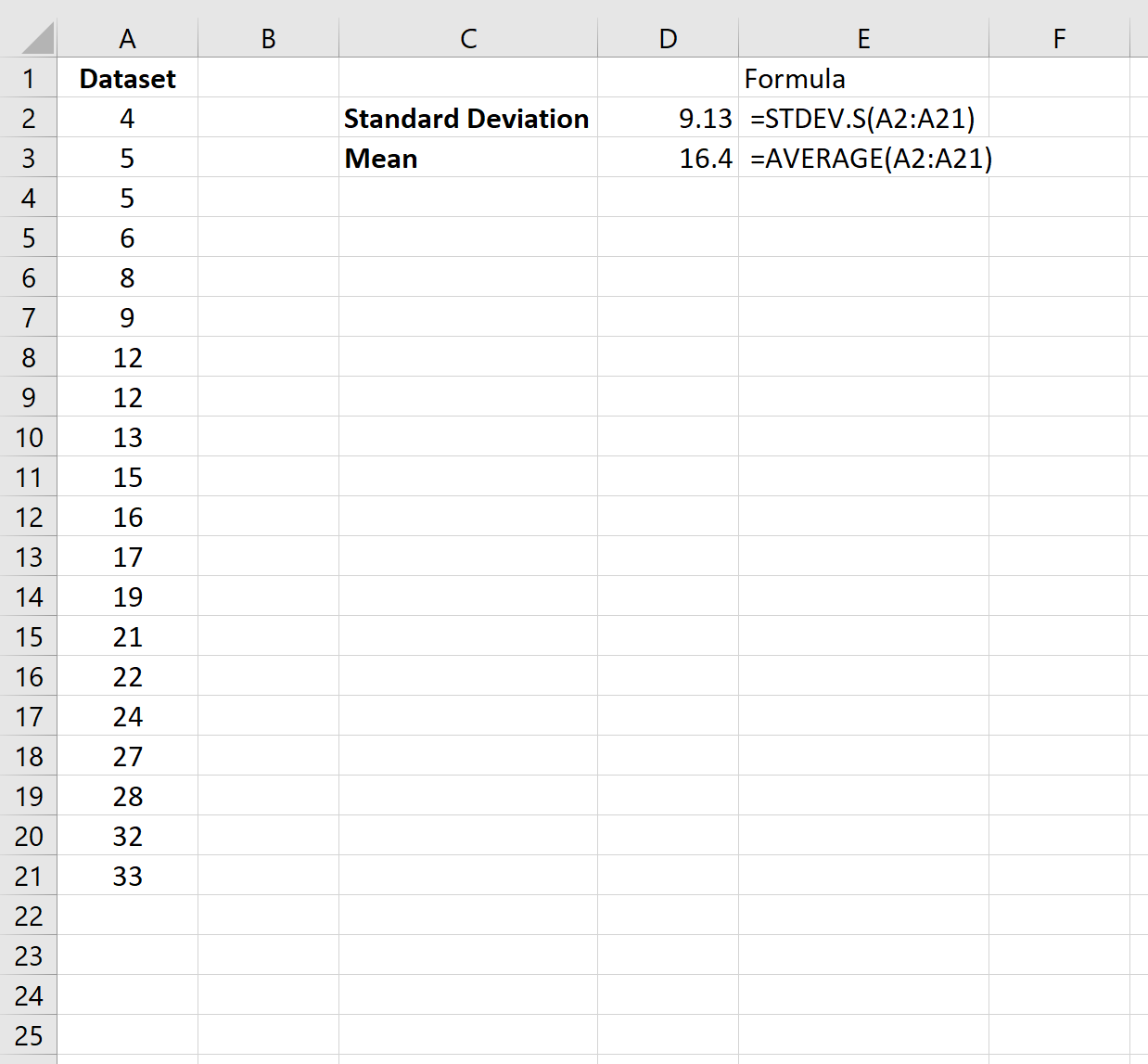
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
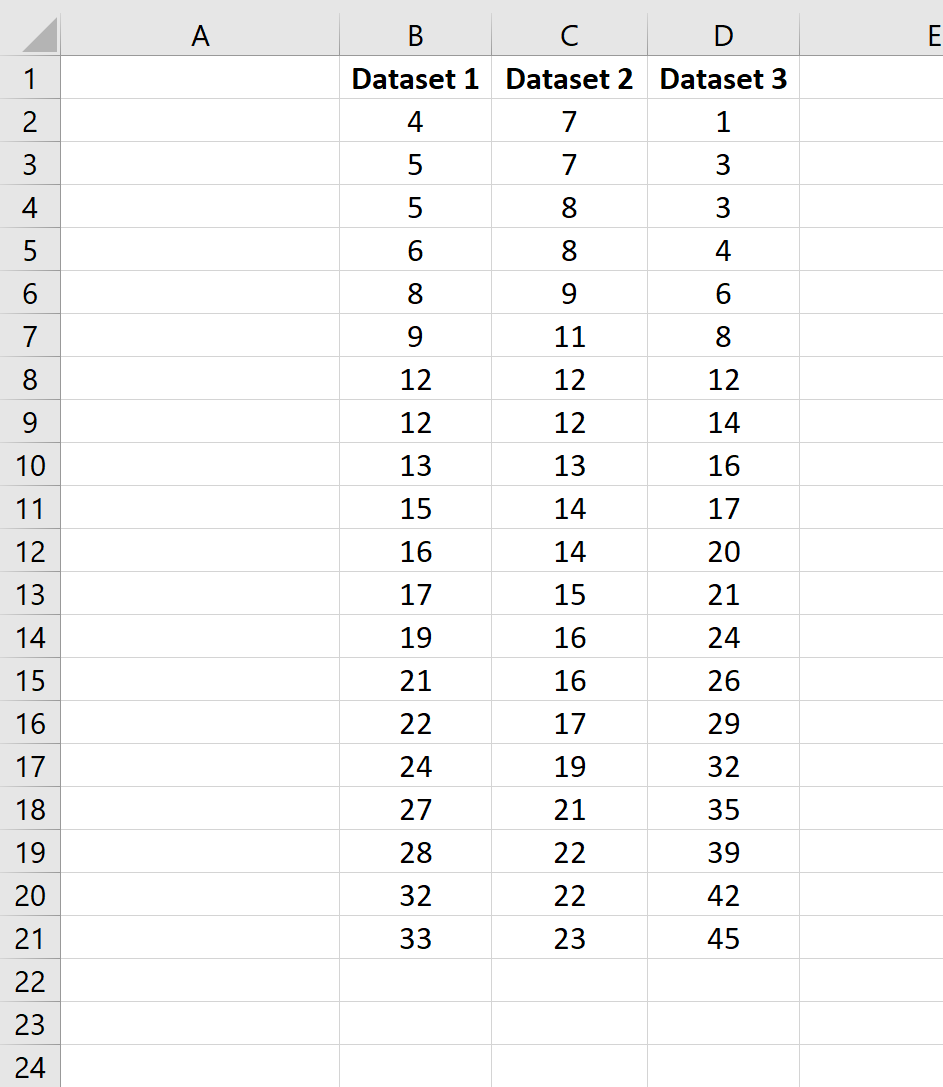
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
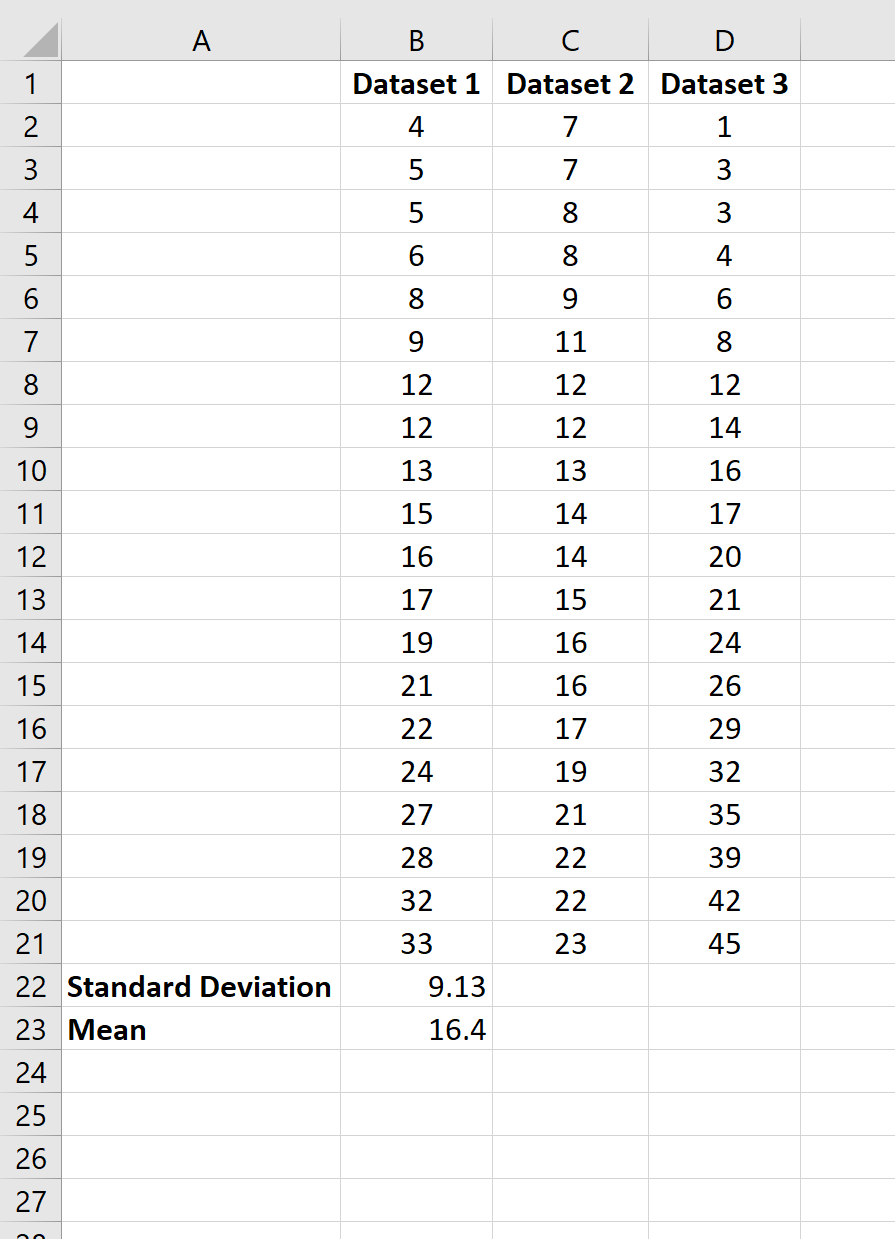
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
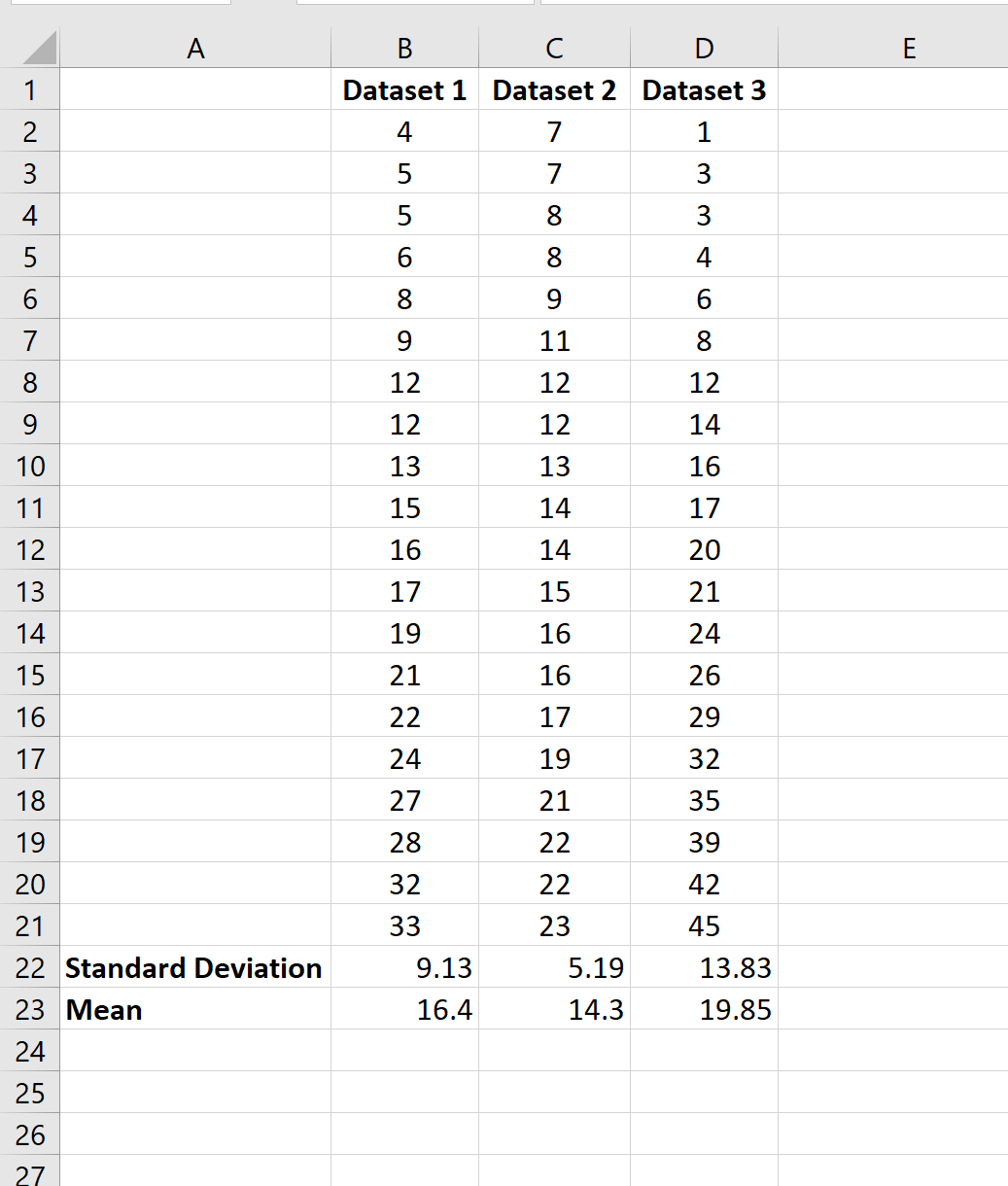
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Стандартное отклонение – одна из многих статистических данных, которые вы можете вычислить в Excel. Хотя процесс прост, вычисление стандартного отклонения в Excel может сбивать с толку новичков или людей, не знакомых с Microsoft Excel.
Тебе это тяжело? Без проблем. В этой статье мы покажем все способы расчета стандартного отклонения в Excel.
Что такое стандартное отклонение?
Стандартное отклонение показывает разницу между группой данных и их средним или средним значением. По сути, он возвращает значение, которое говорит вам, насколько ваши данные отклоняются от среднего значения.
Стандартное отклонение не работает с категориальными данными. Вы можете использовать его только для числовых данных.
Как и другие статистические данные, Excel предлагает различные способы расчета стандартного отклонения. Вы можете сделать это с помощью метода формулы или с помощью параметра «Вставить функцию» на ленте Excel. Мы рассмотрим каждый из доступных способов ниже.
Использование параметра «Вставить функцию» позволяет избежать необходимости изучать формулы Excel. Однако этот метод записывает фактическую формулу в выбранную ячейку результата и строку формул. Таким образом, это также может быть одним из способов быстро найти полезные формулы Excel .
Вот как рассчитать стандартное отклонение в Microsoft Excel с помощью метода вставки функции:
- Создайте новый столбец в своей электронной таблице, чтобы сохранить результат стандартного отклонения. Вы можете дать ему любое имя.
- Выберите любую ячейку в созданном вами столбце.
- Перейдите на ленту Excel и щелкните Формулы .
- Затем посмотрите на левый край ленты и нажмите « Вставить функцию» .
- В меню прокрутите параметры в окне « Выбор функции» и выберите « СТАНДОТКЛОН» , что означает стандартное отклонение.
- Щелкните ОК .
- Затем выделите столбец, для которого нужно рассчитать стандартное отклонение.
- Нажмите ОК, чтобы вычислить стандартное отклонение и вставить результат в первоначально выбранную ячейку.
Примечание. Хотя вам не нужно выполнять первые два шага для расчета стандартного отклонения, они помогают упорядочить результаты. Это означает, что вы можете выбрать любую ячейку в своей электронной таблице, чтобы сохранить результат стандартного отклонения, без необходимости создания нового столбца.
Как вставить результат стандартного отклонения на другой лист Excel
Вы также можете отделить стандартное отклонение от исходных данных, вставив его в другую электронную таблицу. Этот метод полезен, если вы хотите отделить статистические результаты от исходных данных. Вы также можете сделать это для другой базовой статистики в Excel .
Используя метод вставки функции выше:
- Создайте новый лист, щелкнув значок « Добавить» ( + ) в нижнем левом углу Excel.
- На новом листе выберите столбец для хранения результата стандартного отклонения и дайте ему имя.
- Затем щелкните ячейку в этом столбце.
- Находясь на новом листе, щелкните на ленте Формулы> Вставить функцию .
- Как и выше, просмотрите параметры в меню и выберите STDEV , затем нажмите OK .
- Вернитесь к листу с исходными данными и выделите столбец, для которого нужно рассчитать стандартное отклонение.
- Нажмите ОК, чтобы вставить результат на новый лист.
Как рассчитать стандартное отклонение в Excel с помощью параметра формулы
Использование формулы может пригодиться, когда вам нужно быстро выполнить задачу и сэкономить время в Microsoft Excel . Это будет проще, если вы хорошо разбираетесь в ярлыках и формулах Excel. Но даже если вы все еще учитесь, формулу стандартного отклонения довольно легко освоить.
Чтобы найти стандартное отклонение с помощью формулы Excel:
- Откройте электронную таблицу и создайте новый столбец для хранения результатов стандартного отклонения. Дайте столбцу имя.
- Предположим, что столбец с вашими данными – это столбец H , и предположим, что вы хотите рассчитать стандартное отклонение для строк с 1 по 14. Выберите ячейку в новом типе столбца: = STDEV (H1: H14) .
- Конечно, вам, вероятно, потребуется заменить H на соответствующий столбец для ваших данных и заменить 1 и 14 диапазоном строк, которые вы хотите охватить.
- Нажмите Return, чтобы завершить формулу, после чего Excel должен рассчитать стандартное отклонение за вас.
Объяснение стандартного отклонения совокупности и выборки
В зависимости от ваших конкретных потребностей вы можете вместо этого рассчитать генеральную совокупность или стандартное отклонение выборки.
Стандартное отклонение популяции оценивает расстояние каждого человека в популяции от среднего популяции. Вы используете его, когда имеете доступ к данным всего населения.
Чтобы рассчитать стандартное отклонение генеральной совокупности , используйте СТАНДОТКЛОН.P .
Стандартное отклонение выборки вычисляет стандартное отклонение от подмножества генеральной совокупности. Вы используете его, когда не хотите оценивать всю совокупность, а для статистики достаточно выборки.
Значение стандартного отклонения выборки обычно выше, чем стандартное отклонение генеральной совокупности.
Чтобы вычислить стандартное отклонение выборки в Excel, используйте STDEV.S вместо STDEV .
Какой метод стандартного отклонения лучше?
Хотя мы выделили несколько различных способов вычисления стандартного отклонения в Excel, вы все равно можете немного запутаться в том, какой из них следует использовать. Все методы, которые мы объяснили, полезны, и нет лучшего метода. Таким образом, тот, который вы решите использовать, зависит от вашего выбора и того, чего вы собираетесь достичь.
Однако метод формул наиболее полезен, если вы хотите ознакомиться с формулами и ярлыками Excel.
Помимо расчета стандартного отклонения, Excel также предлагает множество других статистических данных. Среднее значение, медиана, режим и другие средние значения доступны в Excel, и это еще не все.
Шаги
-

1
Запустите Microsoft Excel. Дважды щелкните по значку в виде белой буквы «X» на зеленом фоне. Как правило, он находится на рабочем столе или на панели задач. Откроется начальная страница Excel.
- Если у вас есть готовая таблица Excel с нужными данными, дважды щелкните по файлу, чтобы открыть его в Excel, а затем перейдите к шагу «Щелкните по пустой ячейке».
-

2
Нажмите Новая книга. Эта опция находится в верхней левой части начальной страницы Excel.
-

3
Введите данные. Выберите столбец, а затем введите нужные данные в ячейки этого столбца.
- Например, если вы выбрали столбец «A», введите числа в ячейки «A1», «A2», «A3» и так далее.
-

4
Щелкните по пустой ячейке. Это ячейка, в которой отобразится значение стандартного отклонения. Так вы выберете ячейку.
-

5
Введите формулу для вычисления стандартного отклонения. В пустой ячейке введите =СТАНДОТКЛОН.Г(), где «Г» — генеральная совокупность. Стандартное отклонение по генеральной совокупности учитывает все данные (N).[1]
- Чтобы найти стандартное отклонение по выборке, введите =СТАНДОТКЛОН.В(). В этом случае учитывается (N-1) данных.
-

6
Введите диапазон значений. Внутри круглых скобок введите букву и номер ячейки с первым числом, потом введите двоеточие (:), а затем введите букву и номер ячейки с посленим числом.
- Например, если вы ввели числа в столбце «A» в строках с 1 по 10, формула должна выглядеть так: =СТАНДОТКЛОН.Г(A1:A10).
- Чтобы посчитать стандартное отклонение нескольких чисел, которые, например, находятся в ячейках A1, B3 и C5, введите адреса ячеек через запятые (например, =СТАНДОТКЛОН.В(A1,B3,C5)).
-

7
Нажмите ↵ Enter. Формула будет выполнена, а в ячейке с формулой отобразится стандартное отклонение выбранных данных.
Реклама
Советы
- В большинстве случаев вычисляется стандартное отклонение по генеральной совокупности, чтобы учесть все данные.
Реклама
Предупреждения
- Старая формула =СТАНДОТКЛОН() не работает в версиях Excel старше 2007 года.
Реклама
Об этой статье
Эту страницу просматривали 116 291 раз.
