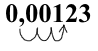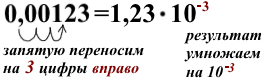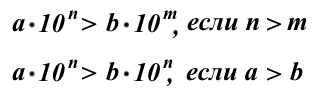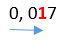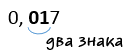Как найти стандартный вид числа - Сайт, где вы сможете решить свои вопросы

Стандартный вид числа

Определение

Стандартный вид числа — это его запись в виде произведения

где

Число n называется порядком числа, записанного в стандартном виде.

В стандартном виде можно записать любое положительное число.

Как правило, стандартный вид числа используют для записи больших и малых величин.

Примеры.

Записать число в стандартном виде и указать порядок числа:

1) 8 765 000;

2) 12 346 000 000;

3) 723,4;

4) 0,00123;

5) 0,000057;

6) 0,000729;

7) 5430·10⁵;

8) 0,0321·10⁸;

$[ 9)0,23 cdot 10^{ - 3} ; ]$

$[ 10)475 cdot 10^{ - 12} . ]$

Решение:

Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a<10), второй — степень десяти.

1) Число 8 765 000 больше 10. Запятой в числе не видим, значит, по умолчанию она находится в конце записи:

8 765 000= 8 765 000,

Если перенести запятую влево на 6 знаков, получим число, большее 1 и меньшее 10:

На 6 знаков влево запятую переносим при делении числа на миллион:

1 000 000 =10⁶, то есть данное число разделили на 10⁶. Чтобы число не изменилось, умножаем результат на 10⁶:

Получили число, записанное в стандартном виде. Его порядок n=6.

При решении примеров на приведение числа к стандартному виду удобнее деление числа на

заменить умножением на

$[10^{ - n} ,]$

то есть

$[8765000 = 8765000 cdot 10^{ - 6} cdot 10^6 = ]$

Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:

2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:

$[ 12346000000 = 1,2346 cdot 10^{10} . ]$

Это число записано в стандартном виде. Его порядок n=10.

3) 723,4

Чтобы первый множитель соответствовал условию 1≤a<10, нужно перенести запятую в записи числа на 2 цифры влево. Чтобы число не изменилось, умножим результат на 10²:

723,4=7,234·10².

Результат — число, записанное в стандартном виде. Его порядок n=2.

4) Чтобы первый множитель в стандартной записи числа удовлетворял условию 1≤a<10, запятую в 0,00123 нужно перенести на 3 цифры вправо

что соответствует умножению числа на 10³. Чтобы число не изменилось, результат умножаем на 10 в минус третьей степени:

$[0,00123 = 1,23 cdot 10^{ - 3} .]$

Порядок числа n= -3.

Таким образом, для приведения к стандартному виду числа, меньшего единицы, запятую в его записи переносим на n цифр вправо и результат умножаем на 10 в степени -n:

$[ 5)0,000057 = 5,7 cdot 10^{ - 5} ]$

Переносим запятую в записи числа на 5 цифр вправо (что соответствует умножению числа на 10⁵). Результат умножаем на 10 в минус пятой степени. Порядок числа n= -5.

$[ 6)0,000729 = 7,29 cdot 10^{ - 4} ]$

Порядок числа n= -4.

Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.

Далее выполняем умножение степеней с одинаковыми основаниями.

Порядок числа n=6.

$[ 8)0,0321 cdot 10^8 = 3,21 cdot 10^{ - 2} cdot 10^8 = ]$

Порядок числа n=6.

$[ 9)0,23 cdot 10^{ - 3} = 2,3 cdot 10^{ - 1} cdot 10^{ - 3} = ]$

$[ = 2,3 cdot 10^{ - 4} ]$

Порядок числа n= -4.

$[ 10)475 cdot 10^{ - 12} = 4,75 cdot 10^2 cdot 10^{ - 12} = ]$

$[ = 4,75 cdot 10^{ - 10} ]$

Порядок числа n= -10.

Сравнение чисел, записанные в стандартном виде

Сравниваем порядок чисел. Число с большим порядком больше числа с меньшим порядком.
Если числа имеют одинаковые порядки, сравнивают первые множители произведения.

Примеры

так как порядок первого числа больше порядка второго числа (8>7);

$[ 2)7,5 cdot 10^{ - 8} < 1,6 cdot 10^{ - 7} ]$

поскольку порядок первого числа меньше порядка второго числа (-8<-7);

так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).

Источник

Стандартный вид положительного числа (a) — запись этого числа в виде a0⋅10m, причём 1≤a0<10, a число (m) — целое. Число (m) является порядком числа (a).

Итак, для того чтобы любое число было записано в стандартном виде, нужно, чтобы запятая стояла в числе a0 сразу после первой значащей цифры.

Обрати внимание!

Значащими цифрами числа называют его первую слева ненулевую цифру и все последующие за ней цифры.

Пример:

запиши число в стандартном виде и укажи порядок числа:

1) порядок числа 274,35=2,7435⋅102 равен (2);

2) порядок числа 0,005434=5,434⋅10−3 равен (-3);

3) порядок числа 2,654 равен (0).

По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра. Все остальные цифры должны стоять после (справа от) запятой.

Переход к стандартному виду числа используют для вычисления или для работы с очень большими или с очень маленькими положительными числами.

Источник

Наверняка, в физике, биологии, химии или
географии вы сталкивались, как с очень большими, так и очень малыми
положительными числами.

Например

Скажите с такими числами удобно выполнять
математические расчёты? Конечно же, нет. В обычном десятичном виде большие и
малые числа неудобно читать и записывать, неудобно выполнять над ними
какие-либо действия. В таком случае полезным оказывается представление числа в
виде

Например:

Тогда

Говорят, что мы записали числа в стандартном
виде. В таком виде можно представить любое положительное число.

Определение:

Стандартным видом числа называют его
запись в виде: , где и
–
целое число.

Число называется
порядком числа .

Например

Если порядок числа равен , то это означает,
что .

Большой положительный порядок
показывает, что число очень велико.

Большой по модулю отрицательный порядок
показывает, что число очень мало.

, где и – целое число

По определению стандартного вида числа
следует, что в стандартном виде в целой части числа (до запятой) может
содержаться только одна цифра.

Все остальные цифры должны стоять после
(справа) от запятой.

Порядок числа даёт представление о том,
насколько велико или мало это число.

В стандартном виде можно записать не только
большое или малое, но и любое число.

Для того чтобы привести число к стандартному виду, надо:

1. Перенести в нём запятую так, чтобы она была сразу
после первой значащей цифры.

2.
полученное число умножить на , где подбирается так, чтобы произведение было равно
данному числу.

Значащей цифрой числа
называют его первую (слева направо) отличную от нуля цифру, а также все
последующие за ней цифры.

Пример: представим в
стандартном виде число.

Решение:

Задание: запишите число в
стандартном виде.

Решение:

Задание: запишите в
стандартном виде число, равное значению произведения х и у.

Решение:

Итоги:

Стандартным видом числа называют его запись
в виде: , где и – целое число.

Число
называется порядком числа .

Для
того, чтобы привести число к стандартному виду, надо перенести в нём
запятую так, чтобы она была сразу после первой значащей цифры, и полученное
число умножить на , где подбирается так, чтобы произведение было равно
данному числу.

Источник

В задачах по физике часто приходится работать с очень большими и очень малыми величинами.

Как вести вычисления в атомной физике? Или записать радиус электрона?
Если потребуется сравнить массу электрона и массу планеты Земля,
как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?

Физики и математики, столкнувшись с такими задачами, поняли,
что для решения подобных задач требуется привести числа к единому стандартному виду.
Так появилось понятие стандартный вид числа.

Прежде чем переходить к объяснению, как записать число в стандартном виде,
нужно вспомнить определение степени.
Особенно хорошо нужно помнить, чему равняется число
«10» в различных степенях.

10⁻² =
= = 0,01

(более подробно об отрицательной степени можно прочитать в уроке 9 класса
«Отрицательная степень»)
10⁻¹ =
=
= 0,1
10⁰ = 1
10¹ = 10
10² = 100
10³ = 1000
…

Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы
просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..

5 · 10 = 50
27 · 100 = 2 700
18 · 1000 = 18 000

Теперь запишем тоже самое, используя определение
степени.

5 · 10 = 5 · 10¹ = 50
27 · 100 = 27 · 10² = 2 700
18 · 1000 = 18 · 10³ = 18 000

При делении целого числа на 10, 100, 1000 и т.д. мы
убирали нули.

13 000 : 100 = = 130
50 : 10 = = 5

Для десятичных дробей действует схожее
правило умножения на 10, 100, 1000.
При умножении десятичной дроби на 10, 100, 1000 и т.д.
мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д…

5,7 · 100 = 570
7,013 · 10 = 70,13
68,3 · 1000 = 68 300

С помощью степени можно записать вычисления выше следующим образом:

5,7 · 100 = 5,7 · 10² = 570
7,013 · 10 = 7,013 · 10¹ = 70,13
68,3 · 1000 = 68,3 · 10³ = 68 300

При делении на 10, 100, 1000 и т.д. перемещаем запятую влево.

6,7 : 10 = = 0,67
0,15 : 100 = = 0,0015

С помощью определения
отрицательной степени
можно записать вычисления выше следующим образом:

6,7 : 10 = = 6,7 · 10⁻¹ = 0,67
0,15 : 100 = = 0,15 · 10⁻² = 0,0015

Стандартный вид числа

Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.

Запомните!

Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:

a · 10ⁿ,
где 1 ≤ a < 10
и n — натуральное число.

Такая запись называется — стандартный вид числа.
При этом число
«n»
называют порядком числа «a».

Из определения выше важно понять, что степень, в которой стоит «10», в стандартном
виде числа называется порядком.

Теперь к примеру. Пусть нам дано число «5 600» и требуется записать его в стандартном виде.

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от
«1»
до «9».

В числе «5 600» первая цифра справа — «5».
Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.

Значит, чтобы из «5,600»
получить «5600» нам нужно умножить
«5,600» на «1000». Запишем полученное преобразование.

5 600 = 5,600 · 1000

Теперь запишем «1000» с использованием степени.

5 600 = 5,600 · 1000 = 5,600 · 10³

Завершающим штрихом будет
отбрасывание незначащих нулей в десятичной дроби.

5 600 = 5,600 · 1000 = 5,600 · 10³

=
5,6 · 10³

Таким образом «5 600» в стандартном виде будет выглядеть следующим образом:

5 600 = 5,6 · 10³

Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно.
Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.

5,6 · 10³ = 5 600

Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь
«0,017».

Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра
от «1» до «9».

В десятичной дроби «0,017» вначале идет
«0». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от
«0».

Это цифра «1».
Посчитаем сколько знаков (цифр) стояло от запятой до цифры «1», включая саму цифру «1».

Получается два знака.
Начнем записывать «0,017» в стандартном виде.
Перенесем запятую и поставим ее справа от «1».

0,017 = 1,7 · 10…

Ответим себе на вопрос: “На что нужно умножить или разделить «1,7», чтобы получить изначальное число
«0,017» ?”.
Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится
Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится
влево.

Выходит, чтобы из «1,7» сделать 0,017»,
нужно «1,7 разделить на «100» (чтобы перенести
запятую на два знака влево).

0,017 = 1,7 : 100

Запишем это деление на «100», используя
обыкновенную дробь.

0,017 = 1,7 : 100 = 1,7 ·

С помощью отрицательной степени запишем окончательный вид числа
«0,017» в стандартном виде.

0,017 = 1,7 : 100 = 1,7 ·

=

1,7 · 10⁻²

Примеры решения задач
на запись числа в стандартном виде

Разбор примера

Определить порядок числа, выражающего значение физической константы:

1) масса покоя электрона
m_e = 9,1093897 · 10⁻³¹

Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень,
в которой стоит «10».
В данном примере «10» стоит в
степени
«−31».
Значит, порядком массы покоя электрона является «−31».

Разбор примера

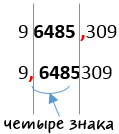
Записать в стандартном виде и определить порядок числа k, выражающего физического константу:

2) постоянная Фарадея
F = 96485,309 Кл/моль;

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от
«1» до «9».

Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра
«9».

96485,309 = 9,6485309 · 10…

Зададим себе вопрос: «На что нужно умножить
«9,6485309», чтобы получить
«96485,309» ?»
Посчитаем количество знаков (цифр), на которое требуется перенести запятую
в «96485,309»,
чтобы получить «96485309».

Получается «4» знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим
образом:

96485,309 = 9,6485309 · 10⁴

Порядком числа «9,6485309 · 10⁴» является степень, в которой стоит
«10». Следовательно, порядок
«k = 4».

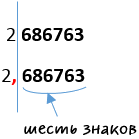
3) Постоянная Лошмидта
n₀ = 2686763 · 10 ²⁶

Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:

2686763 · 10 ²⁶ =
2,686763 · 10 ²⁶ · 10…

Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую,
чтобы из «2,686763» получить
«2686763».

Значит, чтобы получить из «2,686763» нужно изначальное число
«2686763» умножить на «10⁶».

2686763 =
2,686763 · 10 ²⁶ · 10⁶

Завершим решение и запишем окончательный ответ, используя свойство
«Произведение степеней».

2686763 = 2,686763 · 10 ²⁶ · 10⁶ =
2,686763 · 10 ^{26 + 6} = 2,686763 · 10 ³²

Другие примеры записи чисел в стандартном виде

0,52 = 5,2 · 10 ⁻¹
401 = 4,01 · 10 ²
60,756 = 6,0756 · 10¹
0,00123 = 1,23 · 10⁻³

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

9 сентября 2015 в 17:32

Ирина Колесник
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ирина Колесник
Профиль
Благодарили: 0

Сообщений: 1

Нужно представить число в стандартном виде, а для меня это в новинку, не могу решить, помогите пожалуйста, зарание спасибо0,0000000058=
0,0245=
0,000000985
0,002=
0,00003598=
2500000000=
36800000000000000=
536700000=
520000=

0
Спасибо thanks
Ответить

5 сентября 2016 в 9:20
Ответ для Ирина Колесник

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

В данной теме достаточно подробно освещён данный вопрос: math-prosto.ru/?page=pages/standard_form_number/standard_form_number.php

0,0000000058=5,8 · 10^-9
0,0245=2,45 · 10^-2
0,000000985= 9,85 · 10^-7
0,002=2 · 10^-3
0,00003598=3,598 · 10^-5
2500000000=2,5 · 10⁹
36800000000000000=3,68 · 10¹⁶
536700000=5,367 · 10⁸
520000= 5,2 · 10⁵

0
Спасибо thanks
Ответить

3 июня 2015 в 19:18

Евгения Данилина
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Евгения Данилина
Профиль
Благодарили: 0

Сообщений: 4

Выразите в сантиметрах 3,754

0
Спасибо thanks
Ответить

3 июня 2015 в 19:46
Ответ для Евгения Данилина

Кирилл Гуменюк
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Кирилл Гуменюк
Профиль
Благодарили: 0

Сообщений: 2

3,754 в чём?

0
Спасибо thanks
Ответить

6 июня 2015 в 12:01
Ответ для Евгения Данилина

Евгения Данилина
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Евгения Данилина
Профиль
Благодарили: 0

Сообщений: 4

там не написано в чём

0
Спасибо thanks
Ответить

3 июня 2015 в 19:08

Кирилл Гуменюк
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Кирилл Гуменюк
Профиль
Благодарили: 0

Сообщений: 2

порядок числа а равен -3.узнайте порядок числа 0,01а

0
Спасибо thanks
Ответить

30 мая 2016 в 11:57
Ответ для Кирилл Гуменюк

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Порядок числа a равен -3. Значит порядок числа а 10^-3. 0,01 = 10^-2. Значит порядок числа 0,01а равен 10^-3 · 10^-2=10^-5 и равен -5.

Ответ: порядок числа 0,01а равен -5.

0
Спасибо thanks
Ответить

3 февраля 2017 в 21:20
Ответ для Кирилл Гуменюк

Антонина Никулина
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Антонина Никулина
Профиль
Благодарили: 0

Сообщений: 1

0,01*-3=-0,03

0
Спасибо thanks
Ответить

Источник

Стандартный вид числа

Стандартный вид числа — это запись числа в виде произведения:

x · 10ⁿ,

где 1 ⩽ x < 10, n — целое число.

С помощью целых показателей степени числа 10 можно записывать очень большие и очень маленькие числа в стандартном виде, то есть громоздкие записи заменять краткими. Рассмотрим несколько примеров записи чисел в стандартном виде:

56000 = 5,6 · 10⁴;

314,7 = 3,147 · 10²;

5400000000 = 5,4 · 10⁹;

0,00038 = 3,8 · 10^-4.

Обратите внимание, что в стандартном виде число, которое умножается на 10 в какой-либо степени, всегда должно быть больше или равно единице и меньше десяти. Следовательно, если мы перепишем наши примеры так:

56000 = 56 · 10³;

314,7 = 0,3147 · 10³;

5400000000 = 540 · 10⁷;

0,00038 = 38 · 10^-5;

то записи чисел хоть и будут выглядеть похожими на стандартный вид, но к числам в стандартном виде они не будут иметь никакого отношения.

Любое однозначное число в стандартном виде представляет собой произведение самого себя на 10 в нулевой степени:

1 = 1 · 10⁰	6 = 6 · 10⁰
2 = 2 · 10⁰	7 = 7 · 10⁰
3 = 3 · 10⁰	8 = 8 · 10⁰
4 = 4 · 10⁰	9 = 9 · 10⁰
5 = 5 · 10⁰

Число 10 в стандартном виде равно произведению единицы на 10 в первой степени:

10 = 1 · 10¹.

Примечание: число 0 нельзя представить в стандартном виде.

Примеры. Запишите число в стандартном виде:

1) 2400;	5) 38;
2) 8600;	6) 387;
3) 0,00019;	7) 1280000;
4) 37000000;	8) 2370000.

Решение:

1) 2400 = 2,4 · 10³;

2) 8600 = 8,6 · 10³;

3) 0,00019 = 1,9 · 10^-4;

4) 37000000 = 3,7 · 10⁷;

5) 38 = 3,8 · 10¹;

6) 387 = 3,87 · 10²;

7) 1280000 = 1,28 · 10⁶;

8) 2370000 = 2,37 · 10⁶.

Источник

Стандартный вид числа

Примеры решения задач на запись числа в стандартном виде

Разбор примера

Разбор примера

Другие примеры записи чисел в стандартном виде

Ваши комментарии

Стандартный вид числа

Вам также может понравиться

Шрифт arial cyr как найти

Как найти изменение энтропии тела

Зубы как исправит привкус

Добавить комментарий Отменить ответ

Примеры решения задач
на запись числа в стандартном виде