Мастер
(1415),
закрыт
11 лет назад
Алекс- 89
Гений
(85771)
11 лет назад
В этом числе старшим разрядом является 8. Старший разряд — это просто-напросто первая цифра числа. При условии, что эта цифра не равна нулю.
ElizabethМастер (1415)
11 лет назад
Дело в том,что на уроке математики в числе 2,35 определили старший разряд ноль. В числе 0,1253 старш разряд -1. Вот я и не могу понять в чем суть
Анна ЯщенкоЗнаток (281)
6 лет назад
боже, это же неправильно.
старший разряд в числе 8,6 равен 0,потому что разряд цифры числа это по сути ее степень: 8,6=8*10^0+6*10^-1
экономика Институт экономики и управления
Профи
(582)
6 лет назад
Номер позиции символа (цифры) в числе называется разрядом. Крайний левый разряд числа называется старшим разрядом, а крайний правый – младшим разрядом этого числа. Количество символов в числе определяют разрядность числа. Нумерация разрядов целой части производится справа налево от десятичной точки, от 0 доn. Нумерация разрядов дробной части производится слева направо от десятичной точки, от -1 до –m. Т. Е. старший разряд числа будет равен 0
|
Математика. Что такое старший, средний, младший разряд числа (приведите примеры)?
Младший разряд числа всегда показывает простые числа (от 0 до 9). Старший разряд показывает числа, которые умножены на 10^(n-1), где n – количество знаков числа. Если число двухзначное, например 36, то младший разряд – это число 6, а старший разряд – это число 3, которое для составления этого числа было умножено на число 10 (десятки). Если число трёхзначное, например, 174, то младший разряд – это число 4, средний разряд – это число 7, умноженное на 10 (десятки), старший разряд – это число 1, умноженное на 100 (сотни). В двоичной системе счисления есть цифры 0 и 1, и там разряды накапливаются по степеням числа 2. Например, двоичное число 10 соответствует реальному числу 2, двоичное число 111 соответствует реальному числу 7. Вывод: младший разряд ставится справа и показывает простые числа, старший разряд ставится слева и он показывает максимальную разрядность числа; чем больше знаков, тем больше будет разрядов между старшим и младшим разрядам числа; средний разряд есть в трёхзначных и многозначных числах. автор вопроса выбрал этот ответ лучшим
Марина Вологда более года назад В математике числа подразделяются на классы, в которых выделяются разряды. Давайте вспомним, что такое разряд в математике. Допустим, у нас дано такое число: 1234. Распишем это число: 1 тысяча, 2 сотни, 3 десятка, 4 единицы. Если говорить о разрядах, тогда звучит так: 1 – разряд тысячных, 2 – разряд сотен, 3 – разряд десятков и 4 – разряд единиц. Самый низший разряд всегда является разряд единиц, в нашем случае это 4. Самый высший разряд, это то число, которое стоит первым, у нас это разряд тысячных, т.е. 1. Ну а средний разряд – это то, что стоит между левым и правым числом, у нас это 2 сотни и 3 десятка. Ну и вот разряды, которые стоит помнить:
Алиса в Стране более года назад Рассмотрим на примерах. Возьмем число 78. Если в числе две цифры, значит в нем есть десятки и единицы, в таком случае десятки будут старшим разрядом числа, единицы – младшим, допустим в числе 78, 7 – старший разряд числа, обозначает количество десятков, 8 – младший разряд числа – показывает, сколько в числе единиц. Число единиц это всегда младший разряд числа, это самая правая цифра в числе. Старший разряд – самая левая цифра. Возьмем трехзначное теперь число, в числе 357 старший разряд – 3, младший – 7, а 5 – средний разряд числа. Иначе можно сказать, что разрядом определяется положение цифры в записи числа.
Бархатные лапки более года назад Ну на самом деле разобраться в этом можно, не так все страшно, как кажется на первый взгляд. Если речь у нас идет о трехзначном числе, то тогда: Младший разряд у нас – разряд единиц; Старший разряд соответственно разряд сотен; А вот средний разряд, как несложно догадаться будет разряд десятков. Возьмем такое число, как 742 и рассмотрим его. Итак у нас 7 является старшим разрядом, число 4 – это средний разряд, ну и 2 – это младший разряд. Но если число больше, чем трехзначное, то тогда, первая цифра будет старшим разрядом, последняя циферка является младшим разрядом, ну а циферки, которые посередине – средний разряд.
Hamster1337 2 года назад Разряд числа представляет собой структурный элемент представления числа в позиционной системе счисления. Например число 28 имеет 2 разряда: младший число “8”, а старший число 2 (средний разряд в данном числе отсутствует). Число 829 имеет 3 разряда: младший “9”, средний “2”, старший “8”.
Real M более года назад Разрядом называется место, где находится цифра. Читаются разряды справа налево. Получается, что после последняя цифра-это младший разряд, а первая цифра является старшим разрядом. Например в числе 736, число “6”-это младший разряд, “7”-старший разряд. Причём “6”-то разряд единиц. “3”-разряд десятков. “7”-разряд сотен. Если разложить это число, то получим: 1+1+1+1+1+1=6-шесть единиц 10+10+10=30-три десятка 100+100+100+100+100+100+100=700-семь сотен Таким образом, если сложить 6+30+700=736 Если число четырёхзначное, то к ним добавляем разряд тысяч, пятизначное десятков тысяч, шестизначное, разряд сотен тысяч, а семизначное разряд миллионов.
KritikSPb 4 года назад Младший разряд числа – это самая последняя цифра в числе. Например, в числе 1584 младшим разрядом будет цифра 4. Старший разряд – это самая первая цифра в числе. Пример: берем число 296, тут старшим разрядом является цифра 2. В двузначных числах от 10 до 99 только старший и младший разряды, а вот во всех числах больше 100 уже есть и цифры среднего разряда – это всё, что находится посередине. В числе 158 цифра среднего разряда 5. В числе 2584236 таких цифр пять, это 5,8,4,2 и 3. Арнольд Семенович 2 года назад Если взять все числа от 0 и заканчивая их 9, то получится такой себе ряд, который и будет младшим разрядом. Старший разряд – это не то иное, как умножение младшего на 10 в степени, равной количеству цифр в числе минус 1. Но, в числах из 3 и более чисел уже появляется средний разряд, который будет посредине между младшим/старшим. Что получается – 254 тут так – старший (2), средний (5) и младший (4). Лара Изюминка 3 года назад Все достаточно просто, если речь идёт о трехзначном числе, то младший разряд это разряд единиц, средний разряд это разряд десятков, старший разряд это разряд сотен. Так если число 425, то 4 старший разряд, 2 средний разряд, 5 младший разряд. Если числа больше чем трехзначные то младший разряд – всегда последняя цифра, это всегда разряд единиц, старший разряд – это первая цифра. Vodila более года назад Скорее всего речь идет о трехзначном числе, раз в вопросе указано три разряда. Итак, старший разряд тогда получается разряд сотен, средний разряд десятков, а младший – это разряд единиц. Кстати в любом числе младший разряд всегда разряд единиц. Знаете ответ? |
В математике разряды чисел — это позиции цифр в числе (место, где располагается цифра). Их нужно читать справа налево.
Рассмотрим число 345, которое состоит из трех цифр:
➤ первая позиция — цифра 5 — разряд единиц
➤ вторая позиция — цифра 4 —разряд десятков
➤ третья позиция — цифра 3 —разряд сотен
Разряды также сообщают нам информацию о количестве единиц, десятков и сотен.
➤ первая позиция — цифра 5 — разряд единиц содержит 5 единиц (1+1+1+1+1)
➤ вторая позиция — цифра 4 —разряд десятков содержит четыре десятка (10+10+10+10)
➤ третья позиция — цифра 3 —разряд сотен содержит три сотни (100+100+100)
Если сложить число единиц, число десятков и число сотен, то получим наше изначальное число 345:
(1+1+1+1+1)+(10+10+10+10)+(100+100+100)
Слова единицы, десятки, сотни, заменяют собой множители 1, 10 и 100.
Например, рассмотрим наше число 345:
➤ в разряде единиц — множитель 1 содержится в разряде единиц 5 раз: 1 × 5 = 5
➤ в разряде десятков — множитель 10 содержится в разряде десятков 4 раза: 10 × 4 = 40
➤ в разряде сотен — множитель 100 содержится в разряде сотен 3 раза: 100 × 3 = 300
Если сложить полученные результаты 5 + 40 + 300, то получим число 345.
Другие группировки
➤ То же самое будет происходить если мы скажем, что число 345 содержит 34 десятка и 3 единицы. Другими словами,
— десятки будут сгруппированы 34 раза: 10 × 34 = 340
— единицы будут сгруппированы 5 раз: 1 × 5 = 5
Если сложить полученные результаты 340 и 5, снова получим число 345.
➤ Также возможно группировка, при которой не будет распределения на десятки и сотни. В таком случае число 345 будет читаться как «триста сорок пять единиц»: 1 × 345 = 345.
Старшие разряды
Далее рассмотрим более старшие разряды: тысяч, десятков тысяч, сотен тысяч, миллионов и т.д.
Рассмотрим число: 1 234 567
разряд единиц — 7 единицы,
разряд десятков — 6 десятков,
разряд сотен — 5 сотен,
разряд тысяч — 4 тысячи,
разряд десятков тысяч — 3 десятка тысяч,
разряд сотен тысяч — 2 сотни тысяч,
разряд миллионов — 1 миллион.
Применение разрядов
Применение разрядов при решение примеров облегчают некоторые вычисления. Например, когда нужно сложить два трехзначных числа, то можно сложить все разряды по отдельности: единицы, десятки и сотни. Начинать нужно с разряда единиц и т.д.
Рассмотрим пример: 123 + 456 =
В первую очередь после знака равно (=) мысленно поставим три точки. Вместо этих точек будет располагаться новое число (наш ответ): 123 + 456 = . . .
Начинаем складывать:
1) из разряда единиц берем числа 3 и 6, получаем 9 ➜ 123 + 456 = . . 9
2) из разряда десятков берем числа 2 и 5, получаем 7 ➜ 123 + 456 = . 7 9
3) из разряда сотен берем числа 1 и 4, получаем 5 ➜ 123 + 456 = 5 7 9
Таким образом, если к числу 123 прибавить 456 , получается 579.
Этот принцип действует, если решать примеры в столбик:
? Важно! Каждый разряд записывается друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями и т.д. При неправильном размещении разрядов пример будет решен не правильно!
? Чтобы потренироваться решать примеры в столбик на сложение, можно скачать программу «Сложение и вычитание в столбик«.
Переполнение разряда
Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения может произойти переполнение разряда.
Рассмотрим пример: 56+89.
При сложении единиц этих чисел получаем 15 (6+9), а при сложении десятков получаем 13 (5+8).
1) При сложении 9 и 6 единиц у нас получилось 15 единиц — это 1 десяток и 5 единиц.
Поэтому в разряд десятков записываем 5, а 1 десяток мы будем прибавлять к десяткам при их сложении.
2) При сложении десятков получаем 13 (5+8) — это 1 сотня и 3 десятка.
Поэтому в разряд десятков мы запишем 4 (3 десятка + 1 десяток, полученный при сложении единиц). Так как в примере разряд сотней не складывается, то мы просто впереди приписываем единицу.
| 1 5 6 + 8 9 = . . ➜ 5 6 + 8 9 = . 5 ➜ 5 6 + 8 9 = 1 4 5 |
Этот принцип действует также при решении примеров в столбик:
|
+ |
1 |
|
1 1 |
|
| 1 4 5 | 6 2 7 |
Примеры на вычитание
Теперь рассмотрим примеры на вычитание. Вычитать также нужно по разрядам.
Пример: 68–45.
Начинаем с разряда единиц. При вычитании единиц этих чисел получаем 3 (8-5).
Затем вычитаем десятки. При вычитании десятков получаем 2(6-4).
6 8 – 4 5 = . . ➜ 6 8 – 4 5 = . 3 ➜ 6 8 – 4 5 = 2 3
Пример: 42-15.
1) В разряде единиц числа 42 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц нельзя вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.
Чтобы выполнить вычитание, две единицы должны взять несколько единиц у соседней группы (разряда десятков) ➜ Поэтому берем один десяток.
Получаем, что мы число 42 разделили на 3 десятка и 12 единиц. Из 12 вычитаем 5 и получаем 7. Записываем цифру 7 в разряде единиц нового числа.
2) Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не четыре, а три десятка. Поэтому вычитаем из 3 десятков один десяток. Останется 2 десятка. Записываем цифру 2 в разряде десятков нового числа.
Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.
| • • 4 2 – 1 5 = 4 2 – 1 5 = . 7 ➜ 4 2 – 1 5 = 2 7 |
Этот принцип действует также при решении примеров в столбик:
|
– |
• |
|
• • |
|
| 2 7 | 2 4 4 |
Во втором примере:
1) Вычитаем единицы. разряде единиц числа 823 содержится 3 единицы, а в разряде единиц числа 579 — 9 единиц. От 3 единиц не вычесть 9 единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток. Взятый один десяток и три единицы вместе образуют 13 единиц. От 13 единиц вычитаем 9 единиц, получится 4 единицы. Записываем цифру 4 в разряде единиц нового числа.
2) Вычитаем десятки. Раньше разряд десятков числа 823 содержал 2десятка, но мы взяли с него один десяток, и теперь в разряде десятков содержатся 1 десяток. Из 1 десятка нужно вычесть 7 десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню. Взятая 1 сотня и 1 десяток вместе образуют 11 десятков. От 11 десятков вычитаем 7 десятков, получаем 4 десятка. Записываем цифру 4 в разряде десятков нового числа.
3) Вычитаем сотни. Раньше разряд сотен числа 823 содержал 8 сотен, но мы взяли с него 1сотню, и теперь в разряде сотен содержатся 7 сотен. Из 7 сотен можно вычесть 5 сотен, получается 2 сотни. Записываем цифру 2 в разряде сотен нового числа.
? Чтобы потренироваться решать примеры в столбик на вычитание, можно скачать программу «Сложение и вычитание в столбик«.
Вычитание из круглых чисел
Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда.
Выполнять вычитание таким традиционным методом сложно, поэтому можно воспользоваться нестандартным способом. Для этого уменьшить вычитаемое число на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу.
Пример: 1000–123
1) уменьшим уменьшаемое на 1: 1000–1=999
2) из числа 999 вычтем 123: 999-123=876
3) к этому ответу прибавляем 1: 876+1=877.
Получили: 1000+123=877.
Разряды и классы чисел
- Классы чисел
- Разряды чисел
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
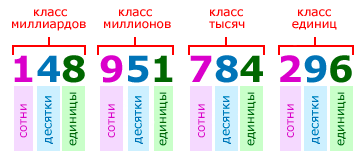
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
148 951 784 296
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц
.
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Разряд числа — это позиция (место) цифры в записи числа.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
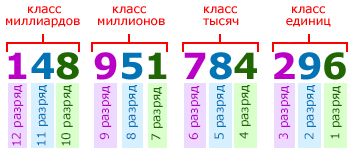
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
- Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
- Сотни — единицами третьего разряда и пишутся на третьем месте справа.
- Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
- Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Решение:
1) 37 565;
2) 450 009;
3) 8 050.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
и так далее.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра 0 в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
20 507 — двадцать тысяч пятьсот семь.
В данной публикации мы рассмотрим, что такое разряды чисел, и приведем примеры для лучшего понимания теоретического материала.
- Определение разряда
-
Примеры
Определение разряда
Как мы знаем, все натуральные числа состоят из цифр, которых всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Разряд – это место/позиция, которое цифра занимает в числе.
Позиция считается с конца числа к его началу. И в зависимости от занимаемого места, цифра может иметь разное значение.
Разряды располагаются в следующем порядке (по возрастанию: от младшего к старшему, т.е. справа налево):
- единицы;
- дестяки;
- сотни;
- тысячи и т.д.
Примеры
В качестве примера подробно разберем число 5672 (читается как “пять тысяч шестьсот семьдесят два”), а точнее разложим его на разряды.

- цифра 2 на последнем месте означает две единицы.
- 7 – это семь десятков;
- 6 – шесть сотен.
- 5 – пять тысяч.
Т.е. число 5672 можно разложить по разрядам следующим образом:
5 ⋅ 1000 + 6 ⋅ 100 + 7 ⋅ 10 + 2 = 5762.
Примечания:
- Есть числа, которые не содержат какой-то разряд, о чем свидетельствует цифра ноль на его месте. Например, так выглядит раскладка на разряды числа 10450:
10 ⋅ 10000 + 0 ⋅ 1000 + 4 ⋅ 100 + 5 ⋅ 10 + 0 = 10450. - Десять единиц любого разряда равны одной единице следующего, более старшего разряда. Например:
- 10 единиц = 1 десяток;
- 10 десятков = 10 сотня;
- 10 сотен = 1 тысяча и т.д.
- С учетом пункта выше получается, что значение цифры в каждом следующем разряде (более старшем) увеличивается в 10 раз, т.е. одна единица в 10 раз меньше одного десятка, один десяток в 10 раз меньше одной сотни и т.д.



