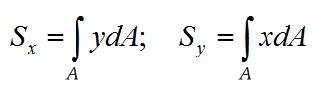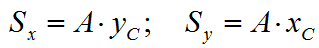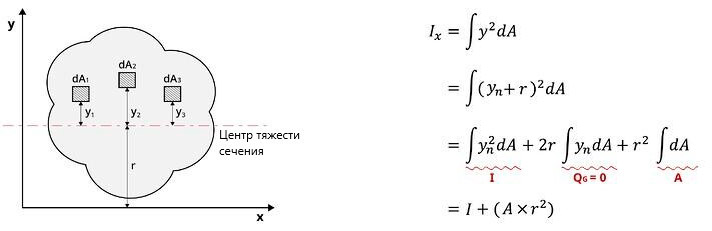6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ
Статический момент площади – распространенная на всю площадь сумма произведений элементарных площадок dA на расстояние от них до этой оси Это понятие аналогично моменту силы относительно оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус. Ось центральная – ось, относительно которой статический момент площади равен нулю. Центр тяжести сечения – точка пересечения центральных осей. Если фигура имеет ось симметрии, то эта ось является центральной. Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это следует из свойства определенного интеграла, который можно вычислять по частям – свойство аддитивности (от англ. add – прибавлять, присоединять, складывать). При известных статических Рис. 6.2. Связь знака статического момента площади с его положением в координатной системе моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры: Пример 6.1. Определить положение центральных осей, параллельных основанию и высоте фигуры. Решение Разбиваем сложную фигуру на две простые, в конкретном примере – на два прямоугольника. Их центры тяжести расположены посредине высоты и посредине ширины. Координаты центров тяжести и площади простых фигур Статические моменты площадей простых фигур Координаты центра тяжести составной фигуры Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте. Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.
Формулы для расчета геометрической характеристики статического момента сечений, плоских фигур и площади:
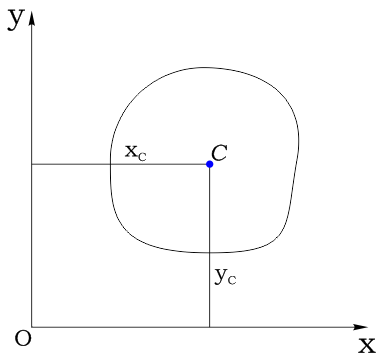
Рассмотрим сечение (плоскую фигуру) произвольной формы площадью A:
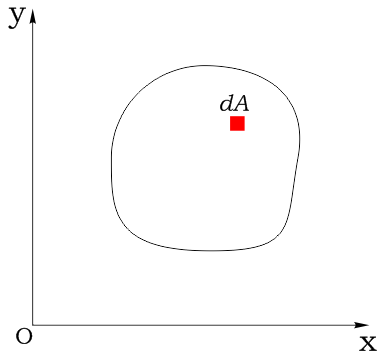
Выделим в нем элементарную площадку dA и зададим систему координат:
Другие видео
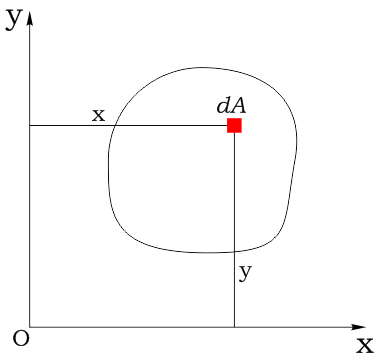
Координаты площадки обозначим соответственно как x и y:
Статический момент элементарной площадки:
Суммируя выражения по всей площади фигуры, получим соответственно:
Единица измерения статического момента [м3].
Пусть xC ,yC координаты центра тяжести C фигуры
тогда статические моменты относительно осей x и y:
Положение центра тяжести >
Моменты инерции плоских сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Геометрические свойства сечений являются показателями конструктивных характеристик и несущей способности сечений. Они нужны для расчета прочности, устойчивости, изгибных и сдвиговых напряжений, прогибов — важных факторов в процессе общего проектирования конструкций мостов. Характеризуются формой и размерами сечений независимо от свойств материала.
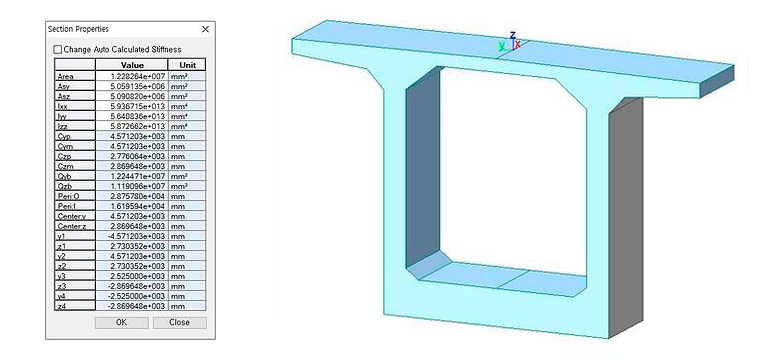
В этой статье мы рассмотрим, как можно вычислить эти свойства сечений самостоятельно «в ручном режиме». В конце статьи вы можете скачать два калькулятора свойств двутаврового и коробчатого сечений в формате Excel для самостоятельного использования. А если вы хотите полностью избежать утомительной работы и сэкономить время, избежать повторяющихся задач и рутины — используйте программный комплекс midas Civil. В нем свойства сечений вычисляются автоматически.
Рисунок 1. Свойства коробчатого сечения, которые вычисляются в midas Civil
Давайте рассмотрим среди свойств сечения соотношение между центром тяжести сечения, статическим моментом площади сечения и моментом инерции, применяемым в формулах изгибных и сдвиговых напряжений, и то, как эти величины можно вычислить.
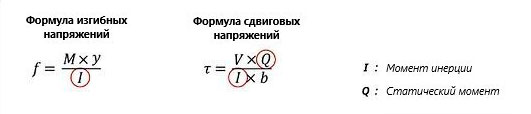
Статический момент площади сечения и центр тяжести
Статический момент площади используется для расчета центра тяжести сечений и касательного напряжения балочных элементов.
-
Формулу можно получить следующим образом:
Линейная область, удовлетворяющая закону Гука, подтверждается при помощи диаграммы отношения между напряжением и деформацией. Отношение между напряжением и деформацией материала с линейным упругим поведением может быть выражено наряду с соотношением между деформацией и кривизной.
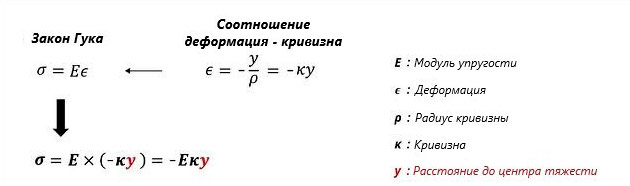
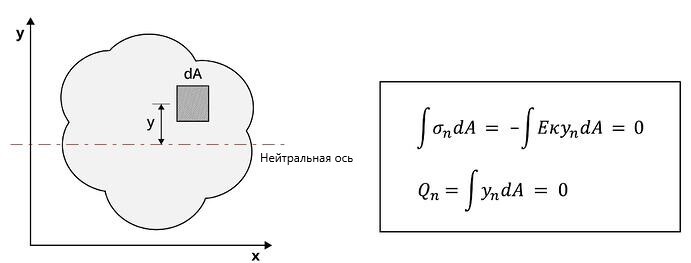
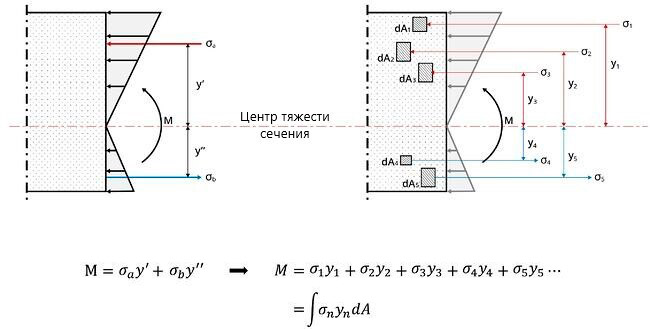
Применив указанное выражение к сечению, в котором действует только изгиб без осевых усилий, как показано на изображении ниже, можно получить выражение, которым вычисляют статический момент площади сечения. Таким образом, сумма нормальных напряжений равна нулю, поскольку действует только изгиб без осевых усилий.
Напряжение «σ1», которое действует на элемент, расположенный на расстоянии «y» от нейтральной оси, и бесконечно малую площадь «dA» в пределах сечения, можно вычислить через выражение, приведенное выше. Сумма напряжений, которые действуют на n-бесконечно малые площади, распределенные по всему сечению, равна 0 и может быть выражена следующим образом. Поскольку кривизна и модуль упругости «E» являются ненулевыми константами, интеграл произведения «dA» и «y» должен быть равен 0.
Из приведенного расчета можно понять, что в случае использования линейно-упругих материалов нейтральная ось становится центром тяжести поперечного сечения; при этом статический момент площади сечения по отношению к центру тяжести сечения равен 0.
Рисунок 2. Выведение формулы статического момента площади сечения
С помощью показанного на Рисунке 2 выражения можно вычислить статический момент площади сечения и расположение центра тяжести поперечного сечения для тех случаев, когда ось «x» выступает в качестве их базисной оси.
Примеры вычисления статического момента площади
Пример 1
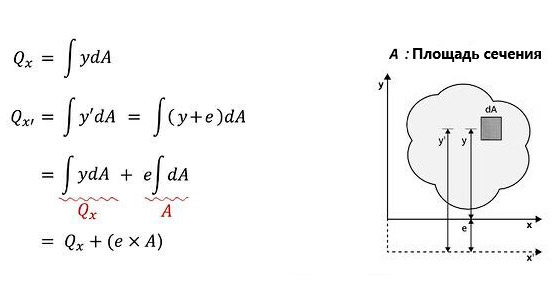
- Вычислив статический момент площади сечения относительно оси «x’», которая расположена на расстоянии «e» от координатной оси «x». Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e».
- Расстояние «y’» — расстояние от оси «x’» до соответствующего элемента, можно учитывать отдельно как «y» и «e».
Пример 2
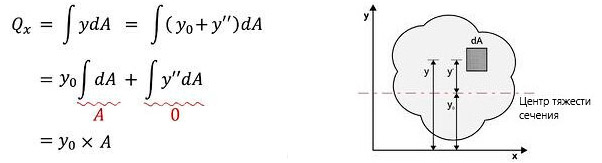
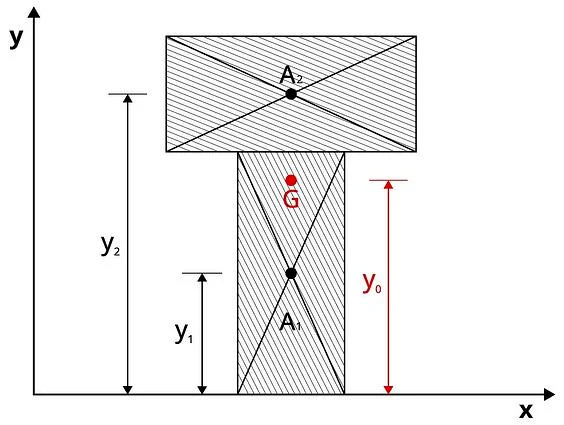
- В этом примере ось «x» задается в качестве базисной оси, и статический момент площади сечения можно вычислить путем вычленения из «y» величин «y0», которая представляет собой расстояние от оси «x» до центра тяжести поперечного сечения, и «y”», которая является расстоянием от центра тяжести поперечного сечения до произвольной области.
- Поскольку статический момент площади сечения от центра тяжести поперечного сечения равен «0», величина «y”» становится «0».
- Таким образом, статический момент площади сечения вычисляется путем умножения общей площади поперечного сечения на значение расстояния от оси «x» до центра тяжести поперечного сечения.
- Следует отметить, что статический момент площади сечения можно вычислить путем умножения общей площади поперечного сечения на расстояние от координатной оси до центра тяжести поперечного сечения.
Пример 3
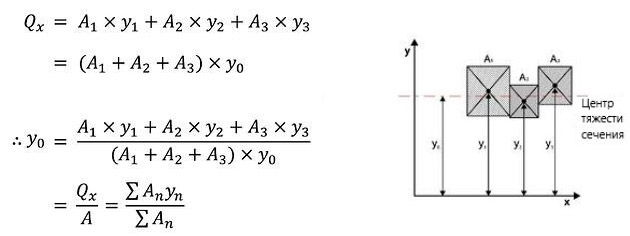
- Статический момент площади сечения можно рассчитать путем сложения произведения площади каждого сечения и расстояния от оси «x» до центра тяжести поперечного сечения.
- Когда известно место расположения центра тяжести поперечного сечения, и когда эти три сечения объединены, статический момент площади сечения можно вычислить как произведение общей площади поперечного сечения и «y0», как показано на примере.
- Из полученного результата можно вывести обобщенное выражение, которое позволит найти центр тяжести поперечного сечения через статический момент площади сечения.
Обобщенную формулу центра тяжести поперечного сечения можно сопоставить с результатами непосредственного расчета центра тяжести поперечного сечения через условия равновесия. Метод расчета расстояния «y0» от координатной оси до центра тяжести поперечного сечения «G» выглядит так:
Рисунок 3: Формула центра тяжести поперечного сечения и применение уравнений равновесия
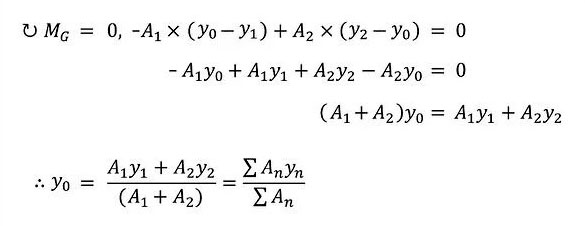
Формула центра тяжести поперечного сечения, полученная через условия равновесия, представляет собой ту же формулу, которая была получена через статический момент площади сечения.
Момент инерции площади поперечного сечения
Момент инерции используется в качестве критерия для определения изгибной жесткости сечения и расчета прогибов, изгибных напряжений и касательных напряжений конструкций. Формулу расчета момента инерции можно получить как соотношение между моментом и кривизной, а также в результате вычисления этого соотношения.
Как показано на Рисунке 4, сумма моментов, создаваемых нормальными напряжениями, которые воздействуют на сечение, равна моменту «M». Эту формулу можно преобразовать в уравнение для напряжения, которое воздействует на сечение, разделенное на n-бесконечно малых элементов. При этом обобщенная формула выглядит так:
Рисунок 4. Выведение формулы момента инерции
В случае, если полученную выше формулу заменить формулой расчета напряжений линейно-упругого материала, она будет выражена следующим образом: выражение суммы произведения квадрата «y» и площади поперечного сечения называется моментом инерции и обозначается как «I». Поскольку момент инерции является произведением длины в квадрате и площади поперечного сечения, единица выражена как длина в четвертой степени.
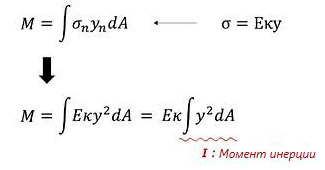
Приведенная выше формула суммируется для кривизны и момента следующим образом: кривизна «κ» пропорциональна моменту и обратно пропорциональна изгибной жесткости «EI». Изгибная жесткость «EI» применяется в качестве стандарта для измерения уровня, на котором элемент конструкции может противостоять изгибу. Благодаря этой формуле можно понять, что модуль упругости и форма, представляющие собой внутренние физические свойства элементов конструкции, являются важными факторами, которые определяют прочность конструкций.

Когда используется материал с большим модулем упругости или поперечное сечение с большим моментом инерции площади, изгибная жесткость увеличивается. С увеличением изгибной жесткости повышается способность конструкции противостоять изгибу, при этом уменьшается ее прогиб, так как угол прогиба или отклонения и момент инерции площади сечения обратно пропорциональны.
Формулу расчета момента инерции площади сечения, полученную указанным способом, можно обобщить на Рисунке 5. Момент инерции площади произвольного сечения при оси «x» в качестве координатной оси рассчитывается следующим образом: расстояние от координатной оси «x» до центра тяжести площади сечения составляет «r», а расстояние от центра тяжести площади сечения до n-бесконечно малых элементов можно подразделить на «yn».
Рисунок 5. Теорема о параллельном переносе осей для момента инерции
Поскольку статический момент площади сечения «QG», вычисляемый как интегральное произведение «yn» и бесконечно малой площади «dA», равен 0, то момент инерции относительно оси «x» можно вычислить как сумму момента инерции «I» и произведение «r2» и площади поперечного сечения «A». Кроме того, площадь поперечного сечения «A» и «r2» всегда являются положительными величинами. Поэтому, когда координатная ось принимается как центр тяжести поперечного сечения, моментом инерции становится наименьшее значение.
Момент инерции обозначен как «I», когда координатной осью является центр тяжести поперечного сечения, и как «Ix», когда координатной осью является ось «x». Из приведенного выше процесса выведения видно, что значение момента инерции варьируется в зависимости от координатной оси. Перемещение координатной оси от центра тяжести поперечного сечения к оси «x» с целью получения обобщенного выражения момента инерции площади сечения сообразно с координатной осью называется теоремой о параллельном переносе осей.
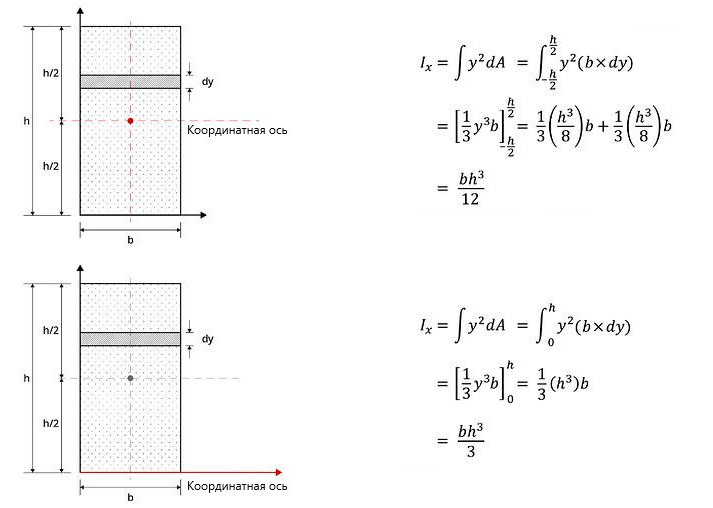
По прямоугольному сечению на Рисунке 6 можно проверить, как момент инерции площади сечения варьируется сообразно с координатной осью.
Рисунок 6. Пример изменения момента инерции в зависимости от местоположения координатной оси
Можно наблюдать, насколько отличается момент инерции прямоугольного сечения, когда координатная ось расположена в центре тяжести поперечного сечения и когда координатная ось расположена по оси x.
Калькуляторы свойств коробчатого сечения и двутаврового сечения в Excel
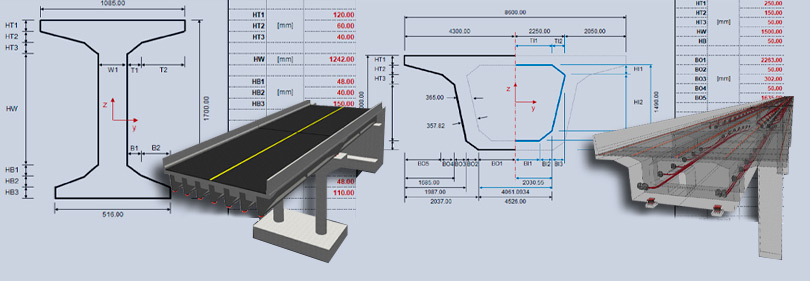
В разделе «Поддержка – Пособия – Калькуляторы» вы можете скачать шаблоны калькуляторов свойств двутаврового и коробчатого сечения в формате Excel. Просто вводите требуемые размеры сечений и получайте результаты для центра тяжести поперечного сечения, момента инерции площади поперечного сечения и момента инерции двутавровых сечений.

|
Глава 2. Геометрические |
||
|
характеристики поперечных сечений |
||
|
Известны три геометрические характеристики, знакомые каждому — это длина, |
||
|
площадь, объем, которые имеют определенный физический смысл. В этой главе |
||
|
рассмотрим новые характеристики, которые будут использоваться в расчетных |
||
|
формулах сопротивления материалов: статические моменты и моменты инерции |
||
|
площади сечений. Эти характеристики не имеют физического смысла. Их нельзя |
||
|
измерить. |
||
|
При выводе формул сопротивления материалов иногда случается, что часть формулы |
||
|
представляет собой интегральное выражение, зависящее только от формы и размеров |
||
|
сечения. Для упрощения последующего использования таких формул удобно такое |
||
|
выражение подсчитать заранее для различных форм сечений. |
||
|
Статические моменты площади сечений используются при определении положения |
||
|
центра тяжести сечения, при расчете касательных напряжений при изгибе. |
||
|
Моменты инерции используются при расчете напряжений и перемещений при изгибе |
||
|
и при кручении и т. д. |
||
|
Статическими моментами площади сечений называются интегралы следующего вида |
||
|
Sy = ∫ z2dA |
||
|
A |
(2.1) |
|
|
Sz = ∫ y2dA |
||
|
A |
||
|
У статических моментов нет физического смысла, но есть геометрическая |
||
|
интерпретация. |
||
|
Рассмотрим сечение произвольной формы (рис. 2.1). |
||
|
Рис.2.1. Геометрическая интерпретация статических моментов площади сечений |
Выделим в сечении элементарную площадку dA с координатами y и z . Произведение площади dA на координату y есть элементарный статический момент dSz относительно оси z .Это понятие аналогично моменту силы
относительно оси. Если предположить, что A — это вес пластины, имеющей форму нашего сечения, то статический момент Sz — это момент силы тяжести пластины
относительно оси z .
2.1.1. Свойства статических моментов площади сечения
Размерность статических моментов — длина3 , обычно м3 или см3 .
Статические моменты могут быть положительными, отрицательными или равными нулю.
Ось, относительно которой статический момент равен нулю, называется
центральной.
Точка пересечения центральных осей называется центром тяжести сечения.
Статический момент составного сечения равен сумме статических моментов элементов этого сечения .
Это вытекает из свойств определенного интеграла, который можно вычислять по частям (в нашем случае по частям площади A ).

2.1.2. Определение положения центра тяжести |
||||||
|
Рассмотрим изменение статического момента при параллельном переносе осей |
||||||
|
координат (рис. 2.2). Расстояние между старыми и новыми осями координат |
||||||
|
обозначим a и b . Пусть известны статические моменты относительно старых осей |
||||||
|
координат |
z – y . |
Найти |
статические |
моменты |
относительно |
параллельно |
|
перенесенных осей координат z1 – y1 . |
||||||
|
Рис.2.2. К определению статических моментов относительно параллельно перенесенных осей |
|
По определению |
Sz1 = ∫ y1dA |
Sy1 = ∫ z1dA . |
|
A |
A |
Выделим элементарную площадку dA и запишем связь между координатами
|
площадки в старой и новой системах координат z1 = z − b |
y1 = y − a . |
||||||||||||
|
Тогда |
Sz1 |
= ∫(y − a)dA = ∫ ydA − a∫dA = Sz |
− aA |
||||||||||
|
A |
A |
A |
|||||||||||
|
Аналогично |
Sy1 |
= ∫(z − a)dA = ∫zdA − b∫dA = Sy − bA . |
|||||||||||
|
A |
A |
A |
|||||||||||
|
Найдем, на сколько надо сместить оси, чтобы они стали центральными. |
|||||||||||||
|
S |
z |
= S |
z |
− aA = 0 , |
a = y |
c |
= |
Sz |
, |
||||
|
A |
|||||||||||||
|
1 |
|||||||||||||
|
Sy |
= Sy − bA = 0 , |
b = zc |
= |
Sy |
. |
||||||||
|
1 |
A |
||||||||||||
Здесь yc и zc — координаты центра тяжести, но найти их пока нельзя, ведь Sz и Sy неизвестны.
Чтобы найти их, используем способ Мюнхгаузена, который сам себя за волосы из болота вытащил.
Если не известны координаты центра тяжести всего сечения, то разобьем его на такие элементы, для которых эти координаты известны без расчетов, это — прямоугольник, круг, треугольник.
Рис. 2.3. Определение статических моментов составной фигуры
На рисунке 2.3 сечение разбито на три прямоугольника Статический момент каждого элемента найдем по предыдущей формуле Sz = yc A и Sy = zc A .
Суммарный статический момент всего сечения равен сумме статических моментов элементов этого сечения (по третьему свойству статических моментов)
Sz = Sz1 + Sz2 + Sz3 = A1 y1 + A2 y2 + A3 y3 Sy = Sy1 + Sy2 + Sy3 = Ay1 z1 + Ay2 z2 + A3 z3 .
или Sz = ∑Szi и Sy = ∑Syi .
В прошлой статье “цикла в цикле” мы разобрали площадь сечения, кратко коснулись её использования для определения напряжений и повторили как с помощью интегрирования определить площадь сложного сечения. В этой статье речь пойдет о статических моментах. И первое, что стоит о них сказать — это то, что, в отличие от площади и размеров сечения, статический момент достаточно абстрактная величина, то есть их нельзя измерить неким прибором, увидеть или ощутить тактильно. Единственный путь определения статического момента — бусидо расчет. Однако для того, чтобы получить ответ на вопрос “сломается ли деталь” при изгибах и кручении, эта величина очень удобна.
Сначала немного теории
Проясним физический смысл величины.
Статические моменты выражают действие момента собственного веса стержня относительно некоторых осей. Впрочем, тут стоит всё же разобраться более подробно:
Представим, что у нас есть стержень какого-то сложного сечения. Мы также произвольно построим систему координат (но желательно всё же, чтобы она проходила близко к сечению нашего стержня). А теперь важный момент: стержень жестко закреплен основанием на осях, которыми мы задались.
На такой стержень действует сила тяжести, вызывая момент. Что это такое мы уже выяснили в части, посвященной изгибу. Для тех, кто заметку про изгиб не читал: момент силы — это произведение силы на плечо (расстояние от точки приложения силы до рассматриваемой точки). Для всего стержня он будет:
g – ускорение свободного падения
ρ – плотность (объёмный вес) материала стержня
l – длина стержня
e – плечо момента. Если стержень “закреплен” на оси, то плечо будет равно расстоянию до этой оси (x или y). е — потому что эксцентриситет!
F – площадь поперечного сечения стержня.
При этом мы можем заметить следующее:
- Плотность материала для любого куска стержня пусть будет одинакова, как и его длина, а значит они вместе с ускорением свободного падения будут константами для моментов каждой точки поперечного сечения стержня и не повлияют на разницу в величине моментов разных точек. По сути, их можно вынести за скобки и рассматривать только произведение площади на расстояние до оси.
- Если расстояние до осей не очень велико по сравнению с размерами сечения, то каждая материальная точка будет иметь свой момент (потому что точки находятся на неодинаковом расстоянии до оси). Это значит, что для определения момента от собственного веса нужно разделить сечение на как можно большее количество элементарных площадок, умножить площадь каждой из них на расстояние до оси и, затем, просуммировать получившиеся произведения.
А сумма произведений предельно малых площадей сечения на расстояние до оси – это интеграл, следовательнодля определения моментов относительно системы координат xOy нам необходимо прежде всего вычислить такие два интеграла:
Каждый из этих интегралов как раз и представляет собой сумму произведений элементарных площадок dF на расстояние до соответствующей оси (x или y).
Элементарная площадка – это кусок сечения с очень малой площадью. Настолько малой, что она меньше всякой возможности её измерить и меньше всякого конечного значения вообще. Но нулю она не равна.
Эти интегралы называются соответственно – статические моменты сечения относительно осей x и y.
Статический момент может быть как положительным, так и отрицательным. Величина статического момента зависит от выбора системы координат. Имеет размерность см3.
Теперь попробуем параллельно перенести оси так, чтобы расстояния между ними были a и b. Теперь x1=x-a, y1=y-b. Изменятся ли статические моменты в таком случае? Если изменятся, то как? И что нам может дать такое изменение расположения осей? Давайте посмотрим:
Значит при переносе осей без их поворота статический момент изменяется на величину, равную произведению площади всего сечения на расстояние между осями.
Можно подобрать оси (а, следовательно и величины a и b) так, что b*F=Sx и a*F=Sy .
В таком случае статический момент сечения относительно осей будет равен нулю. Такие оси будут называться центральными, а начало отсчета такой системы координат – центром тяжести сечения.
Т.е. статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если оно закреплено (опирается) в точке центра тяжести. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение равно нулю.
Тут нам важно одно свойство центра тяжести – если сечение имеет ось симметрии, то центр тяжести всегда лежит на ней. Если осей симметрии целых две, (а они вообще-то должны пересекаться) то точка их пересечения – центр тяжести. Следовательно чтобы найти статический момент сложного сечения, состоящего из нескольких простых, симметричных – нужно найти его центр тяжести из выражений:
х1, y1 и x2, y2 – это координаты центров тяжести простых сечений, входящих в состав сложного.
После преобразования получим формулы для координат центра тяжести:
Далее, нужно непосредственно найти статический момент:
Где, x’ и y’ – оси, относительно которых нужно найти статический момент.
Находим статический момент
Пример:
Найти статический момент сечения неравнополочного уголка 14/9 толщиной 10 мм по ГОСТ 8510-86 без учета скруглений относительно осей, указанных на рисунке:
Определим площади и положение центров тяжести двух частей сечения – прямоугольников 130х10 и 90х10:
Координаты центра тяжести сечения определяем по формулам:
Если перенести ось Х на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 4.58 см.
Если перенести ось Y на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 2.12 см.
Найдем статические моменты сечения:
Подведём итоги
Статический момент — величина, характеризующая положение выбранных осей относительно центра тяжести сечения. Статический момент относительно центра тяжести равен нулю. Посчитать его мы можем как произведение площади сечения на расстояние от центра сечения до выбранной оси, но когда расстояние до оси сравнимо с размерами сечения нужно всё же взять интеграл.
Статический момент, кроме определения центра тяжести, используется для расчётов касательных напряжений, что на практике выливается также в расчеты на скалывание (конструкций из дерева).
На очереди моменты инерции.
Автор: Марк Ершов
Редактор, факт-чекер: Кирилл Овчинников
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 670