Статисти́ческий вес — физическая величина, определяющая в квантовой механике и квантовой статистике количество различных квантовых состояний системы с одинаковой энергией (синоним: кратность вырождения энергетического уровня). В статистической физике и термодинамике статистическим весом называют количество способов (микросостояний системы), которыми может быть реализовано данное макроскопическое состояние статистической системы. Статистический вес обычно обозначается символами Γ, g, w, W или Ω.
По вышеприведённому определению, статистический вес является безразмерным целым числом, большим или равным единице, 
При рассмотрении квантовых систем с непрерывным спектром энергии под статистическим весом обычно понимают количество квантовых состояний, приходящихся на определённый энергетический интервал. В таком определении статвес имеет размерность обратной энергии.
В квазиклассическом приближении мерой статистического веса служит фазовый объём системы, приходящийся на определённый интервал энергии. Если система имеет n степеней свободы, то фазовый объём и соответствующий статистический вес выражается в единицах hn, где h — постоянная Планка.
Энтропия S системы и её статистический вес связаны соотношением Больцмана: S = k ln w (здесь k — постоянная Больцмана).
Статистический вес, определённый через фазовый объём или число микросостояний, является мультипликативной физической величиной: если система состоит из двух невзаимодействующих подсистем со статвесами w1 и w2, то общий статистический вес системы W = w1w2.
См. также[править | править код]
- Статистическая сумма
Литература[править | править код]
- Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
- Degeneracy. In: IUPAC. Compendium of Chemical Terminology, 2nd ed. (the «Gold Book»). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006-) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. doi:10.1351/goldbook.
Прежде чем перейти
к рассмотрению распределения Гиббса,
введем два важнейших понятия статистической
физики: макро- и микросостояния и
статистический вес макроскопической
системы.
Как уже отмечалось,
в термодинамике состояние макроскопической
системы определяется небольшим числом
параметров, таких, например, как
температура, давление, объем и др. Эти
параметры называют макроскопическими
параметрами, так как они определяют
состояние всей системы в целом, а не
отдельной ее молекулы и могут быть
измерены макроприборами. Состояние,
определенное с помощью указанных
параметров, называется макросостоянием
(или термодинамическим состоянием).
С другой стороны,
всякая термодинамическая система
представляет собой совокупность большого
числа частиц (атомов, молекул, ионов и
т.д.). Поэтому состояние термодинамической
системы (например, газа) в принципе может
быть определено с помощью состояний
каждой из ее частиц, т.е. их положения и
импульса. Состояние каждой частицы как
отдельной материальной точки, определяется
шестью параметрами: тремя координатами
и тремя проекциями импульса. Причем эти
два состояния считаются различимыми,
если разности их координат и соответствующих
проекций импульса будут не меньше тех,
которые определяются соотношениями
неопределенностей. Следовательно, для
определения состояния системы состоящей
из N
частиц, нужно знать 6N
параметров их механического движения.
В квантовом случае состояние отдельной
частицы определяется заданием квантовых
чисел α,
определяющих энергию и другие динамические
характеристики частицы. Эти числа
получаются из решения соответствующего
уравнения Шредингера. Состояние системы,
определенное заданием состояния всех
образующих систему частиц, называется
ее микросостоянием. Поскольку любая
частица является квантовым объектом,
то квантовым объектом является и вся
термодинамическая система. Поэтому ее
микросостояние должно описываться с
помощью квантовой механики. Для этого
необходимо определить уровни энергии

кратность их вырождения и набор квантовых
чисел

Когда термодинамическая
система находится в равновесии и ее
макроскопические параметры фиксированы,
с микроскопической точки зрения ее
состояние не определено. Всякое
макросостояние может быть осуществлено
различными способами, каждому из которых
соответствует некоторое микросостояние
системы. Возможно очень большое число
различных микросостояний, доступных
системе при заданных ее макроскопических
параметрах. Число микросостояний,
соответствующих данному макросостоянию,
называется статистическим весом
макросостояни и обозначается W.
При изменении макросостояния (при
изменении ее термодинамических
параметров) изменяется и его статистический
вес. Поэтому статистический вес
макросостояния зависит от параметров
состояния, т.е. является функцией
состояния системы.
Статистический
вес обладает свойством мультипликативности.
Пусть W1
и W2
– статистические веса двух слабо
взаимодействующих систем. Тогда
статистический вес

объединенной системы будет равен

Это следует из того, что для каждого
возможного состояния первой системы
существует W2
состояний второй, так что число состояний
объединенной системы
будет

Таких слагаемых будет W1.
Следовательно,
При определении
статистического веса произвольной
системы поступают так же, как при
определении числа состояний одной
частицы в квазиклассическом приближении.
Вводят f-мерное
фазовое пространство системы, где f
– число степеней свободы системы (в
случае идеального одноатомного газа f
= 6N).
На каждое состояние системы в таком
пространстве принимается фазовая ячейка
объемом
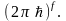
Тогда
если объем фазового пространства,
соответствующий энергии системы, не
превышающей некоторого значения E,
равен

то число микросостояний с указанной
энергией найдется как

а число микросостояний с энергией от E
до E + dE
– как

где
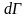
– объем фазового пространства,
соответствующий указанному интервалу
энергий.
Любое микросостояние
термодинамической системы реализуется
не с полной достоверностью, а имеет
определенную вероятность его реализации.
Очевидно, чем больше число способов
осуществления того или иного макросостояния,
тем оно вероятнее. Таким числом способов
является число микросостояний, т.е.
статистический вес W
макросостояния. Следовательно, вероятность
реализации макросостояния системы
пропорциональна числу микросостояний
с ним совместных: p

~ W,
где W0
– общее число микросостояний системы.
Таким образом, статистический вес
определяет вероятность термодинамического
состояния; по этой причине его часто
называют термодинамической вероятностью.
Заметим, однако, что в отличие от
математической вероятности, которая
не может превышать единицы, термодинамическая
вероятность (статистический вес)
выражается большими числами.
Чем выше
статистический вес состояния системы,
тем более оно вероятно и тем чаще оно
реализуется. Отсюда следует, что если
возможны два состояния с различными
статистическими весами и в какой-то
момент времени изолированная система
оказалась в состоянии с меньшим
статистическим весом, то наиболее
вероятным развитием данной системы
является переход ее в будущем в состояние
с большим статистическим весом. Наиболее
вероятным состоянием изолированной
системы является состояние равновесия.
Поэтому в состоянии равновесия
изолированная система имеет максимально
возможное для данного состояния значение
статистического веса.
В статистической
физике распределение Больцмана по
энергии частицы обобщается на случай
распределения по энергии любой
макроскопической системы. В случае
дискретного спектра энергии определяют
вероятность того, что система обладает
энергией

(находится на i-ом
энергетическом уровне или, что то же
самое, в одном из микросостояний с
энергией
).
Эта вероятность имеет вид

(3.26)
где

– кратность вырождения i-го
уровня системы, число микросостояний
с данным значением энергии – статистический
вес системы;

–
сумма по состояниям
системы, ее называют статистической
суммой системы.
В квазиклассическом
приближении (в случае непрерывного
спектра) определяют вероятность того,
что макроскопическая система обладает
энергией из интервала от E
до E + dE.
В этом случае имеем

(3.27)
где

–
число микросостояний системы в указанном
интервале энергии,

71
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
Состояние макроскопического тела (т. е. тела, образованного огромным количеством молекул) может быть задано с помощью объема, давления, температуры, внутренней энергии и других макроскопических (т. е. характеризующих все тело в целом) величин.
Охарактеризованное таким способом состояние называется макросостоянием.
Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием.
Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствует некоторое микросостояние тела. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом или термодинамической вероятностью макросостояния. Таким образом, статистический вес представляет собой число микроскопических способов, которыми может быть осуществлено данное макросостояние.
Чтобы пояснить понятие статистического веса, рассмотрим способы, которыми молекулы газа могут распределяться между двумя половинами сосуда, в котором заключен газ. Пусть общее число молекул равно N. В качестве характеристики состояния газа примем число молекул, находящихся в левой половине сосуда, которое мы обозначим буквой  (соответственно число молекул в правой половине сосуда будет равно
(соответственно число молекул в правой половине сосуда будет равно  ). Состояние отдельной молекулы будем характеризовать указанием на то, в какой из половин сосуда она находится. Такое описание состояния газа и состояний отдельных молекул является, конечно, далеко не полным. Однако оно достаточно для того, чтобы выяснить на этом примере характерные особенности статистического поведения любых макросистем.
). Состояние отдельной молекулы будем характеризовать указанием на то, в какой из половин сосуда она находится. Такое описание состояния газа и состояний отдельных молекул является, конечно, далеко не полным. Однако оно достаточно для того, чтобы выяснить на этом примере характерные особенности статистического поведения любых макросистем.
Начнем со случая, когда полное число молекул равно четырем (рис. 102.1). Каждая молекула с равной вероятностью может находиться как в левой, так и в правой половине сосуда. Поэтому вероятность того, что, скажем, молекула 1 окажется в левой половине сосуда, Р/авна 1/2. Пребывание в левой половине сосуда молекулы 1 и пребывание в той же половине сосуда молекулы 2 являются статистически независимыми событиями. Поэтому вероятность одновременного нахождения в левой части сосуда молекул 1 к 2 равна произведению вероятностей, т. е.  . Продолжая эти рассуждения, получим, что вероятность одновременного нахождения в левой половине сосуда всех четырех молекул равна (1/2).
. Продолжая эти рассуждения, получим, что вероятность одновременного нахождения в левой половине сосуда всех четырех молекул равна (1/2).
Аналогичные рассуждения дают, что вероятность любого размещения молекул в сосуде (скажем такого, при котором 1-я и 4-я молекулы будут находиться в левой половине сосуда, а 2-я и 3-я — в правой), также равна (1/2). Каждое из размещений представляет собой некоторое микросостояние газа.

Рис. 102.1.
Из сказанного выше следует, что вероятность всех микросостояний одинакова и равна 
В табл. 102.1 приведены все мыслимые способы распределения молекул между половинами сосуда (все микросостояния газа). Состояние, характеризуемое тем, что, скажем, в левой части сосуда находится одна молекула (безразлично какая), а в правой части — три молекулы, представляет собой макросостояние.
Таблица 102.1

Из таблицы видно, что такому макросостоянию соответствует 4 микросостояния. Следовательно, статистический вес данного макросостояния равен 4, а вероятность (обычная, а не термодинамическая) равна 4/16. Макросостояпие, при котором в обеих частях сосуда находится одинаковое число молекул, реализуется с помощью шести микросостояний.
Соответственно его статистический вес равен 6, а вероятность (обычная) равна 6/16.
Из рассмотренного примера вытекает, что все микросостояния данной системы равновероятны, вследствие чего статистический вес оказывается пропорциональным вероятности (обычной) макросостояния. Утверждение о равновероятности всех микросостояний лежит в основе статистической физики и носит название эргодической гипотезы.
Согласно табл. 102.1 в случае четырех молекул имеется большая вероятность (равная 1/8) того, что все молекулы соберутся в одной из половин сосуда (левой или правой). Однако с увеличением числа молекул положение существенно меняется.
Найдем число способов (число микросостояний), посредством которых может быть осуществлено макросостояние, характеризуемое тем, что в левой половине сосуда окажется  молекул из общего числа их N, а в правой половине — (
молекул из общего числа их N, а в правой половине — ( ) молекул. Для этого пронумеруем молекулы, приписав им номера от 1 до N. Затем станем отбирать по одной молекуле и помещать их в левую половину сосуда. Первую молекулу можно выбрать N способами, вторую — (N—1) способом, третью — (N—2) способами, наконец,
) молекул. Для этого пронумеруем молекулы, приписав им номера от 1 до N. Затем станем отбирать по одной молекуле и помещать их в левую половину сосуда. Первую молекулу можно выбрать N способами, вторую — (N—1) способом, третью — (N—2) способами, наконец,  молекулу можно выбрать (
молекулу можно выбрать ( ) способом. Оставшиеся (N—n) молекул поместим в правую половину сосуда.
) способом. Оставшиеся (N—n) молекул поместим в правую половину сосуда.
Из сказанного выше следует, что число  способов, с помощью которых можно отобрать случайным образом из общего числа N молекул
способов, с помощью которых можно отобрать случайным образом из общего числа N молекул  молекул для левой половины сосуда, равно
молекул для левой половины сосуда, равно

Домножив и разделив это число на  получим выражение
получим выражение

Однако не все  способов приводят к отличающимся друг от друга микросостояниям. Отдельные микросостояния отличаются только совокупностью номеров молекул, отобранных для каждой из половин сосуда, но не последовательностью, в которой эти молекулы отбирались. Например, при
способов приводят к отличающимся друг от друга микросостояниям. Отдельные микросостояния отличаются только совокупностью номеров молекул, отобранных для каждой из половин сосуда, но не последовательностью, в которой эти молекулы отбирались. Например, при  получаются выборки
получаются выборки

Из них выборки 1—2 и 2—1 отвечают одному и тому же микросостоянию (в левой половине 1-я и 2-я молекулы, в правой — 3-я). То же самое относится к выборкам 1—3 и 3—1, а также 2—3 и 3—2. Таким образом, выборки, отличающиеся только перестановкой  номеров молекул, отобранных для левой половины сосуда (таких выборок
номеров молекул, отобранных для левой половины сосуда (таких выборок  ), соответствуют одному и тому же микросостоянию.
), соответствуют одному и тому же микросостоянию.
Следовательно, чтобы получить число микросостояпий, с помощью которых может быть осуществлено макросостояшге  нужно разделить число (102.1) на
нужно разделить число (102.1) на  . В результате для статистического веса получается выражение
. В результате для статистического веса получается выражение

Легко убедиться в том, что  (см. табл. 102.1).
(см. табл. 102.1).
В табл. 102.2 приведены значения Q, вычисленные по формуле (102.2) для случая  Полное число способов распределения 24 молекул между двумя половинами сосуда равно 224—16 777 216, и только в двух случаях все молекулы оказываются сосредоточенными в одной из половин сосуда. Вероятность такого события равна примерно
Полное число способов распределения 24 молекул между двумя половинами сосуда равно 224—16 777 216, и только в двух случаях все молекулы оказываются сосредоточенными в одной из половин сосуда. Вероятность такого события равна примерно  . В четырех кубических сантиметрах воздуха содержится около
. В четырех кубических сантиметрах воздуха содержится около  молекул. Вероятность того, что все эти молекулы соберутся в одной из половин сосуда, равна двум, деленным на два в степени
молекул. Вероятность того, что все эти молекулы соберутся в одной из половин сосуда, равна двум, деленным на два в степени  что составляет приблизительно
что составляет приблизительно  . Эта вероятность настолько мала, что практически ее можно считать равной нулю.
. Эта вероятность настолько мала, что практически ее можно считать равной нулю.

Рис. 102.2.
Таблица 102.2

На рис. 102.2 изображен график, показывающий, как меняется число молекул  в одной из половин сосуда с течением времени. Это число колеблется около среднего значения, равного
в одной из половин сосуда с течением времени. Это число колеблется около среднего значения, равного  .
.
Случайные отклонения значений какой-либо физической величины х от ее среднего значения  называются флуктуациями этой величины. Обозначив флуктуацию через
называются флуктуациями этой величины. Обозначив флуктуацию через  получим, что
получим, что
 (102.3)
(102.3)
Среднее арифметическое величины (102.3) равно нулю. Действительно,

Поэтому в качестве характеристики флуктуаций берут среднюю квадратичную флуктуацию, равную
 (102.4)
(102.4)
Более показательна относительная флуктуация величины х, которая определяется отношением
 (102.5)
(102.5)
В статистической физике доказывается, что относительная флуктуация аддитивной величины (т. е. такой величины, значение которой для тела равно сумме значений для отдельных его частей) обратно пропорциональна корню квадратному из числа N образующих тело молекул:
 (102.6)
(102.6)
Вычислим на основании данных табл. 102.1 относительную флуктуацию числа молекул в левой половине сосуда. Вычисления будем производить по формуле (93.5). В табл. 102.3 приведены значения флуктуаций и их вероятности Р. В соответствии с этими данными

Следовательно, средняя квадратичная флуктуация равна  а относительная флуктуация равна 1/2 (среднее значение
а относительная флуктуация равна 1/2 (среднее значение  равно 2). Аналогичные вычисления, произведенные с помощью данных табл. 102.2, дают для средней квадратичной флуктуации значение 2,45, а для относительной флуктуации — значение 0,204. Легко убедиться в том, что
равно 2). Аналогичные вычисления, произведенные с помощью данных табл. 102.2, дают для средней квадратичной флуктуации значение 2,45, а для относительной флуктуации — значение 0,204. Легко убедиться в том, что
 (102.7)
(102.7)
Это соотношение согласуется с формулой (102.6).
Из табл. 102.2 следует, что отклонения от среднего числа молекул (равного 12) не более чем на 2 молекулы осуществляются с вероятностью, равной 0,7, а отклонения не более чем на 3 молекулы — с вероятностью, равной 0,85.
Если бы число молекул могло быть дробным, мы могли бы сказать, что большую часть времени газ находится в таких состояниях, в которых отклонения числа молекул от среднего не превышают среднюю квадратичную флуктуацию, т. е. 2,45.
Составив пропорцию, аналогичную (102.7), для  получим относительную флуктуацию
получим относительную флуктуацию  числа молекул в левой половине сосуда для случая, когда
числа молекул в левой половине сосуда для случая, когда  Эта пропорция имеет вид
Эта пропорция имеет вид

откуда  Полученный результат означает, что значение числа молекул в одной из половин сосуда претерпевает изменения, в основном не превышающие единицу десятой значащей цифры.
Полученный результат означает, что значение числа молекул в одной из половин сосуда претерпевает изменения, в основном не превышающие единицу десятой значащей цифры.
Мы рассмотрели флуктуации числа молекул в одной из половин сосуда. Другие макроскопические характеристики, такие, как давление, плотность газа в разных точках пространства и т. д., также испытывают флуктуации, т. е. отклонения от средних значений.
Таблица 102.3

Равновесным является такое макросостояние системы, которое не имеет тенденции к изменению с течением времени. Ясно, что отсутствие такой тенденции будет сильнее всего выражено у наиболее вероятного из всех макросостояний, мыслимых для данной системы. Вероятность состояния пропорциональна его статистическому весу. Поэтому равновесное состояние можно определить как состояние, статистический вес которого максимален.
Система, находящаяся в равновесном состоянии, время от времени самопроизвольно отклоняется от равновесия. Однако эти отклонения являются незначительными и кратковременными. Подавляющую часть времени система проводит в равновесном состоянии, характеризуемом максимальным статистическим весом.
Статистическая физика вскрывает природу необратимых процессов. Предположим, что вначале газ находился в левой половине сосуда, которая отделялась перегородкой от правой пустой половины. Если убрать перегородку, газ самопроизвольно распространится на весь сосуд. Этот процесс будет необратимым, так как вероятность того, что в результате теплового движения все молекулы соберутся в одной из половин сосуда, как мы видели, практически равна нулю. Следовательно, сам по себе, без воздействия извне, газ не сможет снова сосредоточиться в левой половине сосуда.
Таким образом, процесс распространения газа на весь сосуд оказывается необратимым вследствие того, что обратный ему процесс маловероятен. Этот вывод может быть распространен и на другие процессы. Всякий необратимый процесс — это такой процесс, обратный которому крайне маловероятен.
Оглавление
- ПРЕДИСЛОВИЕ
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- ВВЕДЕНИЕ
- ЧАСТЬ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
- § 1. Механическое движение
- § 2. Некоторые сведения о векторах
- § 3. Скорость
- § 4. Ускорение
- § 5. Кинематика вращательного движения
- ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 6. Классическая механика. Границы ее применимости
- § 7. Первый закон Ньютона. Инерциальные системы отсчета
- § 8. Масса и импульс тела
- § 9. Второй закон Ньютона
- § 10. Единицы и размерности физических величин
- § 11. Третий закон Ньютона
- § 12. Принцип относительности Галилея
- § 13. Силы
- § 14. Упругие силы
- § 15. Силы трения.
- § 16, Сила тяжести и вес
- § 17. Практическое применение законов Ньютона
- ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ
- § 18. Сохраняющиеся величины
- § 19. Кинетическая энергия
- § 20. Работа
- § 21. Консервативные силы
- § 22. Потенциальная энергия во внешнем поле сил
- § 23. Потенциальная энергия взаимодействия
- § 24. Закон сохранения энергии
- § 25. Энергия упругой деформации
- § 26. Условия равновесия механической системы
- § 27. Закон сохранения импульса
- § 28. Соударение двух тел
- § 29. Закон сохранения момента импульса
- § 30. Движение в центральном поле сил
- § 31. Задача двух тел
- ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА
- § 32. Силы инерции
- § 33. Центробежная сила инерции
- § 34. Сила Кориолиса
- § 35. Законы сохранения в неинерциальных системах отсчета
- ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА
- § 36. Движение твердого тела
- § 37. Движение центра масс твердого тела
- § 38. Вращение тела вокруг неподвижной оси
- § 39. Момент инерции
- § 40. Понятие о тензоре инерции
- § 41. Кинетическая энергия вращающегося твердого тела
- § 42. Кинетическая энергия тела при плоском движении
- § 43. Применение закона динамики твердого тела
- § 44. Гироскопы
- ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ
- § 45. Закон всемирного тяготения
- § 46. Гравитационное поле
- § 47. Принцип эквивалентности
- § 48. Космические скорости
- ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
- § 49. Общие сведения о колебаниях
- § 50. Малые колебания
- § 51. Комплексные числа
- § 52. Линейные дифференциальные уравнения
- § 53. Гармонические колебания
- § 54. Маятник
- § 55. Векторная диаграмма
- § 56. Биения
- § 57. Сложение взаимно перпендикулярных колебаний
- § 58. Затухающие колебания
- § 59. Автоколебания
- § 60. Вынужденные колебания
- § 61. Параметрический резонанс
- ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА
- § 62. Специальная теория относительности
- § 63. Преобразования Лоренца
- § 64. Следствия из преобразований Лоренца
- § 65. Интервал
- § 66. Преобразование и сложение скоростей
- § 67. Релятивистское выражение для импульса
- § 68. Релятивистское выражение для энергии
- § 69. Преобразования импульса и энергии
- § 70. Взаимосвязь массы и энергии
- § 71. Частицы с нулевой массой покоя
- ГЛАВА IX. ГИДРОДИНАМИКА
- § 72. Линии и трубки тока. Неразрывность струи
- § 73. Уравнение Бернулли
- § 74. Истечение жидкости из отверстия
- § 75. Силы внутреннего трения
- § 76. Ламинарное и турбулентное течения
- § 77. Течение жидкости в круглой трубе
- § 78. Движение тел в жидкостях и газах
- ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 79. Статистическая физика и термодинамика
- § 80. Масса и размеры молекул
- § 81. Состояние системы. Процесс
- § 82. Внутренняя энергия системы
- § 83. Первое начало термодинамики
- § 84. Работа, совершаемая телом при изменениях объема
- § 85. Температура
- § 86. Уравнение состояния идеального газа
- § 87. Внутренняя энергия и теплоемкость идеального газа
- § 88. Уравнение адиабаты идеального газа
- § 89. Политропические процессы
- § 90. Работа, совершаемая идеальным газом при различных процессах
- § 91. Ван-дер-ваальсовский газ
- § 92. Барометрическая формула
- ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА
- § 93. Некоторые сведения из теории вероятностей
- § 94. Характер теплового движения молекул
- § 95. Число ударов молекул о стенку
- § 96. Давление газа на стенку
- § 97. Средняя энергия молекул
- § 98. Распределение Максвелла
- § 99. Экспериментальная проверка закона распределения Максвелла
- § 100. Распределение Больцмана
- § 101. Определение Перреном числа Авогадро
- § 102. Макро- и микросостояния. Статистический вес
- § 103. Энтропия
- ГЛАВА XII. ТЕРМОДИНАМИКА
- § 104. Основные законы термодинамики
- § 105. Цикл Карно
- § 106. Термодинамическая шкала температур
- § 107. Примеры на вычисление энтропии
- § 108. Некоторые применения энтропии
- § 109. Термодинамические потенциалы
- ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
- § 110. Отличительные черты кристаллического состояния
- § 111. Классификация кристаллов
- § 112. Физические типы кристаллических решеток
- § 113. Дефекты в кристаллах
- § 114. Теплоемкость кристаллов
- ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ
- § 115. Строение жидкостей
- § 116. Поверхностное натяжение
- § 117. Давление под изогнутой поверхностью жидкости
- § 118. Явления на границе жидкости и твердого тела
- § 119. Капиллярные явления
- ГЛАВА XV. ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ
- § 121. Испарение и конденсация
- § 122. Равновесие жидкости и насыщенного пара
- § 123. Критическое состояние
- § 124. Пересыщенный пар и перегретая жидкость
- § 125. Плавление и кристаллизация
- § 126. Уравнение Клапейрона—Клаузиуса
- § 127. Тройная точка. Диаграмма состояния
- ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА
- § 128. Явления переноса
- § 129. Средняя длина свободного пробега
- § 130. Диффузия в газах
- § 131. Теплопроводность газов
- § 132. Вязкость газов
- § 133. Ультраразреженные газы
- § 134. Эффузия
- ПРИЛОЖЕНИЯ
- I. Вычисление некоторых интегралов
- II. Формула Стирлинга
- III. Симметричные тензоры второго ранга

