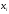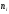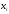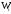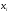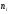Пусть
для изучения количественного (дискретного
или непрерывного) признака Х из генеральной
совокупности извлечена выборка, причем
значение x1
наблюдалось n1
раз, значение x2
наблюдалось n2
раз, …, значение xk
наблюдалось nk
раз.
Наблюдаемые
значения xi
(i
= 1, 2, …, n)
признака Х называют вариантами, а
последовательность всех вариант,
записанных в возрастающем порядке, –
вариационным
рядом.
Числа наблюдений ni
называют частотами,
их сумма
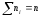 ─объем
─объем
выборки.
Отношения частот к объему выборки
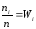 ─относительными
─относительными
частотами.
Статистическим
распределением выборки
называют перечень вариант xi
вариационного ряда и соответствующих
им частот ni
(сумма всех частот равна объему выборки
n)
или относительных частот Wi
(сумма всех относительных частот равна
единице). Статистическое распределение
можно задать также в виде последовательности
интервалов и соответствующих им частот
(в качестве частоты, соответствующей
интервалу, принимают сумму частот,
попавших в этот интервал).
Заметим,
что в теории вероятностей под распределением
понимают соответствие между возможными
значениями случайной величины и их
вероятностями, а в математической
статистике – соответствие между
наблюдаемыми вариантами и их частотами
(или относительными частотами).
Пример.
Задано распределение частот выборки
объема n
= 20:
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
В
данной выборке получены следующие
варианты x1
= 2; x2
= 6; x3
= 12,
соответствующие
частоты n1
= 3; n2
= 10; n3
= 7.
Напишем
распределение относительных частот.
Решение.
Найдем относительные частоты, для чего
разделим частоты на объем выборки
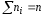 = 3 + 10 + 7 = 20.
= 3 + 10 + 7 = 20.
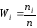
─ относительные
частоты:
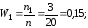
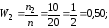

Напишем распределение
относительных частот:
|
|
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Контроль:
сумма всех относительных частот
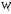 равна единице:
равна единице:
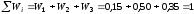 .
.
§14. Эмпирическая функция распределения
Пусть
известно статистическое распределение
частот количественного признака Х.
Введем обозначения:
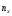 ─
─
число наблюдений, при которых наблюдалось
значение признака, меньше х; n
– общее число наблюдений (объем выборки).
Ясно, что относительная частота события
Х<х равна
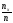 .
.
Если х изменяется, то, вообще говоря,
изменится и относительная частота, то
есть относительная частота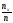 есть функция от х. Так как эта функция
есть функция от х. Так как эта функция
находится эмпирическим (опытным) путем,
то ее называют эмпирической.
Определение.
Эмпирическая
функция распределения
(функция распределения выборки) –
функция F*(x),
определяющая для каждого значения х
относительную частоту события X<x.
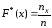 ,
,
где
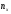 ─ число вариант, меньших х;n
─ число вариант, меньших х;n
– объем выборки.
Например,
для того чтобы найти F*(x2),
надо число вариант, меньших x2,
разделить на объем выборки:
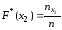 .
.
В
отличие от эмпирической функции
распределения выборки функцию
распределения F(x)
генеральной совокупности называют
теоретической
функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция F(x)
определяет вероятность события X<x,
а эмпирическая функция F*(x)
определяет относительную частоту этого
же события.
Из
теоремы Бернулли следует, что относительная
частота события X<x,
то есть F*(x),
стремится по вероятности к вероятности
этого события, то есть к значению F(x).
Другими словами, при больших значениях
n
числа F*(x)
и F(x)
мало отличаются одно от другого в том
смысле, что
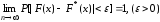 .
.
Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции распределения генеральной
совокупности. Такое заключение
подтверждается и тем, что F*(x)
обладает всеми свойствами F(x).
Из
определения функции F*(x)
вытекают следующие ее свойства:
-
Значения
эмпирической функции принадлежит
отрезку [0; 1]; -
F*(x)
– неубывающая функция; -
Если
x1
─ наименьшая варианта, то F*(x)
= 0 при х < х1;
если
хk
─ наибольшая варианта, то F*(x)
= 1 при х > xk.
Итак,
эмпирическая функция распределения
выборки служит для оценки теоретической
функции распределения генеральной
совокупности.
Пример.
Построить эмпирическую функцию по
данному распределению выборки:
|
Варианты |
2 |
6 |
10 |
|
Частоты |
12 |
18 |
30 |
Решение.
Найдем объем выборки (сумма всех частот
ni):
n
= n1
+ n1
+ n1
= 12 + 18 + 30 = 60.
Наименьшая
варианта равна 2 (x1
= 2), следовательно, F*(x)
= 0 при х ≤ 2 (по свойству 3 функции F*(x));
значения,
меньшие 6 (х<6), а именно x1
= 2, наблюдались n1
= 12 раз, следовательно,
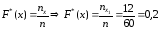 при 2<x≤6;
при 2<x≤6;
значения
х<10, а именно x1
= 2, x1
= 2 наблюдались n1
+ n2
= 12 + 18 = 30 раз, следовательно
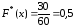 при 6<х≤10.
при 6<х≤10.
Так
как х =10 – наибольшая варианта, то F*(x)
= 1 при х>10 (по свойству 4 функции F*(x)).
Искомая
эмпирическая функция имеет вид:

Ниже приведен график
полученной эмпирической функции.
На графике на
соответствующих осях откладывают
значения функции F*(x)
и интервалы вариант
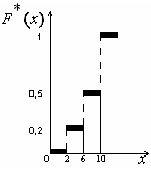
Рис.
5. График эмпирической функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.
Индивидуальное задание 1
Вариант 11
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моду;
- квантильное отклонение;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:
![]()
Эмпирическую функцию распределения определим по формуле
![]()
Здесь nx – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле
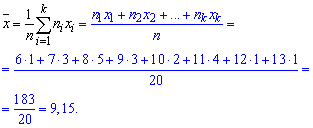
Выборочную дисперсию находим по формуле
![]()
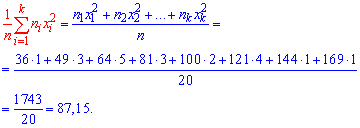
Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу
![]()
Подправленную дисперсию вычисляем согласно формулы
![]()
Выборочное среднее квадратичное отклонение вычисляем по формуле
![]()
Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии
![]()
Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
![]()
Медиану находим по 2 формулам:
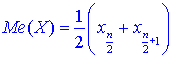 если число n – четное;
если число n – четное;
![]() если число n – нечетное.
если число n – нечетное.
Здесь берем индексы в xi согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому
![]()
Мода – это варианта которая в вариационном ряду случается чаще всего, то есть
![]()
Квантильное отклонение находят по формуле
![]()
где ![]() – первый квантиль,
– первый квантиль, ![]() – третий квантиль.
– третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение
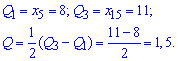
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему
![]()
Коэффициент асимметрии находим по формуле
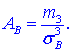
Здесь 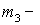 центральный эмпирический момент 3-го порядка,
центральный эмпирический момент 3-го порядка,
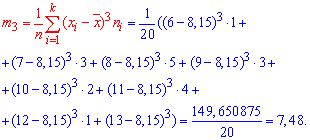
Подставляем в формулу коэффициента асимметрии
![]()
Эксцессом ![]() статистического распределения выборки называется число, которое вычисляют по формуле:
статистического распределения выборки называется число, которое вычисляют по формуле:
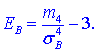
Здесь m4 центральный эмпирический момент 4-го порядка. Находим момент
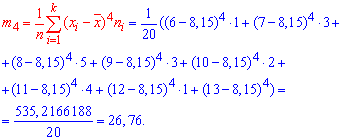
а далее эксцесс![]()
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья – Построение уравнения прямой регрессии Y на X
Представьте, что существует популяция из 10 000 дельфинов, и средний вес дельфина в этой популяции составляет 300 фунтов.
Если мы возьмем простую случайную выборку из 50 дельфинов из этой популяции, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 305 фунтов.
Затем, если мы возьмем еще одну простую случайную выборку из 50 дельфинов, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 295 фунтов.
Каждый раз, когда мы берем простую случайную выборку из 50 дельфинов, вполне вероятно, что средний вес дельфинов в выборке будет близок к среднему значению популяции в 300 фунтов, но не точно 300 фунтам.
Представьте, что мы берем 200 простых случайных выборок из 50 дельфинов из этой популяции и строим гистограмму среднего веса в каждой выборке:
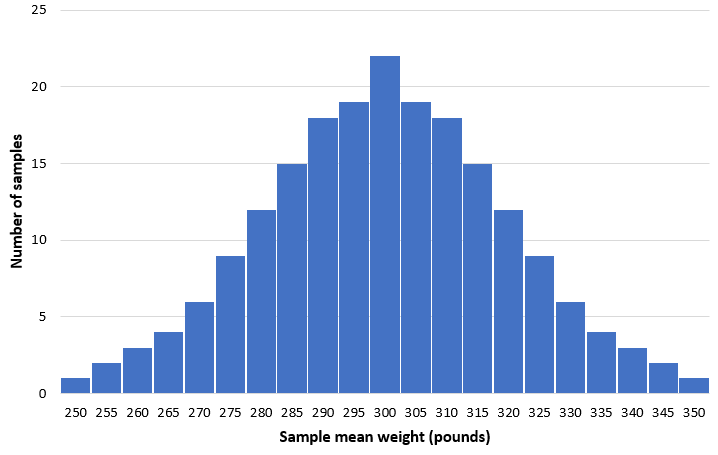
В большинстве образцов средний вес будет близок к 300 фунтам. В редких случаях может случиться так, что мы выберем образец, полный маленьких дельфинов, средний вес которых составляет всего 250 фунтов. Или мы можем случайно выбрать образец, полный крупных дельфинов, средний вес которых составляет 350 фунтов. В целом распределение выборочных средних будет приблизительно нормальным, а центр распределения будет находиться в истинном центре генеральной совокупности.
Это распределение выборочных средних известно как выборочное распределение среднего и обладает следующими свойствами:
м х = м
где μx — выборочное среднее, а μ — среднее значение генеральной совокупности.
σ х = σ/ √n
где σ x — стандартное отклонение выборки, σ — стандартное отклонение генеральной совокупности, а n — размер выборки.
Например, в этой популяции дельфинов мы знаем, что средний вес равен μ = 300. Таким образом, среднее значение выборочного распределения равно μ x = 300 .
Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки равно σ x = 18/√50 = 2,546 .
Выборочное распределение доли
Рассмотрим ту же популяцию из 10 000 дельфинов. Предположим, что 10% дельфинов черные, а остальные серые. Предположим, мы берем простую случайную выборку из 50 дельфинов и обнаруживаем, что 14% дельфинов в этой выборке — черные. Затем мы берем еще одну простую случайную выборку из 50 дельфинов и обнаруживаем, что 8% дельфинов в этой выборке черные.
Представьте, что мы берем 200 простых случайных выборок из 50 дельфинов из этой популяции и строим гистограмму доли черных дельфинов в каждой выборке:
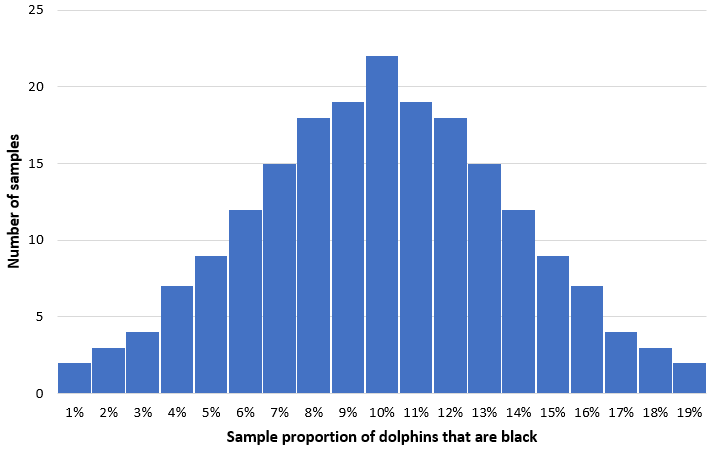
В большинстве выборок доля черных дельфинов будет близка к истинной популяции в 10%. Распределение выборочной доли черных дельфинов будет приблизительно нормальным, а центр распределения будет находиться в истинном центре популяции.
Это распределение выборочных долей известно как выборочное распределение доли и обладает следующими свойствами:
μ р = P
где p — доля выборки, а P — доля совокупности.
σ p = √ (P) (1-P) / n
где P — доля населения, а n — размер выборки.
Например, в этой популяции дельфинов мы знаем, что истинная доля черных дельфинов составляет 10% = 0,1. Таким образом, среднее значение выборочного распределения доли составляет μ p = 0,1 .
Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки равно σ p = √ (P)(1-P) / n = √ (0,1)(1-0,1) / 50 = 0,042 .
Установление нормальности
Чтобы использовать приведенные выше формулы, распределение выборки должно быть нормальным.
Согласно центральной предельной теореме , выборочное распределение среднего значения выборки приблизительно нормально, если размер выборки достаточно велик, даже если распределение генеральной совокупности не является нормальным.В большинстве случаев мы считаем, что размер выборки в 30 или более человек является достаточно большим.
Выборочное распределение доли выборки является приблизительно нормальным, если ожидаемое количество успешных и неудачных попыток равно как минимум 10.
Примеры
Мы можем использовать выборочные распределения для расчета вероятностей.
Пример 1: Определенная машина создает файлы cookie. Распределение веса этих печенек смещено вправо со средним значением 10 унций и стандартным отклонением 2 унции. Если мы возьмем простую случайную выборку из 100 печений, произведенных этой машиной, какова вероятность того, что средний вес печенья в этой выборке будет меньше 9,8 унций?
Шаг 1: Установите нормальность.
Нам нужно убедиться, что выборочное распределение среднего значения выборки является нормальным. Поскольку размер нашей выборки больше или равен 30, в соответствии с центральной предельной теоремой мы можем предположить, что выборочное распределение выборочного среднего является нормальным.
Шаг 2: Найдите среднее значение и стандартное отклонение выборочного распределения.
м х = м
σ х = σ/ √n
мкх = 10 унций
σ x = 2/√100 = 2/10 = 0,2 унции
Шаг 3: Используйте калькулятор площади Z Score, чтобы найти вероятность того, что средний вес печенья в этом образце меньше 9,8 унций.
Введите следующие числа в Калькулятор площади Z Score.Вы можете оставить «Исходный балл 2» пустым, так как в этом примере мы находим только одно число.
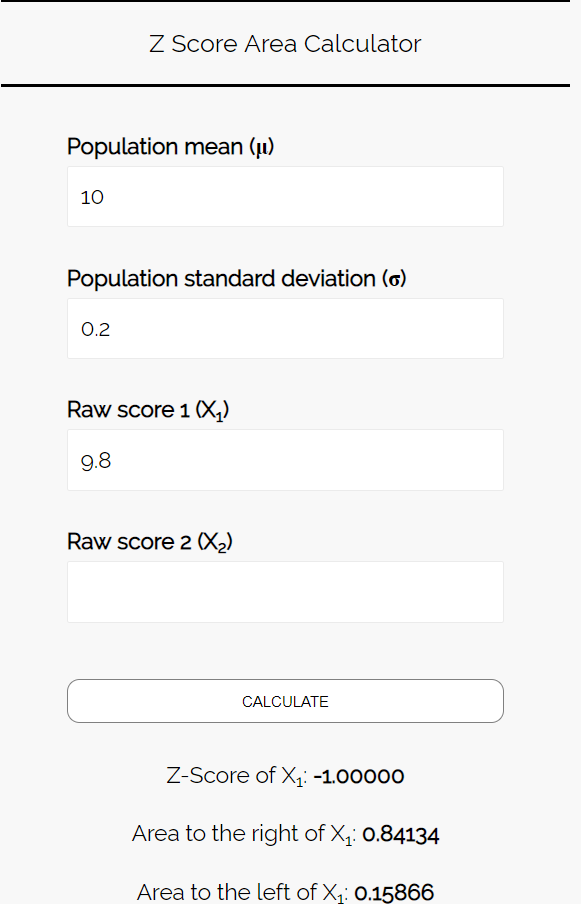
Поскольку мы хотим узнать вероятность того, что средний вес печенья в этой выборке меньше 9,8 унций, нас интересует площадь слева от 9,8. Калькулятор говорит нам, что эта вероятность равна 0,15866 .
Пример 2. Согласно общешкольному исследованию, 87% учащихся в определенной школе предпочитают пиццу мороженому. Предположим, мы берем простую случайную выборку из 200 студентов. Какова вероятность того, что доля студентов, предпочитающих пиццу, меньше 85 %?
Шаг 1: Установите нормальность.
Напомним, что выборочное распределение доли выборки является приблизительно нормальным, если ожидаемое количество «успехов» и «неуспехов» равно как минимум 10.
В этом случае ожидаемое количество студентов, которые предпочтут пиццу, составляет 87% * 200 студентов = 174 студента. Ожидаемое количество студентов, которые не предпочтут пиццу, составляет 13% * 200 студентов = 26 студентов. Поскольку оба эти числа не меньше 10, можно предположить, что выборочное распределение выборочной доли студентов, предпочитающих пиццу, примерно нормальное.
Шаг 2: Найдите среднее значение и стандартное отклонение выборочного распределения.
μ р = P
σ p = √ (P) (1-P) / n
мк р = 0,87
σ p = √ (0,87) (1–0,87) / 200 = 0,024
Шаг 3: Используйте Калькулятор Z Score Area Calculator , чтобы определить вероятность того, что доля учащихся, предпочитающих пиццу, составляет менее 85 %.
Введите следующие числа в Калькулятор площади Z Score.Вы можете оставить «Исходный балл 2» пустым, так как в этом примере мы находим только одно число.
Поскольку мы хотим узнать вероятность того, что доля студентов, предпочитающих пиццу, составляет менее 85 %, нас интересует область слева от 0,85. Калькулятор говорит нам, что эта вероятность равна 0,20233 .
Бонус: видео-объяснение распределений выборки
Ранее мы рассматривали пример анализа, где аналитик оценивал средние планируемые капитальные затраты клиентов на телекоммуникационное оборудование.
Если предположить, что выборка репрезентативна для совокупности, то как аналитик может оценить ошибку выборки при расчете среднего значения по совокупности?
Рассматриваемое как формула, которая использует функцию случайных исходов случайной величины, выборочное среднее само по себе является случайной величиной с распределением вероятностей. Это распределение вероятностей называется выборочным распределением статистики (англ. ‘sampling distribution’).
Иногда возникает путаница, потому что термин «выборочное среднее» также используется в другом смысле. При расчете выборочного среднего для конкретной выборки, мы получаем определенное число, скажем, 8.
Если мы говорим, что «выборочное среднее равно 8», мы используем термин «выборочное среднее» в смысле конкретного исхода выборочного среднего как случайной величины. Число 8 является, конечно же, постоянной величиной и не имеет распределения вероятностей.
В данном обсуждении, мы не рассматриваем «выборочное среднее» как постоянную величину, относящуюся к конкретной выборке.
Для того, чтобы оценить, насколько близко выборочное среднее к среднему по совокупности, аналитик должен понимать распределение выборочного среднего. К счастью, у нас есть для этого инструмент, – центральная предельная теорема, которая помогает нам понять распределение выборочного среднего для многих задач оценивания, с которыми мы сталкиваемся.
Центральная предельная теорема.
Центральная предельная теорема – одна из наиболее практически полезных теорем теории вероятностей. Она имеет важное значение для того, как мы строим доверительные интервалы и проверяем статистические гипотезы.
Формально она формулируется следующим образом:
Для данной генеральной совокупности, описанной любым распределением вероятностей, имеющим среднее ( mu ) и конечную дисперсию ( sigma^2 ), распределение выборочного среднего ( overline X), вычисленное по выборке размера (n) из этой совокупности будет приблизительно нормальным со средним ( mu ) (среднее значение совокупности) и дисперсией ( sigma^2 / n ) (дисперсия совокупности деленная на n), при большом размере выборки (n).
Центральная предельная теорема позволяет сделать довольно точные вероятностные утверждения о среднем значении совокупности на основе выборочного среднего, независимо от размера распределения совокупности (так как оно имеет конечную дисперсию), потому что выборочное среднее приблизительно соответствует нормальному распределению для выборок большого размера.
Тут сразу возникает очевидный вопрос:
«Какой размер выборки можно считать достаточно большим, чтобы мы могли считать, что выборочное среднее соответствует нормальному распределению?»
В целом, если размер выборки ( n ) больше или равен 30, то можно считать, что выборочное среднее приблизительно нормально распределено.
Если генеральная совокупность сильно отличается от нормального распределения, то чтобы получить нормальное распределение, хорошо описывающее распределение выборочного среднего, необходим размер выборки намного больше 30.
Центральная предельная теорема утверждает, что дисперсия распределения выборочного среднего равна ( sigma^2 / n ). Положительный квадратный корень из дисперсии является стандартным отклонением.
Стандартное отклонение выборочной статистики также называют стандартной ошибкой статистики (англ. ‘standard error’).
Стандартная ошибка выборочного среднего является важной величиной в применении центральной предельной теоремы на практике.
Определение стандартной ошибки среднего значения выборки.
Для среднего значения выборки ( overline X) рассчитанного на основе выборки из совокупности со стандартным отклонением ( sigma ), стандартная ошибка среднего значения выборки определяется одним из двух выражений:
( Large dst sigma_{overline X} = {sigma over sqrt n} ) (Формула 1)
когда мы знаем стандартное отклонение совокупности ( sigma ), или
( Large dst s_{overline X} = {s over sqrt n} ) (Формула 2)
когда нам не известно стандартное отклонение совокупности и необходимо использовать стандартное отклонение выборки (s), чтобы оценить его.
Необходимо отметить технический момент: Когда мы делаем выборку размера (n) из конечной совокупности размера (N), мы применяем уменьшающий коэффициент к стандартной ошибке выборочного среднего, который называется поправкой для конечной совокупности (или FPC, от англ. ‘finite population correction factor’).
FPC равна ( [(N – n)/(N – 1)]^{1/2} ).
Таким образом, если (N = 100) и (n = 20), то ( [(100 – 20)/(100 – 1)]^{1/2} = 0.898933 ).
Если мы рассчитали стандартную ошибку равную, скажем, 20, в соответствии с Формулой 1 или Формулой 2, то оценка ошибки с поправкой составляет ( 20(0.898933) = 17.978663 ).
FPC применяется только когда мы делаем выборку из конечной совокупности без замены.
На практике, большинство аналитиков не применяют FPC, если размер выборки (n) слишком мал по сравнению с ( N ) (скажем, менее 5% от (N) ).
Для получения дополнительной информации о поправке для конечной совокупности см. Daniel and Terrell (1995).
На практике, нам почти всегда приходится использовать Формулу 2. Стандартное отклонение выборки (s) можно рассчитать, найдя квадратный корень из дисперсии выборки (s^2), которая рассчитывается следующим образом:
( Large dst
s^2 = {dsum_{i=1}^{n} big ( X_i – overline {X} big )^2 over n-1 } ) (Формула 3)
Мы скоро увидим, как мы можем использовать среднее значение выборки и его стандартную ошибку, чтобы сделать вероятностные утверждения о среднем значении совокупности, используя технику доверительных интервалов.
Но сначала мы проиллюстрируем всю силу центральной предельной теоремы.
Пример (3) применения центральной предельной теоремы.
Примечательно, что выборочное среднее для выборок больших размеров будет распределяться нормально, независимо от распределения генеральной совокупности.
Чтобы проиллюстрировать центральную предельную теорему в действии, мы используем в этом примере явное ненормальное распределение и используем его для создания большого количества случайных выборок размером 100.
Затем мы рассчитываем выборочное среднее для каждой выборки. Частотное распределение рассчитываемых выборочных средних является приближением распределения выборочного среднего для данного размера выборки.
Выглядит ли выборочное распределение как нормальное распределение?
Вернемся к примеру с аналитиком, изучающим планы капитальных затрат клиентов на покупку телекоммуникационного оборудования.
Предположим, что капитальные затраты на оборудование образуют непрерывную равномерную случайную величину с нижним пределом равным $0, и верхним пределом, равным $100. Для краткости, обозначим эту равномерную случайную величину как (0, 100).
Функция вероятности этой непрерывной равномерной случайной величины имеет довольно простую форму, не соответствующую нормальному распределению. Это горизонтальная линия с пересечением на вертикальной оси в точке 1/100. В отличии от нормальной случайной величины, для которой близкие к среднему исходы были бы наиболее вероятны, для равномерной случайной величины все возможные исходы равновероятны.
Чтобы проиллюстрировать силу центральной предельной теоремы, мы проводим моделирование методом Монте-Карло для изучения планируемых капитальных расходов на телекоммуникационное оборудование.
Моделирование методом Монте-Карло предполагает использование компьютера, чтобы смоделировать работу рассматриваемой системы с учетом риска. Составной частью моделирования методом Монте-Карло является генерация большого числа случайных выборок из заданного распределения вероятностей или распределений.
[см. также: CFA – Метод Монте-Карло]
В этом моделировании мы делаем 200 случайных выборок капитальных затрат 100 компаний (200 сгенерированных случайных исходов, каждый из которых состоит из капитальных затрат 100 компаний при (n = 100 )).
В каждом испытании моделирования, 100 значений капитальных затрат генерируются из равномерного распределения (0, 100). Для каждой случайной выборки, мы вычисляем выборочное среднее. Всего мы проводим 200 имитационных испытаний.
Поскольку мы определили распределение, генерирующее выборки, мы знаем, что средние капитальные затраты генеральной совокупности равны ($0 + $100 млн.)/2 = $50 млн.; дисперсия капитальных затрат совокупности равна ( (100 – 0)^2/12 = 833.33 ).
Таким образом, стандартное отклонение составляет $28.87 млн. и стандартная ошибка равна ( 28.87 Big / sqrt {100} = 2.887 ) в соответствии с центральной предельной теоремой.
Если ( a ) является нижним пределом равномерной случайной величины и ( b ) является верхним пределом, то среднее значение случайной величины определяется по формуле ( (a + b)/2 ), а ее дисперсия определяется по формуле ( (b – a)^2/12 ).
В чтении об обычных распределениях вероятности подробно описаны непрерывные равномерные случайные величины.
Результаты этого моделирования методом Монте-Карло приведены в Таблице 2 в виде частотного распределения. Это распределение является рассчитанным выборочным распределением среднего значения.
|
Диапазон выборки |
Абсолютная частота |
|---|---|
|
42.5 (leq overline X <) 44 |
1 |
|
44 (leq overline X <) 45.5 |
6 |
|
45.5 (leq overline X <)47 |
22 |
|
47 (leq overline X <) 48.5 |
39 |
|
48.5 (leq overline X <) 50 |
41 |
|
50 (leq overline X <) 51.5 |
39 |
|
51.5 (leq overline X <) 53 |
23 |
|
53 (leq overline X <) 54.5 |
12 |
|
54.5 (leq overline X <) 56 |
12 |
|
56 (leq overline X <) 57.5 |
5 |
Примечание: ( overline X ) представляет собой средние капитальные затраты для каждой выборки.
Полученное распределение частот можно описать как колоколообразное, с центром, расположенным близко к среднему значению совокупности: 50. Наиболее частый или модальный диапазон, с 41 наблюдениями: от 48.5 до 50.
Общее среднее выборочных средних составляет $49.92, со стандартной ошибкой, равной $2.80. Рассчитанная стандартная ошибка близка к значению 2.887, заданному центральной предельной теоремой.
Расхождение между вычисленными и ожидаемыми значениями среднего и стандартного отклонения, полученными в соответствии с центральной предельной теоремой, является результатом случайности (ошибка выборки).
Таким образом, хотя распределение совокупности очень не нормальное, моделирование показало, что нормальное распределение хорошо описывает рассчитанное распределение выборочного среднего. При этом среднее и стандартная ошибка приближительно равны значениям, предсказанным с помощью центральной предельной теоремы.
Итак, в соответствии с центральной предельной теоремой, когда мы делаем выборку из любого распределения, распределение выборочного среднего будет иметь следующие свойства, если размер нашей выборки достаточно велик:
- Распределение выборочного среднего ( overline X) будет приблизительно соответствовать нормальному распределению.
- Среднее значение распределения ( overline X) будет равно среднему значению генеральной совокупности, из которой сделана выборка.
- Дисперсия распределения ( overline X) будет равна дисперсии совокупности, деленной на размер выборки.
Далее мы обсудим концепции и инструменты, связанные с оценкой параметров совокупности, с особым акцентом на среднее значение совокупности.
Мы фокусируем внимание на среднем значении совокупности, потому что интервальные оценки среднего значения совокупности интересуют финансовых аналитиков, как правило, больше, чем любой другой тип интервальных оценок.
Макеты страниц
Предположим, что мы хотим узнать среднее значение некоторой характеристики генеральной совокупности, например, средний рост десятилетних детей, среднюю заработную плату конторских работников в текстильной промышленности или средний диаметр производимых стальных шайб. Эти генеральные средние могут быть оценены по выборке. Если исходная, или генеральная совокупность нормально распределена, то выборочное распределение выборочных средних также будет иметь нормальное распределение. Даже для ненормального распределения генеральной совокупности, если выборка большая по размеру  , выборочное распределение выборочных средних будет иметь приблизительно нормальное распределение. Этот очень важный вывод основан на центральной предельной теореме.
, выборочное распределение выборочных средних будет иметь приблизительно нормальное распределение. Этот очень важный вывод основан на центральной предельной теореме.
Это позволяет нам использовать здесь все идеи о нормальном распределении, стандартизованных таблицах и  величинах, сформулированных в 2.7.
величинах, сформулированных в 2.7.
По выборочному распределению мы можем вычислить среднее значение всех выборочных средних. Оно представляет собой математическое ожидание выборочной средней:

Если генеральная совокупность является нормальной, то математическое ожидание выборочной средней есть ни что иное как генеральная средняя  т.е.
т.е.

Это равенство справедливо только в том случае, если формирование выборки производилось случайно. В этом случае средняя, полученная по выборочному распределению, называется несмещенной оценкой генеральной средней (средней по совокупности). Пример 4.2 показывает, что это может быть верно и для ненормальной совокупности.
О Пример 4.2. Обратимся к примеру 4.1. Выборочное распределение выборочных средних при  следующее:
следующее:
Таблица 4.3. Вычисление 

Математическое ожидание, полученное по выборочному распределению, составляет:

Данные совокупности: 4, 8, 12, 16, 20 и средняя по совокупности равна:

Следовательно, в нашем примере 
Однако, как уже упоминалось, на практике мы бы не стали действительно строить выборочное распределение на основе многократного проведения выборок из одной и той же совокупности. Следовательно,  не может быть вычислено таким образом. Обычно мы располагаем данными только по одной единственной выборке. Но ввиду того, что нам известно, что
не может быть вычислено таким образом. Обычно мы располагаем данными только по одной единственной выборке. Но ввиду того, что нам известно, что  мы можем использовать единственную выборочную среднюю как несмещенную оценку генеральной средней:
мы можем использовать единственную выборочную среднюю как несмещенную оценку генеральной средней:

где знак обозначает оцениваемую величину.
Надежность оценки будет детально обсуждаться ниже, но она может быть выражена через дисперсию выборочного распределения. Стандартное отклонение выборочного распределения представляет собой стандартную ошибку выборочного распределения, которое обозначается SE (Standard error). Стандартная ошибка выборочных средних обозначается как 


Рис. 4.1. Нормальная генеральная совокупность
Для нормально распределенной генеральной совокупности стандартная ошибка выборочного распределения выборочных средних определяется по формуле:

где а — генеральная дисперсия.
Если генеральная совокупность велика по сравнению с размером выборки (обычно, если это соотношение  , то:
, то:

и стандартная ошибка становится равной:


Рис. 4.2. Выборочное распределение средних х при размере выборок 
Если мы будем изменять размер выборки, то увидим, что средняя выборочного распределения не изменяется, так что  т.е. несмещенная оценка не зависит от размера выборки, тогда как
т.е. несмещенная оценка не зависит от размера выборки, тогда как  уменьшается при возрастании объема выборки (рис. 4.4).
уменьшается при возрастании объема выборки (рис. 4.4).

Рис. 4.3. Нормальная генеральная совокупность индивидуальных значений
При вычислении стандартной ошибки выборочных средних мы предполагаем, что нам известна  (т.е. что известна генеральная дисперсия). Фактически же ее величина неизвестна, и нам необходимо как-то получить оценку генеральной дисперсии по выборке.
(т.е. что известна генеральная дисперсия). Фактически же ее величина неизвестна, и нам необходимо как-то получить оценку генеральной дисперсии по выборке.

Рис. 4.4. Выборочные распределения средних х для выборок объема