Статистические характеристики
Ключевые слова конспекта: статистические характеристики, статистические исследования, выборка, варианта, объем выборки, среднее арифметическое, вариационный ряд, размах ряда, мода выборки, медиана ряда.
Статистические исследования
Для изучения, обработки и анализа количественных данных различных массовых социально-экономических процессов и явлений проводят статистические (от латинского слова status — «состояние, положение вещей») исследования. Уже в древних государствах вели учёт населения, способного платить налоги. С развитием общества потребовались научные методы обработки и анализа самых разнообразных сведений. Так, в XIX в. появилась биологическая статистика, названная биометрикой и изучающая численные характеристики отдельных биологических особей и их популяций. Можно назвать ещё более десятка различных статистик: экономическая, финансовая, налоговая, демографическая, медицинская, метеорологическая и т. д.
Каждое статистическое исследование состоит из сбора и обработки информации. На основе полученных данных составляются различные прогнозы, оценивается их достоверность и т.д. Важной задачей, без которой статистические данные теряют всякий смысл, является обработка полученных данных.
Рассмотрим пример. Учащимся двух седьмых классов был предложен тест по математике, состоящий из 10 заданий. При проверке работ отмечали количество заданий, верно выполненных учащимися. Получили два ряда чисел:
7 «А» класс: 8; 7; 2; 5; 10; 9; 8; 7; 7; 10; 9; 6; 5; 8; 8; 10; 9; 9; 10; 7; 9; 10; 7; 9; 6;
7 «Б» класс: 8; 7; 8; 6; 9; 9; 7; 8; 7; 9; 9; 6; 5; 8; 7; 10; 9; 10; 10; 7; 8; 9; 7; 9; 9.
Ряд данных, полученных в результате статистического исследования, называют выборкой, а каждое число этого ряда — вариантой выборки. Количество чисел в ряду называют объёмом выборки. В нашем примере объёмом выборки является количество учащихся каждого класса, участвовавших в тестировании. В каждом случае объём выборки равен 25.
Имея приведённые выше два ряда данных, трудно сравнить результаты выполнения теста учащимися двух классов. А если рассматривать результаты, которые показали все семиклассники города или целого региона, то информация будет столь громоздкой, что окажется бесполезной. Потому для статистической обработки данных рассматривают различные статистические характеристики.
Среднее арифметическое. Вариационный ряд
Одной из характеристик, широко применяемых в статистических исследованиях, является среднее арифметическое.
✅ Определение. Средним арифметическим ряда данных называется частное суммы всех вариант ряда и количества вариант.
Поскольку количество вариант — это объём выборки, то среднее арифметическое выборки есть частное суммы всех вариант и объёма выборки.
Рассмотрим пример. Найдём средний балл, который получили учащиеся 7 «А» класса при выполнении теста:

Такой подсчёт среднего арифметического выборки не очень удобен. Можно поступать иначе. Перепишем выборку для 7 «А» класса, расположив её варианты так, чтобы каждая следующая была не меньше предыдущей. Получим:
2; 5; 5; 6; 6; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 9; 9; 9; 9; 10; 10; 10; 10; 10.
Такую запись выборки называют упорядоченным рядом данных (или вариационным рядом). Теперь легко видеть, что 2 балла получил один ученик, 5 баллов — два ученика, 6 баллов — два ученика, 7 баллов — пять учеников и т.д. Количество появлений одной и той же варианты в выборке называют частотой этой варианты. Так, например, частота варианты 7 равна 5, частота варианты 10 равна 5. Составим таблицу частот вариант для учащихся 7 «А» класса. В первой строке запишем все возможные количества баллов, которые могли получить учащиеся при выполнении теста, т.е. числа от 0 до 10. Во второй строке запишем соответствующие частоты, т.е. число учащихся, получивших указанное количество баллов.

Проверим, не ошиблись ли мы при подсчёте частот: сумма частот должна быть равна объёму выборки. Действительно, 0 + 0 + 1+ 0 + 0 + 2 + 2 + 5 + 4 + 6 + 5 = 25 (естественно, нули можно не писать). Теперь можно вычислить среднее арифметическое выборки проще:

Заметим, что среднее арифметическое упорядоченного ряда данных и среднее арифметическое выборки — одно и то же число. Составим таблицу частот выборки для 7 «Б» класса.

Заметим, что обычно в таблицу частот не включают варианты, частоты которых равны нулю. В этом случае таблица частот для 7 «Б» класса будет такой:

Найдём объём выборки: 1 + 2 + 6 + 5 + 8 + 3 = 25. Теперь найдём среднее арифметическое:
![]()
Зная средние баллы учащихся 7 «А» и 7 «Б» классов, можно сделать вывод, что учащиеся 7 «Б» в целом выполнили тест лучше, поскольку 8,04 > 7,8.
Составленные таблицы частот позволяют сделать и другие полезные выводы по итогам проведённого тестирования. Например, для первой выборки (результаты учащихся 7 «А» класса) наименьший полученный балл равен 2, наибольший — 10. Результаты всех учащихся класса располагаются между этими числами. Для второй выборки наименьшая варианта равна 5, наибольшая — 10. Это может означать, что 7 «Б» класс по своей математической подготовке является более однородным, чем 7 «А».
Размах ряда. Мода выборки
Ещё одним показателем, который используется при анализе статистических данных, является размах ряда.
✅ Определение. Разность наибольшей и наименьшей вариант выборки называют размахом ряда.
В рассмотренном ранее примере размах первой выборки (или упорядоченного ряда данных) равен 10 — 2 = 8, а второй 10-5 = 5. Размах выборки находят в том случае, когда существенной для исследования является величина разброса данных в ряду. К примеру, в метеорологии важна не только среднесуточная температура, но и численная характеристика колебания температуры воздуха в течение суток, т. е. размах выборки.
Заметим, что на практике при анализе данных, полученных в результате исследования, бывает удобно использовать ещё одну статистическую характеристику — так называемую моду выборки.
✅ Определение. Варианта выборки, имеющая наибольшую частоту, называется модой выборки.
В рассмотренном примере с изучением результатов тестирования, проведённого в двух седьмых классах, модой и первого, и второго ряда является число 9, которое и в первой, и во второй выборке встречается чаще других.
Моду ряда находят тогда, когда нужно выявить типичный для данной выборки показатель. Если, например, изучаются данные о размерах мужских рубашек, проданных в магазине в определённый день, то удобно бывает воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом.
Если в выборке два числа встречаются с одинаковой частотой, превосходящей частоты, с которыми встречаются другие числа, то обе эти варианты являются модой для данного ряда. Так, в ряду 2; 3; 3; 3; 5; 5; 6; 6; 6; 7; 8; 8 две моды — это числа 3 и 6. Может случиться, что в выборке будет более двух мод или не будет моды совсем. Например, ряд 2; 2; 3; 3; 4; 4; 5; 5 не имеет моды.
Медиана ряда
Ещё одной характеристикой, используемой в статистике, является медиана ряда.
Рассмотрим пример. Сотрудники лаборатории приобрели акции одного предприятия. Количество акций, приобретённых сотрудниками, оказалось таким: 2; 3; 5; 6; 8; 9; 51. Нужно оценить среднее количество приобретённых акций.
Данный ряд не имеет моды. Найдём среднее арифметическое ряда:
![]()
Найденное число не отражает реальной ситуации с распределением акций между сотрудниками лаборатории, поскольку оно больше шести из семи вариант ряда. Для оценки средней величины поступим иначе. Составим из полученных данных упорядоченный ряд и найдём варианту, записанную в середине ряда.
2; 3; 5; 6; 8; 9; 51.
Эту варианту называют медианой. Она равна 6. Естественно, найденное значение лишь приближённо характеризует средний показатель ряда, однако эта характеристика ближе к действительности.
Если ряд имеет чётное число вариант, то в качестве медианы рассматривают среднее арифметическое двух средних элементов. Например, медианой ряда 3; 3; 4; 5; 5: 6: 6; 7; 7; 40 является среднее арифметическое чисел 5 и 6, т.е. (5 + 6)/2 = 5,5.
✅ Определение. Если в упорядоченном ряду данных нечётное число вариант, то средняя по счёту варианта называется медианой ряда. Если в упорядоченном ряду чётное число вариант, то среднее арифметическое двух средних по счёту вариант называется медианой ряда.
Медианой произвольной выборки является медиана соответствующего упорядоченного ряда. Заметим, что если упорядоченный ряд данных содержит 2n — 1 вариант (n — натуральное число), то медианой является n-я варианта, а если упорядоченный ряд данных содержит 2n чисел, то медианой является среднее арифметическое n-го и n + 1-го чисел.
Рассмотрим пример. Во время соревнований по стрельбе спортсмен набрал следующее количество очков: 9; 9; 8; 10; 8; 7; 9; 10; 8; 7. Найдём: а) объём выборки; б) среднее арифметическое выборки; в) размах; г) моду ряда; д) медиану выборки.
Для решения задачи запишем упорядоченный ряд данных:
7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
а) Спортсмен сделал 10 выстрелов, значит, объём выборки равен 10.
б) Найдём среднее арифметическое выборки
![]()
в) Размах ряда равен 10 — 7 = 3.
г) У данного ряда две моды: 8 и 9.
д) Найдём медиану выборки. Данный ряд содержит чётное число вариант. Найдём среднее арифметическое двух чисел, записанных в середине ряда: (8 + 9)/2 = 8,5. Медианой выборки является число 8,5.
Это конспект по математике на тему «Статистические характеристики». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Для полноты картины
анализа выборки рассматривают
статистические характеристики
вариационного ряда, которые делятся на
средние характеристики и характеристики
вариации.
4.1. Средние характеристики
К средним
характеристикам относят:
– среднее выборочное;
– моду;
– медиану.
Определение
Выборочной средней
называется среднее арифметическое
значений признака выборочной
совокупности.
В случае, если
ряд дискретный, то:
![]()
,
где
![]()
– значение признака,
![]()
– соответствующая
ему частота.
Вычисления оформим в виде таблицы:
В случае, если
ряд интервальный, то:
![]()
,
где
![]()
– среднее
арифметическое значение интервала,
–
соответствующая ему частота.
Вычисления оформим в виде таблицы:
Определение
Модой называется
варианта с наибольшей частотой.
Если ряд
интервальный,
то выбирают модальный
интервал –
интервал с наибольшей частотой и мода
вычисляется по формуле:

,
где
![]()
–
начало модального интервала,
![]()
– величина интервала,
![]()
–
частота модального интервала,
![]()
– частота интервала,
предшествующего модальному,
![]()
– частота интервала,
следующего за модальным.
Особенности,
которые необходимо учитывать при
вычислении моды в случае дискретного
признака:
1). Если все значения
в выборке встречаются одинаково часто,
принято считать, что группа не имеет
моды.
Пример:
12 12 13 13 14 14 15 15 Моды нет.
2). Если два соседних
значения имеют одинаковую частоту и
они больше частоты любого другого
значения, мода есть среднее этих двух
значений.
Пример:
6 7 7 8 8 8 9 9 9 М0=8,5.
3). Если два несмежных
значения в выборке имеют равные частоты
и они больше частот всех других значений,
то существуют две моды.
Пример: 9
10 10 10 11 11 12 13 13 13 М0=10,
М0=13.
Определение
Медианой называется
такая варианта, при которой одна половина
значений признака меньше ее, а другая
больше.
В случае дискретного
признака
выборку сначала ранжируют,
то есть варианты выборки располагают
в порядке возрастания.
Если число вариант
четное, то:![]()
,
где
![]()
– ранг (порядковый
номер в выборке)
Если число вариант
нечетное, то:
![]()
, где
![]()
.
В случае
непрерывного признака выбирают медианный
интервал –
интервал, в котором накопленная частота
превышает половину объема и медиана
вычисляется по формуле:

,
где
![]()
–
начало интервала, находящегося в середине
вариационного ряда,
– величина интервала,
![]()
–
объем выборки,
![]()
–
накопленная частота интервала,
предшествующего среднему,
![]()
– частота среднего
интервала.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
![]()
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Алгебра и начала математического анализа, 10 класс
Урок №5. Начала статистики.
Перечень вопросов, рассматриваемых в теме
1) статистические характеристики;
2) элементы теории вероятностей;
3) комбинаторные задачи.
Глоссарий по теме
Математическая статистика – наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
Среднее арифметическое n чисел – это частное от деления на n суммы всех этих чисел.
Размах ряда – это разность между наибольшим и наименьшим числом в ряде.
Мода ряда – это число, наиболее часто встречающееся в ряду.
Медиана ряда – среднее число упорядоченного ряда чисел, если ряд нечетный или среднее арифметическое двух средних чисел, если ряд четный.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Процесс познания окружающего мира включает наблюдение и эксперимент. Результаты наблюдений можно представить последовательностью чисел.
Статистика – наука о сборе, обработке и анализе статистической информации. Статистические характеристики – это математические понятия, с помощью которых описываются особенности совокупности данных, полученных с помощью наблюдений.
К статистическим характеристикам относятся: мода, медиана, размах, среднее арифметическое.
Среднее арифметическое n чисел – это частное от деления суммы всех этих чисел на n.
Размах ряда – это разность между наибольшим и наименьшим числом в ряде.
Мода ряда – это число, наиболее часто встречающееся в ряду.
Медиана ряда – среднее число упорядоченного ряда чисел, если ряд нечетный или среднее арифметическое двух средних чисел, если ряд четный
Как же обрабатывает информацию статистика?
1. Данные измерений упорядочивают и группируют.
2. Составляют таблицы распределений данных.
3. По таблицам строят графики распределений.
График распределения частот называют полигоном.
Пусть задача состоит в том, чтобы исследовать некоторый признак. Все множество объектов, входящих в совокупность называют генеральной совокупностью. Часть генеральной совокупности, выбранную случайным образом, называют выборкой.
Числа, которые показывают, сколько раз варианты встречаются в данной совокупности, называют частотами.
Выборка является репрезентативной при обследовании большой группы людей, только так можно сделать верные выводы.
Построение прогнозов и оценок, применение различных методов исследования, достоверность проведенных испытаний и многое другое – вот чем занимается статистика.
Теория вероятностей – раздел математики, который связан с информацией. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных исходов.
Вы знаете, что события бывают: случайные, достоверные, невозможные.
Вероятность случайного события
Р (A) = m / n
где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания.
 – противоположное событие
– противоположное событие

Комбинаторика – раздел математики, который рассматривает различные соединения элементов: перестановки, сочетания, размещения.
Перестановки из n элементов по n:
Pn= n!
Размещения по k элементов из n, отличаются порядком.

Сочетания по k элементов из n, порядок не важен.

Примеры и разбор решения заданий тренировочного модуля
№1. Сколькими способами можно переставить 6 уроков в расписании?
Решение: Это число перестановок равно 6! =120.
Ответ: 120.
№2. 10 человек обменялись визитками. Сколько визиток потребовалось?
Решение: Это размещения: 
Всего потребовалось 90 визиток
Ответ: 90.
№3. 10 человек обменялись рукопожатиями. Сколько рукопожатий было?
Решение: Это сочетания: 
Всего было 45 рукопожатий.
Ответ: 45.
№4. Из 2000 лотерейных билетов 100 – выигрышных. Какова вероятность, что купленный билет выигрышный?
Решение: Р = m/n = 100:2000=0,05 Ответ: 0,05.
Ответ: 0,05.
Урок 1. «Среднее арифметическое, размах и мода»
Тип урока: ознакомление с новым материалом.
Цели:
- обучающая – формирование представления о простейших статистических характеристиках и их использовании при анализе данных, полученных в результате исследования;
- развивающая – знакомство с разделом математики: «статистика и теория вероятностей» и его местом в системе научного познания мира;
- воспитательная – подготовка учащихся к проблемам современной жизни (понимание и интерпретация результатов статистических исследований).
Оборудование: проектор.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
Слышали ли вы когда-нибудь такую песню: «Потому что на десять девчонок по статистике девять ребят»? Как вы думаете, что это значит?
Сегодня мы познакомимся с новой наукой – статистикой. Узнаем, что она изучает и как можно применить те знания, которые вы сейчас получите.
<Презентация 1>
III. Актуализация знаний
– Какое число называют средним арифметическим нескольких чисел?
(Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых).
Задача: дан ряд чисел 5, 6, 8, 12, 15, 4, 17, 8, 10, 15.
- Найдите среднее арифметическое ряда чисел.
- Найдите наибольшее и наименьшее значение ряда чисел, вычислите их разность.
IV. Первичное усвоение, осознание и осмысление нового материала
– Ребята, вы начинаете изучать новый предмет: «Элементы статистики и теории вероятностей».
– Где в реальной повседневной жизни мы сталкиваемся с этими науками?
– Вы что-нибудь слышали об этом разделе математики?
– А разве вам не приходилось подсчитывать среднюю скорость движения, средний бал ученика, класса. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел «Математическая статистика».
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. Вам было дано задание: измерить время, затраченное на выполнение домашнего задания по алгебре.
Мы получили следующие результаты: 27, 25, 26, 25, 40, 38, 38, 25 и т.д.
Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания.
– Что для этого нужно сделать? (сложить все числа и разделить полученную сумму на их количество).
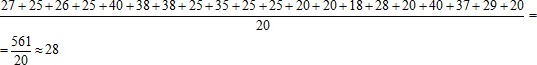
Число 28, полученное в результате, называют средним арифметическим рассматриваемого ряда. Обозначение: ![]() .
.
Мы вычислили, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем 28 минут. Проводя аналогичные наблюдения, можно проследить, какова была средняя затрата времени на выполнение в какой-либо день домашнего задания по алгебре и русскому языку.
Заметим, что иногда вычисление среднего арифметического не дает полезной информации, так как время, затраченное некоторыми учащимися, значительно отличается от среднего арифметического.
Наибольший расход времени равен 40 минут, а наименьший расход времени равен 18 минут. Разность между наибольшим и наименьшим значением называется размахом ряда.
Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду.
-Ребята, нас могут интересовать не только среднее арифметическое и размах, но и другие показатели.
Например, интересно знать, какое число встречается в ряду данных чаще всего.
Таким числом является число 25. Число, наиболее часто встречающееся в данном ряду, называется модой чисел.
Ряд может иметь две моды, а может не иметь моды. Например, 47, 46, 50, 52, 47, 49, 52, 55 – имеет две моды: 47 и 52.
69, 68, 66, 70, 67, 71, 74, 63, 73, 72 – этот ряд не имеет моды.
– Ребята, где еще можно встретить понятие моды ряда чисел?
– Данные о размерах мужских сорочек, проданных в определенный день в универмаге. Здесь мода – размер пользующихся спросом, мода – цены на товар распространенный на рынке и т.п.
V. Закрепление изученного материала
При выставлении оценок учитель также вычисляет среднее арифметическое ваших текущих оценок.
Сейчас вы получите выписку ваших оценок по алгебре за I четверть.
Вы должны вычислить среднее арифметическое, моду и размах.
VI. Подведение итогов урока
Выставление оценок за работу на уроке.
«В среднем в день ребёнок улыбается 400 раз, взрослый — 17. Теперь все улыбнулись, чтобы испортить статистику»
VIII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VII. Постановка домашнего задания п. 9, 168 (а, б), 172, 178
Урок 2. «Медиана как статистическая характеристика»
Тип урока: ознакомление с новым материалом.
Цели:
- обучающая – ввести понятие медианы, организовать деятельность учащихся по закреплению медианы, среднего арифметического, размаха и моды, обеспечить отработку навыка их применения при выполнении различных заданий;
- развивающая – знакомство с разделом математики: «статистика и теория вероятностей» и его местом в системе научного познания мира;
- воспитательная – подготовка учащихся к проблемам современной жизни (понимание и интерпретация результатов статистических исследований).
Оборудование: проектор
Ход урока
I. Организационный момент
II. Проверка домашнего задания
<Приложение 2>
III. Сообщение темы и целей урока
Сегодня на уроке мы повторим алгоритм нахождения среднего арифметического, размаха и моды, и узнаем, как находится еще одна характеристика – медиана.
<Презентация 2>
IV. Актуализация опорных знаний учащихся
1. Фронтальный опрос.
- Что называется средним арифметическим ряда чисел? Может ли среднее арифметическое ряда чисел не совпадать ни с одним из этих чисел?
- Что называется размахом ряда чисел?
- Что называется модой ряда чисел? Любой ли ряд чисел имеет моду? Может ли ряд чисел иметь более одной моды? Может ли мода ряда чисел не совпадать ни с одним из этих чисел?
2. Устный счет.
а) Дан ряд чисел: 3, 5, 1, 7, 9. Найти среднее арифметическое, размах и моду.
б) Дан ряд чисел: 1, 2, 2, 5, 5. Найти среднее арифметическое, размах и моду.
V. Первичное усвоение, осознание и осмысление нового материала
Задача. В небольшой фирме 10 сотрудников: 7 рабочих, мастер, бухгалтер, директор. Зарплата у рабочих: 2000, у мастера 4000, у бухгалтера 16000, у директора 40000. Найдите чему будет равна средняя зарплата на этом предприятии?
Решение:
![]()
Но достаточно ли этой характеристики работнику, который устраивается работать рабочим? (Нет)
В этом случае используют другую статистическую характеристику – медиану.
Запишем алгоритм нахождения медианы набора чисел:
- Упорядочить числовой набор.
- Одновременно зачеркиваем “самое большое” и “самое маленькое” числа данного набора чисел до тех пор, пока не останется одно число или два числа.
- Если осталось одно число, то оно и есть медиана.
- Если осталось два числа, то медианой будет среднее арифметическое двух оставшихся чисел.
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
VI. Закрепление изученного материала
Задача 2. В таблице приведена информация о длине основных рек, протекающих по территории округа Домодедово Московской области.
| Река | Длина, км |
| Пахра | 900 |
| Рожайка | 51 |
| Битца | 24 |
| Гнилуша | 31 |
| Северка | 98 |
| Конопелька | 13 |
а) Найдите среднюю длину рек (среднее арифметическое);
б) Найдите длину рек в среднем (медиану данных);
в) По вашему мнению, какая из этих характеристик – среднее арифметическое или медиана – лучше описывает длину рек, протекающих в Домодедовском районе? Ответ объясните.
Ответ: а) 186 км, б) 41 км, в) медиана, т.к. данные содержат значения сильно отличающиеся от всех прочих.
Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях одна из характеристик может не иметь никакого содержательного смысла.
VI. Подведение итогов урока
У статистиков есть шутка: средняя глубина озера 0,5 м, а корова все-таки утонула. Как вы понимаете эту фразу?
Выставление оценок за работу на уроке.
VIII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VII. Постановка домашнего задания п.10, 187, 190, 193
Урок 3. «Статистические характеристики»
Тип урока: закрепление изученного.
Цели:
- обучающая – закрепить полученные знания и умения, применять статистические характеристики при решении простейших задач;
- развивающая – развитие математически грамотной речи, логического мышления;
- воспитательная – подготовка учащихся к проблемам современной жизни, воспитание познавательной активности, культуры диалога.
Оборудование: карточки для выполнения проверочной работы.
Ход урока
I. Организационный момент
II. Проверка домашнего задания, уточнение направлений актуализации материала
<Приложение 2>
III. Сообщение темы, цели и задач урока, мотивация учения
Сегодня на уроке мы продолжим находить основные статистические характеристики числовых рядов.
IV. Воспроизведение изученного и их первичное применение в новых или измененных условиях с целью формирования умений
1. Фронтальный опрос
- Что такое статистика?
- Какие статистические характеристики вы знаете?
- Что называется средним арифметическим ряда чисел?
- Что называется размахом ряда чисел?
- Что называется модой ряда чисел?
- Любой ли ряд имеет моду?
- Может ли ряд иметь более одной моды?
- Может ли мода ряда чисел не совпадать ни с одним из этих чисел?
- Что называется медианой ряда чисел?
- Какой ряд называется упорядоченным рядом чисел?
2. Решение задач
В таблице приведены расходы учащегося 7 класса за 4 дня:
| День | Понедельник | Вторник | Среда | Четверг |
| Расходы | 100 | 75 | 50 | 75 |
Определить какая статистическая характеристика находится в каждом задании:
а) 100+75+50+75=30;
300:4=75;
___=75 р.б) 50, 75, 75, 100;
(75+75):2 = 75;
___=75 р.в) 100, 75, 50, 75;
___=75 р.г) 100-50=50;
___=50 р.
3. Решение заданий повышенной сложности
<Приложение 3>
V. Проверочная работа
<Приложение 4>
Выдаются карточки с заданием. Эти карточки подписываются учащимися. Задания выполняются на этих карточках в течение 3-5 минут.
Ребята меняются карточками. И по готовым ответам на доске проверяют работы друг друга и выставляют отметки согласно предложенным критериям.
Оценка: «5» – всё верно; «4» – 3 задания выполнены верно; «3» – 2 задания выполнены верно; «2» – выполнено верно менее двух зданий.
Работы сдаются учителю для просмотра и анализа усвоения материала.
VI. Подведение итогов урока
Выставление оценок за урок.
VII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
VIII. Постановка домашнего задания №182, №183, №193
Провести сбор информации на тему: «Размер обуви учеников 7 класса», «Рост учеников 7 класса», «Количество детей в семье учеников 7 класса» (в трех экземплярах) <Приложение 5>
Урок 4. «Статистические характеристики нашего класса»
Тип урока: обобщения и систематизации знаний.
Цели:
- обучающая – повторение и закрепление пройденного материала, введение понятия статистического исследования, продемонстрировать удобные способы упорядочивания и систематизации больших объёмов информации;
- развивающая – развитие математически грамотной речи, логического мышления;
- воспитательная – воспитание познавательной активности, культуры диалога.
Оборудование: таблицы для заполнения данных.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
– На перемене я собрала ответы на все ваши вопросы. Все готовы приступить к групповому исследованию. Начинаем заключительный урок по теме “Статистические характеристики”.
III. Воспроизведение и коррекция опорных знаний
- Что такое статистика?
- Какие статистические характеристики вы знаете?
IV. Обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий
Сегодня на уроке мы проведем с вами статистическое исследование.
Запишем основные этапы статистического исследования:
- Сбор данных.
- Систематизация данных – представление данные в табличном виде.
- Анализ данных – нахождение статистических характеристик, выводы.
Рассмотрим следующую задачу:
В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
| Цена (руб.) | 500 | 1200 | 1500 | 1800 | 2000 | 2500 |
| Количество | 8 | 9 | 14 | 15 | 3 | 1 |
Первый и второй этап статистического исследования уже пройдены: данные собраны и систематизированы. Осталось произвести анализ данных.
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы:
- Из данных ценовых категорий, обувь за какую цену не следует продавать магазину?
- Обувь, по какой цене следует распространять?
- К какой цене лучше стремиться?
По каким параметрам еще можно провести статистические исследования в обувном магазине?
V. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний
Проведем собственное статистическое исследование. У вас было домашнее задание: принести данные о своем росте, размере обуви и количестве детей в семье.
Сейчас каждый ряд получит свое задание <Приложение 5>:
- Провести статистическое исследование роста учащихся вашего класса.
- Провести статистическое исследование размера обуви.
- Провести статистическое исследование количества детей в семье.
Так как статистическое исследование состоит из трех этапов, а первый этап – сбор данных мы уже провели, то вы можете переходить ко второму этапу – систематизации данных. Для этого данные занесите в таблицы.
После того как вы провели систематизацию данных, можно переходить к следующему этапу – анализу данных. Найдите статистические характеристики: среднее арифметическую, моду, медиану и размах ряда. Сделайте выводы.
VI. Подведение итогов урока
Вы все отлично справились с заданием. Выставление оценок за работу на уроке.
VII. Постановка домашнего задания
Провести исследование на тему: «Рост учащихся 8 класса».
VII. Рефлексия
Раздать карточки для рефлексии.
<Приложение 1>
