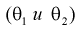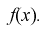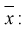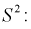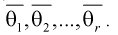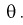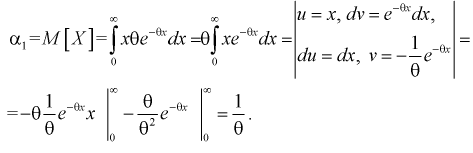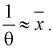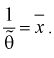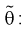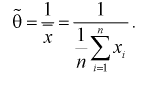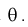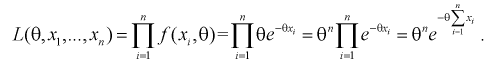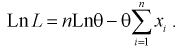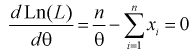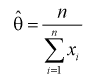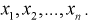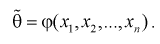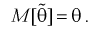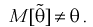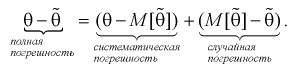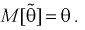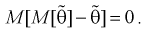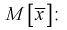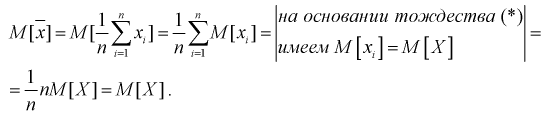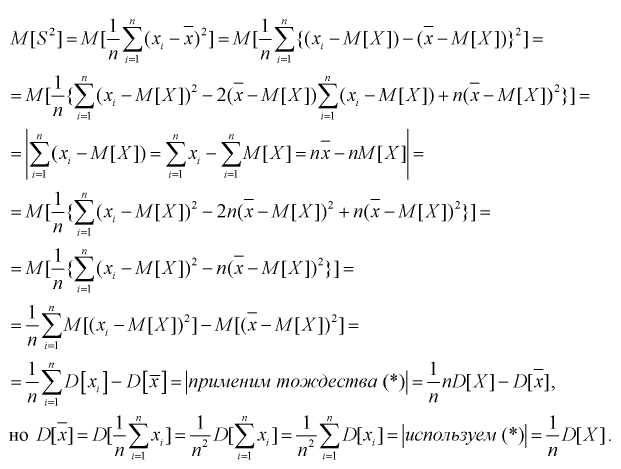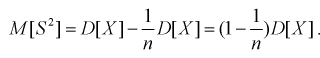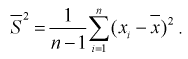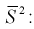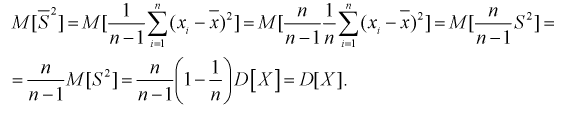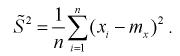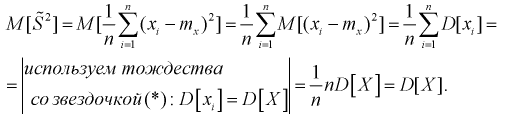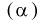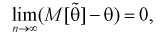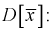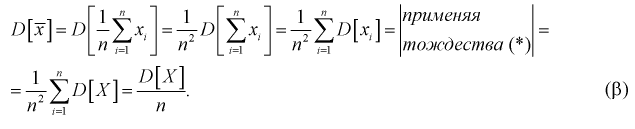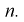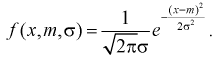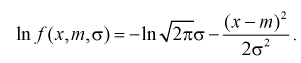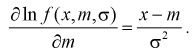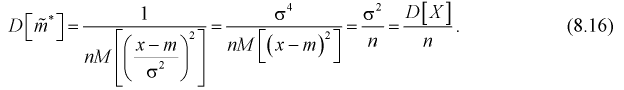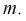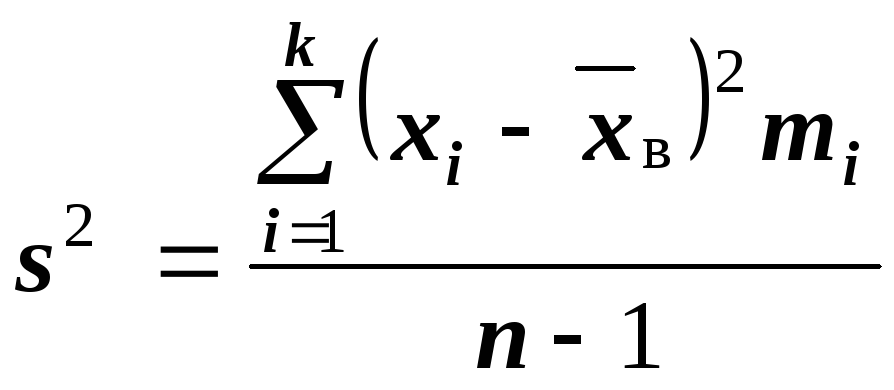Как найти статистическую оценку

Содержание:

1. Точечные статистические оценки параметров генеральной совокупности 
2. Методы определения точечных статистических оценок
3. Законы распределения вероятностей для 
4. Интервальные статистические оценки для параметров генеральной совокупности 
5. Построение доверчивого интервала для  при известном значении  с заданной надежностью  
6. Построение доверительного интервала для  при неизвестном значении  из заданной надежности 
7. Построение доверительных интервалов с заданной надежностью  для 
8. Построение доверительного интервала для  генеральной совокупности с заданной надежностью 
9. Построение доверительного интервала для  с помощью неравенства Чебишова с заданной надежностью 

Информация, которую получили на основе обработки выборки про признак генеральной совокупности, всегда содержит определенные погрешности, поскольку выборка содержит только незначительную часть от нее  то есть объем выборки значительно меньше объема генеральной совокупности. 

Потому, следует организовать выборку так, чтобы эта информация была более полной (выборка может быть репрезентабельной) и обеспечивала с наибольшей степенью доверия о параметрах генеральной совокупности ил закон распределение ее признака. 

Параметры генеральной совокупности  являются величинами постоянными, но их числовые значения неизвестные. Эти параметры оцениваются параметрами выборки:   которые получаются при обработке выборки. Они являются величинами непредсказуемыми, то есть случайными. Схематично это можно показать так (рис. 115). 

Тут через   обозначен оценочный параметр генеральной совокупности, а через    – его статистическую оценку, Которую называют еще статистикой. При этом   а  – случайная величина, что имеет полный закон распределения вероятностей. заметим, что для реализации выборки каждую ее варианту рассматривают как случайную величину, что имеет закон распределения вероятностей признака генеральной совокупности с соответственными числовыми характеристиками: 

Точечные статистические оценки параметров генеральной совокупности 

Статистическая оценка  , которая обозначается одном числом, называется точечной. Возьмем во внимание, что  является случайной величиной, точечная статистическая оценка может быть смещенной или несмещенной: когда математическое надежда этой оценки точно равны оценочному параметру  а именно: 

то  называется несмещенной; в противоположном случае, то есть когда 

 

точечная статистическая оценка     называется смещенной относительно параметра генеральной совокупности 

 Разница 

называется смещением статистической оценки 

Оценочный параметр может иметь несколько точечных несмещенных статистических оценок, что можно изобразить так (рис. 116):

Например, пусть  которая имеет две несмещенные точечные статистические оценки –   и  Тогда плотность вероятностей для    имеют такой вид (рис. 117): 

Из графиков плотности видим, что оценка   сравнено с оценкой  имеет то преимущество, что около параметра   Отсюда получается,  что оценка  чаще получает значение в этой области, чем оценка 

Но на “хвостах” распределений имеет другую картину: большие отклонения от  будут наблюдаться для статистической оценки , чаще, чем для  Потому, сравнивая дисперсии статистических  как меру рассеивания, видим, что   имеет меньшую дисперсию, чем оценка . 

Точечная статистическая оценка называется эффективной, когда при заданном объеме выборки она имеет минимальную дисперсию. Следует, оценка  будет несмещенной и эффективной. 

Точечная статистическая оценка называется основой, если в случае неограниченного увеличения объема выборки  приближается к оценке параметра , а именно: 

Методы определения точечных статистических оценок

Существует три метода определения точечных статистических оценок для параметров генеральной совокупности. 

Метод аналогий. Этот метод основывается на том, что для параметров генеральной совокупности выбирают такие же параметры выборки, то есть для оценки  выбирают аналогичные статистики – 

Метод наименьших квадратов. Согласно с этим методом статистические оценки обозначаются с условием минимизации суммы квадратов отклонений вариант выборки от статистической оценки . 

Итак, используя метод наименьших квадратов, можно, например, обозначить статистическую оценку для  Для этого воспользуемся функцией   Используя условие экстремума, получим: 

Отсюда, для  точечной статистической оценкой будет  – выборочная средняя. 

Метод максимальной правдоподобности. Этот метод занимает центральное место в теории статистической оценки параметров  На него в свое время обратил внимание К. Гаусс, а  разработал его Р. Фишер. Этот метод рассмотрим подробнее. 

Пусть признак генеральной совокупности   обозначается только одном параметром   и имеет плотность вероятности   В случае реализации выборки с вариантами   плотность вероятности выборки будет такой: 

В этом варианте рассматриваются как независимые случайные величины, которые имеют один и тот же закон распределения, что ее признак генеральной совокупности . 

Суть этого метода состоит в том, что фиксируя значение вариант ,  обозначают такие значение параметра  , при котором функция   максимизуется. Она называется функцией максимальной правдоподобности и обозначается так: 

Например, когда признак генеральной совокупности   имеет нормальный закон распределения, то функция максимальной правдоподобности приобретет такой вид: 

При этом статистические оценки   выбирают и ее значения, по которых заданная выборка будет верной, то есть функция   достигает максимума. 

На практике удобно от функции  перейти к ее логарифму, а именно: 

согласно с необходимым условием экстремума для этой функции получим: 

Из первого уравнения системы    получим: 

из уравнение системы   получим: 

Следует, для  точечной функции статистической оценкой будет    для  

Свойства  Исправленная дисперсия, исправленное среднее квадратичное отклонение. Точечной несмещенной статистической оценкой для   будет 

И на самом деле, 

  учитывая то. что  

Следует, 

Проверим на несмещенность статистической оценки 

Таким образом, получим 

Следует,  будет точечной смещенной статистической оценкой для ,  где   – коэффициент смещения, который уменьшается с увеличением объема выборки  

Когда  умножить на   то получим 

Тогда 

Следует,  будут точеной несмещенной статистической оценкой для  Ее называли исправленной дисперсией и обозначили через  

Отсюда точечной несмещенной статистической оценкой для  будет исправленная дисперсия    или 

Величину 

называют исправленным средним квадратичным отклонением.

Исправленное среднее квадратичное отклонение, следует подчеркнуть, будет смещенной точечной статистической оценкой для      поскольку 

где  является ступенью свободы;

  – коэффициенты смещения. 

Пример. 200 однотипных деталей были отданы на шлифование. Результаты измерения приведены как дискретное статистическое распределение, подан в табличной форме: 

Найти точечные смещенные статистические оценки для  

Решение. Поскольку точечной несмещенной оценки для   будет   то вычислим 

Для обозначение точечной несмещенной статистической оценки для   вычислим 

тогда точечная несмещенная статистическая оценка для  равно: 

Пример. Граничная нагрузка на стальной болт   что измерялась в лабораторных условий, задано как интервальное статистическое распределение: 

Обозначить точечные несмещенные статистические оценки для 

Решение. Для обозначения точечных несмещенных статистических распределений к дискретному, который приобретает такой вид: 

Вычислим 

Следует, точечная несмещенная статистическая оценка для  

Для обозначения   вычислим 

Отсюда точечная несмещенная статистическая оценка для   будет 

Законы распределения вероятностей для 

Как уже обозначалось, числовые характеристики выборки являются случайными величинами, что имеют определенные законы распределения вероятностей. Так,   (выборочная средняя) на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) имеем нормальный закон распределения с числовыми характеристиками 

следует, случайная величина   имеет закон распределения 

Чтобы обозначить закон распределения для  необходимо выявить связь между  и распределением . 

Пусть признак генеральной совокупности    имеет нормальный закон распределения . При реализации выборки каждую из вариант   рассматривают как случайную величину. то также имеет закон распределения . При этом вариант выборки является независимым, то есть   а случайная величина   соответственно имеет закон распределения 

Рассмотрим случай,  когда варианты выборки имеют частоты  тогда 

 

Перейдем от случайных величин  к случайным величинам  которые линейно выражаются через  а именно:  

Поскольку случайные величины    будут линейными комбинациями случайных величин  то  тоже имеют нормальный закон распределения с числовыми характеристиками: 

Следует, случайные величины  имеют закон распределения 

Построим матрицу   элементы которой будут коэффициенты при    в линейных зависимостях для 

Транспортируем матрицу  получим:

Если перемножить матрицы  и  то получим: 

где   будет единичная матрица. 

Следует, случайные величины  обозначены ортогональными преобразованиями случайных величин   В векторной – матричной форме это можно записать так: 

Из курса алгебры известно, что во время ортогональных преобразований вектора сохраняется его длина, то есть 

Тогда из формулы для   получим: 

Поскольку   далее вычислим: 

Следует, получим 

Когда поделим левую и правую часть    на  то получим, 

Поскольку  имеет закон распределения   то  получим закон распределения  то есть нормированный нормальный закон. 

То случайная величина 

получим распределение   из   ступенями свободы. 

Отсюда получается, что случайная величина   получим распределение  из   ступенями свободы. 

Таким образом, приведена: случайная величина  тут символ  нужно читать “распределена как”; 

случайная величина 

случайная величина 

Интервальные статистические оценки для параметров генеральной совокупности 

Точечные статистические оценки   являются случайными величинами, а потому приближенная замена   на  часто приводит к существенным погрешностям, особенно когда объем выборки не большой. В этом случае используют интервальные статистические оценки.

Статистическая оценка, что обозначается двумя числами, концами интервалов, называется интервальной. 

Разница между статистической оценкой  и ее оценкой параметром   взята с абсолютным значением, называется точностью оценки, а именно: 

где   является точностью оценки. 

Поскольку  является случайной величиной, то и  будет случайной, потому неравенство   справедливо с определенной вероятностью. 

Вероятность, с которой берется неравенство , то есть 

называется надежностью

Равенство  можно записать так:

Интервал  что покрывает оценочный параметр  генеральной совокупности с заданной надежностью  называют доверчивым. 

Построение доверчивого интервала для  при известном значении  с заданной надежностью  

Пусть признак  генеральной совокупностью имеет нормальный закон распределению. Построим доверительный интервал для  зная числовое значение среднего квадратичному отклонению генеральной совокупности     с заданной надежностью  Поскольку  как точечная несмещенная статистическая оценка для   имеет нормальный закон распределения с числовыми характеристиками    то воспользовавшись  получим 

Случайная величина  имеет нормальный закон распределения с числовыми характеристиками 

Потому   будет нормированный нормальный закон распределения 

Отсюда равенство   можно записать, обозначив  так; 

или 

Согласно с формулой нормированного нормального закона 

для  она получает такой вид: 

Из равенства   находим аргументы   а именно: 

Аргумент   находим значение функции Лапласа, которая равна   по таблице (дополнение 2). 

Следует, доверительный интервал равен: 

что можно изобразить условно на рисунке 118. 

Величина    называется точностью оценки, или погрешностью выборки. 

Пример. Измеряя 40 случайно отобранных после изготовления деталей, нашли выборку средней, что равна 15 см. Из надежности   построить доверительный интервал для средней величины всей партии деталей, если генеральная дисперсия равна 

 Решение. Для построенного доверчивого интервала необходимо найти: 

Из условия задачи имеем:   Величина  вычисляется из уравнения

 {с таблицей значения функции Лапласа}. 

Найдем числовые значения концов доверчивого интервала: 

Таким образом, получим: 

Следует, с надежностью   (99%  гарантии) оценочный параметр   пребывает в середина интервала 

Пример. Имеем такие данные про размеры основных фондов (в млн руб.) на 30-ти случайно выбранных предприятий: 

построить интервальное статистическое распределение с длиной шага  млн рублей. 

С надежностью  найти доверительный интеграл для  если  млн рублей. 

Решение. Интервальное статистическое распределение будет таким: 

Для обозначение  необходимо построить дискретное статистическое распределение, что имеет такой вид: 

Тогда 

  млн рублей. 

Для построения доверительного интервала с заданной надежностью  необходимо найти 

Вычислим концы интервала: 

 млн руб.

млн руб.

Следует, доверительный интервал для  будет 

Пример. Какое значение может получит надежность оценки  чтобы за объем выборки  погрешность ее не превышала  при 

Решение. Обозначим погрешность выборки 

Далее получим: 

как видим, надежность мала. 

Пример. Обозначить объем выборки  по которому погрешность  гарантируется с вероятностью   если 

 Решение. По условию задачи  Поскольку   то получим:  Величину   находим из равенства  Тогда 

Построение доверительного интервала для  при неизвестном значении  из заданной надежности 

Для малых выборок, с какими сталкиваемся, исследуя разные признаки в техники или сельском хозяйстве, для оценки   при неизвестном значении  невозможно воспользоваться нормальным законом распределения. Потому для построения доверительного интервала используется случайная величина. 

что имеет распределение Стьюдента с  ступенями свободы. 

Тогда  получает вид: 

поскольку  для распределения Стьюдента является функцией четной. 

Вычислив по данному статистическому распределению   и обозначив по таблице распределения Стьюдента значения  построим доверительный интервал 

Тут  вычислим по заданной надежностью   и числом степеней свободы   по таблице (дополнение 3).

Пример. Случайно выбранная партия из двадцати примеров была испытана относительно срока безотказной работы каждого из них  Результаты испытаний приведено в виде дискретного статистического распределения: 

С надежностью  построить доверительный интервал для  (среднего времени безотказной работы прибора.)

Решение. Для построения доверительного интеграла необходимо найти среднее выборочное и исправленное среднее квадратичное отклонение. 

Вычислим 

следует, получили  часов. 

Обозначим 

следует, 

Исправленное среднее квадратичное отклонение равно: 

 часов.

По таблице значений  (дополнение 3) распределение Стьюдента по заданной надежностью   и числом ступеней свободы  находим значение 

Вычислим концы доверительного интервала: 

 час.

 час. 

Следует, с надежностью  можно утверждать, что   будет содержится в интервале 

При больших объемах выборки, а именно:  на основании центральной граничной теоремы теории вероятностей (теоремы Ляпунова) распределение Стьюдента приближается к нормальному закону. В этом случае  находиться по таблице значений функции Лапласа. 

Пример. В таблице приведены отклонения диаметров валиков, изготовленных на станке, от номинального размера: 

с надежностью  построить доверительный интервал для 

Решение. Для постройки доверительного интервала необходимо найти 

Для этого от интегрального статистического распределения, приведенного в условии задачи, необходимо перейти к дискретному, а именно: 

Вычислим 

 поскольку 

Следует, 

Обозначим 

Вычислим исправленное среднее квадратичное отклонение 

Учитывая  на большой  объем выборки можно считать, что распределение Стьюдента близкий к нормальному закону. Тогда по таблице значения функции Лапласа

Вычислим концы интервалов: 

Итак, доверчивый интервал для среднего значения отклонений будет таким: 

Отсюда с  надежностью  можно утверждать, что

Построение доверительных интервалов с заданной надежностью  для 

В случае, если признак  имеем нормальный закон распределения, для построения доверительного интервала с заданной надежностью  для   используем случайную величину 

что имеет распределение  из  ступенями свободы. 

Поскольку случайные действия 

 и 

являются равновероятными, то есть их вероятности равны  получим: 

Подставляя в   получим 

Следует, доверительный интервал для  получит вид: 

Тогда доверительный интервал для  получается из  и будет таким: 

Значения  находятся по таблице (дополнение 4) согласно с равенствами: 

где 

Пример. Проверена  партия однотипных телевизоров  на чувствительность к видео-программ   данные проверки приведены как дискретное статистическое распределение: 

С надежностью  построить доверительные интервалы для 

Решение. Для построении доверительных интервалов  необходимо найти значения 

Вычислим значения 

 так как 

Вычислим 

Следует 

Исправленная дисперсия и исправленное среднее квадратичное отклонение равны:  

Поскольку  то согласно с  находим значения  а именно: 

По таблице (дополнение 4) находим: 

вычислим концы доверительного интервала для 

Следует, доверительный интеграл для  будет таким: 

Доверительный интервал для  станет

Доверительный интервал для  можно построить с заданной надежностью  взяв распределение 

Поскольку 

то равенство  можно записать так: 

или 

Обозначив  получим

чтобы найти  возьмем случайную величину 

что имеет распределение 

Учитывая то, что события

 и 

при  является равновероятными, получим: 

Если умножить все члены двойного неравенства  на  то получим: 

Отсюда получим: 

Из уравнения  по заданной надежностью  и объемом выборки  находим по таблице (дополнение 5) значение величины 

Доверительный интервал будет таким: 

Пример. С надежностью  построить доверительный интервал вычислим значения  по таблице (дополнение 5). 

Обозначим концы интервала: 

Следует, доверительный интервал для  с надежностью  будет такой 

Построение доверительного интервала для  генеральной совокупности с заданной надежностью 

Как величина, полученная по результатам выборки,  является случайной и представляет собой точечную несмещенную статистическую оценку для 

Исправленное среднее квадратичное отклонение для  

Для построения доверительного интервала для  используется случайная величина

что имеет нормированный нормальный закон распределения  

Воспользовавшись  получим 

Следует. доверительный интервал для будет таким: 

где  находим из равенства 

по таблице значений функции Лапласа. 

Пример. Случайно выбранных студентов из потока университета были подвергнуты тестированию по математике и химии. Результаты этих тестирования преподнесено статистическим распределением, где  – оценки по математике,  – по химии. Ответы оценивались по десятибалльной системе: 

Необходимо: 

1) с надежностью  построить доверительный интервал для   если 

2) с надежностью  построить доверительный интервал для 

Решение. Вычислим основные числовые характеристики признак  и  а также  Поскольку  получим: 

1. Построим доверительный интервал с надежностью  для  если 

нам известные значения  Значения   вычисляем из уравнения  

где  находим по таблице значений функции Лапласа. 

Обозначим концы интервала: 

Следует, доверительный интервал для  будет таким: 

2. Построим доверительный интервал с надежностью  для 

Поскольку    нам не известно, то доверительный интервал в этом случае обозначается так: 

На известное значение  находим по таблице распределения Стьюдента (дополнение 3),

Вычислим концы доверительного интервала: 

Таким образом, доверительный интервал для  будет в таких границах: 

Доверительный интеграл с надежностью  для  будет таким: 

Нам известно значение  Учитывая, что  найдем по таблице (дополнение 5) значения 

Обозначим концы доверительного интервала: 

Следует, доверительный интервал для  подается таким неравенством: 

Доверительный интервал для  с заданной надежностью  будет таким: 

Нам известны значения  обозначаем по таблице значений функции Лапласа  где 

Обозначим концы доверительного интервала: 

таким образом, доверительный интервал для  будет в таких границах: 

Построение доверительного интервала для  с помощью неравенства Чебишова с заданной надежностью 

В случае, если отсутствует информация про закон распределения признака генеральной совокупности   оценка вероятностей события  где  и построение доверительного интервала для  с заданной надежностью  выполняется с использованием неравенства Чебишова по условию, что известно значение   а именно: 

Из  обозначаем величину 

Доверительный интервал дается таким неравенством: 

Когда  неизвестно, используем исправленную дисперсию  и доверительный интервал приобретает такой вид: 

Пример. Полученные данные с 100 наугад выбранных предприятий относительно возрастания выработки на одного работника  которые имеют такой интервальное статистическое распределение: 

Воспользовавшись неравенством Чебишова, построить доверительный интервал для  если известно значение  с надежностью 

Решение. Для построения доверительного интервала с помощью неравенства Чебишова необходимо вычислить  Чтобы обозначить  перейдем от интервального к дискретному статистическому распределению, а именно: 

Тогда получим: 

Воспользовавшись  вычислим 

таким образом, доверительный интервал для  преподноситься такими неравенствами: 

или 

Пример. Заданы размеры основных фондов  на 30- ти предприятий дискретным статистическим распределением: 

Воспользовавшись неравенством Чебишова с надежностью  построить доверительный интервал для 

Решение. Для постройки доверительного интервала для    с помощью неравенства Чебишова необходимо вычислить 

 млн руб. 

Следует,  млн рублей. 

  млн рублей.

Обозначить концы доверительного интервала: 

 млн рублей

н рублей

Итак, доверительный интервал для  подается неравенствами

Содержание:

Оценки и методы их получения:

Приближенные значения параметров, входящих в законы распределения, определяемые каким-либо способом по выборкам, называются оценками или статистиками. Оценки бывают точечными и интервальными. Точечные оцен­ки представляются одним числом, интервальные – двумя числами

Метод моментов

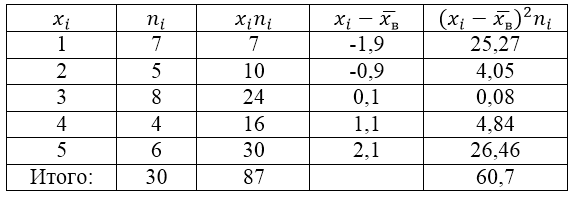
Пусть генеральная случайная величина X имеет плотность распределения

                                   (8.1)

                              (8.2)

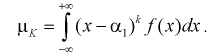
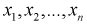
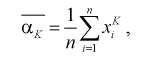
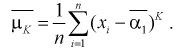
По выборке  определяем выборочные начальные и центральные моменты:

                (8.3)

           (8.4 )

Метод моментов состоит в том, что генеральные моменты (8.1, 8.2), в которые входят оцениваемые параметры, приблизительно приравниваются к со­ответствующим выборочным моментам (8.3), (8.4). Составляется система уравнений:
                             (8.5)
                                (8.6)

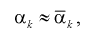
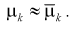
Решая систему (8.5), (8.6), находим оцениваемые параметры.
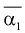
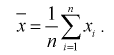
Особо важную роль играет  – выборочный начальный момент 1-го по­ рядка, он называется выборочным средним и обозначается

    (8.7)

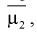
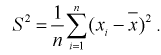
Следующим по важности выборочным моментом является выборочный центральный момент 2-го порядка  который называется выборочной дисперсией и обозначается
                                    (8.8)

Наиболее часто используются две формулы метода моментов.
                                        (8.9)

         (8.10)

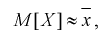
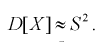
Сформулируем метод моментов в общем виде.
 

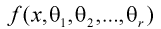
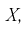
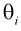
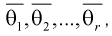
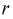
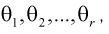
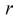
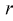
Пусть плотность распределения случайной величины  где  – неизвестные параметры. Чтобы найти оценки  выражаем первые  начальных или центральных моментов случайной величины X через параметры  затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из  уравнений с неизвестными, откуда и получаем
 

Пример:

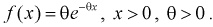
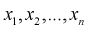
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью  По выборке  методом моментов найти оценку параметра

 1. Определяем 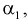 используя (8.1): 

2. По (8.3) или (8.7) находим выборочный начальный момент 1-го поряд­ка или 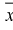 и составляем выражение вида (8.5) или (8.9):

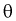
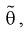
3. Заменяя в п. 2  на оценку  составим уравнение:

4. Откуда определим оценку параметра

 

Метод наибольшего правдоподобия

Этот метод предложен математиком Фишером в 1912 г.
 

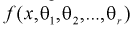
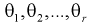
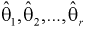
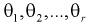
Пусть  – плотность распределения генеральной случайной величины X, где  – неизвестные параметры. Согласно методу, наилучшими оценками  параметров  являются такие, для которых функция правдоподобия L принимает наибольшее значение.

Для непрерывной случайной величины

   (8.11)

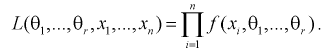
Для дискретной случайной величины

                  (8.12)
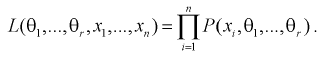
Здесь 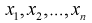– выборка из генеральной случайной величины X.
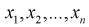
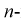
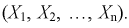
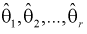
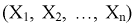
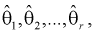
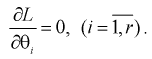
Априорные выборочные значения  – являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности мерного вектора  Согласно методу, для наилучших оценок  случайный вектор  будет иметь наибольшую плотность распределения. То есть надо найти такие оценки  для которых функция правдоподобия L – максимальна. Для этого составляют и решают такую систему уравнений:
                                   (8.13)

Так как функция и ее логарифм достигают экстремума в одной точке, то часто для упрощения решения задачи используют логарифмическую функцию правдоподобия. В случае логарифмической функции правдоподобия составляется система следующих уравнений:
                            (8.14)
 

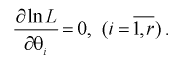
Пример:

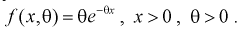
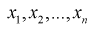
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью  По выборке методом наибольшего правдоподобия найти оценку параметра

 1. Так как нам необходимо оценить один параметр 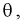 то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):

2. Составим логарифмическую функцию правдоподобия:

3. Для определения максимума логарифмической функции правдоподо­бия составляем и решаем следующее уравнение:

Откуда оценка 0 параметра 0 определяется так:

При сравнение это выражение с оценкой 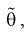 полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.

Свойства оценок

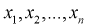
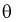
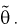
Пусть  – выборка из генеральной совокупности. Обозначим оценку параметра  через  Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от

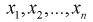
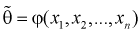
Так как любая выборка типа – случайна, то и выборочные функции  – тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
 

1. Оценка 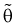 называется несмещенной, если ее математическое ожида­ние совпадает с самим оцениваемым параметром:

В противном случае оценка называется смещенной.

 

Полную погрешность 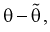 возникшую от замены 0 на 0, можно пред­ставить так:

Таким образом, если оценка несмещенная, то систематическая погреш­ность равна нулю, т. е.

Наиболее опасна систематическая ошибка, если она заранее неизвестна или среднее квадратичное отклонение не очень большое. Среднее значение случайной ошибки

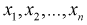
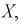
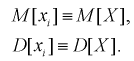
Мы уже отмечали, что – независимые случайные величины, имеющие тот же закон распределения, что и  генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:

                                   (*)

Проверим смещенность оценки математического ожидания выборочной средней 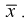 Используя обычные свойства математического ожидания, найдем

 

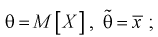
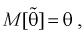
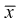
Обозначим  видим, что значит, выборочное среднее  является несмещенной оценкой математического ожидания.

Проверим смещенность оценки дисперсии выборочной дисперсией 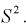 Найдем математическое ожидание от выборочной дисперсии:

То есть дисперсия выборочной средней в 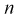 раз меньше дисперсии генеральной случайной величины. Тогда

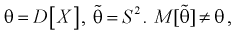
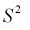
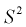
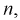
Обозначим  значит, выборочная дисперсия  является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия  является асимптотически несмещенной оценкой, т. к. при  стремящемся к бесконечности, смещение стремится к нулю.

При решении практических задач часто используется несмещенная оцен­ка дисперсии – это модифицированная выборочная дисперсия:

Найдем математическое ожидание от

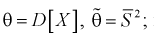
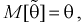
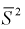
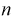
Обозначим  как видим,  значит, оценка  уже несмещенная. При малых  этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии – когда известно математическое ожидание:

Найдем 

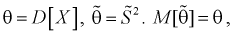
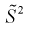
Обозначим  значит, оценка  несмещенная.
 

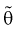
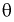
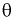
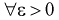
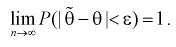
2. Оценка  параметра  называется состоятельной, если она сходит­ся по вероятности к параметру , т. е. если  выполняется:

                            

Условие 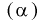на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:

а)

б)

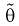
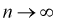
Как видим, оценка  будет состоятельной, если при  смещение устраняется и дисперсия оценки стремится к нулю.
 

Пример:

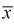
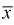
Проверим состоятельность оценки математического ожидания выборочной средней . Ранее мы показали, что  является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем 

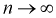
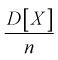
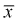
Видим, что при  предел  будет стремиться к нулю, значит условие б) выполняется. Следовательно,  является состоятельной оценкой математического ожидания.

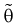
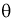
3. Несмещенная оценка  параметра  называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки
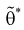
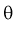
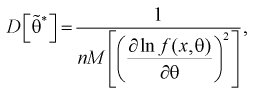
Для определения наименьшей дисперсии эффективной оценки  параметра  применяется формула Рао-Крамера:

                   (8.15)

где 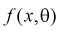 – плотность распределения генеральной случайной величины X.
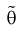
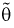
Отметим, если оценка  смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки  взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
 

Пример:

Задана нормальная случайная величина 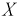 с плотностью распределения

Проверим эффективность оценки математического ожидания выборочной средней .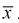

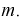
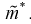
Найдем дисперсию эффективной оценки параметра  Обозначим эффективную оценку Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим

Найдем производную:

Подставим полученное выражение в (8.15): 

Ранее мы показали, что такую же дисперсию имеет 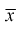 (см. формулу
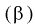
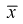
Видим, что правые части формул (8.16) и  совпадают, следовательно, выборочное среднее  является эффективной оценкой параметра

Отметим, что оценки, полученные методом наибольшего правдоподобия, являются состоятельными. Если существуют эффективная оценка, то метод наибольшего правдоподобия позволяет найти ее, но не всегда оценки, полученные этим методом, являются несмещенными.

ЛЕКЦИЯ
16

Статистические
оценки параметров генеральной
совокупности. Статистические гипотезы

1. Определение
   статистической оценки. Точечные
   статистические оценки.

Пусть требуется
изучить количественный признак
генеральной совокупности. Допустим,
что из теоретических соображений удалось
установить, какое именно распределение
имеет признак. Отсюда возникает задача
оценки параметров, которыми определяется
это распределение. Например, если
известно, что изучаемый признак
распределён в генеральной совокупности
по нормальному закону, то необходимо
оценить (приближённо найти) математическое
ожидание и среднеквадратическое
отклонение, так как эти два параметра
полностью определяют нормальное
распределение. Если же имеются основания
считать, что признак имеет распределение
Пуассона, то необходимо оценить параметр
,
которым это распределение определяется.

Обычно в распределении
исследователь имеет лишь данные выборки,
например, значения количественного
признака
,
полученные в результате

наблюдений (здесь и далее наблюдения
предполагаются независимыми). Через
эти данные и выражают оцениваемый
параметр.

Рассматривая

как значения независимых случайных
величин
,
можно сказать, что найти статистическую
оценку неизвестного параметра
теоретического распределения означает
найти функцию от наблюдаемых случайных
величин, которая и даёт приближённое
значение оцениваемого параметра.
Например, как будет показано далее, для
оценки математического ожидания
нормального распределения служит
функция (среднее арифметическое
наблюдаемых значений признака):

.

Итак, статистической
оценкой
неизвестного параметра теоретического
распределения называют функцию от
наблюдаемых случайных величин.
Статистическая оценка неизвестного
параметра генеральной совокупности,
записанная одним числом, называется
точечной.
Рассмотрим следующие точечные оценки:
смещенные и несмещённые, эффективные
и состоятельные.

Для того, чтобы
статистические оценки давали «хорошие»
приближения оцениваемых параметров,
они должны удовлетворять определённым
требованиям. Укажем эти требования.

Пусть

есть статистическая оценка неизвестного
параметра

теоретического распределения. Допустим,
что при выборке объёма

найдена оценка
.
Повторим опыт, то есть извлечём из
генеральной совокупности другую выборку
того же объёма и по её данным найдём
оценку

и т.д. Повторяя опыт многократно, получим
числа
,
которые, вообще говоря, будут различаться
между собой. Таким образом, оценку

можно рассматривать как случайную
величину, а числа
–
как возможные её значения.

Ясно, что если
оценка

даёт приближённое значение

с избытком, то каждое найденное по данным
выборок число

будет больше истинного значения
.
Следовательно, что в этом случае и
математическое (среднее значение)
случайной величины

будет больше, чем
,
то есть
.
Очевидно, что если

даёт приближённое значение

с недостатком, то
.

Поэтому, использование
статистической оценки, математическое
ожидание которой не равно оцениваемому
параметру, приводит к систематическим
(одного знака) ошибкам. По этой причине
естественно потребовать, чтобы
математическое ожидание оценки

было равно оцениваемому параметру. Хотя
соблюдение этого требования, в общем,
не устранит ошибок (одни значения

больше, а другие меньше чем
),
ошибки разных знаков будут встречаться
одинакова часто. Однако соблюдение
требования

гарантирует невозможность получения
систематических ошибок, то есть устраняет
систематические ошибки.

Несмещённой
называют статистическую оценку (ошибку)
,
математическое ожидание которой равно
оцениваемому параметру

при любом объёме выборки, то есть
.

Смещённой
называют статистическую оценку
,
математическое ожидание которой не
равно оцениваемому параметру

при любом объёме выборки, то есть
.

Однако было бы
ошибочным считать, что несмещённая
оценка всегда даёт хорошее приближение
оцениваемого параметра. Действительно,
возможные значения

могут быть сильно рассеяны вокруг своего
среднего значения, то есть дисперсия

может быть значительной. В этом случае,
найденная по данным одной выборки
оценка, например
,
может оказаться весьма удалённой от
среднего значения
,
а значит, и от самого оцениваемого
параметра
.
Таким образом, приняв

в качестве приближённого значения
,
мы допустим большую ошибку. Если же
потребовать, чтобы дисперсия

была малой, то возможность допустить
большую ошибку будет исключена. По этой
причине к статистической оценке
предъявляется требование эффективности.

Эффективной
называют статистическую оценку, которая
(при заданном объёме выборки
)
имеет наименьшую возможную дисперсию.

Далее, при
рассмотрении выборок большого объёма
(
достаточно велико!) к статистическим
оценкам предъявляется требование
состоятельности.

Состоятельной
называют статистическую оценку, которая
при

стремится по вероятности к оцениваемому
параметру, то есть, справедливо равенство:

.

Например, если
дисперсия несмещённой оценки при

стремится к нулю, то такая оценка
оказывается также состоятельной.

Рассмотрим вопрос
о том, какие выборочные характеристики
лучше всего в смысле несмещённости,
эффективности и состоятельности
оценивают генеральную среднюю и
дисперсию.

Пусть изучается
дискретная генеральная совокупность
относительно некоторого количественного
признака
.

Генеральной
средней

называется среднее арифметическое
значений признака генеральной
совокупности. Она вычисляется по формуле:

Замечание:
пусть генеральная совокупность объёма

содержит объекты с различными значениями

признака
.
Представим себе, что из этой совокупности
наудачу извлекается один объект.
Вероятность того, что будет извлечён
объект со значением признака, например
,
очевидно, равна
.
С этой же вероятностью может быть
извлечён и любой другой объект. Таким
образом, величину признака

можно рассматривать как случайную
величину, возможные значения

которой имеют одинаковые вероятности,
равные
.
Нетрудно, в этом случае, найти математическое
ожидание
:

Итак, если
рассматривать обследуемый признак

генеральной совокупности как случайную
величину, то математическое ожидание
признака равно генеральной средней
этого признака:
.
Этот вывод мы получили, считая, что все
объекты генеральной совокупности имеют
различные значения признака. Такой же
итог будет получен, если допустить, что
генеральная совокупность содержит по
несколько объектов с одинаковым значением
признака.

Обобщая полученный
результат на генеральную совокупность
с непрерывным распределением признака
,
определим генеральную среднюю как
математическое ожидание признака:
.

Пусть для изучения
генеральной совокупности относительно
количественного признака

извлечена выборка объёма
.

Выборочной
средней

называют среднее арифметическое значений
признака выборочной совокупности. Она
вычисляется по формуле:

Замечание:
выборочная средняя, найденная по данным
одной выборки есть, очевидно, определённое
число. Если же извлекать другие выборки
того же объёма из той же генеральной
совокупности, то выборочная средняя
будет изменяться от выборки к выборке.
Таким образом, выборочную среднюю можно
рассматривать как случайную величину,
а следовательно, можно говорить о
распределениях (теоретическом и
эмпирическом) выборочной средней и о
числовых характеристиках этого
распределения¹,
в частности, о математическом ожидании
и дисперсии выборочного распределения.

Далее, если
генеральная средняя неизвестна и
требуется оценить её по данным выборки,
то в качестве оценки генеральной средней
принимают выборочную среднюю, которая
является несмещённой и состоятельной
оценкой (предлагаем это
утверждение доказать самостоятельно).
Из сказанного
следует, что если по нескольким выборкам
достаточно большого объёма из одной и
той же генеральной совокупности будут
найдены выборочные средние, то они будут
приближённо равны между собой. В этом
состоит свойство устойчивости
выборочных средних².

Отметим, что если
дисперсии двух совокупностей одинаковы,
то близость выборочных средних к
генеральным не зависит от отношения
объёма выборки к объёму генеральной
совокупности. Она зависит от объёма
выборки: чем объём выборки больше, тем
меньше выборочная средняя отличается
от генеральной. Например, если из одной
совокупности отобран 1% объектов, а из
другой совокупности отобрано 4% объектов,
причём объём первой выборки оказался
большим, чем второй, то первая выборочная
средняя будет меньше отличаться от
соответствующей генеральной средней,
чем вторая.

Для того чтобы
охарактеризовать рассеяние значений
количественного признака

генеральной совокупности вокруг своего
среднего значения, вводят сводную
характеристику – генеральную дисперсию.
Генеральной
дисперсией

называется среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения
,
и вычисляется по формуле:

,
или
.

Для того чтобы
охарактеризовать рассеяние наблюдаемых
значений количественного выборки вокруг
своего среднего значения, вводят сводную
характеристику – выборочную дисперсию.
Выборочной
дисперсией

называется среднее арифметическое
квадратов отклонений наблюдаемых
значений признака выборочной совокупности
от их среднего значения
,
и вычисляется по формуле:

,
или
.

Вычисление
дисперсии, безразлично, выборочной или
генеральной, можно упростить, если
воспользоваться следующей теоремой:
дисперсия
равна среднему квадратов значений
признака минус квадрат общей средней:
.
Действительно, справедливость теоремы
вытекает из преобразований:

Кроме дисперсии
для характеристики рассеяния значений
признака генеральной (выборочной)
совокупности вокруг своего среднего
значения используют сводную характеристику
– среднее квадратическое отклонение.
Генеральным
(выборочным)
средним квадратическим отклонением
называют квадратный корень из генеральной
(выборочной) дисперсии:

().

Далее, пусть из
генеральной совокупности в результате

независимых наблюдений над количественным
признаком

извлечена повторная выборка объёма
:

Значения признака			. . .
частота			. . .
причём

Требуется по данным
выборки оценить (приближённо найти)
неизвестную генеральную дисперсию
.
Если в качестве оценки генеральной
дисперсии принять выборочную дисперсию,
то эта оценка будет приводить к
систематическим ошибкам, давая заниженное
значение генеральной дисперсии.
Объясняется это тем, что как можно
доказать, выборочная дисперсия является
смещённой оценкой генеральной дисперсии
.
Другими словами, математическое ожидание
выборочной дисперсии не равно оцениваемой
генеральной дисперсии, а равно

.

Легко «исправить»
выборочную дисперсию так, чтобы её
математическое ожидание было равно
генеральной дисперсии. Для этого
достаточно умножить

на дробь
.
Сделав это, получим «исправленную
дисперсию», которую обычно принято
обозначать через
:

.

«Исправленная
дисперсия» является, конечно, несмещённой
оценкой генеральной дисперсии.
Действительно

.

Итак, в качестве
оценки генеральной дисперсии принимают
«исправленную дисперсию»

.

Для оценки же
среднего квадратического отклонения
генеральной совокупности используют
соответственно «исправленное» среднее
квадратическое отклонение, которое
равно квадратному корню из «исправленной
дисперсии»:

.

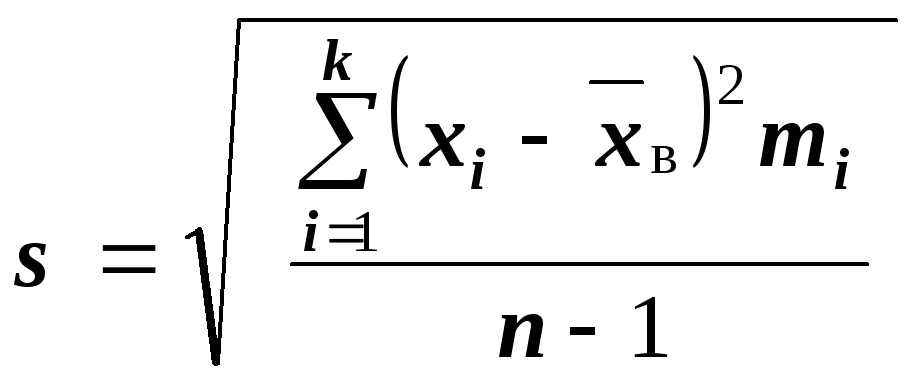
Подчеркнём, что

не является несмещённой оценкой; чтобы
отразить этот факт мы написали и будем
писать далее так: «исправленное» среднее
квадратическое отклонение.

Замечание:
сравнивая формулы

и

видим, что они
отличаются лишь знаменателем. Очевидно,
при достаточно больших значениях

объёма выборки, выборочная и «исправленная»
дисперсии различаются мало. На практике
пользуются «исправленной дисперсией»,
если примерно
.

1
Данное распределение называют выборочным.

2
Полученные выводы применимы и для
бесповторной выборки, если её объём
значительно меньше объёма генеральной
совокупности. Это положение часто
используется на практике.

7

Соседние файлы в папке Теор.вер. (лекции)

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Статистическая оценка — это статистика, которая используется для оценивания неизвестных параметров распределений случайной величины.

Определение[править | править код]

Например, если  — это независимые случайные величины, с заданным нормальным распределением , то будет средним арифметическим результатов наблюдений.

Задача статистической оценки формулируется так:

Пусть  — выборка из генеральной совокупности с распределением . Распределение имеет известную функциональную форму, но зависит от неизвестного параметра . Этот параметр может быть любой точкой заданного параметрического множества . Используя статистическую информацию, содержащуюся в выборке , сделать выводы о настоящем значении параметра .

Точечная оценка[править | править код]

Оценка является случайной величиной так как представляет собой функцию от случайных величин ^[1]:

Функция распределения оценки зависит от распределения величины (и от параметра ), а также от размера выборки .

Оценка может обладать рядом «хороших» свойств^[1]:

На практике не всегда есть возможность получать оценки с заданными свойствами, из-за чего приходится довольствоваться компромиссными вариантами^[1].

Интервальная оценка[править | править код]

Для оценивания промежутка, на котором лежит оцениваемый параметр , можно использовать следующие методы^[2]:

• Метод доверительных интервалов
• Метод фидуциальных интервалов
• Достоверный Байесовский интервал (англ. Credible interval)

См. также[править | править код]

• Достаточная статистика

Примечания[править | править код]

Литература[править | править код]

•  Вентцель Е. С. Теория вероятностей. — М.: Наука, 1969.
• Кендалл Морис Дж., Стьюарт Алан. Статистические выводы и связи. — М.: Наука. 1973.

Ссылки[править | править код]

• vseslova — Статистические оценки
• Shao, Jun (1998), Mathematical Statistics, New York: Springer, ISBN 0-387-98674-X
• Bol’shev, L. N. (2001), Statistical Estimator, in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104

Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.

Найти статистическую оценку неизвестного параметра распределения — найти функцию от наблюдаемых случайных величин, которая даст приближенное значение оцениваемого параметра.

Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.

«Статистические оценки параметров распределения» 👇

Генеральная и выборочная средние

Величины генерального и выборочного среднего можно найти по следующим формулам:

1. Если значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$, то

1. Если значения вариант $x_1, x_2,dots ,x_k$ различны, то

С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:

Среднее отклонение обладает следующими свойствами:

1. $sum{n_ileft(x_i-overline{x}right)=0}$

2. Среднее значение отклонения равно нулю.

Генеральная, выборочная и исправленная дисперсии

Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:

Генеральная дисперсия:

Выборочная дисперсия:

С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:

В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:

Также вводится понятие исправленного стандартного отклонения:

Пример решения задачи