Расчет ставки дисконтирования
Онлайн калькулятор
Ставка дисконтирования используется для приведения будущей стоимости к стоимости на текущий момент. Эта операция называется дисконтированием и отражает тот экономический факт, что сумма денег имеющаяся в данный момент, имеет большую реальную стоимость, чем равная ей сумма, которая появится в будущем. Расчет ставки дисконтирования производится по-разному в зависимости от задачи.
Расчет окупаемости инвестиций
Расчет ставки дисконтирования необходим для оценки экономической эффективности инвестиций, определения срока окупаемости и для дисконтирования денежных потоков, иными словами, для перерасчета стоимости потоков будущих доходов и расходов в стоимость на настоящий момент.
В этом случае в качестве ставки дисконтирования принимается один из вариантов:
- Доходность альтернативного проекта.
- Стоимость доступного кредита.
- WACC — cредневзвешенная стоимость капитала.
- Экспертная оценка.
- Желаемая доходность инвестиционного проекта.
- Кумулятивный метод, базирующийся на оценке рисков инвестиционного проекта обусловленных разными факторами. Расчет ставки дисконтировния выполняется путем сложения рисков, выраженных в процентах.
Особую роль при расчете инвестиционнго проекта имеет IRR (внутренняя норма доходности) — значение ставки дисконтирования при которой NPV проекта равно 0.
Задача обратная наращению (начислению процентов)
В финансовых расчетах часто приходится решать задачу обратную наращению (задачу дисконтирования): по известной наращенной сумме найти начальную сумму. Например, какую сумму положить на депозит, чтобы через 5 лет получить 500 тыс. руб.
Введем обозначения:
PV — present value, современная величина или первоначальная сумма.
FV — future value, будущая величина или наращенная сумма.
I = (FV – PV) — interest money, процентные деньги, проценты. Представляют собой сумму дохода.
Оценка доходности финансовых операций по величине процентных денег I редко используется, т.к. зависит от первоначальной суммы PV и срока наращения. Более удобным показателем является процентная ставка, характеризующая скорость наращения
r = I/PV = (FV-PV)/PV
r = I/PV = (FV-PV)/PV * 100 (%)
r— interest, процентная ставка.
Онлайн калькулятор
Расчет процентной ставки
r =
Обычно процентная ставка известна из условий финансовой операции (например, из условий депозитного или кредитного договора), тогда для наращенной суммы можно записать:
FV = PV*(1+r)
Таким образом, зная процентную ставку и начальную сумму, мы определяем наращенную сумму. Эта формула верна для случая одного периода начисления процентов, для случая нескольких периодов начисления с зачислением процентов на депозит и даленейшим начислением процента на процент, надо использовать формулу сложных процентов.
Онлайн калькулятор
Расчет наращенной суммы
FV =
См. также:
- Формулы расчета процентов
- Формулы расчета сложных процентов и выбор вклада
При решении задач дисконтирования надо решить обратную задачу: зная наращенную сумму, определить начальную сумму, или сумму в другой предшествующий момент. Для этого по аналогии с процентной ставкой определим ставку дисконтирования (учетную ставку):
d = I/FV = (FV-PV)/FV
d — discount rate, ставка дисконтирования, учетная ставка.
Онлайн калькулятор
Расчет ставки дисконтирования
d =
Зная ставку дисконтирования и наращенную сумму, решаем задачу дисконтирования (определяем начальную сумму):
PV = FV*(1-d)
Онлайн калькулятор
Расчет начальной суммы (дисконтирование)
PV =
Ставка дисконтирования и процентная ставка связаны соотношениями:
r = d * (FV/PV)
d = r * (PV/FV)
Кроме того, т.к. процентная ставка определяется по отношению к начальной сумме, а ставка дисконтирования — к наращенной, процентная ставка больше ставки дисконтирования.
Инвестиционный калькулятор
Инвестиционный калькулятор для оценки NPV (чистой приведенной стоимости) проекта
Калькулятор
Ставка дисконтирования
%
Период
{{ calcNVP.dataSetCount() }}
год
| Период (год) | Инвестиции (IC) | Приток ДС (CI) | Отток ДС (CO) | Денежный поток, CF | Дисконтированный денежный поток, DCF |
|---|---|---|---|---|---|
| 0 | |||||
| {{ $index + 1 }} | |||||
| NPV |
NPV > 0, проект можно принять
NPV < 0, проект лучше отвергнуть
Метод расчета
Чистая приведенная стоимость инвестиционного проекта представляет немедленное изменение в стоимости компании, как только проект принят.
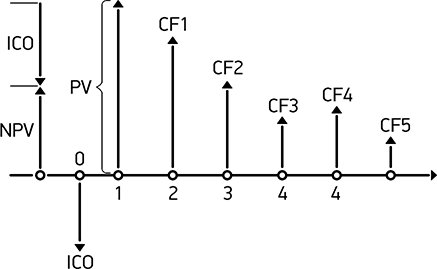
ICO – Первоначальные инвестиции
CH n – Денежный поток n-го года
NPV – Чистая приведенная стоимость
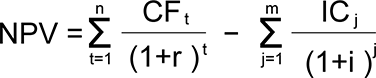
Правило метода: если NPV >= 0 – проект принимается, если NPV < 0 – проект отклоняется.
Когда NPV проекта позитивная – проект создает стоимость, когда негативная – разрушает.
Инвестиционный калькулятор для оценки DPP (дисконтированного срока окупаемости)
Калькулятор
Ставка дисконтирования
%
Период
{{ calcDPP.dataSetCount() }}
год
| Период (год) | Инвестиции (IC) | Приток ДС (CI) | Отток ДС (CO) | Денежный поток, CF | Дисконтированный денежный поток, DCF |
|---|---|---|---|---|---|
| 0 | |||||
| {{ $index + 1 }} | |||||
DPP (годы): {{ calcDPP.calcDPPValue() | number:2 }}.
Срок окупаемости дольше ожидаемого, проект лучше отвергнуть
Метод расчета
Срок окупаемости проекта – это срок, за который денежный поток должен превысить объем вложенных в проект инвестиций.
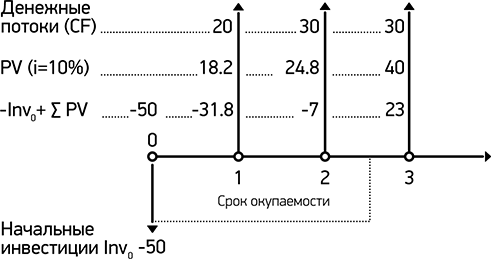
DPP – Срок, за который выполняется условие:
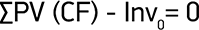
Инвестиционный калькулятор для оценки PI (индекс рентабельности) проекта
Калькулятор
Ставка дисконтирования
%
Период
{{ calcPI.dataSetCount() }}
год
| Период (год) | Инвестиции (IC) | Приток ДС (CI) | Отток ДС (CO) | Денежный поток, CF | Дисконтированный денежный поток, DCF |
|---|---|---|---|---|---|
| 0 | |||||
| {{ $index + 1 }} | |||||
PI = {{ calcPI.calcPI() | number:2 }}, вложение капитала является эффективным, проект можно принять
PI = {{ calcPI.calcPI() | number:2 }}, вложение капитала является не эффективным, проект лучше отвергнуть
Метод расчета
Индекс рентабельности проекта – показывает, сколько единиц
современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат.
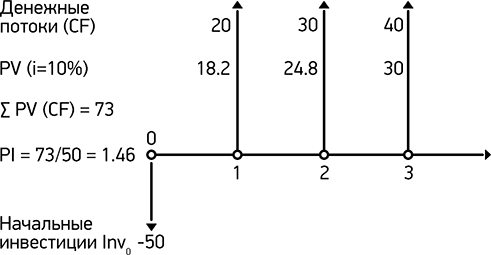

Дисконтированная (приведённая, текущая) стоимость: определение
Дисконтированная (приведённая, текущая) стоимость (от англ. “present value” или PV),— оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временной ценности денег).
Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть другие факторы, снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.
Дисконтированная стоимость некоторой будущей суммы X равна денежной сумме, при инвестировании которой сейчас (с доходностью, равной ставке дисконтирования), в будущем (в тот же момент времени) будет получена сумма X. Дисконтированная стоимость потока платежей равна сумме дисконтированных стоимостей отдельных платежей, входящих в этот поток. Она фактически равна дисконтированной величине будущей стоимости денежного потока (сумма, которая будет получена в будущем, если денежный поток инвестировать в моменты получения платежей под ставку дисконтирования).
Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:
- доходности альтернативных вложений;
- стоимости привлечения (заимствования) средств;
- инфляции;
- срока, через который ожидается будущий поток платежей;
- риска, связанного с данным будущим потоком платежей;
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Практическое объяснение: ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб., которые будут получены через пять лет.
Формула для расчета дисконтированного денежного потока:
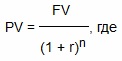
PV — текущая стоимость;
r — ставка дисконтирования;
n — количество лет.
Чем дольше срок получения инвестиции и чем выше ставка дисконтирования, тем меньше текущая стоимость.
Например, планируемые к получению 1000 рублей через 1 год инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 869,57 рублям; для планируемых к получению 1000 рублей через 2 года инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 756,14 рублям; для планируемых к получению 1000 рублей через 3 года инвестирования при ставке дисконтирования 15% эквивалентны сегодняшним 657,52 рублям.
В данном примере величина 869,57 рублей является текущей стоимостью величины 1000 рублей, полученных от инвестиции сроком на 1 год при ставке дисконтирования 15%.
На тему этой методики существуют примеры задач на приведенную стоимость с решениями.
Задачи на расчет приведенной стоимости
Задача №1. Какой необходимо сделать вклад, чтобы через 10 лет получить 12500 рублей, при процентной ставке равной 11,7%?
Рассчитаем дисконтированную стоимость:
PV = 12500 / (1 + 0,117)10 = 4134 рубля.
Ответ. При данных условиях сумма вклада равна 4134 рубля.
Задача №2. Через сколько лет на счете в банке будет сумма в 5600 рублей, если вложили 3400 рублей при коэффициенте дисконтирования 15,65% годовых?
Преобразуем формулу приведенной стоимости таким образом, чтобы выделить срок вложения денег:
(1 + r)n = PV / FV;
1,1565n = 5600 / 3400 = 1,6471;
n = log 1,1565 1,6471 = 3,43 года.
Ответ. Через 3,43 года на счете в банке будет вышеуказанная сумма.
При расчете числа лет необходимо учитывать, что в формуле подразумевается целое число лет и цифры, рассчитываемые после запятой, имеют приблизительные значения, характеризующие близость к целому значению лет.
Задача №3. Рассчитайте, при какой учетной ставке ожидаемая к поступлению сумма в 5000$ соответствует текущему значению 2000$, если время дисконтирования 6 лет.
Преобразуем формулу приведенной стоимости таким образом, чтобы выделить учетную ставку:
r = (PV / FV)1/n — 1;
r = (5000 / 2000)1/6 — 1;
r = 0,16499 или 16,499%.
Ответ. При учетной ставке 16,499% будущая стоимость будет соответствовать исходной сумме.
Задача №4. Какую сумму нужно положить на счет в банк, чтобы через 4 года иметь 2000$, при ставке равной 9% годовых.
Рассчитаем приведенную стоимость 2000$ при ставке равной 9% и сроком 4 года:
PV = 2000 / (1 + 0,09)4 = 1416 $.
Ответ. Исходная сумма, необходимая для вклада, равна 1426$.
#Калькуляторы
Calculate the discounted present value (DPV) of an investment using the discounted cash flow (DCF) model.
Discounted Present Value (DPV):
| Growth Value: | |
| Terminal Value: | |
| Total Value: |
Learn how we calculated this below
scroll down
On this page:
-
Calculator
-
How to Calculate a Discounted Cash Flow Analysis
-
Discount Rate and WACC
-
Discounted Cash Flow Formula
-
Discounted Cash Flow Analysis Example
-
Discounted Cash Flow Limitations
-
Discounted Cash Flow vs. Net Present Value
-
References
How to Calculate a Discounted Cash Flow Analysis
Discounted cash flow (DCF) analysis is a method that can be used to value a particular investment based on its expected future cash flows. This can be used for valuing a stock or a particular project a company is considering.
In the case of a stock, future cash flows would be dividends. If a company is considering whether or not to invest in a project, the cash flows can be cash coming into the business, such as with a machine that improves the product and increases revenue.
Cash flows can also be in the form of savings, such as with video conferencing technology that may reduce the expenses related to office space.
A DCF analysis takes all future cash flows and discounts them using the discount rate or weighted average cost of capital (WACC). An investor/company can choose whether a discount rate or WACC is most appropriate for their analysis.
Discount Rate and WACC
The discount rate and weighted average cost of capital are the rates that investors and businesses use to discount future cash flows.
The discount rate is the rate that is used for investments of similar risk. If an investor typically earns 8% on his investments, that is the discount rate he will use in evaluating potential new investments.
The level of risk is different for different types of investments, so using a discount rate that does not align with the particular investment could provide misleading results.
The WACC is the weighted average of the cost of debt and the cost of equity. This is the return that business owners would require their business to make with an investment. If the investment doesn’t return at least as much as its WACC, the investment should be rejected.
Discounted Cash Flow Formula
The discounted cash flow formula below shows how the discount rate and WACC are applied.
The discounted cash flow formula is shown below:[1]
DCF = frac{CF_{1}}{(1 + r)^{1}} + frac{CF_{2}}{(1 + r)^{2}} + cdots + frac{CF_{n}}{(1 + r)^{n}}
[formula may scroll beyond screen]
where:
DCF = discounted cash flow
CF = cash flow for a given period
r = discount rate
As the formula shows, each future cash flow is discounted by 1 plus the discount rate or WACC raised to the power of the time period. After each future cash flow is discounted, all the cash flows are summed up to arrive at the discounted cash flow.

Discounted Cash Flow Analysis Example
For example, to help explain how the discounted cash flow calculation works, let’s say an investor is deciding whether or not to buy a stock. The company will pay a $1.00 dividend next year. Based on historical data, he anticipates the dividend will then grow by 2% for 20 years and then by 1% for 20 years after that.
The investor will then plan on selling the stock. They typically make 8% on their investments, so this will be the discount rate.
Since this involves a period of 40 years, it is much simpler to plug these numbers into the calculator than work the formula by hand. You will need the cash flow and discount rate plus the following variables for the calculation:
- Growth Rate: The rate at which the cash flow is initially projected to grow each year.
- Growth Period: The number of years for this initial growth period.
- Terminal Rate: The rate at which the cash flow is projected to grow each year after the initial growth period.
- Terminal Period: The number of years the cash flow will grow at the terminal rate.
In this example, the cash flow will be $1. The discount rate is 8%. The growth rate is 2% and the growth period is 20 years. The terminal rate is 1% and the terminal period is 20 years.
After plugging these numbers into the discounted cash flow calculator above, we get a total DCF of $14.98. If the stock is trading for anything less than $14.98, the investor would want to purchase it because the present value of all future cash flows is greater than the price of the stock.
But, if it is trading for more than $14.98, the investor should not buy the stock.
Now let’s look at an example of a company deciding whether or not it wants to move forward with a project. It anticipates making a $100,000 investment in a technology that will increase its revenues immediately by $25,000.
For the next 2 years after that, the increase in revenue will be 5% higher than the prior year. Then for the next 3 years, revenue will only be 2% higher than the previous year. The company has a WACC of 10%. Is this a smart investment?
Since this is only for 4 years, we can use either the discounted cash flow formula or the calculator above. Let’s use the formula first, and then you can confirm in the calculator. The table below gives the results.
| Period | Cash Flow | Discounted Cash Flow |
|---|---|---|
| 1 | 26,250.00 | 23,863.64 |
| 2 | 27,562.50 | 22,778.93 |
| 3 | 28,113.75 | 21,122.28 |
| 4 | 28,676.03 | 19,586.11 |
| 5 | 29,249.55 | 18,161.67 |
| Total | 139,851.82 | 105,512.62 |
Here again, we see that the investment is worth it. The DCF of $105.512.62 is greater than the initial investment of $100,000. If the DCF had been less than the initial investment, the company would not have gone through with the technology investment.
To find the breakeven point, use our IRR calculator. It shows what the discount rate would need to be to make the cash flows equal to the initial investment.
Discounted Cash Flow Limitations
While the DCF analysis is a helpful tool for planning purposes, there are a handful of limitations.
First, estimating forecasts, such as future cash flows and growth rates, far in advance is very difficult. So while it does provide an investor or business a framework to make a decision, whether or not the correct decision was made won’t be known until the end of the time period.
Also, not all companies pay a dividend. Newer companies typically won’t pay a dividend and instead will reinvest income back into the business. In this case, the DCF model computes a value of $0 for these companies. We know that newer companies aren’t worth $0, so a DCF analysis can’t be used for them.
Negative amounts can’t be used in the DCF analysis either. If a business expects to have to repair a machine after a certain number of years, this can’t be factored into the analysis. This limitation can also apply to an investment in which a business may reduce its dividend in a recession.
Discounted Cash Flow vs. Net Present Value
The discounted cash flow is the sum of all the discounted cash flows. The net present value (NPV) is what is left over after the initial investment is made. So the NPV = DCF – initial investment.
DCF by itself doesn’t give any direction on the decision to be made. The NPV does. If the NPV of a project or investment is greater than $0, the investment should generate a return.[2]
Under these assumptions, a return of at least the discount rate or WACC will be achieved. There are other calculators to calculate the rate of return, such as our ROI calculator and rate of return calculator.
If the NPV is less than $0, the investment should not be made. In an earlier example, we had a business trying to decide if it should invest $100,000 in new technology. The DCF was $105,512.62. Therefore, the NPV was positive $5,512.62 and the business should have made the investment.
Our NPV calculator is similar to the discounted cash flow calculator, but each of the cash flows needs to be entered. If there is only one future cash flow, then you can use a present value calculator, which will calculate what the value of that future cash flow is today, discounted at a certain rate for a period of time.
The larger the NPV, the better. This provides an additional margin for error in the forecasts.
Diskonteeritud neto sissetuleku kalkulaator
Калькулятор чистого дисконтированного дохода (NPV)
|
||||
|
|
||||
| Ставка дисконтирования | % | |||
| Срок | год(а) / лет | |||
|
|
||||
| Год | Доходы проекта | Первоначальные инвестиции/ Расходы проекта |
Чистый поток платежей | Дисконтированные платежи |
|---|---|---|---|---|
| 0 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| Сумма доходов | Сумма расходов | Сумма потоков | ||
| Итого: | ||||
|
|
||||
Результат |
||||
|
|
||||
| Чистый дисконтированный доход (ЧДД / NPV) | ||||
| Индекс прибыльности (англ. Profitability Index) | ||||
by vorob77
Если Вам нужен любой из этих калькуляторов на Ваш сайт, или для локального использования? напишите мне, я вышлю скрипт нужного калькулятора за символичную плату в размере 6 евро или 250р.
Связаться со мной.
JComments
ВКонтакте
Facebook
У Вас недостаточно прав для комментирования, зарегистрируйтесь пожалуйста.
Download SocComments v1.3
