Как найти степень десятичного числа

Как найти степень десятичного числа

Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя – как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с такого проверочного действия, как формулирование базовых определений.

Определение 1

Возвести число в степень – это вычисление значения степени некоторого числа.

То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0,5 в пятую степень”, это следует понимать как “вычислите значение степени (0,5)5.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:

Как возвести число в натуральную степень

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Пример 1

Условие: возведите -2 в степень 4.

Решение

Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.

Возьмем пример посложнее.

Пример 2

Вычислите значение 3272

Как будем решать

Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 327·327=237·237=52949=103949

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Пример 3

Выполните возведение в квадрат числа π.

Решение

Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.

Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

a1=a

Это понятно из записи Как возвести число в натуральную степень.

От основания степени это не зависит.

Пример 4

Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно  73.

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.

Пример 5

Примеры:

50=1, (-2,56)0=1230=1

00- не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.

Пример 6

Выполните возведение 2 в степень -3.

Решение 

Используя определение выше, запишем: 2-3=123

Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.

Тогда ответ таков: 2-3=123=18

Пример 7

Возведите 1,43 в степень -2.

Решение 

Переформулируем: 1,43-2=1(1,43)2

Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: 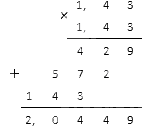Как возвести число в целую степень

В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1,43)-2=1000020449

Отдельный случай – возведение числа в минус первую (минусовую) степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.

Пример 8

Пример: 3−1=1/3

913-1=13964-1=164 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.

Определение 2

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.

У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.

Проиллюстрируем на примере.  

Пример 9

Вычислите 8-23.

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23

Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14

Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2

После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.

Пример 10

Возведите 44,89 в степень 2,5.

Решение 

Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.

А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107

Ответ: 13 501,25107.

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную – значения не имеет: 0-43.

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Пример 11

Вычислите приближенное значение 2 в степени 1,174367…. 

Решение

Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.

Возведение степени в степень 

Как степень возвести в степень? Рассмотрим пример.

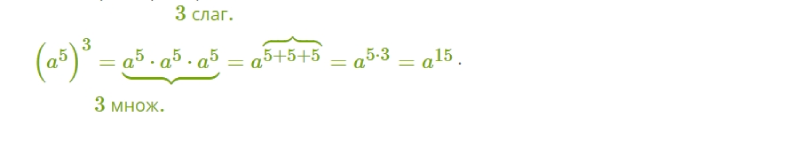Возведение степени в степень Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ. 

Здесь а – это любое число, а n и m – натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.

Все примеры воззведения в степень можно найти в интернете в удобных таблицах.

Источник

При возведении в степень десятичной дроби нужно внимательно следить за положением запятой в ответе. Количество цифр после запятой будет равно количеству цифр в исходной дроби, умноженному на степень, в которую мы возводим эту дробь.

Например, 0,3 в квадрате это 0,09.

0,32 = 0,3 · 0,3 = 0,09

А 0,3 в кубе будет иметь 3 знака после запятой, то есть

0,3⋅0,3⋅0,3=0,027

То есть достаточно возвести в степень число, записанное без запятой, а потом отсчитать справа необходимое количество цифр и поставить запятую.

Например, 2,5 в квадрате. Возведём в квадрат 25, используя таблицу квадратов. 25 в квадрате = 625. У нас был один знак после запятой, мы возводили во вторую степень, значит, в результате будет два знака после запятой, то есть 2,5 в квадрате = 6,25.

Разбор заданий тренировочного модуля

1. Вычислить.

Чтобы возвести в третью степень число 0,6, умножим его само на себя три раза и в ответе отделим запятой справа три знака. Получили 0,216.

2. Вычислить.

Возведём 1,5 в квадрат. Используем таблицу квадратов.15 в квадрате = 225, значит 1,5 в квадрате 2,25.

Вычтем: 2,25 – 0,25 = 2.

3. Вычислить.

Здесь в степень нужно возвести результат действия в скобках.

0,9 – 0,4=0,5

Возведём 0,5 в третью степень. 5 в третьей степениравно 125. Отсчитаем справа три цифры и поставим запятую. Получим 0,125.

Отметьтесь на уроке

Источник

Как возвести число в десятичную степень

Ну что други мои!? Окунемся в десятичные дроби числа!? Число будет положительным, степень тоже будет положительной – почему!? Да просто потому, что если еще и приплетать отрицательную степень, то крышу сорвет однозначно!

Видео: Как возвести число в десятичную степень

Как возвести число в десятичную дробь!?

У нас есть число в десятичной дроби… нам нужно узнать, чему оно равно!?

9765625 0.2

Вообще самый простой способ воспользоваться калькулятор, который уже давно мы разрабатываем!
Но если вам нужно разобраться, то без примера никак не обойтись…
Начнём с картинки:

Как возвести число в десятичную степень

Что вы вынесли из картинки!? Первое, что вы должны были сообразить, что десятичную степень числа нужно преобразовать в дробную… тогда и будет понятно, что делать с этой десятичной дробью!

0.2 = 2/10 = 1/5

Отсюда мы понимаем, что нам требуется всего то… извлечь корень 5 степени из нашего числа.
И здесь уже никак без калькулятора .. никаким другим способом извлечь пятую степень из числа…я не знаю…

9765625 1/5 = 25

Как извлечь десятичную дробь на калькуляторе!?

У нас есть свой собственный Калькуттой, на котором можно извлечь десятичную степень числа!
Для примера давайте возьмем число 9765625 в дробной степени 0.2.
Я специально взял число побольше, пример не из интернета. Чтобы это выглядело довольно внушительно! Как это число можно вообще возвести в десятичную дробь!
Когда у вас есть калькулятор, который это умеет, то все становится очень легко и просто!
1.Вводим число.
Как возвести число в десятичную степень
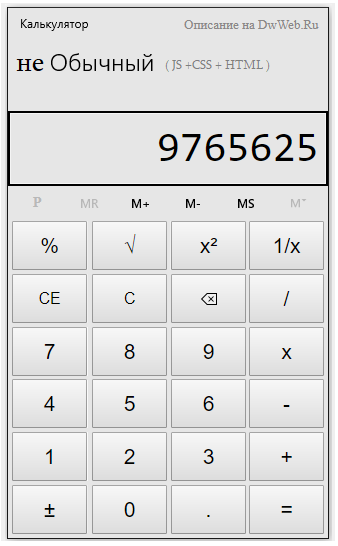
2.Нажимаем кнопку степени
Как возвести число в десятичную степень
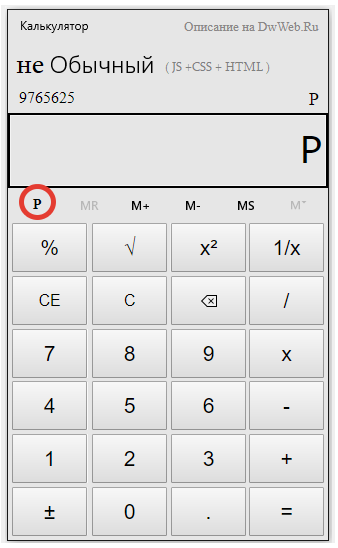
3.Вводим десятичную дробь.
Как возвести число в десятичную степень

4.Нажимаем равно.
Как возвести число в десятичную степень
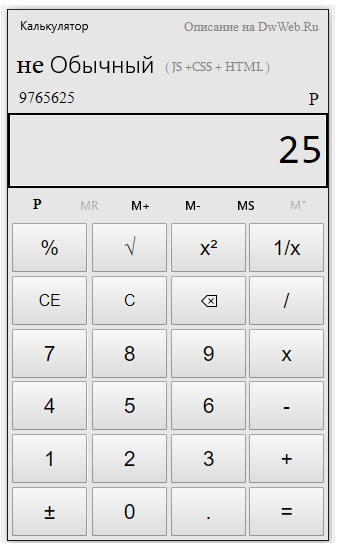
Ну вот собственно мы и посчитали десятичную степень числа.

Написать что-нибудь…

число в десятичной степени ,
степень числа десятичной дроби ,
как возвести число в десятичную степень ,
десятичная запись степени числа ,
возведение числа в десятичную степень ,
как перевести число в десятичную степень ,
десятичные степени чисел решение ,
число в десятичной степени как решать ,
как возвести число в десятичную дробную степень ,
возведение числа в степень десятичной дроби ,
как считать числа с десятичными степенями ,
умножение десятичных дробей на число в степени ,
как посчитать число в десятичной степени,
число 110111 во 2 степени в десятичную ,
как посчитать число в степени десятичной дроби ,
как найти число в десятичной степени ,
возведение числа в отрицательную десятичную степень ,
как возвести число в десятичную степень формула,

Источник

Лучший ответ

Талаев Михаил

Профи

(794)


11 лет назад

переведи в неправильную дробь это десятичное число, например 2 в степени 2,3
2,3 это 23/10 значит все равно корень десятой степени из двух в 23 степени

Остальные ответы

sdfg sdfg

Ученик

(240)


11 лет назад

нужно просто разделить это число на 10 и получившееся число делить на 10 и до тех пор, пока это станет невозможно сделать

Дмитрий Мордовин

Знаток

(310)


11 лет назад

Можно представить в виде произведения: 5^2*5^0.3=25*5^0.3=25*5^(3/10)=25*(корень 10-й степени) из 125

Степан

Оракул

(94371)


11 лет назад

Вычислить с использованием таблиц 2,3 Lg5. От полученного числа найти антилогарифм.

Владислав Сидоров

Ученик

(124)


5 лет назад

я не знаю

Источник


Download Article


Download Article

Calculating exponents is a basic skill students learn in pre-algebra. Usually you see exponents as whole numbers, and sometimes you see them as fractions. Rarely do you see them as decimals. When you do see an exponent that is a decimal, you need to convert the decimal to a fraction. Then, there are a number of rules and laws regarding exponents you can use to calculate the expression.

  1. Image titled Solve Decimal Exponents Step 1

    1

    Convert the decimal to a fraction. To convert a decimal to a fraction, consider place value. The denominator of the fraction will be the place value. The digits of the decimal will equal the numerator.[1]

  2. Image titled Solve Decimal Exponents Step 2

    2

    Simplify the fraction, if possible. Since you will be taking a root corresponding to the denominator of the exponent’s fraction, you want the denominator to be as small as possible. Do this by simplifying the fraction. If your fraction is a mixed number (that is, if your exponent was a decimal greater than 1), rewrite it as an improper fraction.

    Advertisement

  3. Image titled Solve Decimal Exponents Step 3

    3

    Rewrite the exponent as a multiplication expression. To do this, turn the numerator into a whole number, and multiply it by the unit fraction. The unit fraction is the fraction with the same denominator, but with 1 as the numerator.

  4. Image titled Solve Decimal Exponents Step 4

    4

  5. Image titled Solve Decimal Exponents Step 5

    5

    Rewrite the base as a radical expression. Taking a number by a rational exponent is equal to taking the appropriate root of the number. So, rewrite the base and its first exponent as a radical expression.

  6. Image titled Solve Decimal Exponents Step 6

    6

    Calculate the radical expression. Remember that the index (the small number outside the radical sign) tells you which root you are looking for. If the numbers are cumbersome, the best way to do this is using the {sqrt[ {x}]{y}} feature on a scientific calculator.

  7. Image titled Solve Decimal Exponents Step 7

    7

    Calculate the remaining exponent. You should now have a whole number as an exponent, so calculating should be straightforward. You can always use a calculator if the numbers are too large.

    8. Advertisement

  1. Image titled Solve Decimal Exponents Step 8

    1

    Calculate the following exponential expression: 256^{{2.25}}.

  2. Image titled Solve Decimal Exponents Step 9

    2

    Convert the decimal to a fraction. Since 2.25 is greater than 1, the fraction will be a mixed number.

  3. Image titled Solve Decimal Exponents Step 10

    3

    Simplify the fraction, if possible. You should also convert any mixed numbers to improper fractions.

  4. Image titled Solve Decimal Exponents Step 11

    4

    Rewrite the exponent as a multiplication expression. Since {frac {9}{4}}={frac {1}{4}}times 9, you can rewrite the expression as 256^{{{frac {1}{4}}times 9}}.

  5. Image titled Solve Decimal Exponents Step 12

    5

    Rewrite the exponent as a power of a power. So, 256^{{{frac {1}{4}}times 9}}=(256^{{{frac {1}{4}}}})^{{9}}.

  6. Image titled Solve Decimal Exponents Step 13

    6

    Rewrite the base as a radical expression. 256^{{{frac {1}{4}}}}={sqrt[ {4}]{256}}, so you can rewrite the expression as ({sqrt[ {4}]{256}})^{{9}}.

  7. Image titled Solve Decimal Exponents Step 14

    7

    Calculate the radical expression. {sqrt[ {4}]{256}}=4. So, the expression is now (4)^{{9}}.

  8. Image titled Solve Decimal Exponents Step 15

    8

    Calculate the remaining exponent. (4)^{{9}}=4times 4times 4times 4times 4times 4times 4times 4times 4=262,144. So, 256^{{2.25}}=262,144

    9. Advertisement

  1. Image titled Solve Decimal Exponents Step 16

    1

    Recognize an exponential expression. An exponential expression has a base and an exponent. The base is the large number in the expression. The exponent is the smaller number.[4]

  2. Image titled Solve Decimal Exponents Step 17

    2

    Identify the parts of an exponential expression. The base is the number that is being multiplied. The exponent tells you how many times the base is being used as a factor in the expression.[5]

    • For example, 3^{{4}}=3times 3times 3times 3=81.

  3. Image titled Solve Decimal Exponents Step 18

    3

    Identify a rational exponent. A rational exponent is also called a fractional exponent. It is an exponent that takes the form of a fraction.[6]

    • For example, 4^{{{frac {1}{2}}}}.

  4. Image titled Solve Decimal Exponents Step 19

    4

    Understand the relationship between radicals and rational exponents. Taking a number to the {frac {1}{2}} power is like taking the square root of the number. So, x^{{{frac {1}{2}}}}={sqrt {x}}. The same is true for other roots and exponents. The denominator of the exponent will tell you which root to take:[7]

  5. Image titled Solve Decimal Exponents Step 20

    5

    Understand the exponential law of powers of powers. This law says that (x^{{a}})^{{b}}=x^{{ab}}. In other words taking an exponent to another power is the same as multiplying the two exponents.[8]

    6. Advertisement

Add New Question

  • Question

    How can you easily calculate a decimal exponent?

    David Jia

    David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

    David Jia

    Academic Tutor

    Expert Answer

    Support wikiHow by
    unlocking this expert answer.

    First, take the decimal and convert it to a fraction. The numerator of the fraction is an exponent and the denominator is going to be a root. For example, if you have a number like 8^2/3, you would take the cube root of 8 first, which is 2, then square that to get 4.

  • Question

    Why do you calculate the root before the exponent?

    David Jia

    David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

    David Jia

    Academic Tutor

    Expert Answer

  • Question

    How do I find 15^1.4?

    Donagan

    First convert 1.4 to 14/10, and reduce to 7/5. An exponent of 7/5 means first raising to the seventh power and then finding the fifth root (or first finding the fifth root and then raising to the seventh power). Thus, in this case you would raise 15 to the seventh power and then find that number’s fifth root.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Video

References

  1. ↑ David Jia. Academic Tutor. Expert Interview. 14 January 2021.

About This Article

Article SummaryX

To solve a decimal exponent, start by converting the decimal to a fraction, then simplify the fraction. Next, rewrite the fraction as a multiplication expression. To finish, rewrite the exponent as the power of a power, then turn the base and its first exponent into a radical expression by finding the root of the number. Calculate the radical expression, using the x root y function on a calculator if necessary, and the remaining exponent from the exponent. For tips on understanding exponents, including how to identify a rational exponent, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 296,961 times.

Reader Success Stories

  • Miri Mampoumi

    Miri Mampoumi

    Feb 20, 2019

    “I’ve never understood math exceptionally, but as always, the internet is the key base of knowledge. This has…” more

Did this article help you?

Источник

Добавить комментарий