
Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
В соответствии со сказанным химический потенциал ϕ является обобщенной силой, а изменение числа молей данного вещества — обобщенной координатой.
На основании рассуждений, аналогичных изложенным выше, и с учетом уравнения (5.61), которое применительно к принятому в этом параграфе спо-
|
собу выражения количества вещества через число молей имеет вид: |
|||||||||||||||||||||
|
ϕi = |
∂Φ |
= |
∂F |
= |
∂H |
= |
∂U |
, |
|||||||||||||
|
——— |
p,T,M |
——— |
V,T,M |
——— |
p,S,M |
——— |
V,S,M |
||||||||||||||
|
∂M |
i |
j |
∂M |
i |
j |
∂M |
i |
j |
∂M |
i |
j |
||||||||||
|
можно записать: |
|||||||||||||||||||||
|
dUV,S |
n |
———∂U |
dMi |
n |
(15.30) |
||||||||||||||||
|
= Σ |
∂M |
i |
V,S,M |
= ΣϕidMi ; |
|||||||||||||||||
|
i = 1 |
j |
i = 1 |
|||||||||||||||||||
|
dHp,S |
n |
———∂H |
dMi |
n |
(15.31) |
||||||||||||||||
|
= Σ |
∂M |
i |
p,S,M |
= ΣϕidMi ; |
|||||||||||||||||
|
i = 1 |
j |
i = 1 |
|||||||||||||||||||
|
dFT,V |
n |
———∂F |
dMi |
n |
(15.32) |
||||||||||||||||
|
= Σ |
∂M |
i |
T,V,M |
= ΣϕidMi . |
|||||||||||||||||
|
i = 1 |
j |
i = 1 |
|||||||||||||||||||
Напомним, что в соответствии с уравнением (5.43)
ϕ= h – Ts.
Закон действующих масс. Константа равновесия. Рассмотрим случай гомогенной реакции, участниками которой являются газообразные вещества, обладающие свойствами идеальных газов. Если стехиометрические числа реагентов равны единице, то уравнение реакции имеет вид:
|
w |
+ A ′ + … |
|||
|
A |
+ A |
+ … L A′ |
(15.33) |
|
|
1 |
2 |
1 |
2 |
|
|
w1 |
С молекулярно-кинетической точки зрения скорость реакции пропорциональна числу столкновений молекул, а это последнее тем больше, чем выше концентрация веществ. Поэтому скорость протекания реакции слева направо
|
w = K [A1] [A2] …, |
(15.34) |
||||||
|
а скорость протекания реакции справа налево |
|||||||
|
w |
1 |
= K |
1 |
[A′ |
][A′ |
]… , |
(15.35) |
|
1 |
2 |
где [A1], [A2], …, [A′1 ], [A′2 ] … — концентрации реагентов, а K и K1 — кон-
станты скоростей реакций, зависящие от химической природы веществ, температуры, присутствия катализаторов и других факторов.
Уравнения (15.34) и (15.35) дают математическую форму з а к о н а д е й – с т в у ю щ и х м а с с , который может быть сформулирован следующим образом:
химическое действие вещества пропорционально его активной массе (в случае
|
гомогенной газовой реакции — концентрации). |
|||||||||
|
Очевидно, что при химическом равновесии w = w1 и, следовательно, |
|||||||||
|
K[A |
1 |
][A |
2 |
]… = K |
1 |
[A′ |
][A′ |
]… , |
(15.36) |
|
1 |
2 |
468

15.3. Константа равновесия и степень диссоциации
откуда
|
K1 |
[A1 |
][A2 |
]… |
(15.37) |
|
|
—– |
= —————————— = Kc ; |
||||
|
K |
[A′ |
][A |
′ |
]… |
|
|
1 |
2 |
||||
|
величина Kс называется к о н с т а н т о й |
р а в н о в е с и я |
и для данной идеально- |
газовой реакции зависит от температуры. Константа равновесия, определяемая либо экспериментально, либо расчетным путем, имеет огромное значение в химии.
Для более общего случая реакции (15.13)
|
ν |
+ ν |
w |
ν ′ A′ |
+ ν ′ A ′ + … |
|||||||||||||||
|
1 |
A |
1 |
2 |
A |
+ … L |
||||||||||||||
|
2 |
w1 |
1 |
1 |
2 |
2 |
||||||||||||||
|
значения скоростей реакций могут быть определены уравнениями |
|||||||||||||||||||
|
w = K [A |
1 |
]ν1 [A |
2 |
]ν2 … |
(15.38) |
||||||||||||||
|
и |
|||||||||||||||||||
|
ν ′ |
ν ′ |
||||||||||||||||||
|
w |
1 |
= K |
1 |
[A |
′ |
] |
1 [A′ ] |
2 … , |
(15.39) |
||||||||||
|
1 |
2 |
так как с молекулярно-кинетической точки зрения теперь уже существенны не только столкновения молекул различных веществ, но и столкновения молекул одного и того же вещества. Тогда для константы равновесия получаем:
|
[A1 ]ν1 [A1 |
]ν1 … |
||||||
|
Kc = ——————————————– |
ν1′ [A |
′]ν2′ |
. |
(15.40) |
|||
|
[A |
1 |
′] |
2 |
… |
|||
Последнее уравнение является универсальным. Для одних и тех же внешних условий величина Kс для данной реакции неизменна.
Если в объем, в котором происходит химическая реакция, добавить некоторое количество одного или нескольких реагентов или изменить температуру, то равновесие может быть нарушено. В этом случае возникший вновь химический процесс, направленный на восстановление нарушенного химического равновесия, следует правилу Л е – Ш а т е л ь е — Б р а у н а : каждое изменение одного из факторов равновесия вызывает превращение системы в таком направлении, что фактор, нарушивший равновесие, стремится к своему первоначальному значению. Если, например, увеличить температуру реагентов, то в соответствии с правилом Ле-Шателье—Брауна возникший химический процесс будет идти с поглощением теплоты. Если добавить в смесь некоторое количество одного из реагентов, то возможная реакция будет направлена в сторону уменьшения количества этого реагента.
Рассмотрим идеально-газовую реакцию, протекающую без изменения числа молей, например реакцию образования йодоводорода
Н2 + I2 L 2HI.
Обозначив число молей каждого реагента через Мi, мы можем для каждого из реагентов написать уравнение Клапейрона
|
pi |
M |
μRT = [Ai ]μRT , |
|
|
= —–i |
(15.41) |
||
|
V |
где [Ai] — число молей данного вещества в единице объема, т.е. мольная концентрация данного вещества. В этом случае
|
[H2 ][I2 |
] |
pH2 pI2 |
(μRT )2 |
pH2 pI2 |
Kp , |
(15.42) |
|
Kc = ——————— |
= ——————– |
——————– |
= ——————– = |
|||
|
[HI]2 |
pH2 I |
(μRT )2 |
pH2 I |
469

Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
где pH2 , pI2 , pHI — парциальные давления, а Kp — константа равновесия реак-
ции, выраженная через парциальные давления реагентов. Как видно из сказанного, в случае идеально-газовой реакции, протекающей без изменения числа молей, Kp = Kс .
Рассмотрим теперь наиболее общий случай — реакцию вида
ν1A1 + ν2A2 + … L ν1′ A1′ + ν2′ A2′ + …
|
при ν′ |
+ ν′ |
+ … – ν |
1 |
– ν |
2 |
– … |
= ν, где ν — изменение числа молей реаген- |
|
1 |
2 |
тов при протекании реакции слева направо. Так как мольная концентрация реагента может быть по-прежнему представлена в виде
|
pi |
(15.41а) |
|||||||||||||||||
|
[Ai] = ———- , |
||||||||||||||||||
|
μRT |
||||||||||||||||||
|
то |
||||||||||||||||||
|
ν |
1 |
ν |
2 … |
ν1 |
ν2 |
… |
||||||||||||
|
[A1 ] |
[A2 |
] |
pA1 |
pA2 |
ν |
, |
(15.42а) |
|||||||||||
|
Kc = —————————————— |
= ————————– (μRT) |
|||||||||||||||||
|
[A |
1 |
′]ν1′ |
[A |
2 |
′]ν2′ … |
pν1′ |
pν2′ |
… |
||||||||||
|
A′ |
A′ |
|||||||||||||||||
|
1 |
2 |
|||||||||||||||||
|
или |
||||||||||||||||||
|
K |
с |
= K |
p |
(μRT )Δν. |
(15.43) |
|||||||||||||
В практических расчетах газовых реакций часто используется константа равновесия Kр , так как состав смеси во многих случаях задается мольными долями
реагентов, которые пропорциональны парциальным давлениям. Следует иметь в виду, что в литературе можно встретить различные значения констант равновесия для одних и тех же реакций и для одних и тех же внешних условий. Дело в том, что иногда в выражениях для констант равновесия в числителе фигурируют произведения концентраций (или парциальных давлений) исходных продуктов в соответствующих степенях, а в знаменателе — те же произведения для продуктов реакций; так, в частности, поступили и мы. В некоторых же случаях берется обратное соотношение.
Диссоциация. В химии часто используется понятие диссоциации — частичного или полного распада вещества на его составные части. Например, реакция
2NO2 L N2O4,
протекающая справа налево, представляет собой диссоциацию N2O4.
Под степенью диссоциации α понимается отношение числа молей первоначально взятого вещества, распавшегося на продукты диссоциации, ко всему первоначальному количеству вещества в молях М0.
Следовательно, в состоянии равновесия общее число молей смеси М для при-
|
веденной выше реакции разложения N2O4 будет равно: |
|
|
М = (1 – α)М0 + 2αМ0 = (1 + α)М0, |
(15.44) |
где (1 – α)М0 — число молей N2O4; 2αM0 — число молей NO2.
Уравнение (15.44) справедливо для всех реакций, в результате которых 1 моль первоначально взятого вещества диссоциирует на 2 моля продуктов диссоциации.
Для того чтобы установить связь между константами равновесия и степенью диссоциации, выразим концентрации реагентов через степень диссоциации,
470

15.3. Константа равновесия и степень диссоциации
воспользовавшись снова примером разложения тетраксида азота. Из сказанного выше очевидно, что
|
(1 – α)M0 |
|
|
[N2O4] = ————————– |
|
|
V |
|
|
и |
|
|
2αM0 |
, |
|
[NO2] = ————– |
|
|
V |
где V — общий объем смеси. Следовательно,
|
K |
[NO2 ]2 |
4α2M02 |
V |
4α2 |
M0 |
|
|
c |
= —————— |
= —————– |
————————– |
= ————- |
—— . |
|
|
[N2O4 ] |
V 2 |
(1 – α)M0 |
1 – α V |
|||
Из уравнения Клапейрона
pV = M0(1 + α)μRT
получаем:
Подставляя выражение для
K c =
|
M0 |
p |
||||
|
—— |
= |
—————————— |
|||
|
V |
(1 + α)μRT . |
||||
|
M0 |
|||||
|
—— |
в уравнение (15.45), имеем: |
||||
|
V |
|||||
|
4α2 |
M0 |
4α2p |
1 |
||
|
————- |
—— |
————— |
———- |
||
|
1 – α |
V = |
1 – α |
2 |
μRT . |
|
Так как в соответствии с уравнением (15.43)
Kc = Kp(μRT)Δν
и в данном случае ν = –1, то
|
4 |
α2p |
|
Kр = ————— . |
|
|
1 |
– α2 |
(15.45)
(15.46)
(15.47)
(15.48)
(15.49)
Важно отметить, что в идеально-газовых реакциях рассмотренного типа (т.е. когда на 1 моль исходного продукта может быть получено 2 моля продуктов диссоциации) увеличение давления при постоянной температуре и, следовательно, при неизменных значениях Kc и Kp приводит, как видно из уравнения
(15.49), к уменьшению степени диссоциации α. Тот же результат можно получить и на основе правила Ле-Шателье—Брауна. Действительно, увеличение давления в системе должно, согласно этому правилу, вызвать процесс, в результате которого давление смеси вновь снизится. Но это может произойти только при уменьшении степени диссоциации, так как в этом случае уменьшается число молей смеси, что при постоянной температуре должно повлечь за собой уменьшение давления в системе.
Вид зависимости между Kp и α определяется характером реакции. Используя
приведенный выше метод, легко получить уравнения, дающие взаимосвязь между Kp и α для разных типов реакций. Ниже приведены соответствующие
уравнения для некоторых, имеющих важное значение реакций. 1. Реакция типа
|
X + X L X2, |
(15.50) |
|
уже рассмотренная нами выше, например 2NO2 L N2O4, |
2N L N2: |
|
4α2p |
|
|
Kp = ————— . |
|
|
1 – α2 |
471

Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
|
2. Реакция типа |
|||
|
X + Y L XY, |
(15.51) |
||
|
например NH3 + HCl L NH4C1, |
N + O L NO: |
||
|
α2p |
(15.52) |
||
|
Kp = ————— . |
|||
|
1 – α2 |
|||
|
3. Реакция типа |
|||
|
2XY + Х2 L 2X2Y, |
(15.53) |
||
|
например 2СО + О2 L 2СО2, |
2ОH + Н2 L 2Н2О, |
2Н2 + О2 L 2Н2О: |
|
|
Kp |
α3p |
(15.54) |
|
|
= —————————————- . |
|||
|
(1 – α)2 (2 + α) |
|||
|
4. Реакция типа |
|||
|
X2 + Y2 L 2XY, |
(15.55) |
||
|
например Cl2 + H2 L 2HCl, |
H2 + I2 L 2HI: |
||
|
Kp |
α2 |
(15.56) |
|
|
= Kc = ———————— . |
|||
|
4(1 – α2 ) |
|||
|
5. Реакция типа |
|||
|
A + X2 L AX2, |
(15.57) |
где A — символ химического вещества в твердом состоянии; в данном случае реакция является гетерогенной, концентрация твердого реагента рассматривается как величина постоянная и поэтому в уравнение константа равновесия не вводится. Примером подобной реакции является
С + О2 L СО2
|
K |
= K |
α |
(15.58) |
||
|
p |
c |
= ————- . |
|||
|
1 – α |
|||||
|
6. Реакция типа |
|||||
|
A + AX2 L 2AX, |
(15.59) |
||||
|
например С + СО2 L 2СО: |
|||||
|
Kp |
α(2 – α) |
(15.60) |
|||
|
= —————————- . |
|||||
|
4p(1 – α2 ) |
Диссоциация двухатомных газов. Для решения некоторых важных технических задач представляет особый интерес изучение термодинамических свойств диссоциирующих двухатомных газов (таких, в частности, как водород, кислород, азот и др.). При невысоких давлениях компоненты смеси (одноатомный и двухатомный газы) могут рассматриваться как идеальные газы. Константа равновесия Kp реакции диссоциации, уже рассмотренной нами выше,
определяется уравнением (15.49). Это уравнение может быть переписано в виде
|
α = |
Kp |
. |
(15.61) |
|
——————- |
Соотношения, с помощью которых вычисляется величина Kp, будут получены несколько ниже [см. уравнение (15.107)]. Вычислив значение Kp для различных р и
Т, с помощью уравнения (15.61) можно определить зависимость α непосредственно от давления и температуры и тем самым определить состав смеси.
472

15.3. Константа равновесия и степень диссоциации
Зная состав смеси, можно определить ее основные термодинамические свойства. Мольная энтальпия рассматриваемого диссоциирующего идеального газа определяется соотношением
|
Hсм = N1H1 + N2H2, |
(15.62) |
где H1 и H2 — мольные энтальпии компонентов смеси (соответственно одноатомного и двухатомного газа) в идеально-газовом состоянии, a N1 и N2 — мольные доли компонентов смеси. Напомним, что мольная доля Ni компонента смеси определяется уравнением (1.39)
Mi
Ni = —– ,
M
где Mi и М — числа молей соответственно i-го компонента смеси и всей смеси.
Поскольку, как показано выше для аналогичной реакции [уравнение (15.44)], M1 = (1 – α)М0 , М2 = 2αМ0 и М = (1 + α) М0, где М0 — первоначальное
(до начала диссоциации) количество вещества в молях, то очевидно, что
|
N1 |
1 – α |
и N2 |
2α |
(15.63) |
|
= ————- |
= ————- . |
|||
|
1 + α |
1 + α |
В соответствии с уравнениями (1.50) и (1.55) кажущаяся молекулярная масса
|
рассматриваемой смеси одноатомного и двухатомного газов равна: |
|
|
μсм = N1μ1 + N2μ2. |
(15.64) |
|
Учитывая (15.63) и имея в виду, что |
|
|
μ2 = 2μ1 |
(15.65) |
(молекула диссоциирует на два атома), получаем из (15.64) для рассматриваемой смеси:
|
μсм |
2μ1 |
(15.66) |
|
= ————- . |
||
|
1 + α |
Тепловой эффект изобарно-изотермической реакции диссоциации (так называемая теплота диссоциации Qдиссp ) определяется очевидным соотношением
|
Qpдисс = 2H1 – H2 . |
(15.67) |
С учетом (15.63), (15.66) и (15.67) получаем из (15.62) следующее соотношение
|
Hсм |
рассматриваемого диссоциирующего газа: |
||||||||
|
для удельной энтальпии hсм |
= ——– |
||||||||
|
μсм |
|||||||||
|
H |
1 – α |
Q |
дисс |
||||||
|
1 |
– ————- |
p |
1 – α |
||||||
|
2 |
= |
h1 |
дисс |
(15.68) |
|||||
|
hсм = —————————————— |
– ————- |
Qp . |
|||||||
|
μ1 |
2μ1 |
Дифференцируя величину hсм по температуре при T = const и учитывая, что в соответствии с законом Кирхгофа
|
dQpдисс |
= 2μc |
– μc |
, |
(15.69) |
|||||||
|
————— |
p1 |
p |
|||||||||
|
dT |
2 |
||||||||||
|
получаем из (15.68) для теплоемкости ср диссоциирующего газа: |
|||||||||||
|
c |
см |
= αc |
+ (1 – α)c |
Qpдисс |
∂α |
. |
(15.70) |
||||
|
p2 |
+ ———— |
—— |
|||||||||
|
p |
p1 |
2μ |
1 |
∂T |
|||||||
|
p |
473

Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
В уравнении (15.69) в отличие от уравнения закона Кирхгофа (15.15) фигурируют мольные теплоемкости, потому что, как видно из (15.67), здесь Qдиссp —
мольная теплота диссоциации.
Как видно из соотношения (15.70), теплоемкость сp рассматриваемой нами химически реагирующей смеси отличается от теплоемкости сp смеси нереагирующих идеальных газов на величину последнего слагаемого правой части уравнения (15.70) — так называемого химического вклада в теплоемкость. Неучет химического вклада может привести к грубым ошибкам при расчете теплоемкости такой смеси.
Поскольку на графике α = f (p, T ) изобары имеют перегиб (это видно, например, из рис. 15.4), очевидно, что в точке этого перегиба фигурирующая в уравнении (15.70) величина (∂α ⁄ ∂T )p проходит через максимум. Понятно, что в
той области температур, где эта величина имеет максимум, процесс диссоциации проходит наиболее интенсивно. Соответственно в этой области температур имеют перегиб изобары в h, T-диаграмме диссоциирующего газа и согласно уравнению (15.70) имеют максимумы изобары теплоемкости ср.
Как отмечалось выше, при невысоких давлениях диссоциирующий газ можно рассматривать как смесь химически реагирующих идеальных газов. Следует подчеркнуть, что хотя каждая из составляющих смеси представляет собой в этом случае идеальный газ (у которого, в частности, энтальпия и теплоемкость не зависят от давления), вся система в целом ведет себя подобно реальному газу (в частности, энтальпия и теплоемкость ср смеси оказываются зависящими от давления). Очевидно, что «степень неидеальности» такой смеси тем больше, чем больше тепловой эффект реакции диссоциации. Наличие некоторых реальных свойств у смеси реагирующих идеальных газов не вызывает удивления, поскольку имеет место определенная аналогия между такой системой и реальным газом — существует известное сходство между диссоциацией молекул и распадом межмолекулярных комплексов (ассоциаций).
Степень диссоциации и ионизации ,%
100
90
80
70
60
50
40
30
20
10
0
|
10-2 |
|
|
10-4 |
|
|
10-3 |
Диссоциация |
|
при p=1MПа |
|
|
10-1 |
Ионизация при p=10-1кПа
100
101 102
103
|
2000 |
4000 |
6000 |
8000 |
10000 |
|
Температура T, K |
Рис. 15.4
474

15.3. Константа равновесия и степень диссоциации
Термическая ионизация. Уравнение Саха. В современных высокотемпературных установках и аппаратах все чаще приходится иметь дело с веществами в так называемом плазменном состоянии.
При высоких температурах в одноатомном газе происходит процесс термической ионизации — отрыва электронов с внешней электронной оболочки атома. В результате этого процесса образуется смесь отрицательно заряженных электронов, положительно заряженных ионов и электрически нейтральных атомов. Эта смесь электрически заряженных и нейтральных частиц, как уже отмечалось в гл. 12, является электропроводной. Состав этой смеси определяется давлением и температурой смеси.
Следует отметить, что термическую ионизацию можно рассматривать как химическую реакцию. Так, уравнение реакции однократной ионизации 1) (отрыв от атома одного электрона) может быть записано в следующем виде:
где символом А обозначен нейтральный атом; е — свободный электрон и A+ — положительно заряженный ион. Как и любая другая химическая реакция, эта реакция идет в обоих направлениях. Процесс, обратный ионизации, — образование электрически нейтрального атома при соединении иона и электрона — называют рекомбинацией.
Реакция ионизации характеризуется степенью ионизации, понятие о которой вводится аналогично понятию степени диссоциации для реакции диссоциации. Степенью однократной ионизации α называют отношение числа молей первоначально взятого нейтрального газа, распавшегося на продукты ионизации (ионы и электроны), ко всему первоначальному количеству молей нейтрального газа.
Уравнение для зависимости степени однократной ионизации одноатомного газа от константы равновесия Kp (при невысоких давлениях, когда плазма может
рассматриваться как идеальный газ) может быть получено обычным путем с помощью закона действующих масс.
Понятно, что для рассматриваемой реакции однократной ионизации (15.71) в
|
состоянии равновесия общее число молей смеси будет равно: |
|
|
М = (1 – α) М0 + αМ0 + αМ0 = (1 + α) М0 , |
(15.72) |
где (1 – α)М0 — число молей нейтрального газа; М0 — число молей ионов, равное числу молей свободных электронов.
Мольные концентрации реагентов реакции однократной ионизации (15.71) определяются следующими очевидными соотношениями:
|
(1 – α)M0 |
+ |
αM0 |
|||
|
[А] = |
————————– |
и [А ] + [е] = |
———– |
, |
(15.73) |
|
V |
V |
где V — общий объем плазмы.
Из уравнения Клапейрона для рассматриваемой смеси в состоянии равновесия
|
pV = (1 + α)М0μRT |
(15.74) |
|||
|
получаем: |
||||
|
M0 |
p |
1 |
||
|
—— |
= |
————- |
———- |
(15.75) |
|
V |
1 + α |
μRT . |
1) Процесс отрыва второго электрона (двукратная ионизация) начинается практически лишь при тех температурах, при которых уже закончилась однократная ионизация (т.е. все атомы ионизированы). Эта температура обычно весьма высока; например, у аргона однократная ионизация заканчивается при температурах порядка 20 000 К. Отрыв последующих электронов происходит при еще более высоких температурах.
475

Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
В соответствии с уравнениями (15.40) и (15.73) выражение для константы
|
равновесия Kс реакции ионизации запишется следующим образом: |
|||||||||
|
K |
[A] |
1 – α |
V |
(15.76) |
|||||
|
c |
= ——————- = |
————- |
—— , |
||||||
|
[A |
+ |
][e] |
α |
2 |
M |
0 |
|||
|
откуда с учетом (15.75) |
|||||||||
|
1 – α2 |
μRT . |
(15.77) |
|||||||
|
Kc = ————— |
|||||||||
|
α2p |
Величина изменения числа молей реагентов при протекании реакции (15.71) слева направо, ν = ν1′ + ν2′ + … – ν1 – ν2 – … , в случае рассматриваемой
реакции (ν1 = 1; ν1′ =1; ν2′ =1) будет равно Δν = 1. В этом случае из уравнения (15.43) следует:
|
Kp |
Kc |
(15.78) |
|
|
= ———- . |
|||
|
μRT |
|||
|
Из (15.77) и (15.78) очевидно, что для реакции ионизации |
|||
|
1 – α2 |
(15.79) |
||
|
Kp = ————— |
|||
|
α2p |
|||
|
и, следовательно, |
|||
|
α |
1 |
(15.80) |
|
|
= ————————– ; |

такова зависимость степени ионизации от константы Kp этой реакции. Вычислив значение Kp (как уже упоминалось, соотношения для расчета K p будут
приведены ниже), уравнение (15.80) можно преобразовать к виду α = f (р, Т). Как показывает расчет, в этом случае уравнение (15.80) приобретает следующий вид:
|
α2 |
5 ⁄ 2 |
Ui |
|||
|
– —– |
|||||
|
————— |
p = CT |
e |
kT |
; |
(15.81) |
|
1 – α2 |
здесь Ui — энергия ионизации данного газа (т.е., иными словами, тепловой
эффект реакции ионизации); k — постоянная Больцмана; С — константа. Уравнение (15.81) для зависимости степени однократной ионизации α от температуры и давления носит название у р а в н е н и я С а х а (по имени индийского астрофизика М. Саха, получившего это уравнение в 1920 г.).
Значение константы С не может быть определено термодинамическим путем; эта величина, вычисляемая методами статистической физики, оказывается равной:
|
C = |
ZiZe |
2πme 3 ⁄ 2 |
k |
5 ⁄ 2 |
, |
(15.82) |
|
|
———- |
————- |
||||||
|
Za |
h2 |
||||||
|
где те — масса электрона; h — постоянная Планка (h = 6,626æ10–27 |
эрг æс = |
= 6,626æ10–34 Дж), Zi, Ze и Za — так называемые статистические суммы по состояниям соответственно для ионов, электронов и нейтральных атомов (Ze = 2, а величины Zi и Za подсчитываются более сложным путем). Следует подчеркнуть,
что величина С является постоянной в том случае, если пренебречь зависимостью теплоемкости компонентов реагирующей смеси от температуры. При более точ-
476

Рис. 15.5
15.3. Константа равновесия и степень диссоциации
|
ном расчете с учетом этой зависимости вели- |
cp, cv, к Дж§—кгæK˜ |
||||||
|
чина С оказывается зависящей от темпера- |
10 |
||||||
|
туры [в уравнении (15.82) в |
этом случае |
8 |
|||||
|
зависят от температуры величины Zi и Za ]. |
|||||||
|
Характер зависимости степени иониза- |
6 |
||||||
|
ции α от температуры и давления иллюстри- |
cp |
||||||
|
руется графиком на рис. 15.4, где (в правой |
4 |
||||||
|
части графика) приведены значения α для |
2 |
cv |
|||||
|
водяного пара (сплошные линии) и водорода |
|||||||
|
(пунктир) на разных изобарах. Как видно из |
|||||||
|
этого графика, на котором нанесены также |
0 |
5000 |
10 000 |
T, K |
|||
|
кривые зависимости степени |
диссоциации |
от р и Т, ионизация на соответствующих изобарах начинается практически лишь при
тех температурах, при которых уже заканчивается диссоциация газа (т.е. газ становится полностью диссоциированным).
Аналогично тому, как это имеет место при диссоциации, в случае ионизации в той области температур, где диссоциация происходит наиболее интенсивно [т.e. в районе перегиба изобары α = f (pT ), где, следовательно, величина (∂α ⁄ ∂T)p проходит через максимум], теплоемкость плазмы проходит через
максимум.
Таким образом, при повышении температуры газа его теплоемкость вначале проходит через максимум, обусловленный диссоциацией, а затем через максимум, обусловленный однократной ионизацией 1). На рис. 15.5 приведен график зависимости теплоемкостей сp и сv воздуха от температуры (при стандартной
плотности), на котором видны диссоциационные и ионизационные максимумы теплоемкости.
Расчет термодинамических свойств плазмы (для однократной термической ионизации при невысоких давлениях) производится по уравнению состояния (15.74), в котором значение α определяется с помощью уравнения Саха. Определение свойств плазмы при высоких давлениях (так называемой плотной плазмы) является значительно более сложной задачей.
Выше было установлено, что химическое равновесие характеризуется двумя факторами: минимумом соответствующей характеристической функции и константой равновесия. Мы рассмотрели оба названных критерия равновесия независимо друг от друга, но можно предполагать, что между ними существует вполне определенная связь.
Метод Вант-Гоффа. Для выявления взаимосвязи между этими двумя важнейшими факторами равновесия воспользуемся методом, предложенным голландским химиком Я. Вант-Гоффом, на примере идеально-газовой, термодинамически обратимой реакции:
2Н2 + О2 L 2Н2О.
Представим себе следующую схему (рис. 15.6). В сосудах А, В и D находятся чистые вещества Н2, О2 и Н2О при давлениях соответственно PH2 , PO2 и PH2O
c концентрациями cH2 , cO2 и cH2O . Эти давления и концентрации в общем случае являются неравновесными в отношении рассматриваемой реакции.
1) Ионизация более высоких порядков также приводит к появлению максимумов теплоемкости.
477
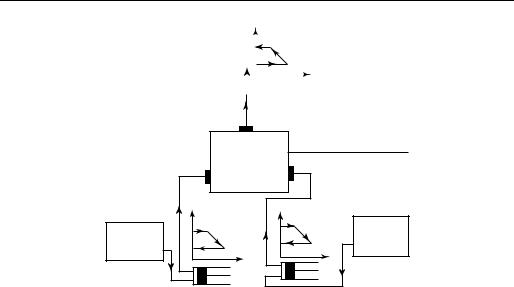
Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
|
D |
p |
|||||||||
|
H |
O |
1 PH |
O |
|||||||
|
2 |
2 |
dT=0 |
||||||||
|
III |
||||||||||
|
cH2O PH2O |
2 pH2O |
|||||||||
|
v |
||||||||||
|
d |
||||||||||||||
|
2H2+ O2L2H2O |
Ящик Вант-Гоффа |
|||||||||||||
|
a |
[H2][O2][H2O] |
b |
||||||||||||
|
pH2 pO2 |
pH2O |
|||||||||||||
|
A |
p |
1 PH |
p |
1 PO2 |
B |
|||||||||
|
2 |
O2 |
|||||||||||||
|
H |
2 |
I |
II |
pO2 |
cO2 |
PO2 |
||||||||
|
pH |
||||||||||||||
|
cH |
2 |
PH |
2 |
2 |
2 |
|||||||||
|
2 |
v |
v |
||||||||||||
Рис. 15.6
Кроме того, имеется сосуд с полупроницаемыми перегородками, именуемый иногда ящиком (сосудом) Вант-Гоффа. Полупроницаемая перегородка а пропускает только водород, перегородка b — только кислород и перегородка d — только водяной пар. В сосуде Вант-Гоффа водород, кислород и водяной пар находятся в состоянии равновесия с соответствующими равновесными давлениями PH2 , PO2 и PH2O и концентрациями [Н2], [О2] и [Н2О].
Если, не нарушая равновесия в сосуде Вант-Гоффа, вводить в него весьма малыми порциями при параметрах, соответствующих параметрам компонентов смеси, Н2 и О2 и выводить Н2О, то можно представить себе термодинамически
обратимую реакцию. В схеме необходимо предусмотреть три цилиндра с поршнями, с помощью которых производится обратимое сжатие (или расширение) составляющих реакции.
Представим себе следующий термодинамически обратимый интегральный процесс, осуществляемый при постоянной температуре и неизменном объеме системы. В ящик Вант-Гоффа обратимо (мелкими порциями) вводятся 2 моля Н2 и 1 моль О2, и из него выводится 2 моля Н2О. Объемы сосудов A, В и D
выбраны достаточно большими, чтобы неравновесные давления и концентрации газов в них рассматривать постоянными. Это условие, однако, не является обязательным и вводится лишь для упрощения последующих рассуждений.
Очевидно, что при этом необходимо провести обратимое изотермическое расширение двух молей Н2 и одного моля О2 от начальных давлений PH2 и PO2
до конечных pH2 и pO2 и сжатие двух молей Н2О от PH2O до pH2O . В результате
будет получена работа L, равная алгебраической сумме трех работ, соответствующих трем названным процессам, и представляющая собой максимальную работу (все процессы термодинамически обратимы!), в которую не входит работа против внешнего давления (суммарный объем системы остается неизменным, а поршни возвращаются в исходное положение!), обозначаемая нами LV, T и равная уменьшению свободной энергии системы.
478

15.3. Константа равновесия и степень диссоциации
|
Следовательно, |
||||
|
LV, T = ΣL = LI + LII + LIII, |
(15.83) |
|||
|
где (см. рис. 15.6) |
PH2 |
|||
|
2 |
1 |
|||
|
LI = – ∫V dp = ∫V dp = 2μRT ln ——– . |
(15.84) |
|||
|
1 |
2 |
pH |
2 |
|
Поскольку давления пропорциональны концентрациям, то
|
LI |
cH2 |
= |
μRT ln |
cH2 2 |
|||||||||||||||||||||||||
|
= 2μRT ln ———- |
————- . |
||||||||||||||||||||||||||||
|
[H2 |
] |
[H2 ] |
2 |
||||||||||||||||||||||||||
|
Аналогичным путем нетрудно получить: |
|||||||||||||||||||||||||||||
|
LII |
PO2 |
μRT ln |
cO2 |
||||||||||||||||||||||||||
|
= |
μRT ln ——– = |
———- |
; |
||||||||||||||||||||||||||
|
pO |
2 |
[O2 ] |
|||||||||||||||||||||||||||
|
LIII |
= |
– 2μRT ln |
PH2O |
– |
cH2 2O |
||||||||||||||||||||||||
|
———— = |
μRT ln —————— . |
||||||||||||||||||||||||||||
|
pH2O |
[H2 O]2 |
||||||||||||||||||||||||||||
|
Таким образом, |
|||||||||||||||||||||||||||||
|
LV, T = LI + LII |
LIII |
cH2 |
2 |
cO2 |
cH2 |
2 O |
|||||||||||||||||||||||
|
+ |
= μRT ln |
————- |
+ ln |
———- |
– |
ln —————– = |
|||||||||||||||||||||||
|
[H |
2 |
]2 |
[O2 ] |
[H |
2 |
O]2 |
|||||||||||||||||||||||
|
cH2 cO |
[H2O]2 |
cH2 cO |
2 |
[H |
2 |
]2 [O |
2 |
] |
|||||||||||||||||||||
|
2 |
2 |
= μRT |
ln |
2 |
ln |
||||||||||||||||||||||||
|
= μRT ln ————————————- |
————— – |
————————- . |
|||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
||||||||||||||||||||||||||
|
cH2O [H2 ] |
[O2 ] |
cH2O |
[H2O] |
||||||||||||||||||||||||||
|
Далее, поскольку в соответствии с уравнением (15.40) |
|||||||||||||||||||||||||||||
|
[H2 ]2[O2 |
] |
||||||||||||||||||||||||||||
|
K c = ————————- , |
|||||||||||||||||||||||||||||
|
[H |
2 |
O]2 |
|||||||||||||||||||||||||||
|
уравнение (15.88) может быть записано в следующем виде: |
|||||||||||||||||||||||||||||
|
c2 |
c |
O |
|||||||||||||||||||||||||||
|
L |
= μRT ln |
H |
2 |
2 |
– ln K . |
||||||||||||||||||||||||
|
V, T |
————— |
||||||||||||||||||||||||||||
|
2 |
c |
||||||||||||||||||||||||||||
|
cH2O |
(15.85)
(15.86)
(15.87)
(15.88)
(15.89)
Важно отметить, что на основании сделанных рассуждений можно заключить независимо от молекулярно-кинетических представлений о скорости реакции, что значение
|
K c |
[H2 ]2[O2 ] |
|
|
= ————————- |
O]2 |
|
|
[H |
||
|
2 |
для данной реакции и заданных условий ее протекания постоянно, так как работа, полученная в обратимом процессе для заданных условий, всегда постоянна.
479

Глава 15 . ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
|
Для общего случая химической реакции |
|||||||||||||||||||||
|
ν |
1 |
A |
1 |
+ ν |
2 |
A |
2 |
+ … L ν′ A′ + ν′ A ′ + … |
|||||||||||||
|
1 |
1 |
2 |
2 |
||||||||||||||||||
|
уравнение (15.89) можно написать в виде |
|||||||||||||||||||||
|
cν1 c |
ν2 … |
||||||||||||||||||||
|
LV, T = |
μRT |
A1 |
A2 |
ln Kc |
, |
(15.90) |
|||||||||||||||
|
ln ———————— – |
|||||||||||||||||||||
|
cν1′ cν2′ |
… |
||||||||||||||||||||
|
A′ |
A′ |
||||||||||||||||||||
|
или, что то же самое, |
1 |
2 |
|||||||||||||||||||
|
m |
|||||||||||||||||||||
|
LV, T = μRT |
∑ (νi ln ci ) – ln Kc |
, |
(15.91) |
||||||||||||||||||
|
i = 1 |
|||||||||||||||||||||
|
где |
|||||||||||||||||||||
|
m |
+ … – ν1′ ln c |
– ν2′ ln c |
|||||||||||||||||||
|
∑ νi ln ci = ν1 ln cA |
+ ν2 |
ln cA |
′ |
′ – … |
(15.92) |
||||||||||||||||
|
1 |
2 |
A1 |
A2 |
i = 1
Уравнение (15.91) может быть преобразовано и константа равновесия Kс заменена константой Kp. Из уравнения Клапейрона
piV = MiμRT,
где Mi — число молей данного вещества, получаем:
|
ci |
Mi |
pi |
(15.93) |
|
= —– |
= ———- . |
||
|
V |
μRT |
Следовательно, выражение (15.92) можно представить в виде
|
ν1 |
ν2 |
… |
||||||||||||||||||||||||
|
m |
ln |
ci = |
ln |
cA1 cA2 |
= |
|||||||||||||||||||||
|
∑ νi |
————————- |
|||||||||||||||||||||||||
|
c |
ν1′ |
ν |
2′ |
… |
||||||||||||||||||||||
|
i = 1 |
′ |
c |
′ |
|||||||||||||||||||||||
|
A |
1 |
A |
2 |
|||||||||||||||||||||||
|
Pν1 Pν2 … |
′ |
′ |
||||||||||||||||||||||||
|
+ … – ν1 |
||||||||||||||||||||||||||
|
– ν2 |
– … |
|||||||||||||||||||||||||
|
= ln |
A1 |
A2 |
ν1 |
+ ν2 |
= |
|||||||||||||||||||||
|
————————– (μRT) |
||||||||||||||||||||||||||
|
Pν1′Pν2′ |
… |
|||||||||||||||||||||||||
|
A′ |
A′ |
|||||||||||||||||||||||||
|
1 |
2 |
Pν1 Pν2 … |
||||||||||||||||||||||||
|
= |
ln |
A1 |
A2 |
+ ln |
(μRT) |
ν |
, |
(15.94) |
||||||||||||||||||
|
————————– |
||||||||||||||||||||||||||
|
Pν1′Pν2′ |
… |
|||||||||||||||||||||||||
|
A |
′ |
A′ |
||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||
|
где |
||||||||||||||||||||||||||
|
ν = ν′ |
+ |
ν′ |
+ … |
– ν |
1 |
– ν |
2 |
– … |
||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||
|
Но так как согласно (15.43) |
||||||||||||||||||||||||||
|
K |
с |
= K |
(μRT )Δν, |
|||||||||||||||||||||||
|
p |
480

15.3. Константа равновесия и степень диссоциации
то
|
m |
||||||||||
|
LV, T = μRT |
∑ νi ln ci – ln Kc |
= |
||||||||
|
i = 1 |
||||||||||
|
ln Pν1 Pν2 … |
||||||||||
|
= μRT |
A1 |
A2 |
ν |
– ln Kc |
. |
|||||
|
——————————– + ln (μRT) |
||||||||||
|
ln Pν1′Pν2′ |
… |
|||||||||
|
A′ |
A′ |
|||||||||
|
1 |
2 |
Принимая во внимание, что, как это следует из (15.43),
ln Kp = ln Kс – ln (μ RT )Δν,
получаем из (15.95):
m
LV, T = μRT ∑ νi ln Pi – ln Kp .
i = 1
Уравнения (15.91) и (15.96), дающие зависимость между максимальной работой изохорно-изотермического процесса LV, T и константами равновесия Kс и Kp,
имеют большое значение. Однако для практических расчетов наибольший интерес представляют соотношения для изобарно-изотермического процесса. Эти соотношения легко могут быть получены.
Для того чтобы представить себе обратимую изобарно-изотермическую реакцию, сосуды А, В и D (рис. 15.6) нужно было бы снабдить поршнями, превратив их в емкости не постоянного объема, а постоянного давления. В этом случае уравнения для LI, LII и LIII необходимо было бы дополнить слагаемыми,
учитывающими работу, связанную с изменением объема сосудов А, В и D. Иными словами, для изобарно-изотермического процесса
|
L |
cH2 |
2 |
+ P |
V |
; |
(15.97) |
||||||
|
I |
= μRT ln ————- |
H2 |
||||||||||
|
[H |
2 |
]2 |
A |
|||||||||
|
LII |
cO2 |
PO2 |
VB ; |
|||||||||
|
= μRT ln ———- |
+ |
(15.98) |
||||||||||
|
[O2 ] |
||||||||||||
|
L |
= |
cH2 2O |
+ |
P |
V , |
(15.99) |
||||||
|
III |
– μRT ln —————— |
H |
2O |
|||||||||
|
[H |
2 |
O]2 |
D |
|||||||||
где VA , VB и VD — изменения объемов сосудов А, В, и D.
Но величина Lp, T равна, как известно, работе обратимого изобарно-изотерми-
|
ческого процесса за вычетом работы против внешнего давления, т.е. |
||||||||||
|
Lp, T = LI + LII + LIII |
– ∑p V . |
(15.100) |
||||||||
|
Для данного примера |
||||||||||
|
∑p |
V = PH |
2 |
VA + PO |
2 |
VB + PH |
O VD, |
(15.101) |
|||
|
2 |
||||||||||
|
и поэтому в общем случае |
||||||||||
|
m |
||||||||||
|
Lp, |
T = μRT |
∑ (νi ln ci ) – ln Kc |
(15.102) |
i = 1
481
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



Связь между константой равновесия и степенью диссоциации
- Соотношение между константой равновесия и степенью диссоциации имеет различные формы для каждой реакции. Рассмотрим основные виды реакций, протекающих в процессе горения. 1. Реакция горения, возникающая при уменьшении количества молей. Эти реакции включают реакцию горения того же типа водорода и монооксида углерода. 2На+Оа2НаО2СО+Оа2СОа. Рассмотрим сжигание водорода reaction.
Определенная температура реакции, при которой известно значение равновесного KP, если i-й моль не реагировал при равновесии, то вместо 2 (1-а) молей пара в продукте сгорания остается только 2 (1-а) моля, вместо 2a. So, состав продуктов сгорания при равновесии выглядит следующим образом: Формула смеси газов (1.32) и (1.33) используется для определения парциального давления компонента Зная парциальное давление, находим константу равновесия по формуле (19.8 (2 + a) ’(2+ x p ’ 4(1-a)’ (2 + a) (1-a)! (19.12) Это уравнение показывает связь между константой равновесия и степенью диссоциации.
Дифференцируя это уравнение дважды и полагая, что у — 0, приходим к следующему уравнению для коэффициента с: Коэффициенты а, Ь и с!
Людмила Фирмаль
Постоянная равновесия определенной температуры имеет определенное
значение, поэтому степень диссоциации определяется давлением, при
котором происходит диссоциация occurs. To уточните этот эффект в правой
части уравнения (19.12), добавьте числитель и знаменатель к А3 К» = р. T
= cfs(и по мере увеличения давления степень диссоциации уменьшается.
То есть увеличивается целостность горения, увеличивается количество
образующегося водяного пара, увеличивается количество водорода
и кислорода decreases. In в этом случае равновесие, как говорят,
смещается вправо. 2.Газовая реакция реакция, которая происходит без
изменения количества молей участников.
- Эти реакции включают реакцию водных газов Ко + НАО Коа + на. Константа равновесия этой реакции определяется по формуле _ , «РСО, рН. Рассматривая эту реакцию, можно увидеть следующее: Если степень диссоциации равна а, то к моменту равновесия смесь не имеет ни 1 моля и ни одного моля, только (1-å) моль, но остается моль со и НАО, которые не могли бы реагировать из-за dissociation. So, составляющее парциальное давление в равновесии с составом смеси будет: Найти константу равновесия (19 13) Степень диссоциации в этом типе реакции не зависит от давления, так как давление, с которым происходит реакция, не входит в эту зависимость.
При высоких скоростях во избежание сильного повышения сопротивления потоку поверхность плиты надо обрабатывать с особой тщательностью.
Людмила Фирмаль
Если рассматривать уравнение зависимости между константой равновесия
и степенью диссоциации, то константа равновесия является гораздо более
удобным расчетным значением, чем степень диссоциации, и поэтому、 Продукт
сгорания принимает ровно константу равновесия, для которой дана таблица
значений в зависимости от температуры различных reactions.
Смотрите также:
- Решение задач по теплотехнике
Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.
Степень диссоциации
Классификация электролитов
Диссоциация электролитов
Константа диссоциации
Примеры решения задач
Задачи для самостоятельного решения
Степень диссоциации
Вещества, которые в растворах или расплавах полностью или частично распадаются на ионы, называются электролитами.
Степень диссоциации α — это отношение числа молекул, распавшихся на ионы N′ к общему числу растворенных молекул N:
α = N′/N
Степень диссоциации выражают в процентах или в долях единицы. Если α =0, то диссоциация отсутствует и вещество не является электролитом. В случае если α =1, то электролит полностью распадается на ионы.
Классификация электролитов
Согласно современным представлениям теории растворов все электролиты делятся на два класса: ассоциированные (слабые) и неассоциированные (сильные). Неассоциированные электролиты в разбавленных растворах практически полностью диссоциированы на ионы. Для этого класса электролитов a близко к единице (к 100 %). Неассоциированными электролитами являются, например, HCl, NaOH, K2SO4 в разбавленных водных растворах.
Ассоциированные электролиты подразделяются на три типа:
-
-
- Слабые электролиты существуют в растворах как в виде ионов, так и в виде недиссоциированных молекул. Примерами ассоциированных электролитов этой группы являются, в частности, Н2S, Н2SO3, СН3СOОН в водных растворах.
- Ионные ассоциатыобразуются в растворах путем ассоциации простых ионов за счет электростатического взаимодействия. Ионные ассоциаты возникают в концентрированных растворах хорошо растворимых электролитов. В результате в растворе находятся как простые ионы, так и ионные ассоциаты. Например, в концентрированном водном растворе КCl образуются простые ионы К+, Cl— , а также возможно образование ионных пар (К+Cl— ), ионных тройников (K2Cl+, KCl2— ) и ионных квадруполей (K2Cl2, KCl32- , K3Cl2+).
- Комплексные соединения(как ионные, так и молекулярные), внутренняя сфера которых ступенчато диссоциирует на ионные и (или) молекулярные частицы.
Примеры комплексных ионов: [Cu(NH3)4]2+, [Fe(CN)6]3+, [Cr(H2O)3Cl2]+.
-
При таком подходе один и тот же электролит может относиться к различным типам в зависимости от концентрации раствора, вида растворителя и температуры. Подтверждением этому являются данные, приведенные в таблице.
Таблица. Характеристика растворов KI в различных растворителях
| Концентрация электролита, С, моль/л | Температура
t,оС |
Растворитель | Тип электролита |
| 0,01 | 25 | Н2О | Неассоциированный (сильный) |
| 5 | 25 | Н2О | Ионный ассоциат |
| 0,001 | 25 | С6Н6 | Ассоциированный (слабый) |
Приближенно, для качественных рассуждений можно пользоваться устаревшим делением электролитов на сильные и слабые. Выделение группы электролитов “средней силы” не имеет смысла. Эти электролиты являются ассоциированными. К слабым электролитам обычно относят электролиты, степень диссоцииации которых мала α<<1.
Таким образом, к сильным электролитам относятся разбавленные водные растворы почти всех хорошо растворимых в воде солей, многие разбавленные водные растворы минеральных кислот (НСl, HBr, НNО3, НСlO4 и др.), разбавленные водные растворы гидроксидов щелочных металлов. К слабым электролитам принадлежат все органические кислоты в водных растворах, некоторые водные растворы неорганических кислот, например, H2S, HCN, H2CO3, HNO2, HСlO и др. К слабым электролитам относится и вода.
Диссоциация электролитов
Уравнение реакции диссоциации сильного электролита можно представить следующим образом. Между правой и левой частями уравнения реакции диссоциации сильного электролита ставится стрелка или знак равенства:
HCl → H+ + Cl—
Na2SO3 = 2Na+ + SO32-
Допускается также ставить знак обратимости, однако в этом случае указывается направление, в котором смещается равновесие диссоциации, или указывается, что α≈1. Например:
NaOH → Na+ + OH—
Диссоциация кислых и основных солей в разбавленных водных растворах протекает следующим образом:
NaHSO3 → Na+ + HSO3—
Анион кислой соли будет диссоциировать в незначительной степени, поскольку является ассоциированным электролитом:
HSO3— → H+ + SO32-
Аналогичным образом происходит диссоциация основных солей:
Mg(OH)Cl → MgOH+ + Cl—
Катион основной соли подвергается дальнейшей диссоциации как слабый электролит:
MgOH+ → Mg2+ + OH—
Двойные соли в разбавленных водных растворах рассматриваются как неассоциированные электролиты:
KAl(SO4)2 → K+ + Al3+ + 2SO42-
Комплексные соединения в разбавленных водных растворах практически полностью диссоциируют на внешнюю и внутреннюю сферы:
K3[Fe(CN)6] → 3K+ + [Fe(CN)6]3-
В свою очередь, комплексный ион в незначительной степени подвергается дальнейшей диссоциации:
[Fe(CN)6]3- → Fe3+ + 6CN—
Константа диссоциации
При растворении слабого электролита КА в растворе установится равновесие:
КА ↔ К+ + А—
которое количественно описывается величиной константы равновесия Кд, называемой константой диссоциации:
Kд = [К+] · [А—] /[КА] (2)
Константа диссоциации характеризует способность электролита диссоциировать на ионы. Чем больше константа диссоциации, тем больше ионов в растворе слабого электролита. Например, в растворе азотистой кислоты HNO2 ионов Н+ больше, чем в растворе синильной кислоты HCN, поскольку К(HNO2) = 4,6·10— 4, а К(HCN) = 4,9·10— 10.
Для слабых I-I электролитов (HCN, HNO2, CH3COOH) величина константы диссоциации Кд связана со степенью диссоциации α и концентрацией электролита c уравнением Оствальда:
Кд = (α2·с)/(1-α) (3)
Для практических расчетов при условии, что α<<1 используется приближенное уравнение:
Кд = α2·с (4)
Поскольку процесс диссоциации слабого электролита обратим, то к нему применим принцип Ле Шателье. В частности, добавление CH3COONa к водному раствору CH3COOH вызовет подавление собственной диссоциации уксусной кислоты и уменьшение концентрации протонов. Таким образом, добавление в раствор ассоциированного электролита веществ, содержащих одноименные ионы, уменьшает его степень диссоциации.
Следует отметить, что константа диссоциации слабого электролита связана с изменением энергии Гиббса в процессе диссоциации этого электролита соотношением:
ΔGT0 = — RTlnKд (5)
Уравнение (5) используется для расчета констант диссоциации слабых электролитов по термодинамическим данным.
Примеры решения задач
Задача 1. Определите концентрацию ионов калия и фосфат-ионов в 0,025 М растворе K3PO4.
Решение. K3PO4 – сильный электролит и в водном растворе диссоциирует полностью:
K3PO4 → 3К+ + РО43-
Следовательно, концентрации ионов К+ и РО43- равны соответственно 0,075М и 0,025М.
Задача 2. Определите степень диссоциации αд и концентрацию ионов ОН— (моль/л) в 0,03 М растворе NH3·H2О при 298 К, если при указанной температуре Кд(NH3·H2О) = 1,76× 10— 5.
Решение. Уравнение диссоциации электролита:
NH3·H2О → NH4+ + OH—
Концентрации ионов: [NH4+] = αС ; [OH—] = αС , где С – исходная концентрация NH3·H2О моль/л. Следовательно:
Kд = αС · αС /(1 — αС)
Поскольку α << 1, то:
Кд ≈ α 2С
Константа диссоциации зависит от температуры и от природы растворителя, но не зависит от концентрации растворов NH3·H2О. Закон разбавления Оствальда выражает зависимость α слабого электролита от концентрации.
α = √(Кд / С) = √(1,76× 10— 5 / 0,03) = 0,024 или 2,4 %
[OH—] = αС, откуда [OH— ] = 2,4·10— 2·0,03 = 7,2·10-4 моль/л.
Задача 3. Определите константу диссоциации уксусной кислоты, если степень диссоциации CH3CОOH в 0,002 М растворе равна 9,4 %.
Решение. Уравнение диссоциации кислоты:
CH3CОOH → СН3СОО— + Н+.
α = [Н+] / Сисх(CH3CОOH)
откуда [Н+] = 9,4·10—2·0,002 = 1,88·10-4 М.
Так как [CH3CОO—] = [Н+] и [CH3CОOH] ≈ Сисх(CH3CОOH), то:
Kд = [Н+]2 / Сисх(CH3CОOH)
Константу диссоциации можно также найти по формуле: Кд ≈ α 2С.
Задача 4. Константа диссоциации HNO2 при 298К равна 4,6× 10— 4. Найдите концентрацию азотистой кислоты, при которой степень диссоциации HNO2 равна 5 %.
Решение.
Кд =α 2С , откуда получаем Сисх(HNO2) = 4,6·10— 4/(5·10— 2)2 = 0,184 М.
Задача 5. На основе справочных данных рассчитайте константу диссоциации муравьиной кислоты при 298 К.
Решение. Уравнение диссоциации муравьиной кислоты
НСООН →Н+ + СООН—
В “Кратком справочнике физико–химических величин” под редакцией А.А. Равделя и А.М. Пономаревой приведены значения энергий Гиббса образований ионов в растворе, а также гипотетически недиссоциированных молекул. Значения энергий Гиббса для муравьиной кислоты и ионов Н+ и СООН— в водном растворе приведены ниже:
| Вещество, ион | НСООН | Н+ | СООН— |
| ΔGT0, кДж/моль | — 373,0 | 0 | — 351,5 |
Изменение энергии Гиббса процесса диссоциации равно:
ΔGT0 = — 351,5- (- 373,0) = 21,5 кДж/моль.
Для расчета константы диссоциации используем уравнение (5). Из этого уравнения получаем:
lnKд = — Δ GT0/RT= — 21500/(8,31 298) = — 8,68
Откуда находим: Kд = 1,7× 10— 4.
Задачи для самостоятельного решения
1. К сильным электролитам в разбавленных водных растворах относятся:
- СН3СOOH
- Na3PO4
- NaCN
- NH3
- C2H5OH
- HNO2
- HNO3
13.2. К слабым электролитам в водных растворах относятся:
- KAl(SO4)2
- NaNO3
- HCN
- NH4Cl
- C2H5OH
- H2SO3
- H2SO4
3. Определите концентрацию ионов NH4+ в 0,03 М растворе (NH4)2Fe(SO4)2;
4. Определите концентрацию ионов водорода в 6 мас.% растворе H2SO4, плотность которого составляет 1,038 г/мл. Принять степень диссоциации кислоты по первой и второй ступеням равной 100 %.
5. Определите концентрацию гидроксид-ионов в 0,15 М растворе Ba(OH)2.
6. Степень диссоциации муравьиной кислоты в 0,1 М растворе равна 4 %. Рассчитайте Концентрацию ионов водорода в этом растворе и константу диссоциации НСООН.
7. Степень диссоциации муравьиной кислоты в водном растворе увеличится при:
а) уменьшении концентрации HCOOH;
б) увеличении концентрации HCOOH;
в) добавлении в раствор муравьиной кислоты HCOONa;
г) добавлении в раствор муравьиной кислоты НCl.
8. Константа диссоциации хлорноватистой кислоты равна 5× 10— 8. Определите концентрацию HClO, при которой степень диссоциации HClO равна 0,5 %, и концентрацию ионов Н+ в этом растворе.
9. Вычислите объем воды, который необходимо добавить к 50 мл 0,02 М раствора NH3·H2О, чтобы степень диссоциации NH3·H2О увеличилась в 10 раз, если Кд(NH4OH) = 1,76·10— 5.
10. Определите степень диссоциации азотистой кислоты в 0,25 М растворе при 298 К, если при указанной температуре Кд(HNO2) = 4,6× 10— 4.
Зависимость между константой равновесия и степенью диссоциации имеет разную форму для разных реакций. Рассмотрим основные виды реакций, встречающихся в процессах горения. [c.215]
Зто уравнение дает зависимость между константой равновесия и степенью диссоциации. Так как константа равновесия для определенной температуры имеет вполне определенное значение, то степень диссоциации определяется давлением, при котором происходит диссоциация. Для выяснения этого влияния в правой части уравнения (19.12) числитель и знаменатель разделим на [c.216]
Изучение формул зависимостей между константой равновесия и степенью диссоциации приводит к заключению, что константа равновесия представляет гораздо более удобную расчетную величину, чем степень диссоциации, поэтому за основу расчета состава про- [c.216]
Константа равновесия и степень диссоциации [c.485]
Для того чтобы установить связь между константами равновесия и степенью диссоциации, выразим концентрации реагентов через степень диссоциации, воспользовавшись снова примером разложения четырехокиси азота. Из сказанного выше очевидно, что [c.487]
Полученное выражение и является искомой зависимостью Кр =>/( ). Аналогичным методом можно составить уравнение связи между константой равновесия и степенью диссоциации для реакций второй или третьей группы. [c.276]
Диссоциация. Изучение явления диссоциации, т. е. частичного или полного распада вещества на составные части, имеет большое практическое значение для сохранения полноты химической реакции и уменьшения тепловых потерь. Последнее, например, может быть при диссоциации отдельных газов продуктов горения. При рассмотрении влияния процесса диссоциации на равновесие пользуются понятием степени диссоциации, обозначаемой а. Под степенью диссоциации понимают долю моля конечного вещества, разложившегося к моменту химического равновесия. Ясно, что чем больше а, тем глубже протекает обратная реакция (диссоциация) и менее полной будет прямая реакция (ассоциация). Причем начальные вещества при химическом равновесии будут иметь большие концентрации и больше будет величина Ке, т.е. константа равновесия и степень диссоциации связаны между собой прямой зависимостью. Явный вид уравнения /Сс = / ( ) будет зависеть от типа реакций, определяемого знаком изменения числа молей Ап = 2 — т. е. будет ли Ап < О, А/г > О или Ап — 0. [c.196]
Пример. Чтобы проиллюстрировать использование константы равновесия, подсчитаем степень диссоциации трехокиси серы в двуокись серы и кислород в соответствии с химическим уравнением [c.263]
Задача решалась в два этапа. На первом этапе были вычислены термодинамические функции компонент воздуха и константы равновесия для реакций диссоциации, образования N0 и ионизации. На этом этапе задача фактически сводилась к вычислению соответствующих статических сумм для внутренних степеней свободы частиц. [c.277]
Одной из основных характеристик теории электролитической диссоциации является степень диссоциации а растворенного вещества, представляющая собой отношение числа молекул, распавшихся на ионы, к общему числу молекул, введенных в раствор, и изменяющаяся от О (отсутствие диссоциации) до 1 (полная диссоциация). Выражение для константы равновесия реакции электролитической диссоциации, называемой константой диссоциации в разбавленных растворах может быть записано в следующей форме [c.6]
Вывести формулу для расчета степени диссоциации газа Через константу равновесия для реакции диссоциации, происходящей по схеме Х2 2Х1 (диссоциация по такой схеме происходит, например, в парах щелочных металлов). При выводе формулы считать, что одноатомный и двухатомный газы являются идеальными. [c.170]
Между степенью диссоциации а и константой равновесия К существует прямая зависимость следовательно, с увеличением степени диссоциации константа равновесия увеличивается н наоборот. Имея значения констант равновесия, можно вычислить степень диссоциации при любой температуре и любом давлении. [c.302]
Определить степень диссоциации окиси углерода в газогенераторе при давлении в нем р =- 0,085 МПа и 7 === 2000 К, если константа равновесия при этих условиях Кр — 5,62-10 . [c.312]
Для ненасыщенного раствора (рис, 9.5, а) число степеней свободы будет С = 2+ 2 — 2 = 2 или р = f(T, х), где х — состав ненасыщенного раствора (обозначение р о введено для давления диссоциации, зависящего не только от температуры, но и концентрации раствора). Таким образом, Pq не может уже рассматриваться как константа равновесия, зависящая только от температуры, но эта величина будет определять энергию Гиббса, соответствующую данной системе [c.318]
Имея в виду, что константа равновесия Кр зависит только от температуры и при постоянной температуре остается неизменной, можно заключить, что степень диссоциации данной реакции увеличивается с увеличением объема и уменьшается с увеличением давления. [c.83]
Таким образом, для каждой конкретной реакции может быть получено выражение, связывающее константу равновесия с мерой реакции (степенью превращения, степенью диссоциации) и объемом или давлением. Эти выражения дают возможность оцепить влияние объема и давления на положение равновесия, а также определить меру реакции (степень превращения, степень диссоциации), если известны константа равновесия (или наоборот) и. следовательно, равновесный состав смеси. Знание равновесного состава смеси очень важно для практики. Так же важно установление влияния давления и объема на гке ложение равновесия. [c.199]
Если степень диссоциации Н О при заданной температуре равна а, то для каждого моля остается (1—а) молей Н О и образуется а молей Hj и молей О . В данной реакции константа равновесия зависит от объема системы, так как = [c.161]
В цилиндре ДВС продукты сгорания бензина в воздухе состоят из СО, СО2, Н2О, N2 и О2 температура в цилиндре равна 2200° К определить степень диссоциации СО2, парциальное давление которой равно 5 ат, а константа равновесия при 2200° К равна /Ср = 0,624 10- . [c.111]
После этого для частного случая — водяного пара и углекислого газа — выводится формула, устанавливающая зависимость степени диссоциации от значения константы равновесия Кс- [c.184]
Изменение температуры газа влияет на степень неравновесности течения как через скорости химических реакций, так и через изменение уровня диссоциации газа перед соплом. Константы скорости реакций рекомбинации слабо зависят от температуры, поэтому основное влияние на скорость процесса оказывают активные радикалы, концентрации которых с ростом температуры увеличиваются. С другой стороны, с ростом температуры увеличивается степень диссоциации газа перед соплом, и, следовательно, может возрасти доля энергии, теряемой из-за неравновесности процесса. Поэтому изменение температуры может приводить как к увеличению, так и к уменьшению степени отклонения системы от равновесия, в зависимости от того, какой фактор окажется преобладающим. [c.196]
Формулы (12.18) и (12.19) позволяют вычислить константу равновесия по найденной степени диссоциации или решить обратную задачу. [c.197]
При принятой форме записи реакций, когда прямая реакция является реакцией диссоциации, значение константы равновесия возрастает с увеличением температуры. Эта зависимость чрезвычайно резкая, степень диссоциации быстро возрастает с увеличением температуры и уменьшается при снижении ее. [c.70]
Sv = О — объем и давление не входят в вырантение для константы равновесия и, следовательно, не влияют на степень диссоциации. [c.199]
Согласно (16.4.2), повышение энтальпии и энтропии активного вещества изменяет константу равновесия реакции. Это следует учитывать, если активность твердой фазы высока. В качестве примера рассмотрим термическое разложение известняка СаСОз ii СаО+СОг- Каждой данной температуре соответствует вполне определенная степень диссоциации (равновесное давление СОг) Используя стандартные значения энтропии, можно подсчитать константу равновесия (равновесное давление) этой реакции. Фактически равновесное давление определяется активностью обоих твердых компонентов. Экспериментально получаются более высокие равновесные давления, если исходят из активного СаСОз, или меньшие давления, если в активном состоянии находится СаО. Величина константы диссоциации (или соответствующего давления СОг) зависит от степени активности (рис. 16.9). С повышением степени измельчения исходного известняка (СаСОз) увеличиваются давление и степень диссоциации. [c.456]
Впервые о существовании в парах щелочных металлов двухатомных молекул стало известно в 30-е годы [48, 49]. В настоящее время общепризнано, что пары щелочных металлов при давлениях, далеких от критических, являются частично димери-зованными, т. е. содержат не только атомы, но и многоатомные молекулы [50]. Состояние равновесия при заданных температуре и давлении характеризуется определенными концентрациями атомов и молекул. Эти концентрации определяются константой равновесия, соответствующей реакции диссоциации — рекомбинации. Доля каждой компоненты в паре определяется через параметр а, называемый степенью диссоциации. По определению, величина а является долей числа молекул, продиссоциировавших в данном равновесном состоянии пара с параметрами Р и Г. Таким образом, пары металлов следует рассматривать как химически реагирующую смесь атомарной и молекулярной компонент. В натриевых тепловых трубах по ходу парового потока возможно протекание реакции диссоциации — рекомбинации [c.65]
Фазы F — однородные газообразные, жидкие или твёрдые части системы. Компоненты К — составные части (простые элементы или соединения), образующие вещества, из которых состоит система. Степени свободы L — условия (температура, давление, концентрации), которые в известных пределах можно изменять, не нарушая состояния равновесия (числа фаз) системы. Для систем, находящихся в состоянии равновесия, согласно правилу фаз Гиббса, L = К — F, где К — наименьшее число молекул, которыми может быть выражен химический состав любой фазы данной системы. Например, для реакции диссоциации известняка СаО + СО2 = = a Og+Q, по правилу фаз, К=2 (СаО и СО.2), F = 3 (известняк, известь и газ) и тогда Z, = 2 + 2—3 = 1. Таким образом, если, используя единственную степень свободы, задаться температурой, то давление (упругость диссоциации) углекислого кальция будет иметь строго определённое значение. Это следует также из того, что константа равновесия данной реакции Кр = Pqq. [c.166]
Концентрацию недиссоциированной кремниевой кислоты без существенной ошибки можно принять равной ее общей концентрации, т. е. [НА] = 1,43- 10 . Однако при решении этой задачи нельзя уже игнорировать воду, константа диссоциации которой близка к первой константе кремниевой кислоты. В растворе этого соединения необходимо учитывать и присутствие ионов ОН от воды. Тогда по закону равенства зарядов (его также называют законом электронейтральности растворов) получим [Н ] = [ОН ] -Ь [А ]. Кроме того, [Н ] [ОН ] = 10 Решая относительно [Н ] эту систему уравнений, получаем, что в растворе кремниевой кислоты, находящемся в равновесии с нераство-рившимся веществом, концентрация ионов водорода должна соответствовать значению pH = 6,77, а степень диссоциации этой кислоты а = 0,8 10″ , т. е. 0,008%. [c.238]
Изучение термодинамических условий восстановления жидкой окиси хрома углеродом осложняется отсутствием термодинамических характеристик для жадких СггОз и карбидов хрома. Устойчивость карбидов СгуСз в расплаве Елютин и др. [88] рассчитывали следующим образом. Величину степени диссоциация карбида а вычисляли из уравнения константы равновесия реакции диссоциации [c.64]
По известному значению константы равновесия реакции из этого ураозиания может быть вычислена степень диссоциация водяного пара при данных услов(Иях. [c.299]
Для реакции 2Н2 + 02= =г=2Н20 (п) написать выражение константы равновесия Кр и Кс-, если известна степень диссоциации а. [c.111]
Зависимость парциального давления СО2 от температ)фы будет определяться константой равновесия (рис. 1.19). Для реакции 2СОг = = 2СО + О2 степень диссоциации подсчитывают, исходя из того, что из двух молекул СО2 получают две молекулы СО и одну молекулу О2. [c.36]
Вместе с тем ясно, что чем меньше концентра ия ОН в растворе, тем менее возможно образование гидроокиси и тем более вероятно получение чистого металла. Количество двухвалентных ионов зависит кроме степени кислотности растюра также и от количества уже вооотаншленных трехвалентных ионов, от степени диссоциации присутствоважшей или под влиянием тока возникшей гидроокиси. Константа равновесия последней [c.297]
Из уравнения (Х.9) следует, что концентрация СиО в металле уменьшается с увеличением содержания В2О3 и с уменьшением константы равновесия К, значение которой тем меньше, чем меньше степень диссоциации соединения в шлаке. [c.174]
Обратное влияние неравновесной колебательной релаксации на протекание химических реакций учитывается домножением констант диссоциации молекул О2 и N1 на некоторые функции Р(Т2, Т), Р(Т , Т), приведенные в [12-15]. Ввиду малости концентраций заряженных компонентов дальних следов за телами, входящими в плотные слои атмосферы со скоростями К , 8 км/с, пренебрегается неравновесностью возбуждения колебательных степеней свободы ионов. Считается, что возможно отсутствие термического равновесия между электронами и тяжелыми частицами, т.е. возможен отрыв температуры Т , от Т. При этом константы скоростей приведенных выше химических реакций с участием электронов предполагаются зависящими от температуры электронов [10, И]. Предполагается также, что след является квази-нейтральным, электрический ток отсутствует (диффузия заряженных компонентов имеет амбиполярный характер). [c.155]



