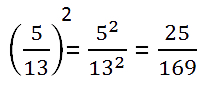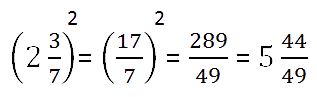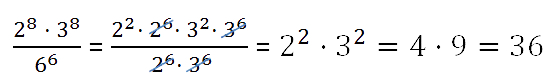Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя – как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с такого проверочного действия, как формулирование базовых определений.
Возвести число в степень – это вычисление значения степени некоторого числа.
То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0,5 в пятую степень”, это следует понимать как “вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Вычислите значение 3272
Как будем решать
Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи 
От основания степени это не зависит.
Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.
Выполните возведение 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
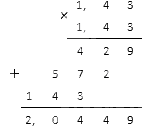
Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай – возведение числа в минус первую (минусовую) степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную – значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Возведение степени в степень
Как степень возвести в степень? Рассмотрим пример.
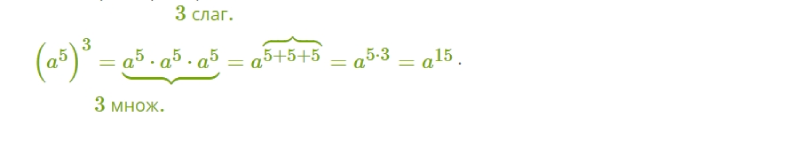
Здесь а – это любое число, а n и m – натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.
Все примеры воззведения в степень можно найти в интернете в удобных таблицах.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Возведение дроби в степень
Поддержать сайт
Запомните!
При возведении в степень дроби нужно
возвести в степень и числитель, и знаменатель.
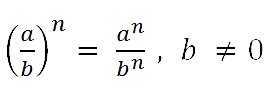
Данное свойство соответствует другой записи свойства № 5
«Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
-
()2 =
=
=
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой
части, превращая смешанное число в неправильную дробь. После этого
возводим в степень и числитель, и знаменатель.
Пример.
Формулу возведения в степень дроби применяют как
слева направо, так и справа налево, то есть, чтобы
разделить друг на друга степени
одинаковыми показателями, можно разделить одно основание на другое,
а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления и
возвести число в степень онлайн.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Дробная степень
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
Определение.
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
2) При a=0 и r>0
В частности,
При a<0 степень с дробным показателем не определяется.
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с рациональными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать таблицу степеней и следующее свойство корня:
Примеры.
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
А как вычисляется отрицательная дробная степень?
Степень с отрицательным рациональным показателем также определена только для a>0:
При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:
Примеры.
Выполнить возведение в степень с отрицательным рациональным показателем:
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Использование дробей в качестве степеней значительно упрощает жизнь по сравнению с записью выражений с помощью корней. Это связано с тем, что совершать арифметические действия с дробями легче, чем применять и помнить свойства корней. Поэтому ниже мы рассмотрим, как перейти от корней к числу в дробной степени.
Возведение в дробную степень проводится соответственно следующему правилу:
Пусть $frac{p}{q}$ — обыкновенная дробь, причём $p$ и $q$ больше нуля и $q≠1$. Тогда для возведения числа $a$ в дробную степень необходимо извлечь из него корень $q$-ой степени и возвести в степень числителя, равную $p$.
В математической форме это тождество записывается так:
$a^{frac{p}{q}}=sqrt[q]{a^p}, a≥0, p>0, q>1$.
Замечание 1
Следует отметить, что в случае использования в качестве записи дробной степени вместо корней есть одно важное правило. Запрещается возводить в дробную степень отрицательные числа.
Это связано с тем, что в таком случае можно прийти к невыполнимому равенству, например:
$-3=(-27)^{frac{1}{3}}=(-27)^{frac{2}{6}}=sqrt[6]{(-27)^2}=sqrt[6]{729}=3$.
Правило для возведения степени в степень в случае, когда показатель степени является дробным числом, выполняется также как и для обычной целой степени, то есть:
Число $a$ в дробной степени вида $frac{p}{q}$, возведённое в степень $b$, равно числу $a$, возведённому в степень произведения дроби и числа $b$.
В математической форме это выглядит так:
$(a^{frac{p}{q}})^b= a^{frac{p cdot b}{q}}$.
Замечание 2
Правило для возведения числа в дробную степень справедливо не только для обыкновенных дробей, но и для десятичных и неправильных.
В случае, если необходимо возвести число в десятичную или неправильную дробь, сначала необходимо перевести её в обычную чтобы стали видны показатели степени числа и корня.
Возведение в нецелую отрицательную степень проводится по тем же правилам, что и возведение в целую отрицательную степень, то есть:
Пусть $frac{p}{q}$ — обыкновенная дробь и $q≠1$, а $a>0$, тогда $a^{-frac{p}{q}}$ равно $frac{1}{a^{frac{p}{q}}}$.
Запишем в математической форме:
$a^{-frac{p}{q}}=frac{1}{a^{frac{p}{q}}}, a>0, p>0, q>1$.
Пример 1
Вычислите арифметические корни из следующих выражений:
- $64^{frac{1}{6}};$
- $81^{frac{3}{4}};$
- $0^{frac{51}{4}}$.
Решение:
-
$64^{frac{1}{6}}=sqrt[6]{64}=2$;
-
$81^{frac{3}{4}} = sqrt[4]{81^3}=27;$
-
$0^{frac{51}{4}}=sqrt[4]{0^51}=0.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Из статьи вы узнаете, как возвести число в дробную степень, что для этого нужно понимать и уметь. Приведены поучительные примеры с дробными степенями.
Как возводить в дробную степень
Как возвести число в натуральную степень, легко усваивают почти все учащиеся. Достаточно помножить его само на себя столько раз, сколько указано в показателе степени. Например, запись 23 означает, что число 2 нужно умножить само на себя три раза, а запись (1,4)5 значит (1,4)5=1,4*1,4*1,4*1,4*1,4.
А вот запись типа 35/6 для многих совершенно не понятна. Возникает конфликт восприятия ранее усвоенного понимания возведения числа в степень со здравым смыслом, ведь написать число помноженным само на себя 5/6 раз, просто невозможно.
Подобный вопрос возникает у тех, кто не усвоил тему извлечения из чисел корня.
Напомним, что извлечение корня из числа, это математическая операция обратная операции возведения его в степень. Она подразумевает разложение его на одинаковые множители, число которых равно показателю корня. В частности, 3√8 равно 2, ведь, как видно из приведённого ранее примера 23 = 2*2*2 = 8.
Некоторые, при изучении извлечения корня из числа упускают один факт. Корень записывается не только в виде q√a (где a некоторое число, а q – показатель корня) он может быть записан и в виде a1/q. Надеюсь, теперь смысл дробной степени вам становится ясен. q в знаменателе дроби, это и есть корень. В числителе стоит та степень, в которую указанное число нужно возвести. В данном случае она равна одному (p=1). Если бы она была равна двум (p=2), то следовало бы записать a1/q *a1/q. Эта запись равносильна a2/q. Если бы она равнялась трём (p=3), т. е. 3/q √a, то вышло бы a1/q*a1/q*a1/q.
Теперь обобщим всё выше сказанное.
ap/q = q√ap. При этом a ≥ 0, p>0 и q>1.
Если в дробную степень требуется возвести неправильную либо десятичную дробь, сначала они приводятся к виду обычной дроби, чтобы ясно стали видны числитель и знаменатель, т. е. показатели корня и степени.
О свойствах дробных степеней
Приведём самые главные свойства дробных степеней, которые чаще всего приходится использовать в вычислениях.
- [a^{p}* a^{q}=a^{p+q}]
- [a^{p} / a^{q}=a^{p-q}]
- [left(a^{p}right)^{q}=a^{p^{*} q}]
- [left(a^{*} bright)^{p}=a^{p} b^{p}]
- [(a / b)^{p}=a^{p} / b^{p}]
Из свойства 3 следует, что [left(a^{p / q}right)^{b}=a^{left(p^{*} bright) / q}]
Нет времени решать самому?
Наши эксперты помогут!
Примеры возведения в дробную степень
[81^{1 / 4}=sqrt[4]{81}=3]
[135^{9 / 10}={ }^{10} sqrt{135^{9}}]. Извлекать корень и возводить в степень не имеет смысла т. к. число
получится очень сложным, а указанная запись наиболее простая.
[left.[1(3 / 5)]^{1 / 3}=(8 / 5)^{1 / 3}={ }^{3} sqrt{(8 / 5)^{1}}={ }^{3} sqrt{(} 2^{3} / 5right)=2 /
sqrt{5} 3]. Здесь, для упрощения выражения, мы выполнили действие вынесения из-под знака корня числа 2.
Зачем нужны числа в дробной степени
Решение дробных степеней проще, чем вычисление корней. Оно занимает меньше шагов и, при наличии определённого навыка и меньше усилий. Так считают все, кто занимается математикой.