Время на прочтение
3 мин
Количество просмотров 114K
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
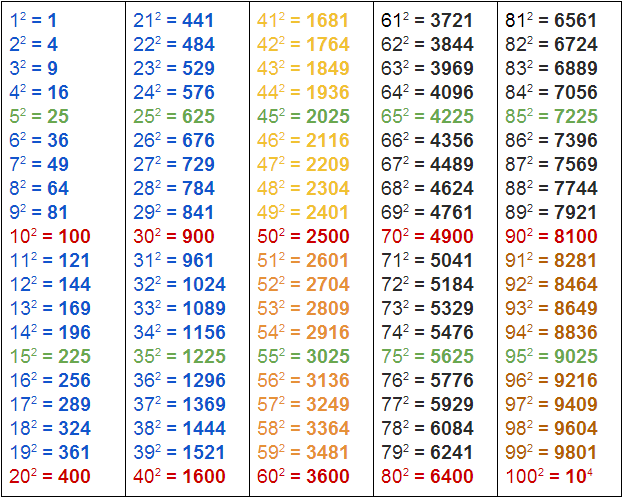
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
75 * 75 = 7 * 8 = 56 … 25 = 5625.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
XX * XX = 1500 + 100 * вторую цифру + (10 - вторая цифра)^2
Достаточно трудно, верно? Давайте разберем пример:
43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849.
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
XX * XX = 2500 + 100 * вторую цифру + (вторая цифра)^2
Тоже достаточно трудно для восприятия. Давайте разберем пример:
53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809.
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
XX * XX = 8000+ 200 * вторую цифру + (10 - вторая цифра)^2
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649.
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
XX * XX = 100(XX - 25) + (50 - XX)^2
Например:
37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369
Для чисел от 50 до 100
XX * XX = 200(XX - 50) + (100 - XX)^2
Например:
67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
(a+b)^2 = a^2 + 2ab + b^2.
56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136.
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:
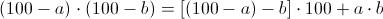
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
92*92 = (92-8)*100+8*8 = 8464
(от sielover)
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Возведение в степень: определение
Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.
Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:
43, где 4 — это основание, а 3 — показатель. Также 43 = 4·4·4 = 64
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Основные правила выполнения данных вычислений:
- итог возведения отрицательного основания в четную степень — положительный;
- итог возведения отрицательного основания в нечетную — отрицательный;
- итог возведения положительного основания в любую — положительный;
- любое основание с показателем один равно себе;
- ноль при любом возведении в результате дает ноль;
- единица с любым показателем равна единице;
- любое основание с показателем ноль равно единице.
Таблица представляет собой ряд чисел, возведенных в определенные степени.
Свойства степеней
a, b — любое рациональное число, n, m — любое натуральное
Произведение степеней
Данное действие подразумевает то, что одинаковое основание остается без изменений, а показатели складываются.
(a^ncdot a^m=a^{n+m})
Частное степеней
Под выполнением данной операции понимается то, что одинаковое основание остается без изменений, а из показателя делимого вычитают показатель делителя.
(frac{a^m}{a^n}=a^{m-n})
Возведение степени в степень
Для вычисления результата этой операции основание остается без изменения, а показатели перемножаются.
(left(a^mright)^n=a^{mcdot n})
Степень произведения
Для выполнения этого арифметического действия каждый из множителей возводится в степень, после чего полученные результаты перемножаются.
(left(acdot bright)^n=a^ncdot b^n)
Степень частного
Чтобы выполнить данную арифметическую операцию, следует возвести в степень делимое и делитель, а затем первый результат разделить на второй.
(left(frac{a}{b}right)^n=frac{a^n}{b^n})
Виды таблиц
Таблица степеней натуральных чисел
Натуральными являются те числа, которые получаются при счете предметов. Наименьшее — один, наибольшего не существует.
Чтобы вычислить результат возведения, нужно основание умножить само на себя столько раз, сколько указано в показателе. То есть основание а с показателем n значит, что а нужно умножить на себя n раз.
аn = а·а·…·а
Таблица для чисел от одного до десяти:
Таблица отрицательных степеней
Деление является обратной операцией умножению. Отрицательный показатель указывает на то, сколько раз необходимо разделить число. Легче всего представить в виде десятичной дроби:
(а^{-n} = frac{1}{а*а*dots*а})
Для вычисления (а^{-n}) нужно:
- Возвести а в степень n.
- Затем разделить единицу на полученный результат, то есть (frac{1}{a^n}).
Пример таблицы для двойки:
Таблица степеней двузначных чисел
Двузначное число – это комбинация двух однозначных цифр.
Таблица квадратов от 1 до 100:
Степени от 1 до 10: пример
Квадраты чисел до 100: пример
Математические хитрости при возведении в квадрат двузначных чисел
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Алякшин Е.Ю. 1
1МБОУ “ООШ № 4”
Урженко Г.Д. 1
1МБОУ “ООШ № 4”
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Я учусь в 7 классе. По математике у меня оценка «4». Недавно мы проходили тему «Натуральный показатель степени» по этой теме у меня вышло удовлетворительно. Я задумался: Почему? Я знаю все формулы, умею их применять, но за контрольные и самостоятельные работы не получаю оценку выше «4». Наверно, потому, что мне не хватает времени доделать ее до конца. Проанализировав эту ситуацию, я понял, что много времени трачу на вычисления. Тогда я начал искать в интернете ответ на вопрос: Как научиться быстро возводить в степень двузначные числа? И наткнулся на книгу Ингве Фогта «Математические трюки для быстрого счета».
Умение выполнять расчеты необходимо каждому человеку. Без умения считать невозможно, жить в современном мире. Конечно, есть калькулятор, но он не всегда под рукой.
Устный счет – математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты и т.п.). [Википедия]
Цель : Изучить и научиться применять некоторые способы быстрого возведения в степень двузначных чисел, для производства которых, достаточно устного счета или применения ручки и бумаги.
Объект исследования: возведение в степень чисел начинающихся и заканчивающихся на 5; возведение в квадрат числа методом «Обратной пирамиды»
Для достижения данной цели необходимо решить следующие задачи:
используя литературу;
рассмотреть основной прием возведения двузначных чисел в квадрат;
научиться возведению в степень числа начинающихся и заканчивающихся на 5; возведение в квадрат числа методом «Обратной пирамиды»;
изучить метод возведения в квадрат трехзначного числа
Методы исследования: изучение теории по выбранной теме, анализ литературы, практическое применение знаний, умений и навыков.
Этапы проекта: выбор темы исследования; определение цели, задач, методов исследования; изучение литературы; сбор материала; анализ и обобщение полученной информации; текстовое оформление исследования; практическая работа; формулировка выводов; представление результатов исследовательской работы.
Актуальность выбранной темы.
Мой интерес к теме возник на уроках математики, при изучении темы «Степень с натуральным показателем». При этом я заметил, что не только у меня, но и у моих одноклассников возникали трудности при возведении двузначных чисел в степень. Современная жизнь делает эти задачи актуальными, так как сфера практического применения быстрого счета безгранична. Без умения считать современном обществе просто трудно было бы существовать.
Гипотеза. Научиться быстро считать легко.
Все умеют считать, но считать быстро умеют единицы
Обзор литературы
1.1 История возникновения степени числа
Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.
В своей знаменитой «Арифметике» Диофант Александрийский описывает первые натуральные степени чисел так:
«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».
Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михеля Штифеля «Полная арифметика» (1544 г.) сыграла в этом значительную роль.
«Сумма знаний…» Луки Пачоли была одним из первых опубликованных сочинений. Но математики продолжали искать более простую систему обозначений так как его обозначения были не удобны.
Француз, бакалавр медицины Никола Шюке смело ввёл в свою символику не только нулевой, но и отрицательный показатель степени. Он писал его мелким шрифтом сверху и справа от коэффициента.
В XVI в. итальянец Раффаэле Бомбелли в своей «Алгебре» использовал ту же идею. Он обозначал неизвестное специальным символом 1, а символами 2, 3, – его степени. Обозначения Бомбелли также оказали влияние и на символику нидерландского математика Симона Стевина (1548—1620). Он обозначал неизвестную величину кружком О, внутри которого указывал показатели степени. Стевин предложил называть степени по их показателям – четвёртой, пятой и т. Д. и отверг Диофантовы составные выражения «квадрато-квадрат», «квадрато-куб».
У Рене Декарта в его «Геометрии» (1637) мы находим современное обозначение степеней а2, а3,… Любопытно, что Декарт считал, что а*а не занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей. Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а2.[3, Википедия]
2.Собственные исследования
Одни из многих методов научиться возведению в степень чисел начинающихся и заканчивающихся на 5; возведение в квадрат числа методом «Обратной пирамиды» всего за несколько секунд, проверять верность полученного ответа и, что немаловажно, находить столбец, в котором прячется ошибка, если таковая имеется.
Я решил научиться этим методам.
2.1 Возведение в квадрат двузначных чисел заканчивающиеся на 5:
Чтобы возвести в квадрат: число десятков умножаем на следующие число стоящее, а натуральном ряду и приписываем 25[1,36]
Пример 1
2 52=625
(2*3)=625
Пример 2
7 52=5625
(7*5)=5625
2.2 Возведение в квадрат двузначных чисел начинающегося на 5
Для возведения в квадрат двузначного числа, начинающегося на 5 нужно прибавить к 25 вторую цифру числа и приписать квадрат второй цифры, причём если квадрат второй цифры однозначное число ,то перед ним надо приписать цифру 0.[1,35]
Пример 3
|
562=3136 (25+6)=31 62=36 |
512=2601 (25+1)=26 12=1 |
2.3 Метод «Обратной пирамиды»
В первой строке в ряд записываются квадраты цифр возводимого в квадрат числа по порядку. Следующая строка представляет собой удвоенное произведение цифр числа. Умножение на 2 фигурирует во всех последующих примерах. Затем вся эта “пирамида наоборот” складывается в столбик и получается искомый результат.[2,c12]
Пример 1
|
6 |
4 |
4 |
9 |
|
1 |
1 |
2 |
|
|
7 |
5 |
6 |
9 |
8 7*87=7569
8 *8=64 7*7=49
8*7*2=112
|
4 |
9 |
3 |
6 |
|
8 |
4 |
||
|
5 |
7 |
7 |
6 |
Пример 2
7 6*76=5776
7 *7=49 6*6=36
2.4 Возведение трёхзначных чисел в квадрат
Для того чтобы возвести в квадрат трёхзначное число необходимо:
1.Последовательно возвести каждую цифру в квадрат (если получается однозначное число добавляем 0
2.Перемножаем первую и вторую цифру и на число 2 и вторую на третью и на число 2
3. Перемножаю первую и третью и на 2
4. Складываем полученный результат
7562=571536
1.7*5*2=70
2. 2*5*6=60
3 .6*7*2=84
-
7
5
6
4
9
2
5
3
6
7
0
6
0
8
4
5
7
1
5
3
6
2.5 Результаты и обсуждение
У многих моих одноклассников, также проблемы с быстротой вычислений. Я решил научить их быстрому возведению в квадрат двузначных чисел. Я пригласил своих друзей и дал им решить карточки с примерами на возведение чисел в степень. Самым быстрым из 6 человек оказался Ваня С, который посчитал за 3 минуты 20 секунд. Никто из ребят не решил пример правильно. Дольше всех считал Алексей С. – 9 минут.
752 452
462 952
642 5442
872 6092
Результаты вычисления представлены в таблице
|
Ваня С. |
3мин 20сек |
|
Алексей С. |
9 мин |
|
Владимир Ч. |
5мин 10 сек |
|
Юля Я. |
7мин 30 сек |
|
Даша М. |
5 мин |
|
Виика М. |
6 мин 10 сек |
После этого я показал ребятам все методы возведения в квадрат.. Две недели мы отрабатывали этот прием, и снова проверили быстроту счета, но уже по швейцарскому методу.
Результаты вычисления после изучения швейцарского метода представлены в таблице
|
Ваня С. |
1мин 50сек |
|
Алексей С. |
6мин 30 сек |
|
Владимир Ч. |
2 мин 10сек |
|
Юля Я. |
3 мин 30 сек |
|
Даша М. |
2 мин 10сек |
|
Виика М. |
3мин 20 сек |
Вывод
Владение приёмами быстрого возведения двузначного числа в квадрат даёт возможность выбрать в каждом отдельном случае наиболее рациональные и эффективные пути вычислений, что приводит:
к сокращению времени на вычисления;
к защите от массы вычислительных ошибок;
к ведению записи в строчку и отказа от традиционного письменного умножения.
Считаю, что возводить двузначные числа в квадрат легко и просто. Гипотеза доказана.
Умение считать в уме остаётся полезным навыком для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.
Возможность обходиться без калькулятора и в нужный момент оперативно решить поставленную арифметическую задачу – это здоров
Литература
Ингеве Фогт, Математические трюки для быстрого счета // ООО «Альпина Паблишер», 2020 – С. 170
Билл Хэндли, Считать в уме, как компьютер // Попурри, Минск, 2006 – С. 351
https://ru.wikipedia.org/wiki/Заглавная_страница
Просмотров работы: 151
Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя – как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с такого проверочного действия, как формулирование базовых определений.
Возвести число в степень – это вычисление значения степени некоторого числа.
То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0,5 в пятую степень”, это следует понимать как “вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Вычислите значение 3272
Как будем решать
Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи  .
.
От основания степени это не зависит.
Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.
Выполните возведение 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: 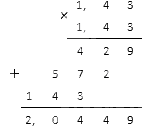
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай – возведение числа в минус первую (минусовую) степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную – значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Возведение степени в степень
Как степень возвести в степень? Рассмотрим пример.
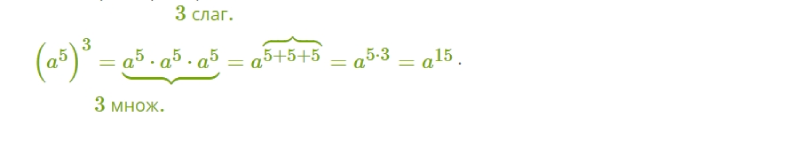 Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ.
Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ.
Здесь а – это любое число, а n и m – натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.
Все примеры воззведения в степень можно найти в интернете в удобных таблицах.
Степень числа, говоря простым языком – это то, сколько раз число последовательно умножили само на себя. Например, если мы хотим вычислить, чему будет равно число 2, возведенное в степень 4, то нам нужно число 2 перемножить само на себя 4 раза (2х2х2х2). В результате мы получи 16.
Число 2 здесь будет называться основание степени, а число 4, стоящее над двойкой – показателем. Правильно читается, как «два в степени четыре».
В степень можно возводить и положительные и отрицательные числа, с одной лишь разницей – положительное число, после возведения в степень, всегда останется положительным. Результат возведения в степень отрицательного числа, в свою очередь, будет зависеть от того, четной или нечетной была степень. Так (-2) в четвертой степени будет равняться 16, а (-2) в пятой степени будет равно (-32).
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Каждый раз высчитывать, чему равно число в некой степени, перемножая его вручную, крайне муторно. Куда проще воспользоваться таблицей степеней.
Это таблица степеней, показывающая результат возведения чисел от 1 до 10 в степени от 1 до 10. Пользоваться ей очень удобно. Нужно найти пересечение нужного числа и степени, и в этой точке будет написан результат возведения.
Ускоренное возведение в степень
Но что делать, если под рукой нет таблицы, и воспользоваться калькулятором тоже нет возможности? Существует достаточно простой алгоритм, который упростит вычисления. Предположим, что нам надо узнать, сколько будет 3 в степени 15. Для этого мы:
- Показатель степени раскладываем на сумму степеней с основанием 2. 15 – это 1+2^1+2^2+2^3, то есть 1+2+4+8.
- Затем последовательно возводим основание 3 в степени, получившиеся при разложении показателя степени. Это (3^1)x(3^2)x(3^4)x(3^8).
- Наконец, считаем результат. 3^1=3, 3^2=9, с этим все просто. Зная что, 3 в степени 2 равняется 9, легко вычислить, чему будет равно 3 в степени 4. Это (3^2)x(3^2), то есть 9х9, получается 81. Так же поступаем и с вычислением 3^8. Зная, что 3^4=81, для вычисления 3^8 перемножаем 81 и 81, получаем 6561. Теперь нужно вычислить результат 3х9х81х6561. Получаем 14 348 907.
Так или иначе, все равно придется производить сложные вычисления, но так вы сократите количество производимых умножений. В данном случае 6 операций умножения, взамен 15-кратного перемножения тройки саму на себя.
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
