Как найти степень любого числа - Сайт, где вы сможете решить свои вопросы

Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя – как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с такого проверочного действия, как формулирование базовых определений.

Определение 1

Возвести число в степень – это вычисление значения степени некоторого числа.

То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0,5 в пятую степень”, это следует понимать как “вычислите значение степени (0,5)5.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Пример 1

Условие: возведите -2 в степень 4.

Решение

Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.

Возьмем пример посложнее.

Пример 2

Вычислите значение 3272

Как будем решать

Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 327·327=237·237=52949=103949

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Пример 3

Выполните возведение в квадрат числа π.

Решение

Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.

Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

a1=a

Это понятно из записи .

От основания степени это не зависит.

Пример 4

Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.

Пример 5

Примеры:

50=1, (-2,56)0=1230=1

00- не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.

Пример 6

Выполните возведение 2 в степень -3.

Решение

Используя определение выше, запишем: 2-3=123

Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.

Тогда ответ таков: 2-3=123=18

Пример 7

Возведите 1,43 в степень -2.

Решение

Переформулируем: 1,43-2=1(1,43)2

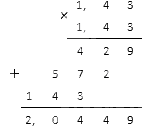
Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1,43)-2=1000020449

Отдельный случай – возведение числа в минус первую (минусовую) степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.

Пример 8

Пример: 3−1=1/3

913-1=13964-1=164 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.

Определение 2

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.

У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.

Проиллюстрируем на примере.

Пример 9

Вычислите 8-23.

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23

Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14

Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2

После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.

Пример 10

Возведите 44,89 в степень 2,5.

Решение

Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.

А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107

Ответ: 13 501,25107.

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную – значения не имеет: 0-43.

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Пример 11

Вычислите приближенное значение 2 в степени 1,174367….

Решение

Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.

Возведение степени в степень

Как степень возвести в степень? Рассмотрим пример.

Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ.

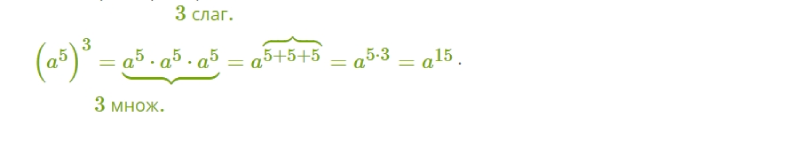
Здесь а – это любое число, а n и m – натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.

Все примеры воззведения в степень можно найти в интернете в удобных таблицах.

Источник

Возведе́ние в сте́пень — арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя. Степень с основанием и натуральным показателем обозначается как

${displaystyle a^{b}=underbrace {acdot acdot ldots cdot a} _{b},}$

где — количество множителей (умножаемых чисел)^[1]^{[К 1]}.

Например, ${displaystyle 3^{2}=3cdot 3=9;quad 2^{4}=2cdot 2cdot 2cdot 2=16}$

В языках программирования, где написание $a^{b}$ невозможно, применяются альтернативные обозначения^[⇨].

Возведение в степень может быть определено также для отрицательных^[⇨], рациональных^[⇨], вещественных^[⇨] и комплексных^[⇨] степеней^[1].

Извлечение корня — одна из операций, обратных возведению в степень, она по известным значениям степени ${displaystyle c=a^{b}}$ и показателя находит неизвестное основание . Вторая обратная операция — логарифмирование, она по известным значениям степени ${displaystyle c=a^{b}}$ и основания находит неизвестный показатель ${displaystyle b=log _{a}c}$ . Задача нахождения числа по известному его логарифму (потенцирование, антилогарифм) решается с помощью операции возведения в степень.

Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.

Употребление в устной речи[править | править код]

Запись ${displaystyle a^{n}}$ обычно читается как «a в -й степени» или «a в степени n». Например, $10^{4}$ читается как «десять в четвёртой степени», ${displaystyle 10^{3/2}}$ читается как «десять в степени три вторых (или: полтора)».

Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, $10^{2}$ читается как «десять в квадрате», $10^{3}$ читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо a^2 , ${displaystyle a^{3}}$ древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали^[2].

Число, являющееся результатом возведения натурального числа в -ую степень, называется точной -ой степенью. В частности, число, являющееся результатом возведения натурального числа в квадрат (куб), называется точным квадратом (кубом). Точный квадрат также называется полным квадратом.

Свойства[править | править код]

Основные свойства[править | править код]

Все приведенные ниже основные свойства возведения в степень выполняются для натуральных, целых, рациональных и вещественных чисел^[3]. Для комплексных чисел, в силу многозначности комплексной операции, они выполняются только в случае натурального показателя степени^[⇨].

${displaystyle a^{1}=a}$
$left(abright)^{n}=a^{n}b^{n}$
$left({a over b}right)^{n}={{a^{n}} over {b^{n}}}$
${displaystyle a^{n}a^{m}=a^{n+m}}$
$left.{a^{n} over {a^{m}}}right.=a^{n-m}$
$left(a^{n}right)^{m}=a^{nm}$ .

Запись $a^{n^{m}}$ не обладает свойством ассоциативности (сочетательности), то есть, в общем случае, $(a^{n})^{m}neq a^{left({n^{m}}right)}$ Например, ${displaystyle (2^{2})^{3}=4^{3}=64}$ , а $2^{left({2^{3}}right)}=2^{8}=256$ . В математике принято считать запись $a^{n^{m}}$ равнозначной $a^{left({n^{m}}right)}$ , а вместо $(a^{n})^{m}$ можно писать просто $a^{nm}$ , пользуясь предыдущим свойством. Впрочем, некоторые языки программирования не придерживаются этого соглашения.

Возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, $a^{b}neq b^{a}$ , например, $2^{5}=32$ , но ${displaystyle 5^{2}=25.}$

Таблица натуральных степеней небольших чисел[править | править код]

n	n²	n³	n⁴	n⁵	n⁶	n⁷	n⁸	n⁹	n¹⁰
2	4	8	16	32	64	128	256	512	1024
3	9	27	81	243	729	2187	6561	19 683	59 049
4	16	64	256	1024	4096	16 384	65 536	262 144	1 048 576
5	25	125	625	3125	15 625	78 125	390 625	1 953 125	9 765 625
6	36	216	1296	7776	46 656	279 936	1 679 616	10 077 696	60 466 176
7	49	343	2401	16 807	117 649	823 543	5 764 801	40 353 607	282 475 249
8	64	512	4096	32 768	262 144	2 097 152	16 777 216	134 217 728	1 073 741 824
9	81	729	6561	59 049	531 441	4 782 969	43 046 721	387 420 489	3 486 784 401
10	100	1000	10 000	100 000	1 000 000	10 000 000	100 000 000	1 000 000 000	10 000 000 000

Расширения[править | править код]

Целая степень[править | править код]

Операция обобщается на произвольные целые числа, включая отрицательные и ноль^[4]::

${displaystyle a^{z}={begin{cases}a^{z},&z>0\1,&z=0,aneq ;0\{dfrac {1}{a^{|z|}}},&z<0,aneq ;0end{cases}}}$

Результат не определён при a=0 и .

Рациональная степень[править | править код]

Возведение в рациональную степень где — целое число, а — натуральное, положительного числа определяется следующим образом^[4]:

${displaystyle a^{m over n}=({sqrt[{n}]{a}})^{m};quad forall a>0,ain mathbb {R} ,min mathbb {Z} ,nin mathbb {N} .}$

Степень с основанием, равным нулю, определяют только для положительного рационального показателя.

${displaystyle 0^{m over n}=0;quad min mathbb {N} ,nin mathbb {N} .}$

Для отрицательных степень с дробным показателем не рассматривается.

Следствие: ${displaystyle {sqrt[{n}]{a}}=a^{1/n};quad a>0,ain mathbb {R} .}$ Таким образом, понятие рациональной степени объединяет возведение в целочисленную степень и извлечение корня в единую операцию.

Вещественная степень[править | править код]

Множество вещественных чисел — непрерывное упорядоченное поле, обозначается . Множество вещественных чисел не является счётным, его мощность называется мощностью континуума. Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение^[5] соответствующих операций над рациональными числами.

Если даны два вещественных числа, представимые бесконечными десятичными дробями (где alpha – положительное):

${displaystyle alpha =a_{0},a_{1}a_{2}ldots a_{n}ldots ={a_{n}},~~alpha >0,}$

${displaystyle beta =pm b_{0},b_{1}b_{2}ldots b_{n}ldots ={b_{n}},}$

определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: $alpha =[a_{n}]$ и $beta =[b_{n}]$ , то их степенью называют число ${displaystyle gamma =[c_{n}]}$ , определённое степенью последовательностей ${a_{n}}$ и ${b_{n}}$ :

${displaystyle gamma =alpha ^{beta }{=}[a_{n}]^{[b_{n}]}=[a_{n}{widehat {}}b_{n}]}$

вещественное число ${displaystyle gamma =alpha ^{beta }}$ , удовлетворяет следующему условию:

${displaystyle (a'leqslant alpha leqslant a'')land (b'leqslant beta leqslant b'')Rightarrow ({(a')}^{b'}leqslant alpha ^{beta }leqslant {(a'')}^{b''})Rightarrow ({(a')}^{b'}leqslant gamma leqslant {(a'')}^{b''}),~~~forall ~a',a'',b',b''in mathbb {Q} ,~forall alpha >0,~alpha ,beta ,gamma in mathbb {R} .}$

Таким образом степенью вещественного числа ${displaystyle alpha ^{beta }}$ является такое вещественное число gamma которое содержится между всеми степенями вида ${displaystyle {(a')}^{b'}}$ с одной стороны и всеми степенями вида ${displaystyle {(a'')}^{b''}}$ с другой стороны.

Степень с основанием, равным нулю, определяют только для положительного вещественного показателя.

${displaystyle 0^{beta }=0;quad beta in mathbb {R} ,beta >0.}$

Для отрицательных alpha степень с вещественным показателем не рассматривается.

На практике для того, чтобы возвести число alpha в степень beta , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение степени ${displaystyle alpha ^{beta }}$ берут степень указанных рациональных чисел ${displaystyle a^{b}}$ . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают alpha и beta .

Пример возведения в степень ${displaystyle gamma =pi ^{e}}$ , с точностью до 3-го знака после запятой:

Полезные формулы:

${displaystyle x^{y}=a^{ylog _{a}x}}$

$x^{y}=e^{yln x}$

$x^{y}=10^{ylg x}$

Последние две формулы используют для возведения положительных чисел в произвольную степень на электронных калькуляторах (включая компьютерные программы), не имеющих встроенной функции $x^{y}$ , и для приближённого возведения в нецелую степень или для целочисленного возведения в степень, когда числа слишком велики для того, чтобы записать результат полностью.

Комплексная степень[править | править код]

Возведение комплексного числа в натуральную степень выполняется обычным умножением в тригонометрической форме. Результат однозначен:

${displaystyle z^{n}=r^{n}(cos varphi +isin varphi )^{n}=r^{n}(cos nvarphi +isin nvarphi );quad forall nin mathbb {N} ,zin mathbb {C} ,rin mathbb {R} }$

, (формула Муавра)^[6].

Для нахождения степени произвольного комплексного числа в алгебраической форме a + bi можно воспользоваться формулой бинома Ньютона (справедливой и для комплексных чисел):

${displaystyle (a+bi)^{n}=a^{n}+C_{n}^{1}a^{n-1}bi+C_{2}^{n}a^{n-2}b^{2}i^{2}+...+C_{n}^{n-1}ab^{n-1}i^{n-1}+b^{n}i^{n},quad forall nin mathbb {N} }$

Заменяя степени ${displaystyle i^{k}}$ в правой части формулы их значениями в соответствии с равенствами: ${displaystyle i^{4k}=1,i^{4k+1}=i,i^{4k+2}=-1,i^{4k+3}=-i,kin mathbb {N} }$ , получим:

${displaystyle (a+bi)^{n}=sum _{k=0}^{[n/2]}(-1)^{k}C_{n}^{2k}a^{n-2k}b^{2k}+isum _{k=0}^{[(n-1)/2]}(-1)^{k}C_{n}^{2k+1}a^{n-2k-1}b^{2k+1}.}$

^[7]

Основой для более общего определения комплексной степени служит экспонента $e^{z}$ , где — число Эйлера, z=x+iy — произвольное комплексное число^[8].

Определим комплексную экспоненту с помощью такого же ряда, как и вещественную:

${displaystyle e^{z}=1+z+{frac {z^{2}}{2!}}+{frac {z^{3}}{3!}}+{frac {z^{4}}{4!}}+cdots .}$

Этот ряд абсолютно сходится для любого комплексного поэтому его члены можно как угодно перегруппировывать. В частности, отделим от него часть для ${displaystyle e^{iy}}$ :

${displaystyle e^{iy}=1+iy+{frac {(iy)^{2}}{2!}}+{frac {(iy)^{3}}{3!}}+{frac {(iy)^{4}}{4!}}+cdots =left(1-{frac {y^{2}}{2!}}+{frac {y^{4}}{4!}}-{frac {y^{6}}{6!}}+cdots right)+ileft(y-{frac {y^{3}}{3!}}+{frac {y^{5}}{5!}}-cdots right).}$

В скобках получились известные из вещественного анализа ряды для косинуса и синуса, и мы получили формулу Эйлера:

${displaystyle e^{z}=e^{x}e^{yi}=e^{x}(cos y+isin y)}$

Общий случай $a^{b}$ , где a,b — комплексные числа, определяется через представление в показательной форме: ${displaystyle a=re^{i(theta +2pi k)}}$ согласно определяющей формуле^[8]:

${displaystyle a^{b}=(e^{operatorname {Ln} (a)})^{b}=(e^{operatorname {ln} (r)+i(theta +2pi k)})^{b}=e^{b(operatorname {ln} (r)+i(theta +2pi k))}.}$

Здесь — комплексный логарифм, — его главное значение.

При этом комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно^[8]. Неучёт этого обстоятельства может привести к ошибкам. Пример: возведём известное тождество ${displaystyle e^{2pi i}=1}$ в степень Слева получится ${displaystyle e^{-2pi },}$ справа, очевидно, 1. В итоге: ${displaystyle e^{-2pi }=1,}$ что, как легко проверить, неверно. Причина ошибки: возведение в степень даёт и слева, и справа бесконечное множество значений (при разных ), поэтому правило ${displaystyle left(a^{b}right)^{c}=a^{bc}}$ здесь неприменимо. Аккуратное применение формул определения комплексной степени даёт слева и справа ${displaystyle e^{-2pi k};}$ отсюда видно, что корень ошибки — путаница значений этого выражения при k=0 и при

Степень как функция[править | править код]

Разновидности[править | править код]

Поскольку в выражении $x^{y}$ используются два символа ( и ), то его можно рассматривать как одну из трёх функций.

Ноль в степени ноль[править | править код]

Выражение $0^{0}$ (ноль в нулевой степени) многие учебники считают неопределённым и лишённым смысла, поскольку, как указано выше, функция ${displaystyle f(x,y)=x^{y}}$ в точке (0, 0) разрывна. Некоторые авторы предлагают принять соглашение о том, что это выражение равно 1. В частности, тогда разложение в ряд экспоненты:

${displaystyle e^{x}=1+sum _{n=1}^{infty }{x^{n} over n!}}$

можно записать короче:

${displaystyle e^{x}=sum _{n=0}^{infty }{x^{n} over n!}.}$

Следует предостеречь, что соглашение 0^0=1 чисто символическое, и оно не может использоваться ни в алгебраических, ни в аналитических преобразованиях из-за разрывности функции в этой точке.

История[править | править код]

Обозначение[править | править код]

В Европе сначала степень величины записывали словесными сокращениями (q или Q обозначало квадрат, c или C — куб, bq или qq — биквадрат, то есть 4-я степень и т. д.) или как произведение — например, $x^{4}$ изображалось как Отред записывал ${displaystyle x^{5}-15x^{4}}$ следующим образом: (если неизвестная всего одна, ей часто не присваивался буквенный значок)^[9]. Немецкая школа коссистов для каждой степени неизвестной предлагала особый готический значок.

В XVII веке постепенно стала преобладать идея явно указывать показатель степени. Жирар (1629 год) для возведения в степень числа ставил показатель в круглых скобках перед этим числом, а если числа правее показателя не было, то это значило, что подразумевается наличие неизвестного в указанной степени^[10]; например, у него означало ${displaystyle 2^{2}+x^{2}}$ . Варианты размещения показателя степени предлагали Пьер Эригон и шотландский математик Джеймс Юм, они записывали $x^{4}$ в виде и ${displaystyle x^{IV}}$ соответственно^[11].

Современная запись показателя степени — правее и выше основания — введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2 (возведение в квадрат ещё долгое время обозначалось по-старому, произведением). Позднее Валлис и Ньютон (1676) распространили декартову форму записи степени на отрицательные и дробные показатели, трактовка которых к этому времени уже была известна из трудов Орема, Шюке, Стевина, Жирара и самого Валлиса. К началу XVIII столетия альтернативы для записи степеней «по Декарту», как выразился Ньютон в «Универсальной арифметике», «вышли из моды» (out of fashion). Показательная функция, то есть возведение в переменную степень, появилась сначала в письмах, а потом и в трудах Лейбница (1679). Возведение в мнимую степень обосновал Эйлер (1743)^[11]^[12].

Запись возведения в степень в языках программирования[править | править код]

С появлением компьютеров и компьютерных программ возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень в «двухэтажном» виде. В связи с этим изобрели особые значки для обозначения операции возведения в степень. Первым таким значком были две звёздочки: «**», используемые в языке Фортран. В появившемся несколько позже языке Алгол использовался значок стрелки: «↑» (стрелки Кну́та). В языке Бейсик предложен символ «^» («циркумфлекс», он же «карет»), который приобрёл наибольшую популярность; его часто используют при написании формул и математических выражений не только в языках программирования и компьютерных системах, но и в простом тексте. Примеры:

3^2 = 9; 5^2 = 25; 2^3 = 8; 5^3 = 125.

Иногда в компьютерных системах и языках программирования значок возведения в степень имеет левую ассоциативность, в отличие от принятого в математике соглашения о правой ассоциативности возведения в степень.
То есть некоторые языки программирования (например, программа Excel) могут воспринимать запись a^b^c, как (a^b)^c, тогда как другие системы и языки (например, Haskell, Perl, Wolfram|Alpha и многие другие) обработают эту запись справа налево: a^(b^c), как это принято в математике: ${displaystyle a^{b^{c}}=a^{left(b^{c}right)}}$ .

Некоторые знаки возведения в степень в языках программирования и компьютерных системах:

x ↑ y: Алгол, некоторые диалекты Бейсика;
x ^ y: Бейсик, J, MATLAB, R, Microsoft Excel, TeX, bc^{[К 2]}, Haskell^{[К 3]}, Lua, MathML и большинство систем компьютерной алгебры;
x ^^ y: Haskell^{[К 4]}, D;
x ** y: Ада, Bash, Кобол, Фортран, FoxPro, Gnuplot, OCaml, Perl, PL/I, PHP^{[К 5]}, Python, REXX, Ruby, SAS, Seed7, Tcl, ABAP, Haskell^{[К 6]}, Turing^[en], VHDL, ECMAScript^{[К 7]}^{[К 8]}, AutoHotkey^{[К 8]}, JavaScript;
x⋆y: APL.

Во многих языках программирования (например, в Java, Си и Паскале) отсутствует операция возведения в степень, и для этой цели используют стандартные функции.

Вариации и обобщения[править | править код]

Возведение в степень с натуральным показателем можно определить не только для чисел, но и для нечисловых объектов, для которых определено умножение — например, к матрицам, линейным операторам, множествам (относительно декартова произведения, см. декартова степень).

Обычно эта операция рассматривается в некотором мультипликативном моноиде (полугруппе с единицей) и определяется индуктивно^[13] для любого xin M :

Особенную ценность представляет применение возведения в степень к группам и полям, где возникает прямой аналог отрицательных степеней.

Гипероператор возведения в степень — тетрация.

Примечания[править | править код]

↑ ¹ ² Степень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 221.
↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции / Пер. с голл. И. Н. Веселовского. — М., 1959. — С. 165—167. — 456 с.
↑ Справочник по элементарной математике, 1978, с. 140—141.
↑ ¹ ² Справочник по элементарной математике, 1978, с. 182—184.
↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
↑ Пискунов Н. С. § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа. scask.ru. Дата обращения: 27 марта 2022.
↑ Близняков Н.М. КОМПЛЕКСНЫЕ ЧИСЛА. Учебно-методическое пособие для вузов 23. Дата обращения: 27 марта 2022. Архивировано 1 апреля 2022 года.
↑ ¹ ² ³ Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — С. 597 (подстрочное примечание 3). — 872 с.
↑ History of Mathematical Notations, vol. 1, 2007, §290—297.
↑ History of Mathematical Notations, vol. 1, 2007, §164.
↑ ¹ ² Александрова Н. В., 2008, с. 130—131.
↑ History of Mathematical Notations, vol. 1, 2007, §298—301, 307—309.
↑ David M. Bloom. Linear Algebra and Geometry (англ.). — 1979. — P. 45. — ISBN 978-0-521-29324-2.

Комментарии

↑ В разговорной речи иногда говорят, например, что ${displaystyle a^{3}}$ — «a умноженное само на себя три раза», имея в виду, что берётся три множителя . Это не совсем точно и может привести к двусмысленности, так как количество операций умножения будет на одну меньше: ${displaystyle a^{3}=acdot acdot a}$ (три множителя, но две операции умножения). Часто, когда говорят «a умноженное само на себя три раза», имеют в виду количество умножений, а не множителей, то есть ${displaystyle a^{4}.}$ См. Август Давидов. Начальная алгебра. — Типографія Э. Лисслер и Ю. Роман, 1883-01-01. — С. 6. — 534 с. Архивная копия от 31 мая 2016 на Wayback Machine. Чтобы избежать двусмысленности, можно говорить, к примеру: третья степень — это когда «число три раза входит в умножение».
↑ Для целой степени.
↑ Для неотрицательной целой степени.
↑ Поддерживает отрицательные степени, в отличие от ^, реализованной только как последовательное умножение.
↑ Начиная с версии 5.6 (см. Руководство по PHP › Appendices › Миграция с PHP 5.5.x на PHP 5.6.x › Новые возможности Архивная копия от 18 апреля 2018 на Wayback Machine).
↑ Для степени, представленной числом с плавающей запятой — реализовано через логарифм.
↑ Описан в стандарте EcmaScript 7 (ECMA-262, 7th edition), принятом в июне 2016 года.
↑ ¹ ² В JavaScript изначально присутствует метод Math.pow(x, y).

Литература[править | править код]

Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — 509 с.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 стр.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Степенная функция // Большая советская энциклопедия. — М.: Советская энциклопедия, 1969—1978.
Cajori F. A History of Mathematical Notations. Vol. 1 (1929 reprint). — NY: Cosimo, Inc., 2007. — xvi + 456 p. — ISBN 978-1-60206-684-7.

Ссылки[править | править код]

Возведение в степень: правила, примеры. Дата обращения: 2 февраля 2020.

Источник

При помощи нашего калькулятора вы легко сможете возвести число в любую степень.

Что же такое возведение числа в степень? Для того, что бы это понять давайте с вами разберем простой пример:

4³

из которых 4 – это основание, 3 – степень в которую необходимо возвести основание.
Решение данной задачи состоит в следующем

4*4*4 = 64.

Таким образом мы можем сделать простой вывод возведение числа в степень это умножение этого числа на само себя столько раз в какой степени он находиться.

Возводить можно не только в положительную степень, но и в отрицательную. Многие задаются вопросом как возвести в отрицательную степень. При возведении в отрицательную степень надо как обычно возвести число в степень и разделить на него единицу.
Таким образом выражение

4^-3

Записывается следующим образом

1/(4*4*4)= 1/64 = 0,015625

Источник

Степень числа, говоря простым языком – это то, сколько раз число последовательно умножили само на себя. Например, если мы хотим вычислить, чему будет равно число 2, возведенное в степень 4, то нам нужно число 2 перемножить само на себя 4 раза (2х2х2х2). В результате мы получи 16.

источник: Яндекс

Число 2 здесь будет называться основание степени, а число 4, стоящее над двойкой – показателем. Правильно читается, как «два в степени четыре».

источник: Яндекс

В степень можно возводить и положительные и отрицательные числа, с одной лишь разницей – положительное число, после возведения в степень, всегда останется положительным. Результат возведения в степень отрицательного числа, в свою очередь, будет зависеть от того, четной или нечетной была степень. Так (-2) в четвертой степени будет равняться 16, а (-2) в пятой степени будет равно (-32).

Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф

Каждый раз высчитывать, чему равно число в некой степени, перемножая его вручную, крайне муторно. Куда проще воспользоваться таблицей степеней.

источник: Яндекс

Это таблица степеней, показывающая результат возведения чисел от 1 до 10 в степени от 1 до 10. Пользоваться ей очень удобно. Нужно найти пересечение нужного числа и степени, и в этой точке будет написан результат возведения.

Ускоренное возведение в степень

Но что делать, если под рукой нет таблицы, и воспользоваться калькулятором тоже нет возможности? Существует достаточно простой алгоритм, который упростит вычисления. Предположим, что нам надо узнать, сколько будет 3 в степени 15. Для этого мы:

Показатель степени раскладываем на сумму степеней с основанием 2. 15 – это 1+2^1+2^2+2^3, то есть 1+2+4+8.
Затем последовательно возводим основание 3 в степени, получившиеся при разложении показателя степени. Это (3^1)x(3^2)x(3^4)x(3^8).
Наконец, считаем результат. 3^1=3, 3^2=9, с этим все просто. Зная что, 3 в степени 2 равняется 9, легко вычислить, чему будет равно 3 в степени 4. Это (3^2)x(3^2), то есть 9х9, получается 81. Так же поступаем и с вычислением 3^8. Зная, что 3^4=81, для вычисления 3^8 перемножаем 81 и 81, получаем 6561. Теперь нужно вычислить результат 3х9х81х6561. Получаем 14 348 907.

Так или иначе, все равно придется производить сложные вычисления, но так вы сократите количество производимых умножений. В данном случае 6 операций умножения, взамен 15-кратного перемножения тройки саму на себя.

Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!

Источник

В статье мы введём понятие степени числа, на простых и понятных примерах объясним, что такое степень с целым показателем, натуральным, рациональным, действительным и иррациональным. Заодно покажем несколько поучительных примеров и задач, которые помогут читателю лучше понять и полнее уяснить тему.

Степень с натуральным показателем

Определение 1 + формула

Степенью числа a с натуральным показателем n называют число, полученное в результате умножения числа a самого на себя n количество раз. В виде формулы выше сказанное можно записать так:

[a^{n}=aa ldots * a]

Читается запись, как «a» в степени «n». Для a² и для a³ можно сказать «a в степени два» и «a в степени три» или «a во второй степени» и «a в третьей степени». Однако гораздо чаще говорят: «a в квадрате» и «a в кубе». Это устоявшиеся, общеупотребительные названия. Например, «3 в квадрате» или «7 в кубе». Формулировки типа «3 в степени два» и «7 в степени три» ошибочными не считаются, но употребляются гораздо реже, a называется основанием степени.

Запомните, n обозначает количество множителей, то, сколько раз a нужно само на себя перемножить.

Примеры 1 — 6

4⁷ читается, как «четыре в седьмой степени». В виде произведения 4⁷ может быть записано, как 4*4*4*4*4*4*4. При этом 4 является основанием, а 7 её показателем.

19³. Может быть прочтено, как «19 в кубе». Оба прочтения будут одинаково верными.

(8,234)⁵.Читается, как «8,234 в пятой степени». Обратите внимание, в данном случае основанием является десятичная дробь.

(2/5)⁹. Здесь основанием будет обычная дробь, она правильная.

(43/7)³ тоже отвечает определению. Из указанного примера видно, что основанием может быть и не правильная дробь.

Записи (8(3/7))⁸, (-5/9)⁵. (√3)⁷, (-√8)² есть степени с целым n. Однако надо понимать разницу между (-5)³ и –5³. Первое является степенью отрицательного числа, а второе можно записать как –(5³). Оно соответствует числу, которое противоположно 5³.

Отдельно рассмотрим пример, когда n равен 1. Любое число с ним можно записать в виде a¹. Некоторые почему-то считают, что этом случае следует выполнить умножение столько раз, сколько указано в показателе. На самом деле ничего умножать не нужно. Степень любого числа с n равным 1 будет самим этим числом.

Т. е. 56¹ = 56, (1/456)¹ равно 1/456, (-86)¹ равно -86.

Запись 0ⁿ тоже имеет право на существование. По сути она означает, что нуль нужно помножить на себя самого n раз. Умножение на нуль всегда даёт нуль. Получается, любая степень с основанием нуль, независимо от её показателя всегда будет равна нулю.

Значительно реже всех выше перечисленных случаев встречается запись типа a^n. Она соответствует записи aⁿ.

Примеры 7 — 9

9^8 читается, как «9 в восьмой степени», n может быть и многозначным числом.

5^(237). Читается, как «5 в двести тридцать седьмой степени».

Выражения 7^8,4, (3/56)^1/2, 8^√3 не являются степенями с натуральным показателем.

Запомните, основанием степени с натуральным n может быть практически любое число (хоть дробь, хоть корень и т. д.), а вот в показателе должно обязательно находиться натуральное число, т. е. не дробное и не отрицательное.

Основные свойства степени с натуральным показателем

Они следующие:

Когда происходит умножение степеней с равным основанием, то оно остаётся прежним. Показатели при этом складываются.
a^m*aⁿ = a^m+n

Когда степени с одинаковыми основаниями делятся, то основание сохраняется прежним, а показатели вычитаются.
a^m/aⁿ = a^m-n При этом m > n и a не равно нулю.

Когда степень возводят в степень, то основание не меняют, а сами степени перемножаются.
(a^m)ⁿ = a^m*n

Если в степень возводится дробь, то в неё возводится как числитель дроби, так и её знаменатель.
(a/b)ⁿ = aⁿ/bⁿ При этом b не должно быть равно нулю.

Примеры 10 — 12

2¹*2²*2³. Складываем 1, 2 и 3. В итоге 2¹⁺²⁺³=2⁶

(-3/7)⁵: (-3/7)³. Из 5 вычитаем 3. В результате имеем (-3/7)^5-3 = (-3/7)².

Нужно возвести в степень выражение (a²*b³)⁴. Сначала на 4 умножаем 2, затем 3. Итогом будет выражение a⁸b¹².

О сравнении степеней

Если сравниваемые степени имеют равные основания, большие числа 1, то большим считается та из них, у которой показатель степени выше.

Примеры 13 — 16

Какое из чисел больше: 2¹⁷ или 2²⁷. Основания одинаковые, но 27 больше, чем 17. 27>17. Значит 2²⁷ больше, чем 2¹⁷.

Если n одинаковые, но основание находится в промежутке от 0 до 1, то большим будет степень, у которой показатель меньше.

Сравнить числа (0,3)¹¹и (0,3)⁷. Основание больше ноля, но не доходит до единицы. Значит, в отличие от предыдущего примера, здесь всё наоборот. Большим будет считаться число, с меньшим показателем. Т. к. 11>7, то (0,3)¹¹<(0,3)⁷.

Если n одинаковые, а основания разные, то большим будет то, у которого больше основание.

Сравнить между собой числа 7³ и 15³. 15 >7, значит 15³ больше, чем 7³.

Если различаются и показатели, и основания, то числа, посредством тех или иных преобразований, сначала приводят к вида, когда у них либо то, либо другое одинаково, а уже потом сравнивают по приведённым выше правилам.

Выясните, какое из чисел больше 3²⁰⁰ или 2³⁰⁰.

2³⁰⁰ = 2^3*100 = (23)¹⁰⁰ =8¹⁰⁰

3²⁰⁰ = 3^2*100 = (32)¹⁰⁰ = 9¹⁰⁰

9 больше, чем 8. Значит 9¹⁰⁰ больше 8¹⁰⁰.

Соответственно 3²⁰⁰ будет больше, чем 2³⁰⁰.

Степень с целым показателем

Определение 2

Степенью с целым показателем называется степень, показателем которой является любое целое число. Это своего рода расширение множества чисел с натуральным показателем. К последним прибавляются числа с отрицательным значением и ноль.

Рассмотрим степень с целым отрицательным n. Любое число вида a^-n можно представить в виде 1/aⁿ. При этом a не должно быть равно нулю. n может быть любым натуральным числом.

Примеры 17 — 18

7^-5 не является степенью с натуральным показателем, но в то же самое время является степенью с целым показателем. Примечательно, что равное ему число (1/7)⁵ будет степенью с целым n. Мы рассматриваем 7^-5 и (1/7)⁵, как равные, но, всё-таки, разные числа.

(4/5)^-1 можно представить как 1/(4/5)¹.

Сложнее дело обстоит с понятием нулевой степени. Чтобы её объяснить, ещё раз приведём правило по делению степеней с равными основаниями.

Правило 1

Равенство a^m/aⁿ = a^m-n остаётся верным лишь в том случае, когда m и n будут натуральными числами, m < n и a не равно нулю. Последнее условие позволяет нам избежать деления на нуль. Если m и n окажутся равными, то мы придём к результату (aⁿ/aⁿ) = a^n-n = a⁰

Т. е. при делении степеней, которые имеют одно и тоже основание из показателя делимого следует вычесть n делителя. В случае, когда и они одинаковы, например, если a³ разделить на a³, мы получим a⁰.

Как известно из курса элементарной математики, частное от деления любого числа на самого себя всегда равно единице. Из этого напрямую следует, что нулевая степень любого числа всегда равна 1.

Пример 19

7⁰= 1, -5⁰= 1, (3/5)⁰ = 1, (√8)⁰ = 1, (7567776)⁰ = 1.

Несколько неожиданным для многих является тот факт, что ноль в степени ноль тоже равен единице 0⁰ = 1. Положение осложняет тот факт, что на ноль делить нельзя. Так откуда же тогда взяли, что нулевая степень нуля есть 1.

На самом деле, хотя на ноль никакое число не делится, оно может делится на сколь угодно малое, т. е. близкое к нулю число. В высшей математике доказывается, что предел (a/a), когда a является бесконечно малой величиной, действительно стремится к 1.

Свойства степени с целым показателем практически ничем не отличаются от её свойств с натуральным. Нужно только помнить, что в показателе появляются отрицательные числа и их следует складывать и вычитать по строго определённым для этого правилам.

Примеры 20 — 21

5⁷* 5^-3= 5^7-3 = 5⁴.

8⁴/8^-2 = 8^4-(-2)= 8⁶.

Нет времени решать самому?

Наши эксперты помогут!

Степень с рациональным показателем

Определение 3

Степенью с рациональным показателем называется степень, показатель которой, есть рациональное число, т. е. помимо целых и отрицательных значений, может иметь ещё и дробные. Записывается это в виде a^m^/ⁿ. Из определения дробной степени известно, что a^m^/ⁿ можно записать в виде ⁿ√a^m. n не должно быть равно нулю, ведь на ноль делить нельзя.

Если m и n делятся нацело, то получаем степень с целым показателем. Если при этом ещё и частное от деления больше нуля, то получим степень с натуральным.

Правило 2

Любое число a^m^*^k^/ⁿ^*^k можно заменить на a^m^/ⁿ.

Теперь о том, почему в дроби требуется замена сократимого показателя на несократимый. Если этого не делать, то может возникнуть, например, следующая ситуация:

(-1)^6/10 = (-1)^2/5, однако, если посчитать получится

(-1)^6/10 = ¹⁰√(-1)⁶ = ¹⁰√1 = 1.

(-1)^3/5 = ⁵√(-1)³ = ⁵√(-1) = -1

Примеры степеней с рациональным n: (3^1/2), 7^5/4, 7^4/2. Основание может быть и многозначным числом, в частности, 128^-2/7 тоже степень с рациональным.

Примеры 22 — 24

-16^1/4 является степенью с рациональным показателем.

(-16)^1/4 смысла не имеет. Оно равносильно выражению ⁴√(-16). Какое число нужно возвести в четвёртую степень, чтобы получить -16 ? Ответ – никакое. Такого числа не существует.

Казалось бы, √(-8) имеет право на существование. Оно равно -2 И действительно, можно записать (-8)^1/3= -2. Однако, если мы запишем 1/3.

по-другому, то результат окажется совершенно иным. Смотрите:

(-8)^1/3 = (-8)^2/6 = ⁶√(-8)² = ⁶√(64) = 2.

Получается парадокс, поэтому запись √(-8) лишено смысла.

Из примеров выше становится ясно, что извлечение чётных корней из отрицательных чисел категорически запрещено.

Не будет ошибкой замена любого из дробных показателей смешанным (например, 5^2,1 на 5^2(1/10), однако, чтобы не запутаться, при проведении вычислений, всегда, когда это возможно, лучше заменяйте подобные числа и корень числа дробной степенью. Это делает запись более наглядной и позволяет избежать многих ошибок.

Свойства степени с рациональным показателем аналогичны с натуральным или целым n, только дело приходится иметь с дробями. В первую очередь это касается деления и перемножения степеней с одинаковыми основаниями, а также их сравнения. Вспомните, как оно проводится для обыкновенных дробей.

пример 25

7^2/3 * 7^8/4= 7^32/12 = 7^16/6

Степень числа с иррациональным показателем

Чтобы разобраться в этом вопросе, нужно разобраться в том, что является иррациональным числом. Любое рациональное число допускает его представление в виде бесконечной периодической десятичной дроби либо как обыкновенную дробь типа (m/n). Об иррациональных числах этого не скажешь. Десятичные дроби, с помощью которых выражаются иррациональные числа, бесконечны и апериодичны. Примерами иррациональных чисел являются √7, число [pi], √2 + √3.

Строится степень с рациональным n с помощью так называемого предельного перехода по последовательностям степеней с рациональными показателями. Они с недостатком либо с избытком приближаются к степени иррациональным n.

Покажем как это происходит. Пусть нам дано иррациональное число a.

a0 = 1,6 , a1 = 1,67, a2 = 1,671…

a0 = 1,67, a1 = 1,6717, a2 = 1,671753…

И т. д. Заметьте – сами приближения, это рациональные числа.

Последовательности приближений нам нужно поставить в соответствие последовательность степеней α^a⁰, α^a¹, α^a². Значения этих степеней можно подсчитать.

a = 1,67175331. Пусть для примера у нас будет α = 3

Тогда получается α^a⁰ = 3,167; α^a¹ = 3,16717; α^a²= 3,1671753 и т. д.

Указанная последовательность сводится к числу, которое окажется значением степени с основанием α и иррациональным показателем a. После некоторой работы в итоге получаем 3^1,67175331 = 6,27.

Свойства у степени с иррациональным n в целом такие же, как рациональным. В частности, сложение показателей при перемножении, сравнение иррациональных степеней происходят аналогичным образом. Нужно только иметь в виду, что при бесконечности и апериодичности иррациональной дроби вы имеете дело с приближёнными с той или иной точностью значениями. Впрочем, в зависимости от поставленной задачи, нужной точности достичь можно в любом случае. Очень осторожны будьте с приближениями. У новичков здесь очень часто случаются ошибки. После некоторого опыта и практики действия совершаются автоматически. Старайтесь на первых порах порешать как можно больше примеров. Пусть они кажутся вам однотипным, но навык отточить и закрепить позволяют.

Источник

Понятие возведения в степень

Как возвести число в натуральную степень

Как возвести число в целую степень

Как возвести число в дробную степень

Как возвести число в иррациональную степень

Возведение степени в степень

Употребление в устной речи[править | править код]

Свойства[править | править код]

Основные свойства[править | править код]

Таблица натуральных степеней небольших чисел[править | править код]

Расширения[править | править код]

Целая степень[править | править код]

Рациональная степень[править | править код]

Вещественная степень[править | править код]

Комплексная степень[править | править код]

Степень как функция[править | править код]

Разновидности[править | править код]

Ноль в степени ноль[править | править код]

История[править | править код]

Обозначение[править | править код]

Запись возведения в степень в языках программирования[править | править код]

Вариации и обобщения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Ускоренное возведение в степень

Степень с натуральным показателем

[a^{n}=a*a* ldots * a]

Основные свойства степени с натуральным показателем

О сравнении степеней

Степень с целым показателем

Степень с рациональным показателем

Степень числа с иррациональным показателем

Вам также может понравиться

Как найти 2019 к 2018 году

Плохая покраска авто как исправить

Как составить предложение к слову эскимо

Добавить комментарий Отменить ответ

[a^{n}=aa ldots * a]