Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = – 5.
Решение:
При b = – 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения – это выражения, отличающиеся только знаками. Например,
и
и
– сопряженные выражения.
Пример:
12. Вот несколько примеров – как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: – 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях – в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Что такое корень n-й степени из действительного числа
Чтобы научиться работать с корнями степени (n), необходимо знать, что такое арифметический КВАДРАТНЫЙ корень и его свойства.
Корнем n-й степени ((n=2, 3, 4, 5, 6… )) некоторого числа (a) называют такое неотрицательное число (b), которое при возведении в степень (n in N) дает (a). Корень n-ой степени обозначается при помощи знака радикала (sqrt[n]{a}):
$$ sqrt[n]{a}=b; $$
$$ b^{n}=underbrace{b*b*b*…*b}_{n ; раз}=a. $$
Число (n in N) при этом называют показателем корня, а число (a) покоренным выражением.
Если (n=2), то перед вами корень 2-й степени или обычный арифметический квадратный корень, который все проходили в 8-м классе.
Если (n=3), то это корень 3-й степени, (sqrt[3]{a}). Его обычно называют кубическим корнем. Чтобы его вычислить, нужно найти такое число, которое умноженное на само себя три раза, даст подкоренное выражение.
Если (n=4), то корень 4-й степени, (sqrt[4]{a}) и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень. Для того, чтобы вычислить корень n-й степени от (a), нужно сообразить какое число в степени (n) будет давать (a).
Пример 1
$$ sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2
$$ sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3
$$ sqrt[n]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4
$$ sqrt[n]{1}=1 $$
Если извлечь корень n-й степени из 1, всегда будет 1.
Пример 5
$$ sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим (2,668…) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть (sqrt[3]{19}).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева ближайшие числа, корень из которых посчитать можно:
$$ sqrt[3]{8} le sqrt[3]{19} le sqrt[3]{27} $$
$$ 2 le sqrt[3]{19} le 3 $$
Получается, что наш корень лежит между числами 2 и 3.
Пример 6
Оценить значение (sqrt[4]{15}= ?)
$$ sqrt[4]{1} le sqrt[4]{15} le sqrt[4]{16}; $$
$$ 1 le sqrt[4]{15} le 2; $$
Корень четной и нечетной степеней
Надо четко различать правила работы c четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из неотрицательного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 7
$$ sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного. Напоминаю, что извлечь корень 3-й степени, значит найти такое число, которое при возведении в 3-ю степень даст покоренное выражение. Если ((-3)) умножить на само себя три раза, то мы получим покоренное выражение (-27=(-3)*(-3)*(-3)).
Пример 8
$$ sqrt[4]{-27} $$
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. Невозможно найти число, которое при умножении на само себя четыре раза, даст отрицательное значение.
Из-под знака нечетного показателя корня можно выносить минус. Это упрощает процесс подсчета.
$$sqrt[5]{-32}=-sqrt[5]{32}=-2;$$
Свойства корня n-й степени
Пусть есть два числа a и b, для них будут выполняться следующие свойства:
$$ (sqrt[n]{a})^n=a $$
$$ sqrt[n]{a^n}=a $$
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
$$ (sqrt[n]{a})^k=sqrt[n]{a^k} $$
$$sqrt[n] {sqrt[k]{a}}=sqrt[n*k]{a} $$
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
При использовании вышеперечисленных свойств важно помнить: корень четной степени не существует из отрицательных чисел, и сам корень четной степени всегда положителен. Надо быть внимательным и следить, чтобы в ходе преобразований эти ограничения не нарушались.
Рассмотрим примеры на свойства корня степени (n).
Пример 9
$$(sqrt[5]{7})^5=7;$$
При возведении корня с показателем (n) в степень (n) остается просто подкоренное выражение, так как возведение в степень и извлечение корня это взаимно обратные операции.
Обратите внимание, что неважно, где стоит степень – над корнем или под корнем, результат будет одинаковым.
$$sqrt[5]{7^5}=7$$
Из рассмотренного выше примера следует свойство ((sqrt[n]{a})^k=sqrt[n]{a^k}). Не имеет значения, извлекаете ли вы сначала корень, а потом возводите в степень, или наоборот, сначала возводите в степень подкоренное выражение, и только потом извлекаете корень.
Пример 10
$$sqrt[3]{8^2}=(sqrt[3]{8})^2=2^{2}=4;$$
$$sqrt[3]{8^2}=sqrt[3]{64}=4;$$
Получается одно и тоже.
Более того, показатель корня и степень подкоренного выражения можно домножить на одно и тоже число (p), результат от этого не изменится. Может пригодиться в различных преобразованиях и при сравнении корней между собой.
$$ sqrt[n]{a^k}=sqrt[n*p]{a^{k*p}};$$
Пример 11
$$ sqrt[3]{10^2}=sqrt[3*2]{10^{2*2}}=sqrt[6]{10^{4}}=sqrt[6]{1000};$$
Эту же формулу можно использовать наоборот:
$$ sqrt[n*p]{a^{k*p}}=sqrt[n]{a^k} $$
То есть можно сокращать показатель корня и степень подкоренного выражения, что существенно упрощает вычисления в некоторых случаях.
Пример 12
$$ sqrt[6]{16}=sqrt[6]{2^4}=sqrt[3]{2^2}=sqrt[3]{4};$$
Рассмотрим применение формул корня от произведения и частного, без которых невозможно решить ни один приличный пример.
Корень степени (n) от произведения равен произведению корней степени (n) от этих множителей.
$$ sqrt[n]{a*b}=sqrt[n]{a}*sqrt[n]{b} $$
И аналогично корень степени (n) от частного равен частному корней n-й степени.
$$ sqrt[n]{frac{a}{b}}=frac{sqrt[n]{a}}{sqrt[n]{b}}, b neq 0 $$
Пример 13
$$sqrt[3]{125*8}=sqrt[3]{125}*sqrt[3]{8}=5*2=10;$$
$$sqrt[3]{-frac{27}{8}}=frac{-sqrt[3]{27}}{sqrt[3]{8}}=frac{-3}{2};$$
Формулы справедливы не только для двух множителей:
Пример 14
$$sqrt[3]{125*8*27}=sqrt[3]{125}*sqrt[3]{8}*sqrt{27}=5*2*3=30;$$
Пример 15
$$sqrt[4]{frac{16*81}{625}}=frac{sqrt[4]{16*81}}{sqrt[4]{625}}=frac{sqrt[4]{16}*sqrt[4]{81}}{sqrt[4]{625}}=frac{2*3}{5}=frac{6}{5};$$
Обратите внимание! Формулы произведения и частного корней справедливы только для корней с одинаковыми показателями. Нельзя перемножить корни с разными показателями.
$$sqrt[3]{6}*sqrt[4]{7}=?$$
Ничего здесь сделать мы не можем!
И следите за отрицательными числами при использовании корней четной степени. Произведение двух отрицательных чисел может существовать под одним корнем, так как они при умножении дают знак плюс. Но разбивать такое произведение на два корня четной степени ни в коем случае нельзя: выражение теряет всякий смысл.
$$sqrt[4]{-15*(-7)} neq sqrt[4]{-15}*sqrt[4]{-7};$$
$$sqrt[4]{-15*(-7)} = sqrt[4]{15*7}=sqrt[4]{15}*sqrt[4]{7};$$
Часто преобразование и упрощение математических выражений требует перехода от корней к степеням и наоборот. Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.
Переход от степеней с дробными показателями к корням
Допустим, мы имеем число с показателем степени в виде обыкновенной дроби – amn. Как записать такое выражение в виде корня?
Ответ вытекает из самого определения степени!
Положительное число a в степени mn – это корень степени n из числа am.
amn=amn.
При этом, обязательно должно выполнятся условие:
a>0; m∈ℤ; n∈ℕ.
Дробная степень числа нуль определяется аналогично, однако в этом случае число m принимается не целым, а натуральным, чтобы не возникло деления на 0:
0mn=0mn=0.
В соответствии с определением, степень amn можно представить в виде корня amn.
Например: 325=325, 123-34=123-34.
Однако, как уже было сказано, не следует забывать про условия: a > 0 ; m ∈ ℤ ; n ∈ ℕ .
Так, выражение -813 нельзя представить в виде -813, так как запись -813 попросту не имеет смысла – степень отрицательных чисел на определена.При этом, сам корень -813 имеет смысл.
Переход от степеней с выражениями в основании и дробными показателями осуществляется аналогично на всей области допустимых значений (далее – ОДЗ) исходных выражений в основании степени.
Например, выражение x2+2x+1-412 можно представить в виде квадратного корня x2+2x+1-4.Выражение в степени x2+x·y·z-z3-73 переходит в выражение x2+x·y·z-z3-73 для всех x, y, z из ОДЗ данного выражения.
Как представить корень в виде степени?
Обратная замена корней степенями, когда вместо выражения с корнем записывается выражения со степенью, также возможна. Просто перевернем равенство из предыдущего пункта и получим:
amn=amn
Опять же, переход очевиден для положительных чисел a. Например, 764=764, или27-53=27-53.
Для отрицательных a корни имеют смысл. Например -426, -23. Однако, представить эти корни в виде степеней -426 и -213 нельзя.
Можно ли вообще преобразовать такие выражения со степенями? Да, если произвести некоторые предварительные преобразования. Рассмотрим, какие.
Используя свойства степеней, можно выполнить преобразования выражения -426.
-426=-12·426=426.
Так как 4>0, можно записать:
426=426.
В случае с корнем нечетной степени из отрицательного числа, можно записать:
-a2m+1=-a2m+1.
Тогда выражение -23 примет вид:
-23=-23=-213.
Разберемся теперь, как корни, под которыми содержатся выражения, заменяются на степени, содержащие эти выражения в основании.
Обозначим буквой A некоторое выражение. Однако не будем спешить с представлением Amn в виде Amn. Поясним, что здесь имеется в виду. Например, выражение х-323, основываясь на равенстве из первого пункта, хочется представить в виде x-323. Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.
Таким образом, в рассмотренном примере преобразование вида Amn=Amn является преобразованием, сужающим ОДЗ, а из-за неаккуратного применения формулы Amn=Amn нередко возникают ошибки.
Чтобы правильно перейти от корня Amn к степени Amn, необходимо соблюдать несколько пунктов:
- В случае, если число m – целое и нечетное, а n – натуральное и четное, то формула Amn=Amn справедлива на всей ОДЗ переменных.
- Если m – целое и нечетное, а n – натуральное и нечетное,то выражение Amn можно заменить:
– на Amn для всех значений переменных, при которых A≥0;
– на –Amn для для всех значений переменных, при которых A<0; - Если m – целое и четное, а n – любое натуральное число, то Amn можно заменить на Amn.
Сведем все эти правила в таблицу и приведем несколько примеров их использования.
Вернемся к выражению х-323. Здесь m=2 – целое и четное число, а n=3 – натуральное число. Значит, выражение х-323 правильно будет записать в виде:
х-323=x-323.
Приведем еще один пример с корнями и степенями.
x+5-35=x+5-35, x>-5–x-5-35, x<-5
Обоснуем результаты, приведенные в таблице. Если число m – целое и нечетное, а n – натуральное и четное, для всех переменных из ОДЗ в выражении Amn значение A положительно или неотрицательно (при m>0). Именно поэтому Amn=Amn.
Во втором варианте, когда m – целое, положительное и нечетное, а n – натуральное и нечетное, значения Amn разделяются. Для переменных из ОДЗ, при которых A неотрицательно, Amn=Amn=Amn. Для переменных, при которых A отрицательно, получаем Amn=-Amn=-1m·Amn=-Amn=-Amn=-Amn.
Аналогично рассмотрим и следующий случай, когда m – целое и четное, а n – любое натуральное число. Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.
Таким образом, в третьем случае для всех переменных из ОДЗ можно записать Amn=Amn.
{2}]
Степень корня указывается над знаком корня слева. [sqrt[x]{a}], в данном примере х — степень. Если запись не имеет такого обозначения, значит перед нами корень квадратный.
Умножение корней
Существует несколько вариантов умножения корней, это умножение с множителем, без множителя и с разными показателями.
Умножение без множителей
Первым делом рассмотри, как умножаются корни без множителя.
Убедившись, что корни, с которыми необходимо произвести действие имеют одинаковые степени. Например квадратный корень из числа а, можно умножать на квадратный корень из d.
Рассмотрим правило на двух примерах произведения двух квадратных и двух кубических корней.
Примеры:
[sqrt{2} * sqrt{6}=] первый пример умножение квадратных корней.
[sqrt[3]{3} * sqrt[3]{18}=] второй пример умножение кубических корне.
Решение:
Для того чтобы решить данные примеры необходимо произвести умножение под корнем. {2} * 3}=2 sqrt{3}], в данном примере число 12 можно разложить на произведение чисел 4 и 3, где 4 равно двум в квадрате. Поэтому 2 выносим за приделы корня и упрощаем выражение.
[sqrt[3]{54}=sqrt[3]{27 * 2}=sqrt[3]{(3 * 3 * 3) * 2}=3 sqrt[3]{2}] в данном случае получившееся подкоренное число 54 можно разложить на произведение двух чисел 27 и 2 , где 27 = 33, тройку выносим за корень кубический, тем самым мы упростили выражение.
Точно также производится умножение корней других степеней, при этом не важно количество умножаемых корней, правило не изменится.
Умножение корней с множителями
В данном случае мы так же рассматриваем примеры умножения корней с одинаковыми степенями. Множителем является число, стоящее перед корнем. Если при написании множитель отсутствует, то он равен единице. Умножить корень на число значит умножить число на множитель перед корнем. Для того чтобы произвести умножение с такими корнями, необходимо перемножить множители.
Пример умножения корней:
[2 sqrt{6} * sqrt{6}=2 sqrt{6 * 6}=2 sqrt{36}=2 * 6=12] в данном примере мы сначала произвели умножение множителей 1 и 2 , затем воспользовавшись первым правилом умножения корней, произвели умножение под знаком корня чисел 6 и 6.
Следующим шагом упрощаем выражение, корень из 36, равен целому числу 6. последним действием умножаем его на полученный множитель 2. и получаем ответ 12.
Пример 2.
[2 sqrt{6} * 3 sqrt{3}=2 * 3 sqrt{6 * 3}=6 sqrt{18}=6 sqrt{9 * 2}=6 * 3 sqrt{2}=18 sqrt{2}]
В приведённом примере, мы также в начале производим умножение множителей 2 и 3, затем производим умножение подкоренных чисел 6 и 3, в результате получаем 6 корней из 18.
После производим упрощение выражения под знаком корня, для этого разложили его на множители, таким образом чтобы одно из чисел можно было вынести за пределы знака корень такими числами стали 9 и 2, в результате получилось, что вынесенное число равно трём, так как 9 = [3^{2}] .
Теперь умножим получившийся ранее множитель 6 на вынесенное из под корня число 3, и получим ответ 18 корней из двух.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Умножение корней с разными показателями
Теперь разберём, как умножить корни если их показатели степени разные. Для этого необходимо найти наименьшее общее кратное число для этих показателей. Таким числом является наименьшее число, которое можно разделить на оба эти показателя. Для того чтобы разобраться лучше в данном методе, приведём пример.
Пример:
[sqrt[2]{2} * sqrt[3]{5}=]
Сначала необходимо найти наименьшее общее кратное, наименьшим в данном случае является произведение 2*3 = 6. Значит для того чтобы произвести умножение корней необходимо привести их к показателю шестой степени.
Записываем новое полученное выражение [sqrt[6]{2} * sqrt[6]{5}=]
Теперь находим числа на которые нужно умножить показатели, чтобы найти наименьшее общее кратное
Для первого корня это деление 62 = 3, для второго 63 =2
Следующим шагом нужно возвести подкоренное число в степень, которая ровна числам найденным ранее, при нахождении НОК, то есть [sqrt[6]{2^{3}} * sqrt[6]{5^{2}}=]
Далее имея одинаковые показатели производим действия по умножению корней, так как делали это в предыдущих правилах.
Если полученное выражение можно упростить, то упрощаем его. В данном случае это невозможно.
Как мы видим произвести умножение корней не так и сложно, главное запомнить основные правила и формулы умножения корней и пользоваться ними.
Как внести под знак корня: число, множитель, букву
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
В данной публикации мы рассмотрим, как число (множитель) или букву внести под знак квадратного и более старших степеней корня. Информация сопровождается практическими примерами для лучшего понимания.
-
Правило внесения под знак корня
- Квадратный корень
- Корень n-ой степени
- Отрицательное число/множитель
- Внесение под корень буквы
Правило внесения под знак корня
Квадратный корень
Чтобы внести число (множитель) под знак квадратного корня, его следует возвести во вторую степень (другими словами, в квадрат), затем полученный результат написать под знаком корня.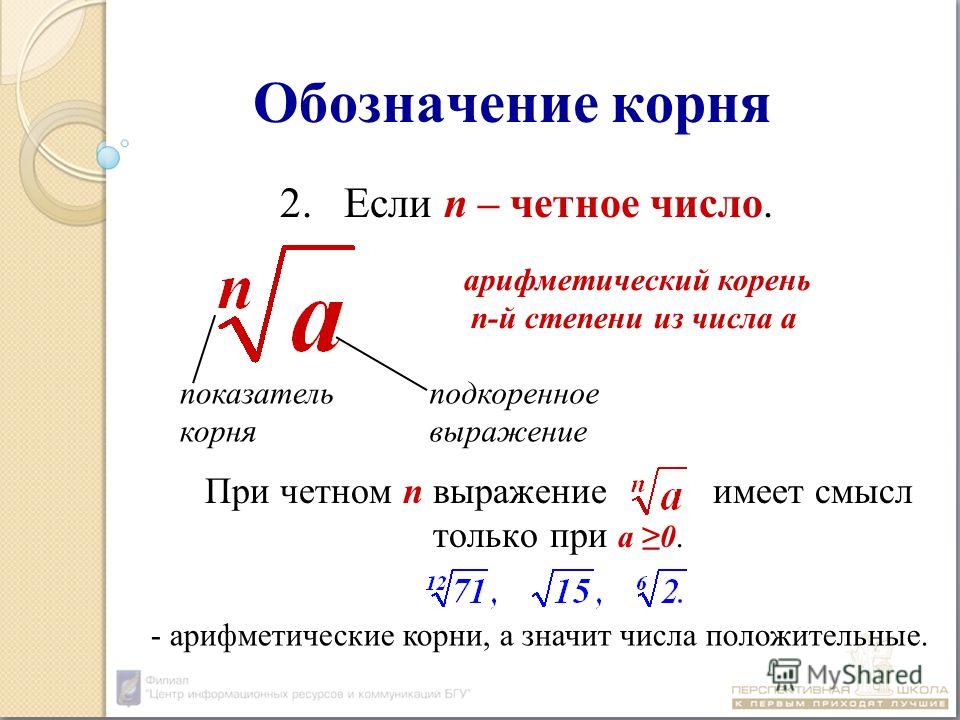
Пример 1: внесем число 7 под квадратный корень.
Решение:
1. Для начала возведем заданное число в квадрат: 72 = 49.
2. Теперь просто записываем рассчитанное число под корнем, т.е. получаем √49.
Коротко внесение под знак корня можно записать так:
Примечание: Если речь идет про множитель, его мы умножаем на уже имеющееся подкоренное выражение.
Пример 2: представим произведение 3√5 полностью под корнем второй степени.
Корень n-ой степени
Чтобы внести число (множитель) под знак кубического и более старших степеней корня, мы возводим это число в заданную ступень, затем переносим результат в подкоренное выражение.
Пример 3: внесем число 6 под кубический корень.
Пример 4: представим произведение 25√3 под корнем 5-ой степени.
Отрицательное число/множитель
При внесении отрицательного числа/множителя под корень (неважно какой степени), знак “минус” обязательно остается перед знаком корня.
Пример 5
Внесение под корень буквы
Чтобы внести букву под знак корня, поступаем так же, как и с числами (в т.ч. с отрицательными) – возводим эту букву в соответствующую степень, после чего добавляем в подкоренное выражение.
Пример 6
Это справедливо при p > 0, если же p – отрицательное число, то перед знаком корня необходимо добавить знак “минус”.
Пример 7
Рассмотрим более сложный случай: (3 + √8) · √5.
Решение:
1. Сперва внесем выражение в скобках под знак корня.
2. Теперь согласно формуле сокращенного умножения возведем выражение (3 + √8) в квадрат.
Примечание: первый и второй шаг можно поменять местами.
3. Остается только выполнить умножение под корнем с раскрытием скобок.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Искусство решения проблем
Корень функции (часто многочлена), диапазоном которой являются действительные, комплексные числа или любое абстрактное поле, является значением в области определения функции таким образом, что .
Содержание
- 1 Поиск корней
- 1.1 Общие методы
- 1.2 Рациональные корни
- 1.3 Действительные корни
- 1.4 Сложные корни
- 1.5 В алгебраической форме
Поиск корней
Пусть при всех и , общая степень-многочлен. Степень , поэтому имеет не более комплексных корней. На самом деле сумма кратностей всех различных комплексных корней точно равна ; то есть, считая любые двойные корни дважды, тройные корни трижды и т. д., на самом деле есть точно комплексные корни .
Общие приемы
Умножение или деление всех коэффициентов многочлена на ненулевую константу не меняет его корней. Таким образом, всегда будет монический полином со степенью, имеющей те же корни, что и , заданный
Как только корень найден, теорема о множителях дает, что это множитель . Следовательно, можно разделить с помощью синтетического деления, а корни полученного частного будут оставшимися корнями из .
Как только будет найден другой корень, процесс можно повторить. Деление на на наиболее практично, когда корень и все коэффициенты рациональны.
Рациональные корни
Три простейших значения для проверки: и .
- является корнем тогда и только тогда, когда постоянный член равен .
- является корнем тогда и только тогда, когда сумма коэффициентов равна .
- является корнем тогда и только тогда, когда сумма переменных коэффициентов равна .
Если все коэффициенты являются целыми числами, то применяется теорема о рациональном корне; а именно, если является корнем , с и относительно простым, то является (положительным или отрицательным) делителем и является делителем .
Если все рациональные, но не обязательно целые числа, то умножение на наименьшее общее кратное знаменателей дает многочлен с теми же корнями, что и целые коэффициенты. Затем к новому многочлену можно применить теорему о рациональном корне для поиска рациональных корней .
В некоторых случаях поиск можно упростить, подставив , где непостоянный линейный полином с рациональными коэффициентами. Если рациональный корень из , то рациональный корень из . Наоборот, если является рациональным корнем , то обратное at должно быть рациональным корнем .
Реальные корни
Вычисление по выбранным значениям может указывать на расположение корней. Если и имеют противоположные знаки, то теорема о промежуточном значении утверждает, что имеет хотя бы один корень в .
Для одинарных корней и других корней нечетной кратности (тройных корней, пятикратных корней и т. д.) всегда будет меняться знак на противоположных сторонах корня, но для корней четной кратности (таких как двойные корни) знак будет быть одинаковым по обе стороны от корня, поэтому теорема о промежуточном значении не обнаружит корни с четной кратностью.
Правило знаков Декарта дает информацию о количестве положительных действительных корней и отрицательных действительных корней .
В более широком смысле, считая корни в соответствии с их кратностью, как и прежде, число действительных корней всегда имеет ту же четность, что и степень . В частности, если нечетно, то должен иметь хотя бы один действительный корень.
Теорема Ролля гарантирует, что если имеет два корня и , то его производная имеет по крайней мере один корень в интервале . В частности, если не имеет корней в отрезке , то имеет не более одного корня в .
Метод Ньютона генерирует сколь угодно близкие приближения значения действительного корня многочлена. Использование метода Ньютона обычно требует обоснованного предположения о местонахождении корня на основе вышеуказанных критериев. Мы позволяем предположению быть равным и вычисляем приближения рекурсивно:
Комплексные корни
Комплексные корни многочленов с вещественными коэффициентами всегда существуют в сопряженных парах. То есть, если , , и все коэффициенты действительны и является корнем, то также является корнем . В частности, должно быть как четное число различных невещественных корней, так и четная сумма кратностей всех различных невещественных корней.
Произведение множителей, соответствующих и, представляет собой квадратичный многочлен с действительными коэффициентами. Таким образом, деление на произведение оставляет многочлен, который все еще имеет действительные коэффициенты и все корни оригинала, кроме и .
В алгебраической форме
Корень многочлена с целыми коэффициентами всегда будет алгебраическим числом.
Для квадратного уравнения корни задаются квадратной формулой
Кубическая формула и формула четвертой степени также существуют, но они довольно длинные и не очень практичны для вычисления вручную.
Для квинтик или многочленов любой более высокой степени не существует подобной формулы. Хотя корнями таких многочленов являются алгебраические числа, их нельзя выразить через коэффициенты, используя только сложение, вычитание, умножение, деление, степени и радикалы.
Эта статья незавершенная. Помогите нам, расширив его.
Краткое руководство по треугольнику 30-60-90
Автор: Мэри Джейн Стерлинг и
-Исчисление для чайников
Исследуйте книгу Купить на Amazon
Треугольник 30-60-90 имеет форму половины равностороннего треугольника, разрезанного прямо посередине вдоль его высоты.
Гипотенуза — самая длинная сторона прямоугольного треугольника, отличная от длинного катета. Длинная нога — это сторона, противоположная углу 60 градусов.
Два самых распространенных прямоугольных треугольника — это 30-60-9.0 и треугольники 45-45-90 градусов. Все треугольники 30-60-90 имеют стороны с одним и тем же основным соотношением. Если вы посмотрите на треугольник с углами 30–60–90 градусов в радианах, это будет выглядеть следующим образом:
На рисунке показано отношение сторон треугольника с углами 30–60–90 градусов.
Прямоугольный треугольник 30-60-90 градусов
Если вы знаете одну сторону треугольника 30-60-90, вы можете найти две другие с помощью ярлыков.
-
Тип 1: Вы знаете короткую ногу (сторона напротив угла 30 градусов). Удвойте его длину, чтобы найти гипотенузу. Вы можете умножить короткую сторону на квадратный корень из 3, чтобы найти длинную сторону.
-
Тип 2: Вы знаете гипотенузу. Разделите гипотенузу на 2, чтобы найти короткую сторону. Умножьте этот ответ на квадратный корень из 3, чтобы найти длинную ногу.
-
Тип 3: Вы знаете длинную сторону (сторона напротив угла 60 градусов). Разделите эту сторону на квадратный корень из 3, чтобы найти короткую сторону. Удвойте это число, чтобы найти гипотенузу.
Нахождение других сторон треугольника 30-60-90, зная гипотенузу
В треугольнике TRI на этом рисунке длина гипотенузы составляет 14 дюймов; как долго другие стороны?
Поскольку у вас есть гипотенуза TR = 14, вы можете разделить на 2, чтобы получить короткую сторону: RI = 7.
Корень из числа
- Квадратный корень
- Арифметический квадратный корень
Корень n-ой степени из числа a — это число, n-ая степень которого равна a. Например, корнем второй степени из 36 будет число 6, так как:
62 = 36.
Для записи корня используется знак √
(знак корня или радикал). Под чертой знака записывается подкоренное число, а над знаком, в левом верхнем углу, показатель корня:
2√36.
Подкоренное число — это степень, показатель корня — это показатель степени, корень — основание степени. Если

то

Эта запись читается так: корень n-ой степени из числа a равен x
.
Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.
Примеры:
3√125 = 5, так как 53 = 125;
2√81 = 9, так как 92 = 81;
5√32 = 2, так как 25 = 32.
Квадратный корень
Квадратным корнем из числа a называется число, квадрат которого равен a.
Например, квадратными корнями из числа 16 являются числа 4 и -4:
2√16 = 4 или 2√16 = -4.
Рассмотрим уравнение
x2 = a
при различных значениях a:
- a < 0:
В данном случае уравнение не будет иметь решений, так как квадрат любого числа всегда является положительным числом или нулём. Следовательно, x2 не может быть равен отрицательному числу.
- a = 0:
В этом случае уравнение имеет единственное решение:
x = 0.
- a > 0:
В этом случае уравнение имеет два корня: положительный и отрицательный, модули которых равны. Так как вторая степень отрицательного числа является числом положительным:
x = ±√a .
Из рассмотренного примера можно сделать вывод, что для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было числом положительным или нулём.
Арифметический квадратный корень
Арифметический квадратный корень из положительного числа a — это положительное число x, квадрат которого равен a:
2√a = x, следовательно x2 = a.
При обозначении квадратного корня показатель корня опускается, то есть квадратный корень обозначается знаком корня без показателя. Например:
√a — квадратный корень из a.
Обратите внимание, что при чтении выражения слово арифметический
опускается.
Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.
Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.
Поэтому для проверки полученного результата можно найденный корень возвести во вторую степень, если степень будет равна подкоренному числу, значит корень был найден правильно.
Рассмотрим извлечение арифметического квадратного корня и его проверку на примере. Найдём √36, для этого надо найти число, при возведении которого во вторую степень получится 36. Таким числом является 6, так как
62 = 36.
Значит, √36 = 6. Корень -6 мы не рассматриваем, потому что арифметический корень является положительным числом.




