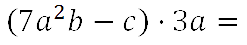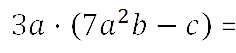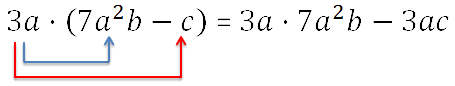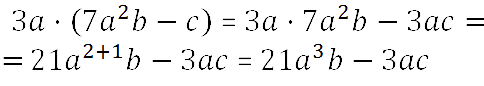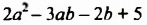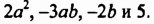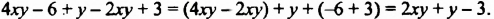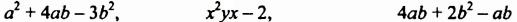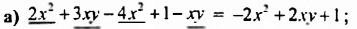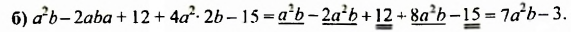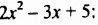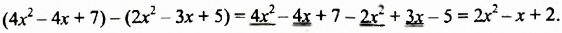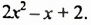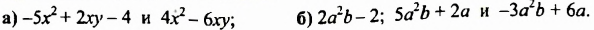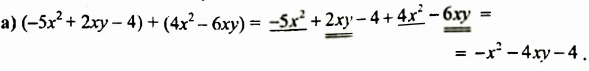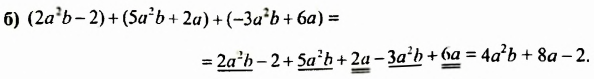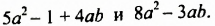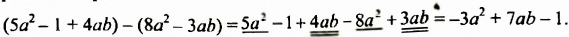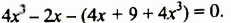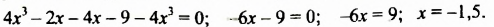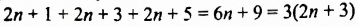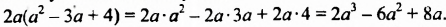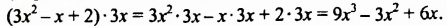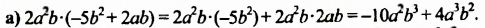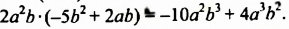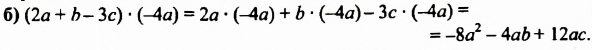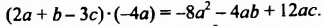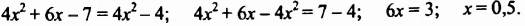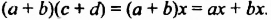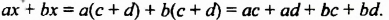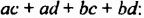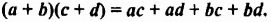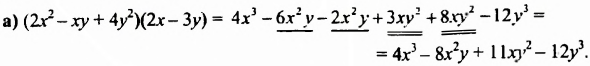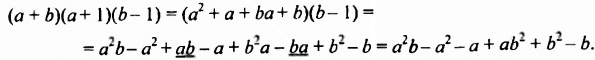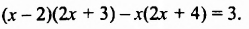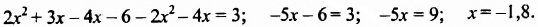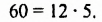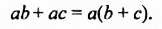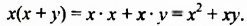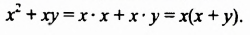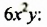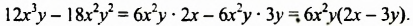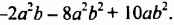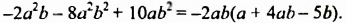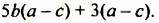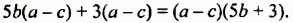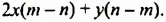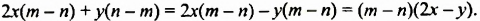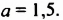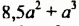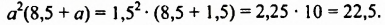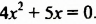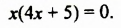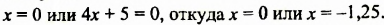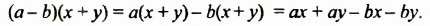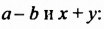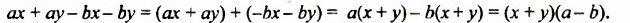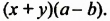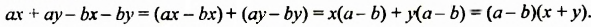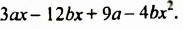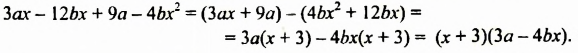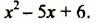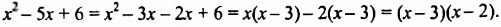Частный случай умножения многочлена на многочлен – умножение многочлена на одночлен. В этой статье сформулируем правило совершения этого действия и разберем теорию на практических примерах.
Правило умножения многочлена на одночлен
Разберемся с тем, что является основой умножения многочлена на одночлен. Данное действие опирается на распределительное свойство умножения относительно сложения. Буквенно это свойство записывается так: (a+b)·c=a·c+b·c (a, b и c – некоторые числа). В этой записи выражение (a+b)·c является как раз произведением многочлена (a+b) на одночлен c. Правая же часть равенства a·c+b·c – это сумма произведений одночленов a и b на одночлен c.
Приведенные рассуждения позволяют нам сформулировать правило умножения многочлена на одночлен:
Для осуществления действия умножения многочлена на одночлен необходимо:
- записать произведение многочлена и одночлена, которые необходимо перемножить;
- умножить каждый член многочлена на заданный одночлен;
- найти сумму полученных произведений.
Дополнительно поясним приведенный алгоритм.
Чтобы составить произведение многочлена на одночлен, исходный многочлен заключают в скобки; далее между ним и заданным одночленом ставится знак умножения. В случае, когда запись одночлена начинается со знака минус, его также необходимо заключить в скобки. К примеру, произведение многочлена −4·x2+x−2 и одночлена 7·y запишем как (−4·x2+x−2)·7·y, а произведение многочлена a5·b−6·a·b и одночлена −3·a2 составим в виде: (a5·b−6·a·b)·(−3·a2).
Следующий шаг алгоритма – перемножение каждого члена многочлена на заданный одночлен. Составляющими многочлена служат одночлены, т.е. по сути нам необходимо выполнить умножение одночлена на одночлен. Допустим, что после первого шага алгоритма мы получили выражение (2·x2+x+3)·5·x, тогда вторым шагом перемножаем каждый член многочлена 2·x2+x+3 с одночленом 5·x, получая таким образом: 2·x2·5·x=10·x3, x·5·x=5·x2 и 3·5·x=15·x. Результатом станут одночлены 10·x3, 5·x2 и 15·x.
Последнее действие согласно правилу – сложение полученных произведений. Из предложенного примера, проделав данный шаг алгоритма, получим: 10·x3+5·x2+15·x.
Стандартно все шаги записывают как цепочку равенств. Например, нахождение произведения многочлена 2·x2+x+3 и одночлена 5·x запишем так: (2·x2+x+3)·5·x=2·x2·5·x+x·5·x+3·5·x=10·x3+5·x2+15·x. Исключив промежуточное вычисление второго шага, краткое решение возможно оформить следующим образом: (2·x2+x+3)·5·x=10·x3+5·x2+15·x.
Рассмотренные примеры дают возможность заметить важный нюанс: в результате перемножения многочлена и одночлена получается многочлен. Данное утверждение верно для любых перемножаемых многочлена и одночлена.
По аналогии осуществляется умножение одночлена на многочлен: заданный одночлен перемножают с каждым членом многочлена и полученные произведения суммируются.
Примеры умножения многочлена на одночлен
Необходимо найти произведение: 1,4·x2-3,5·y·-27·x.
Решение
Первый шаг правила уже выполнен – произведение записано. Теперь выполняем следующий шаг, умножая каждый член многочлена на заданный одночлен. В данном случае удобно сначала перевести десятичные дробив обыкновенные. Тогда получим:
1,4·x2-3,5·y·-27·x=1,4·x2·-27·x-3,5·y·-27·x==-1,4·27·x2·x+3,5·27·x·y=-75·27·x3+75·27·x·y=-25·x3+x·y
Ответ: 1,4·x2-3,5·y·-27·x=-25·x3+x·y.
Уточним, что, когда исходные многочлен и/или одночлен заданы в нестандартном виде, перед тем, как найти их произведение, желательно привести их к стандартному виду.
Заданы многочлен 3+a−2·a2+3·a−2 и одночлен −0,5·a·b·(−2)·a. Необходимо найти их произведение.
Решение
Мы видим, что исходные данные представлены в нестандартном виде, поэтому для удобства дальнейших вычислений приведем их в стандартный вид:
−0,5·a·b·(−2)·a=(−0,5)·(−2)·(a·a)·b=1·a2·b=a2·b3+a−2·a2+3·a−2=(3−2)+(a+3·a)−2·a2=1+4·a−2·a2
Теперь осуществим перемножение одночлена a2·b на каждый член многочлена 1+4·a−2·a2
a2·b·(1+4·a−2·a2)=a2·b·1+a2·b·4·a+a2·b·(−2·a2)==a2·b+4·a3·b−2·a4·b
Мы могли бы не приводить исходные данные к стандартному виду: решение при этом оказалось бы более громоздким. При этом последним шагом возникал бы необходимость приведения подобных членов. Для понимания приведем решение по этой схеме:
−0,5·a·b·(−2)·a·(3+a−2·a2+3·a−2)==−0,5·a·b·(−2)·a·3−0,5·a·b·(−2)·a·a−0,5·a··b·(−2)·a·(−2·a2)−0,5·a·b·(−2)·a·3·a−0,5·a·b·(−2)·a·(−2)==3·a2·b+a3·b−2·a4·b+3·a3·b−2·a2·b=a2·b+4·a3·b−2·a4·b
Ответ: −0,5·a·b·(−2)·a·(3+a−2·a2+3·a−2)=a2·b+4·a3·b−2·a4·b.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Умножение многочлена на одночлен
Поддержать сайт
Запомните!
Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить
на этот одночлен с учетом правила знаков.
Рассмотрим пример умножения многочлена на одночлен.
- Для удобства запишем одночлен перед многочленом, используя
переместительный закон умножения.
- Теперь умножим одночлен на каждый одночлен
в скобках отдельно, не забывая правило знаков.
- Запишем окончательное решение.
Важно!
Будьте внимательны при определении знака результата умножения!
Обязательно помните правило знаков.
Примеры умножения многочлена на одночлен
- 6a(3a − b) = 6a · 3a − 6ab = 18a1 + 1 − 6ab =
18a2 − 6ab
−4a(−a + b) = (−4a) · (−a) − 4ab = 4a · a − 4ab =
4a1 + 1 − 4ab = 4a2 − 4ab
xyz(x2 + 2y2 −3z2) =
xyz · x2 + xyz · 2y2 − xyz · 3z2 =
x2 + 1yz + 2xy2 + 1z −3xyz2 + 1 =
= x3yz + 2xy3z − 3xyz3
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
При умножении одночлена на многочлен используется распределительное свойство умножения:
a(b + c) = ab + ac,
правило умножения степеней с одинаковыми основаниями:
ax · ay = ax + y
и правило знаков при умножении.
Произведением одночлена и многочлена будет многочлен.
Пример 1. Умножить одночлен -5a на многочлен 3a + 4b2.
Решение: Составим произведение одночлена и многочлена и с помощью распределительного свойства умножения раскроем скобки:
Теперь осталось выполнить умножение одночленов друг на друга:
-5a · 3a + (-5a) · 4b2 = -15a2 – 20ab2.
Так как в получившемся результате нет подобных членов, то многочлен -15a2 – 20ab2 — это окончательный результат умножения одночлена -5a на многочлен 3a + 4b2.
Пример 2. Выполните умножение многочлена x – xy + 2 на одночлен 2y.
Решение: Составим произведение многочлена и одночлена:
(x – xy + 2)2y.
Для удобства можно записать одночлен перед многочленом, используя переместительное свойство умножения. После этого раскроем скобки:
Теперь надо перемножить одночлены:
2y · x – 2y · xy + 2y · 2 = 2xy – 2xy2 + 4y.
Решение данного примера можно записать короче, не выписывая промежуточные результаты:
(x – xy + 2)2y = 2xy – 2xy2 + 4y.
Пример 3. Упростите выражение:
3x2 – x(4x – 6y).
Решение: Раскроем скобки, выполнив умножение –x на 4x – 6y, и затем сделаем приведение подобных членов (если они будут):
3x2 – x(4x – 6y) = 3x2 – 4x2 + 6xy = -1x2 + 6xy.
Так как получившийся в результате многочлен является алгебраической суммой, то его можно записать так:
6xy – 1x2.
Логичным началом прохождения новой темы “Многочлены” является вводный урок, освещающий тему умножения многочлена на одночлен. Для начала стоит дать основные определения, которые будут использоваться в этом уроке.
Одночлен – это простое математическое выражение, представляющее собой произведение константы на переменную или несколько переменных, взятых в целой неотрицательной степени без использования знаков + или -.
Многочлен – это сумма одночленов.
Основной задачей этого урока является выведение общего правила умножения одночлена на многочлен, а также развитие навыков для применения этого правила на практике. Обратите внимание, что знания, полученные из этой статьи, пригодятся каждому ученику в течение всего курса изучения алгебры.
Для изучения этой темы вспомним теоретические знания, которые ученики должны получить из предыдущих уроков. Один из необходимых фрагментов теории – свойства степеней.
Задания для тренировки уже имеющихся навыков и проверки знаний
1. Необходимо определить сумму предоставленных одночленов, разность одночленов, произведение одночленов, частное одночленов и квадрат каждого из них.
2. Даны многочлены. Необходимо указать степень каждого из них. Степенью многочлена называется наивысшая степень одночлена, входящего в состав многочлена.
Решив тренировочные упражнения, можно приступить к получению новых знаний.
Правило постановки знаков
1. При умножении двух положительных (+) чисел знак произведения не меняется (+).
2. При умножении двух отрицательных (-) чисел знак произведения меняется на противоположный (+).
3. При умножении положительного (+) числа на отрицательное (-) число произведения отрицательно (-).
Одним словом, ничего сложного.
Умножение одночлена на многочлен
Используем распределительный закон умножения a * (b +c ) =a * b + a * c для решения поставленной задачи:
4x3 (3x2 – 8x + 2) = 3x2 * 4x3 – 8x * 4x3 + 2 * 4x3 = 12х5 – 32х4 + 8х3.
Имея знания по умножению одночлена на одночлен и умножения одночлена на число, вычислим значение данного выражения и сверим получившееся выражение с представленным выше ответом. Важно не забывать и правильно использовать правило постановки знаков.
Умножение многочлена на многочлен
Умножение многочлена на многочлен по своему алгоритму не сильно отличается от умножения одночлена на многочлен. Просто необходимо последовательно перемножить каждый одночлен из одного из многочленов на все одночлены, из которых состоит другой многочлен.
Упражнение для самопроверки:
(5xy −3 x2) * (x2 + 3y) = 5xy * x2 + 5xy * 3y – 3x2 * x2 – 3x2 * 3y = 5x3y + 15xy2 – 3x4 – 9x2y.
Вычислите произведение многочленов самостоятельно и сверьте получившееся выражение с представленным выше ответом. Важно не забывать и правильно использовать правило постановки знаков.
Формулы сокращенного умножения
Усвоив правила умножения, можно и нужно немного расширить свои знания новыми формулами, связанными с данной темой. Важно понимать, что формулы сокращенного умножения по алгебре можно вывести и самостоятельно, пользуясь распределительным свойством умножения, но на практике встречаются они довольно часто, поэтому настоятельно рекомендуется выучить эти формулы.
Необходима проверка. Вы можете самостоятельно умножить многочлен на многочлен и проверить, что после взаимного уничтожения всех вспомогательных слагаемых остаются только указанные в формулах слагаемые.
Геометрический смысл
Для упрощения понимания процесса умножения одночлена на многочлен стоит рассмотреть геометрический смысл этой математической операции.
Здесь важно объяснить обучающимся на примере геометрических фигур распределительный закон умножения и тождественное равенство обеих его частей.
Вопросы для самопроверки
- Что такое одночлен?
- Что такое многочлен?
- Объясните геометрический смысл распределительного закона умножения.
- Опишите алгоритм умножения одночлена на многочлен.
- Какие формулы сокращенного умножения, данные выше, вы запомнили?
Упражнения по пройденной теме
1). -3х3 (х2 + 3х – 4).
2). 15x2 (xy – 4x2y2 + 4).
3). -0,7m3n (10mn – 20m2 – 3).
4). (2a4 – a3 + 0,1a) (-5a2).
5). 0,5с (3с2d – 15c3d).
6). 0,5p2 (4q – 2pq + 6p2).
7). 20xy2 (5x2y – 2,4y – 0,6).
8). 4a2b (2a – 3ab2 + 8b2).
Тест: умножение многочлена на одночлен
Для проверки полученных знаний ниже предлагается специальный тест.
| 1. Узнайте произведение: -5х (-3х + 2х2 – 2).
а) -10х3 – 15х2 + 10х. б) -10х3 + 15х2 – 10х. в) -10х3 – 15х2 + 10. г) -10х3 + 15х2 + 10х |
| 2. Замените знак (*) на выражение для получения истинного равенства:
-2х2 (*) = -8х4а2 + 4х2а – 6х4. а) 4а2х – 2а – 3х2. б) 3х2 – 2а + 4а2х2. в) 2а – 3х2 – 4а2х2. г) -4а2х2 + 3х2 + 2а |
|
3. Найдите произведение: 3а (2в – а) – 4в (в + 2а). а) 3а2 – 4b2. б) -3а2 – 2ab – 4b2. в) 3а2 + 2ab + 4b2. г) -3а2 – 4b2 |
| 4. Найдите корень заданного уравнения: 8х2 + 3х = 0.
а) х = 0. б) х = -(3/8). в) х = 0; х = (3/8). г) х = 0; х = -(3/8) |
| 5. Определите делитель данного выражения: 54 + 55 + 56.
а) 15. б) 31. в) 10. г) 55 |
Ключи к тесту: 1-г; 2-б; 3-б; 4-г; 5-б.
Заключение
На этом уроке обучающиеся получили теоретический материал с практическими примерами его применения по теме “Умножение одночлена на многочлен”. А также узнали дополнительный материал, который пригодится им в дальнейшем изучении предмета. А именно, формулы сокращенного умножения по алгебре.
В процессе выполнения упражнений развивалось аналитическое мышление у обучающихся.
Обучающимися должны были быть сделаны определенные выводы о применении этой темы на практике. Умножение одночлена на многочлен применяется:
- в процессе упрощения выражений;
- в процессе нахождения корня уравнения;
- с целью доказательства некоторых тождественных выражений;
- в процессе решения задач на составление уравнений.
Содержание:
Многочлены
Многочлен
Выражение
Определение: Многочленом называют сумму нескольких одночленов.
Одночлены, составляющие многочлен, называют членами этого многочлена.
Например, членами многочлена 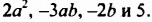
Многочлен, состоящий из двух членов, называют двучленом, многочлен, состоящий из трех членов, — трехчленом и т. д. Так,
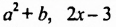
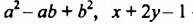
Считают, что каждый одночлен является многочленом, который состоит из одного члена.
Многочлен стандартного вида
Рассмотрим многочлен 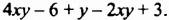
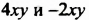
Приведем в многочлене 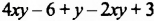
Многочлен 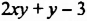
Определение:
Многочлен, являющийся суммой одночленов стандартного вида, среди которых нет подобных членов, называют многочленом стандартного вида.
Среди многочленов
только первый является многочленом стандартного вида, а два другие — нет, поскольку во втором многочлене первый член не является одночленом стандартного вида, а третий многочлен имеет подобные члены.
Степень многочлена
Многочлен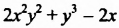
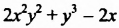
Определение:
Степенью многочлена стандартного вида называют наибольшую степень одночленов, образующих данный многочлен.
По этому определению 
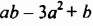
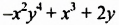
Члены многочлена можно записывать в произвольном порядке. Для многочленов стандартного вида, содержащих одну переменную, члены, как правило, записывают в порядке убывания или возрастания показателей степеней. Например:
Каждый многочлен является целым выражением. Однако не каждое целое выражение является многочленом. Например, целые выражения 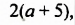
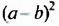
Примеры выполнения заданий:
Пример №117
Записать в стандартному виде многочлен:
Сложение и вычитание многочленов
Сложение многочленов
Сложим многочлены
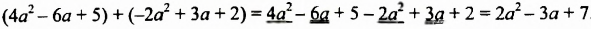
Раскрыв скобки и приведя подобные слагаемые, мы записали сумму данных многочленов в виде многочлена. Итак, суммой многочленов 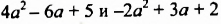
Таким же образом находят сумму трех и более многочленов. Сумму любых многочленов всегда можно записать в виде многочлена.
Вычитание многочленов
Вычтем из многочлена 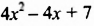
Раскрыв скобки и приведя подобные слагаемые, мы записали разность данных многочленов в виде многочлена. Итак, разностью многочленов 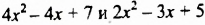
Разность любых многочленов всегда можно записать в виде многочлена.
Примеры выполнения заданий:
Пример №118
Найти сумму многочленов:
Пример №119
Найти разность многочленов
Решение:
Пример №120
Решить уравнение
Решение:
Ответ.-1,5.
Пример №121
Доказать, что сумма трех последовательных нечетных чисел делится на 3.
Решение:
Пусть из трех последовательных нечетных чисел наименьшим является 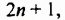
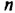
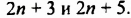
делится на 3, поскольку имеет делитель 3.
Умножение одночлена на многочлен
Умножим одночлен 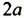
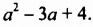
Итак, произведением одночлена 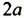
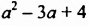
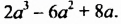
Чтобы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена и полученные произведения сложить.
По этому правилу можно умножать и многочлен на одночлен. Например:
Произведение любого одночлена и любого многочлена всегда можно :ать в виде многочлена.
Примеры выполнения заданий:
Пример №122
Выполнить умножение:
Сокращенная запись:
Сокращенная запись:
Пример №123
Упростить выражение
Решение:
Пример №124
Решить уравнение
Решение:
Ответ. 0,5.
Умножение многочлена на многочлен
Умножим многочлен 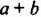
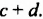
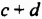
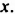
Возвращаясь к замене 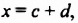
Итак, произведением многочлена 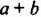
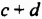
Выражение 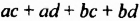
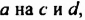
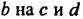
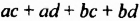
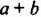
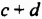
Приходим к такому правилу:
Чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Умножим по этому правилу многочлен 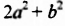
Выполняя умножение многочленов, промежуточные результаты можно не записывать:
В каждом из рассмотренных примеров произведение двух многочленов мы записывали в виде многочлена. Вообще, произведение любых многочленов всегда можно записать в виде многочлена.
- Заказать решение задач по высшей математике
Примеры выполнения заданий:
Пример №125
Выполнить умножение:
б) Найдем произведение первых двух многочленов, а потом полученное произведение умножим на третий многочлен:
Пример №126
Решить уравнение
Решение:
Ответ.-1,8.
Разложение многочленов на множители способом вынесения общего множителя за скобки
1. В шестом классе мы изучали разложение чисел на множители. Например, число 60 можно записать в виде произведения двух чисел 12 и 5:
Говорят, что число 60 разложили на два множителя 12 и 5.
На множители можно разложить и многочлены. Например,
Записав многочлен 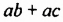
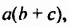
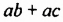
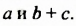
Разложить многочлен на множители значит представить его в виде произведения нескольких многочленов.
Сравните
2. Рассмотрим один из способов разложения многочленов на множители. Выполним умножение одночлена на многочлен:
Перепишем эти равенства в обратном порядке:
Многочлен 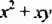
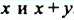
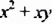
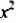
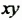
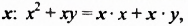
Такой способ разложения многочленов на множители называют способом вынесения общего множителя за скобки.
Примеры выполнения заданий:
Пример №127
Разложить на множителя многочлен 12х3у – 18х2у2.
Решение:
Сначала найдем общий числовой множитель для коэффициентов 12 и -18. Если коэффициентами являются целые числа, то в качестве общего числового множителя берут, как правило, наибольший общий делитель модулей этих коэффициентов. В нашем случае это число 6. Степени с основанием 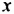
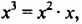
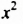
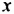
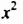
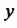
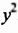
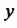
Пример №128
Разложить на множители многочлен
Решение:
Пример №129
Разложить на множители:
Решение:
Данное выражение является суммой двух слагаемых, для которых общим множителем является выражение 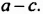
Пример №130
Разложить на множители:
Решение:
Слагаемые имеют множители 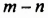
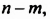
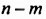
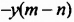
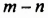
Следовательно,
Пример №131
Найти значение выражения 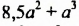
Решение:
Разложим сначала многочлен 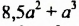
При 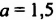
Пример №132
Решить уравнение
Решение:
Разложим левую часть уравнения на множители:
Произведение 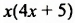
Ответ. 0; -1,25.
Разложение многочленов на множители способом группировки
Изучение этого способа разложения многочленов на множители начнем с рассмотрения примера умножения многочленов. Выполним умножение двучлена 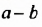
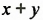
Выполняя преобразования в обратном порядке, многочлен 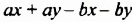
Проанализируем последние преобразования. Имеем многочлен, члены которого можно группировать так, чтобы каждая группа имела общий множитель: для группы 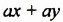
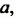
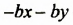
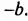
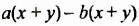
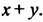
Рассмотренный способ разложения многочленов на множители называют способом группировки. При применении этого способа нужно образовывать такие группы членов, чтобы они имели общий множитель. После вынесения в каждой группе общего множителя за скобки должен образоваться общин множитель для всех групп, который также нужно вынести за скобки.
Многочлен 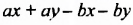
Сравните
Примеры выполнения заданий:
Пример №133
Разложить на множители многочлен
Решение:
Пример №134
Разложить на множители трехчлен
Решение:
Представим второй член 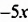
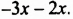
- Формулы сокращенного умножения
- Разложение многочленов на множители
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены