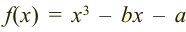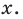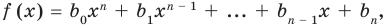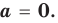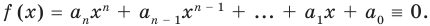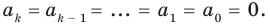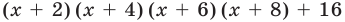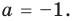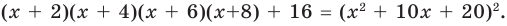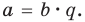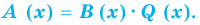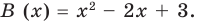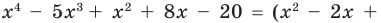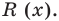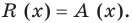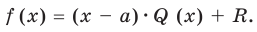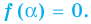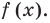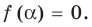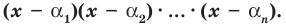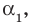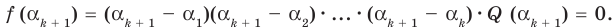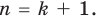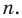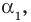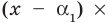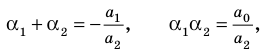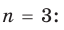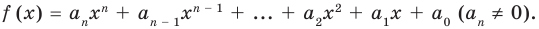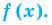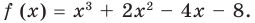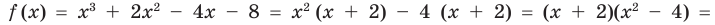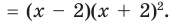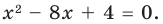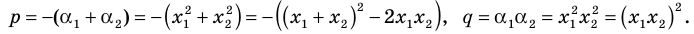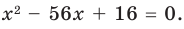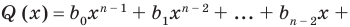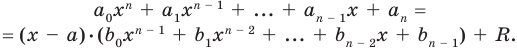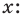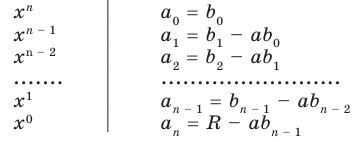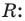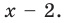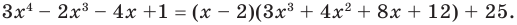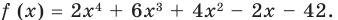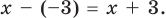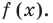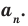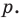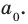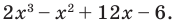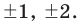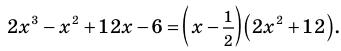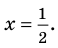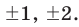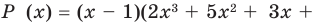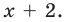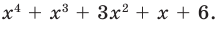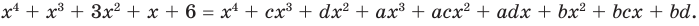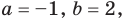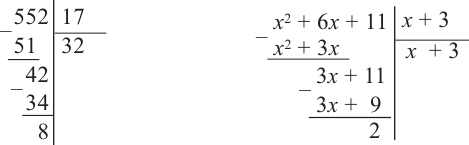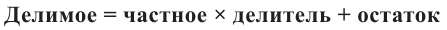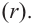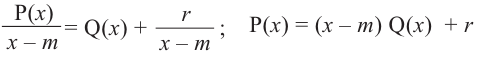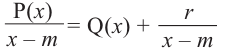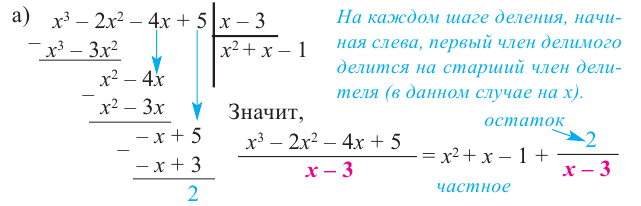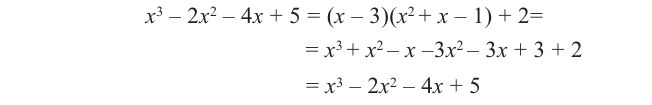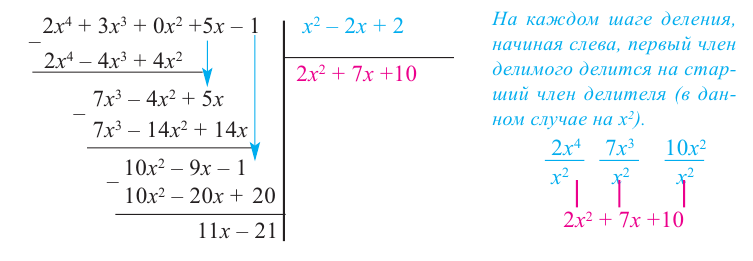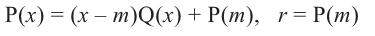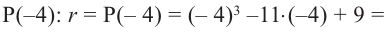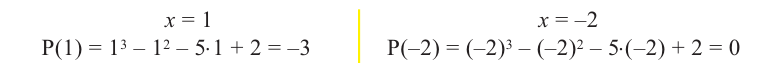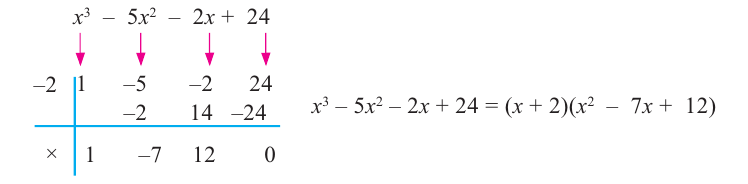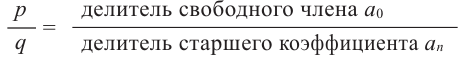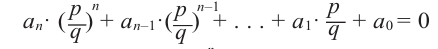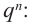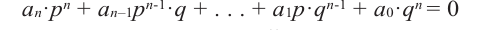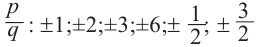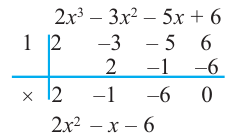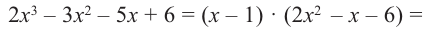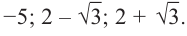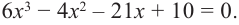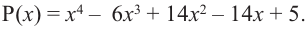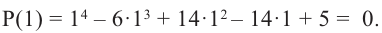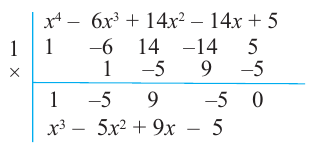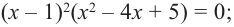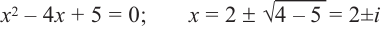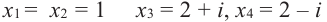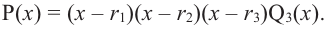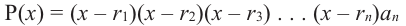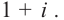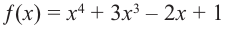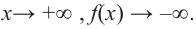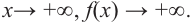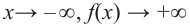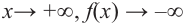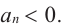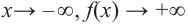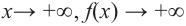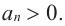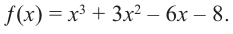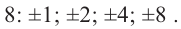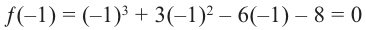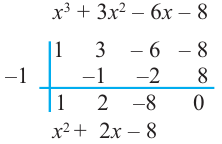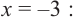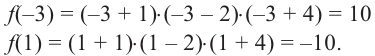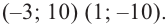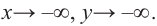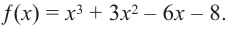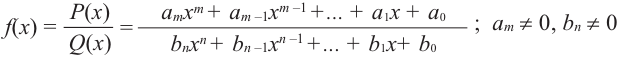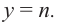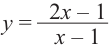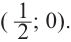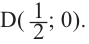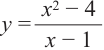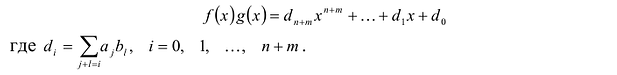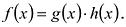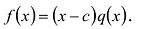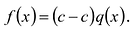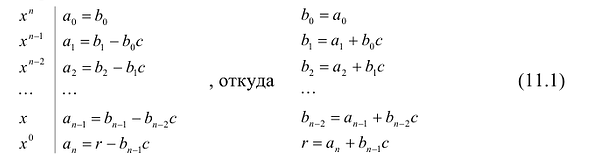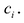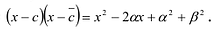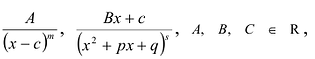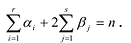Часто путают понятия одночлена и многочлена.
Давайте разберемся, что называют одночленом, а что многочленом.
Прежде всего, вспомним, что называли одночленом в уроке «Одночлены».
Обратите внимание, что «внутри» одночлена (между буквами и числовым коэффициентом) есть только знак умножения.
Например, в одночлене:
3ab = 3 · a · b
Запомните!
Многочленом называется алгебраическая сумма нескольких одночленов.
Одночлены, из которых составлен многочлен, называют членами многочлена.
Примеры многочленов:
a + 2b2 − c;
3t5 − 4b;
4 − 6xy
Несложно заметить, что любой многочлен состоит из нескольких одночленов.
Рассмотрим многочлен подробнее.
Возникает вопрос, почему многочленом называют алгебраическую сумму
одночленов, если в многочлене присутствует
знак минуса.
Это объясняется тем, что на самом деле знак «−» относится к числовому коэффициенту одночлена,
который стоит справа от знака.
Любой многочлен можно записать
по правилу знаков
как сумму одночленов.
В многочлене знак, который стоит слева от одночлена относится к числовому коэффициенту самого одночлена.
Как найти степень многочлена
Запомните!
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
То есть, чтобы найти степень многочлена, нужно сначала найти
степень каждого одночлена, который входит в
состав многочлена.
Степени многочленов
| Многочлен |
Степень многочлена |
||||
|---|---|---|---|---|---|
|
a2 − 3a2b + x = a2(степень одночлена 2) |
3 | ||||
x2y2
x2y2(степень одночлена 4) |
4 | ||||
|
8x2 8x2(степень одночлена 2) |
2 |
Любой одночлен является многочленом.
В самом деле, любой одночлен, по сути, является многочленом, который состоит всего из одного одночлена.
Примеры таких многочленов: 2a2b;
−3d3; a.
Число «0» называют нулевым многочленом.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
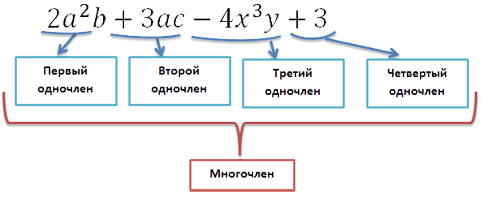
Многочлен – это сумма одночленов. Одночлены, которые составляют многочлен, называют членами данного многочлена. Если многочлены состоят из двух или трех слагаемых, то их можно называть двучленами или трехчленами соответственно.
Пример №1.
- –12х6+ 35с данный многочлен состоит из двух слагаемых – одночленов, таких как: –12х6 и 35с. Еще такой многочлен можно называть двучленом.
- 47с2+11с–34 данный многочлен состоит из трех слагаемых. Такой многочлен можно назвать трехчленом.
- 4х3+13а2–45с+28 данный многочлен состоит из четырех слагаемых – одночленов, таких как: 4х3; 13а2; – 45с; 28.
Стандартный вид многочлена
Что такое стандартный вид многочлена?
Многочлен называется приведенным к стандартному виду, если он не имеет подобных слагаемых, и каждый его член имеет также стандартный вид.
Вспомним, что слагаемые, содержащие одинаковую буквенную часть или не имеющие буквенной части называют подобными. Если такие слагаемые есть, то их нужно сложить или вычесть, это действие называют приведением подобных слагаемых.
Пример №2.
13х2–6х+11х2
Данный трехчлен имеет подобные слагаемые (они выделены). Они имеют одинаковые знаки, поэтому мы их складываем и получаем 24х2. Слагаемое –6х не имеет подобных, поэтому его просто переписываем и получаем многочлен в стандартном виде:
13х2–6х+11х2=24х2–6х
Пример №3.
6а3с4+32х–9а3с4+45х–16
Данный многочлен имеет две группы подобных слагаемых, одна выделена красным цветом, вторая синим цветом, слагаемое –16 не имеет подобных, поэтому его просто перепишем. Приводим подобные слагаемые и получаем многочлен стандартного вида:
6а3с4+32х–9а3с4+45х–16= –3а3с4+77х–16
Степень многочлена
Что такое степень многочлена?
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. При этом многочлен должен быть записан в стандартном виде. Рассмотрим на примерах, как определить степени многочленов.
Пример №4.
4с6+7а9–18х
Степень многочлена, записанного в стандартном виде, равна 9, так как одночлен 7а9 имеет степень равную 9 и она наибольшая по сравнению со степенями одночленов 4с6 и –18х.
Пример №5.
13х4у7+12х3у6–13
степень данного многочлена стандартного вида находим по наибольшей степени каждого одночлена: одночлен 13х4у7 имеет 11 степень, так как складываем показатели 4 и 7; одночлен 12х3у6 имеет соответственно 9 степень, а –13 имеет степень равную нулю (не содержит переменных). Таким образом, получается, что наибольшая степень равна 11, значит и степень всего многочлена равна 11.
Пример №6.
6а5+8ас+2а5–11ас
Данный многочлен не является многочленом стандартного вида, поэтому сначала приведем подобные слагаемые, получим 6а5+8ас+2а5–11ас=8а5–3ас. Теперь найдем степень у каждого одночлена: у 8а5 пятая степень, у 3ас – вторая (каждая переменная имеет первую степень). Значит, у многочлена 6а5+8ас+2а5–11ас степень равна 5.
Сложение и вычитание многочленов
Многочлены можно как складывать, так и вычитать. То есть сумму или разность многочленов можно представить в виде многочлена стандартного вида. Рассмотрим на примерах сложение и вычитание многочленов.
Пример №7. Выполним сложение многочленов:
6х2+8х–11 и –9х2+3х+19
Сначала составим их сумму (6х2+8х–11) + (–9х2+3х+19), теперь раскроем скобки, помня о том, что, если перед скобками стоит знак «плюс», то знаки у слагаемых в скобках не изменяются:
6х2+8х–11–9х2+3х+19
Теперь приведем подобные слагаемые и получим многочлен стандартного вида:
–3х2+11х+8
Пример №8. Выполним вычитание многочленов:
7х5+12х3–24 и 2х5+36х3–11
Составим разность многочленов (7х5+12х3– 24) – (2х5+36х3–11), раскроем скобки, помня о том, что, если перед скобками стоит «минус», то надо изменить знаки у слагаемых в скобках на противоположные:
7х5+12х3– 24 – 2х5–36х3+11
Приведем подобные слагаемые и получим многочлен:
5х5– 24х3–13
Умножение одночлена на многочлен
Как умножить многочлен на одночлен?
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена.
Пример №9. Умножим одночлен 7х на многочлен 6х2+3х–5. Запишем в виде произведения:
7х•(6х2+3х–5)
выполним умножение 7х на каждое слагаемое в скобках: 7х•6х2+7х•3х–7х•(–5) и получим:
42х3+21х2+35х
Запись данного выражения можно делать короче, выполняя промежуточные действия устно:
7х•(6х2+3х–5)= 42х3+21х2+35х
Пример №10.
92с(–2с+10а6)= –184с2+920са6
Здесь выполнение умножения одночлена на многочлен выполнено без записи промежуточных действий умножения.
Умножение многочлена на многочлен
Как умножить многочлен на многочлен?
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Пример №11. Умножим многочлен (а+с) на многочлен (х+с).
Составим произведение (а+с)(х+с); умножим сначала а на (х+с), затем с на (х+с); получим:
ах+ас+сх+с2
Получили многочлен в стандартном виде. Здесь были даны простые многочлены, не содержащие степеней. Запись выражения выглядит так:
(а+с)(х+с)=ах+ас+сх+с2
Пример №12. Умножим многочлен 8х3–12х на многочлен 3х5–10х. Имеем:
(8х3–12х)(3х5–10х)=8х3•3х5+8х3•(–10х)–12х•3х5–12х•(–10х)=24х8–80х4 –36х6+120х2
Здесь были даны многочлены, содержащие степень, поэтому промежуточное решение лучше расписывать, чтобы не допустить ошибок.
Разложение многочлена на множители
Существуют такие способы для разложения многочлена на множители, как вынесение общего множителя за скобки и разложение на множители способом группировки.
Способ №1. Вынесение общего множителя за скобки.
Вынесение общего множителя за скобки – это представление многочлена в виде произведения одночлена и многочлена.
Пример №13. Вынесем общий множитель в выражении 6х4 – 20х2. Для этого удобнее сначала найти наибольший общий делитель у чисел – это число 2, а затем общий делитель у переменных, которые одинаковы по своей буквенной части, но имеют разные показатели степени. В этом случае общим делителем является переменная в наименьшей степени, то есть х2. Запись выглядит следующим образом:
6х4 – 20х2=2х2(3х2–10)
При вынесении за скобки степеней помним правило, что при делении степеней с одинаковым основанием показатели вычитаем, а основание оставляем прежним.
Пример №14. Разложим на множители многочлен:
12с5х7–36с6х2+72асх3
Найдем сначала наибольший делитель для чисел 12, 36 и 72, это будет 12. Затем выберем у переменных те, которые имеют наименьшую степень и содержатся в каждом слагаемом, это с и х2. Вынесем за скобки 12сх2 и получим:
12с5х7–36с6х2+72асх3=12сх2(с4х5–3с5+6ах)
Сделаем вывод, что вынесение общего множителя за скобки – это выполнение действия деления каждого члена многочлена на его общий делитель.
Способ №2. Способ группировки.
Чтобы выполнить разложение на множители способом группировки необходимо следовать определенному алгоритму (ключевое слово в данном способе – группировка). Группировка слагаемых выполняется таким образом, чтобы в каждой группе можно было выполнить вынесение общего множителя за скобки, а в скобках оставались одинаковые выражения, это обычно определяется устно.
Пример №15. Разложим на множители многочлен:
ах+сd+cx+ad
Сгруппируем, например, слагаемые первое с последним, а второе с третьим (можно было первое с третьим, а второе с последним):
(ах+ad)+(сd+cx)
Теперь видим, что в каждой группе есть множитель, который можно вынести за скобки:
(ах+ad)+(сd+cx)= а(х+d)+с(d+x)
В полученном выражении видно, что в обеих скобках есть сумма х и d, вынесем эту сумму снова за скобки:
(ах+ad)+(сd+cx)= а(х+d)+с(d+x)= (х+d)(с+а)
Таким образом, мы получили произведение двух выражений, то есть разложили данный многочлен на множители.
Пример №16. Разложим на множители многочлен:
7a–7b+an–bn
Сгруппируем по порядку, чтобы знаки у слагаемых в скобках были одинаковые:
7a–7b+an–bn=(7a–7b)+(an–bn)
Вынесем общий множитель в каждой группе:
7a–7b+an–bn=(7a–7b)+(an–bn) =7(a–b)+n(a–b)
Вынесем за скобки одинаковые выражения:
7a–7b+an–bn=(7a–7b)+(an–bn) =7(a–b)+n(a–b)=(a–b)(7+n)
Пример №17. Разложим на множители многочлен:
х5–х3–х2+1
Сгруппируем по порядку, обращая внимание на знак перед х2:
х5–х3–х2+1 =(х5–х3)–(х2–1)
Если перед первым слагаемым, которое мы заключаем в скобки, стоит знак «минус», то мы ставим его перед скобкой, а знаки у слагаемых в скобках изменяем на противоположные. Тогда у нас в обеих скобках получатся одинаковые знаки.
Выносим за скобки общий множитель. В данном случае он есть только в первых скобках:
х5–х3–х2+1 =(х5–х3)–(х2–1)= х3(х2–1)–(х2–1)
Выносим за скобки одинаковые выражения, обращая внимание на то, что перед второй скобкой не записан общий множитель, значит, он равен 1:
х5–х3–х2+1 =(х5–х3)–(х2–1)= х3(х2–1)–(х2–1)=(х2–1)(х3–1)
Алла Василевская | Просмотров: 4.7k
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 ноября 2022 года; проверки требуют 2 правки.
Степенью многочлена одной комплексной переменной называется количество всех его корней с учётом их кратности. Из основной теоремы алгебры и из следствия теоремы Безу следует, что любой многочлен p(x) степени n возможно представить в виде a(x − x1)…(x − xn), где x1, …, xn — это все комплексные корни многочлена с учётом кратности, а константа a ≠ 0 — старший коэффициент многочлена. Раскрыв скобки в выражении a(x − x1)…(x − xn), можно получить эквивалентное определение: степень многочлена одной переменной — это максимальная из степеней всех его слагаемых-одночленов, тождественно не равных нулю.
Это определение имеет обобщение: полная степень многочлена с несколькими переменными — это максимальная из степеней всех его одночленов, тождественно не равных нулю, относительно всех переменных, участвующих в них, одновременно.
Многочленное уравнение d переменных, которое с помощью равносильных преобразований можно привести к виду p(x1,…,xd) = 0, где полином p(x1, …, xd) имеет степень n, называется (многочленным) уравнением степени n.
Степень полинома обозначается deg (англ. degree, фр. degré, от лат. gradus + de-).[1]
Названия определённых степеней[править | править код]
- Степень многочлена, тождественно равного нулю, не определена, но в некоторых случаях её принимают равной −1 или −∞ (ниже).[2]
- Степень константы, не равной нулю, — 0.
- Степень линейного многочлена — 1. Уравнение, в котором линейная функция приравнивается нулю, — уравнение 1-й степени.
- Степень квадратного многочлена — 2. Соответствующее уравнение — уравнение 2-й степени.
- Степень кубического многочлена — 3. Ему соответствует уравнение 3-й степени.
В d-мерном евклидовом пространстве (d − 1)-мерная поверхность, являющаяся решением уравнения p(x1,…,xd) = 0 степени n с декартовыми координатами x1, …, xd, называется (d − 1)-мерной поверхностью n-го порядка. Термин порядок фактически означает степень уравнения. Отдельные названия гиперповерхностей:
- квадрика — гиперповерхность второго порядка. В одномерном случае квадрика представляет собой конику — плоскую кривую, один из эквивалентных способов получить которую — пересечь прямой круговой конус плоскостью;
- кубика — гиперповерхность третьего порядка. Примеры плоских кубик: кубика Чирнгауза, полукубическая парабола;
- квартика — гиперповерхность 4-го порядка: например, квартика Люрота.
Примеры[править | править код]
- Многочлен x(x − 2) имеет вторую степень, так как он состоит из двух линейных сомножителей.
- У многочлена (2x − 1)(3x − 2) коэффициенты 2 и 3 можно вынести за скобки: 2 × 3(x − 12)(x − 23), — так что он имеет степень 2.
- У многочлена 16x5 + (−20)x3 + 5x + (−1) одночлен с наибольшей степенью — это 16x5, а значит, степень многочлена равна 5.
- Многочлены могут быть записаны в неканоническом виде: например, полином (x2 + 1)2 − (−x2 + 1)2 имеет степень 2, так как он представляет собой одночлен 4x2.
- Многочлен 2(2x − y)xy является третьей степени.
- Многочлен x2 + y имеет вторую степень, поскольку одночлен с наибольшей степенью равен x2, причём этот многочлен уже нельзя разложить на линейные множители от x и y.
- Степень многочлена xy + y + x равна 2.
Степень многочлена при операциях над ними[править | править код]
Умножение[править | править код]
При умножении ненулевого многочлена p(x) на ненулевую константу c степень не изменяется:
Например, степень полинома 6(x − 12)(x − 23) = 6x2 − 5x + 2, как и (x − 12)(x − 23) = x2 + −56x + 13, равна 2. В более общем случае степень произведения полиномов p(x) и q(x) равна сумме степеней этих полиномов:[3][4]
К примеру, степень многочлена (x2 + 1)(x3 − x − 1) = x5 − x2 − x − 1 равна 2 + 3 = 5.
Сложение, вычитание[править | править код]
Степень суммы ненулевых многочленов не может быть больше максимальной из их степеней:[5][6]
То же самое неравенство верно и для разности:
При этом если степени многочленов-слагаемых различаются, то вышенаписанные соотношения обращаются в равенства. Например, многочлен (x2 + 1)2 имеет четвёртую степень, (x + 1)2 — вторую, а многочлены (x2 + 1)2 ± (x + 1)2 — 4-ю.
Композиция[править | править код]
Пусть p(x) и q(x) — ненулевые многочлены. Тогда:[7]
Например, если p(x) = x2 + 1, q(x) = x3 + 1, то степени многочленов p ∘ q(x) = x6 + 2x3 + 2 и q ∘ p(x) = x6 + 3x4 + 3x2 + 2 равны 2 × 3 = 6.
Степень многочлена нескольких переменных[править | править код]
Как и в случае с одной переменной, (полная) степень одночлена нескольких переменных — сумма всех показателей степеней всех переменных в одночлене. К примеру, полная степень одночлена x1y2x3 относительно x и y равна 1 + 2 + 3 = 6.
В свою очередь, (полная) степень многочлена нескольких переменных — это максимальная из степеней всех его одночленов. Пример: многочлен xy + y + x имеет степень 2, так как одночлен с наибольшей степенью — xy.
Помимо этого, степень многочлена нескольких переменных может также рассматриваться относительно одной из переменных. Например, полином x2 + y2 + xy + x + y имеет 2-ю степень относительно x и ту же степень относительно y. Причём относительно x этот полином раскладывается на комплексные линейные множители так:
а относительно y:
Иногда на степень полинома относительно конкретной переменной могут влиять другие переменные: например, полином (x2 + 1)y2 + (x + 1)y + 1 четвёртой степени является квадратным относительно y, только если x не равняется ±i, — в противном случае одночлен (x2 + 1)y2 обратится в нуль и многочлен станет линейным: его нельзя будет разложить на два линейных множителя (относительно y).
Степень нулевого многочлена[править | править код]
Степень многочлена, равного 0 при любом значении переменной(-ых), считается либо неопределённой[8], либо отрицательной — как правило, −1[9] или −∞.[2][10]
В случае, когда степень такого многочлена не определена, полагают, что нулевой многочлен, строго говоря, вообще не имеет никаких одночленов-слагаемых, которые тождественно не равнялись бы нулю. Соответственно, для нулевого многочлена совсем не вводятся никакие вышенаписанные свойства степеней при преобразовании многочленов.
При этом в случае, когда степень нулевого полинома принимают равной −∞, сохраняются все свойства, приведённые выше, исключая, быть может, композицию. Для любого вещественного числа n по определению выполняются следующие свойства (свойства аффинно расширенной числовой прямой):
Соответственно, сами степени многочленов «ведут себя» следующим образом: если p(x) — ненулевой многочлен степени n, то
Примечания[править | править код]
- ↑ Eric W. Weisstein. Polynomial Degree (англ.). mathworld.wolfram.com. Дата обращения: 28 мая 2021. Архивировано 3 июня 2021 года.
- ↑ 1 2 Eric W. Weisstein. Zero Polynomial (англ.). mathworld.wolfram.com. Дата обращения: 28 мая 2021. Архивировано 1 мая 2021 года.
- ↑ Serge Lang. Algebra. — 3. — New York: Springer-Verlag, 2002. — (Graduate Texts in Mathematics). — ISBN 978-0-387-95385-4.
- ↑ Серж Ленг. Алгебра. — Springer, 2005. — С. 100. — ISBN 978-0-387-95385-4.
- ↑ abstract algebra – The degree of a sum of two polynomials (proof question). Mathematics Stack Exchange. Дата обращения: 28 мая 2021.
- ↑ Degree of sum of polynomials – TheoremDep. sharmaeklavya2.github.io. Дата обращения: 28 мая 2021. Архивировано 20 января 2021 года.
- ↑ algebra precalculus – What’s polynomial composition useful for? Mathematics Stack Exchange. Дата обращения: 28 мая 2021.
- ↑ Шафаревич, Игорь Ростиславович. Лекции по алгебре. — С. 25. Архивная копия от 2 июня 2021 на Wayback Machine
- ↑ Чайлдс, Линдсей. Конкретное введение в высшую алгебру. — 1995. — С. 233. Архивная копия от 2 июня 2021 на Wayback Machine
- ↑ 1 2 Чайлдс, Линдсей. Конкретное введение в высшую алгебру.. — 2009. Архивная копия от 2 июня 2021 на Wayback Machine
Ссылки[править | править код]
- https://mathworld.wolfram.com/PolynomialDegree.html
- https://www.mathsisfun.com/algebra/degree-expression.html
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 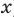
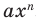
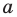
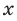
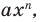
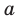
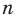
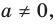
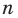
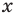
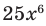
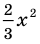
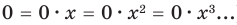
По определению многочлен от одной переменной 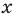
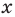
многочленом от одной переменной 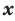
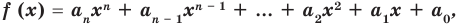
где коэффициенты 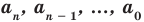
Если 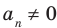
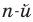
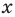
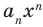
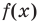
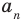
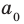
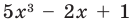
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 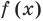
где 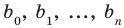
Теорема 1. Одночлены 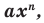
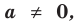
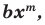
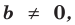
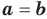
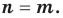
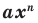
Поскольку равенство одночленов
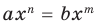
выполняется при всех значениях 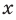
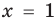
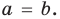
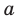
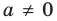
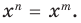
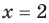
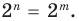
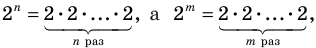
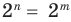
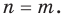
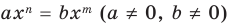
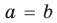
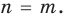
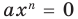
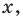
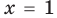
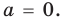
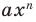
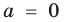
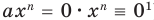
Далее любой одночлен вида 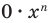
Теорема 2. Если многочлен 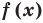
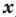
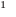
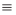
Для доказательства используем метод математической индукции. Пусть
При 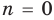
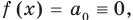
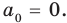
Предположим, что при 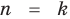
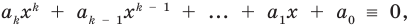
Докажем, что данное утверждение выполняется и при 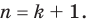
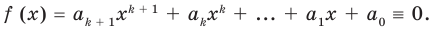
Поскольку равенство (3) выполняется при всех значениях 
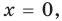
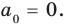
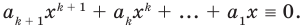

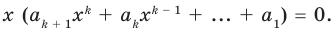
Равенство (4) должно выполняться при всех значениях 
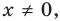
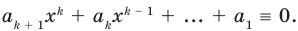
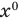
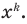
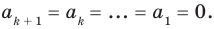
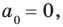
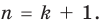
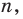
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 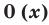
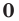
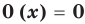
Теорема 3. Если два многочлена 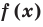
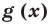
Пусть многочлен 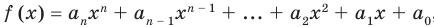
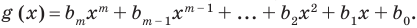
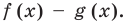
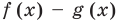
Но 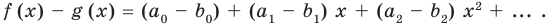
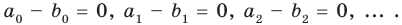
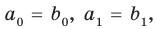
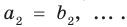
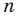
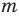
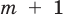
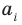
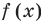
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
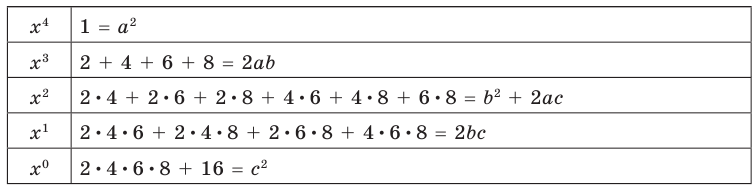
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 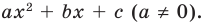
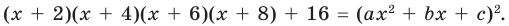
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 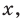
Из первого равенства получаем 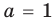
При 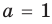
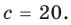
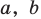
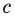
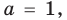
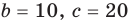
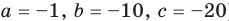
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 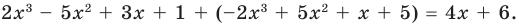
Например, 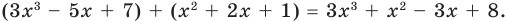
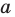
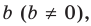
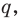
Определение: Многочлен 
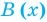
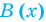

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 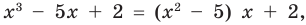
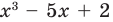
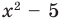
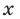
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 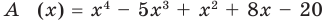
Решение:
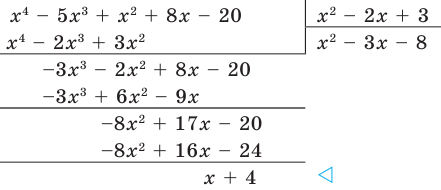
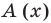
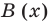
Если обозначить результат выполнения первого шага алгоритма через 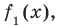
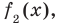
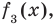
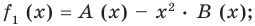
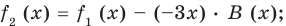
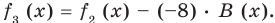
Сложим почленно равенства (1), (2), (3) и получим
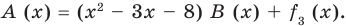
Учитывая, что степень многочлена 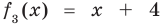
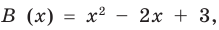
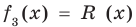
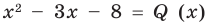
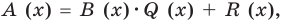
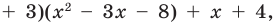
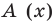
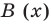
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 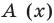
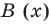
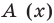
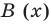
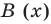
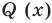
Отметим, что в случае, когда степень делимого 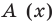
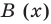
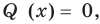
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 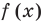
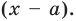
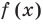
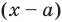
Это равенство выполняется тождественно, то есть при любом значении 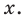
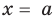
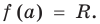
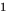
Теорема 1 (теорема Безу). Остаток от деления многочлена 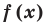
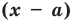
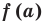
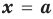
Пример №2
Докажите, что 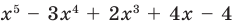
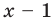
Решение:
► Подставив в 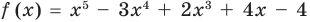
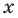
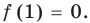
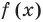

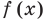

Определение: Число 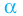
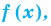
Если многочлен 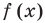

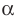
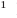
Действительно, если 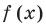
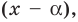

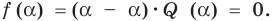
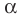
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 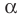
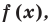
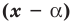
По теореме Безу остаток от деления 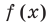

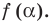
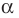
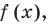
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 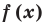
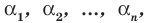
Для доказательства используем метод математической индукции.
При 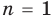
Допустим, что утверждение справедливо при 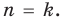
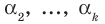
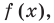
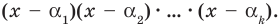
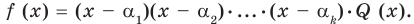
Докажем, что утверждение теоремы справедливо и при 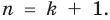
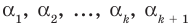
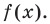
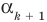
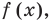
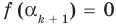
По условию все корни 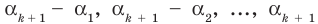
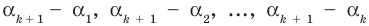
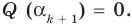
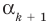
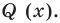
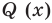
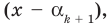
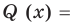
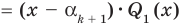
Это означает, что 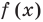
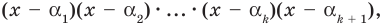
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 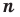
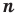
Допустим, что многочлен 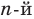
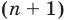
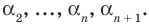
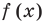
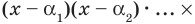
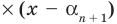
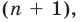
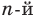
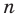
Пусть теперь многочлен 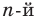
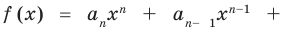
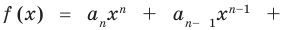
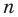
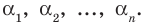
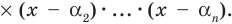
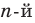
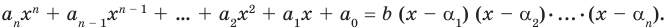
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 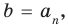
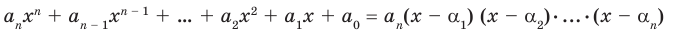
Сравнивая коэффициенты при одинаковых степенях 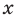
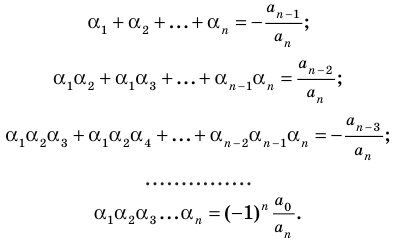
Например, при 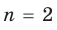
а при
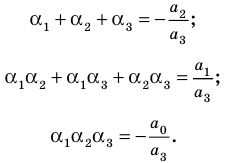
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 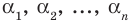
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 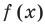
Если многочлен 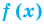
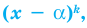
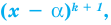


Например, если произведение 
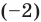
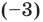
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 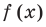
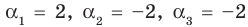
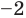
Проверим справедливость формулы (5). В нашем случае: 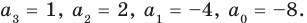
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 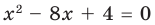
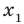
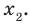
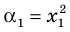
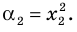
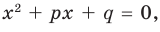
По формулам Виета имеем 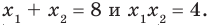
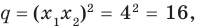
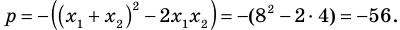
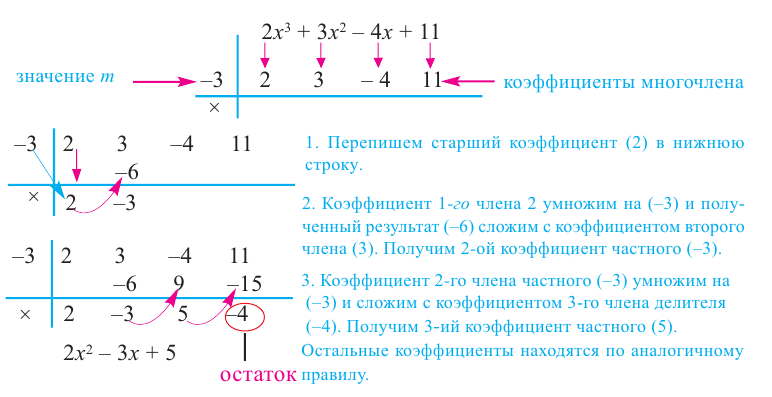
Схема Горнера
Делить многочлен 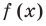
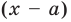
специальной схемы, которую называют схемой Горнера.
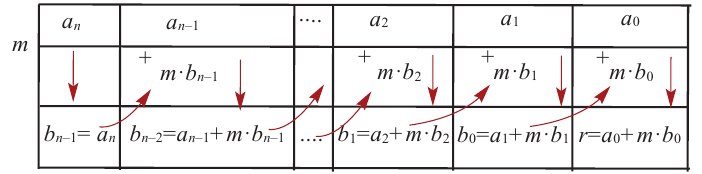
Пусть многочлен 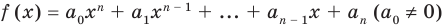
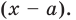
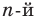
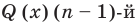
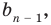
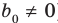
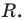
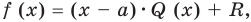
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 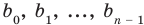
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 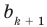
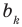
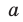
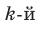
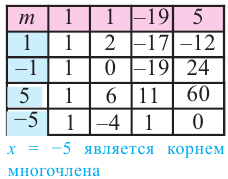
Пример №5
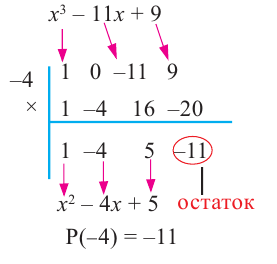
Разделите по схеме Горнера многочлен 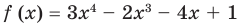
Решение:
► Запишем сначала все коэффициенты многочлена 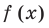
Таким образом,
Пример №6
Проверьте, является ли 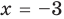
Решение:
► По теореме Безу остаток от деления многочлена 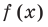
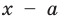
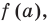
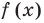
Поскольку 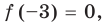
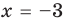
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 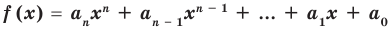
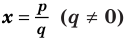
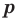
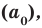
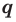
Если 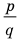
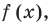
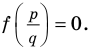
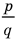
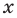
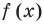
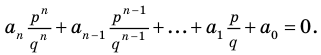
Умножим обе части равенства (1) на 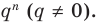
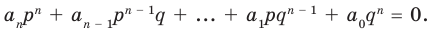
В равенстве (2) все слагаемые, кроме последнего, делятся на 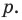
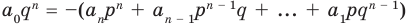
Но когда мы записываем рациональное число в виде 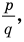
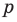
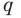
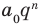
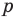
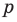
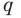
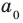
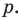
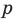
Аналогично все слагаемые равенства (2), кроме первого, делятся на 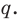
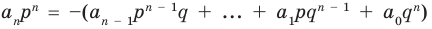
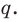
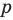
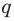
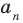
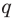
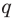
Отметим два следствия из этой теоремы. Если взять 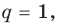
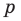
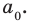
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 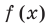
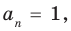
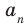
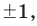
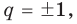
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 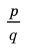
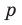
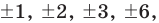
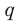
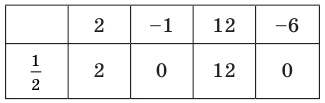
Таким образом, рациональные корни многочлена необходимо искать среди чисел 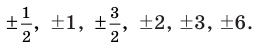
При 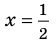
Кроме того, по схеме Горнера можно записать, что
Многочлен 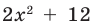
Пример №8
Разложите многочлен 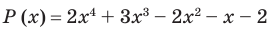
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 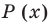

Тогда
Ищем целые корни кубического многочлена 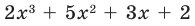
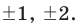
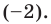
Имеем
Квадратный трехчлен 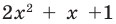
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 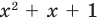
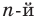
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
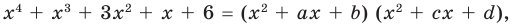
где 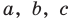
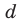
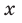
Получаем систему
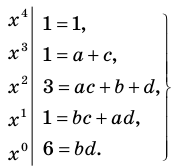
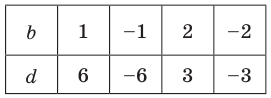
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 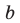
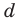
Коэффициенты 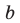
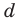
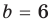
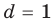
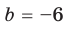
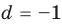
Для каждой пары значений 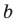
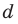
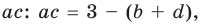
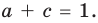
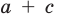
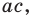
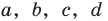
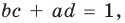
Как видим, системе (4) удовлетворяет набор целых чисел 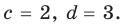
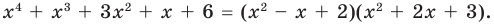
Поскольку квадратные трехчлены 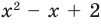
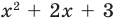
Деление многочлена на многочлен
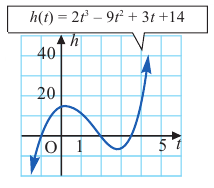
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 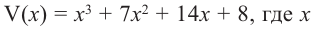
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 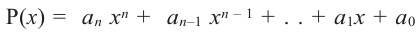
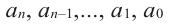
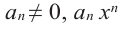
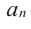
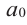
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 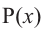
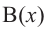
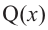
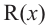
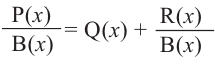
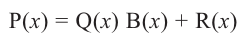
Здесь, степень многочлена 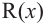
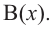
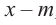
В этом случае:
Пример №10
а) Разделите многочлен 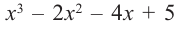
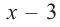
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 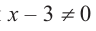
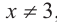
c) Должно выполняться тождество
Пример №11
Разделите 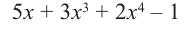
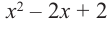
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 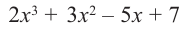
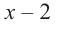
2) На каждом шаге деления делимое делится на старший член делителя, на 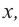
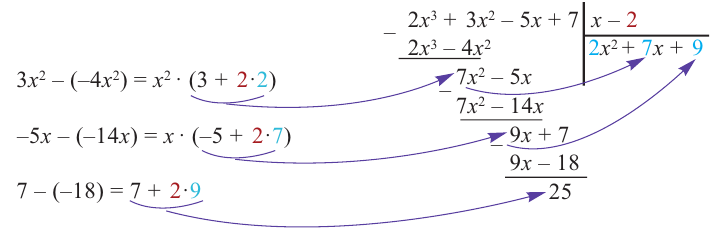
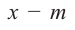
При делении многочлена на двучлен вида 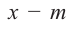
Пример №13
Разделите многочлен 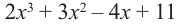
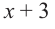
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 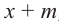
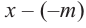
Запишем двучлен 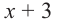
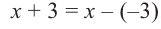
Таким образом, для делимого 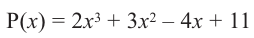
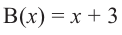
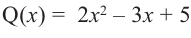
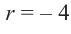
Деление можно записать в виде: 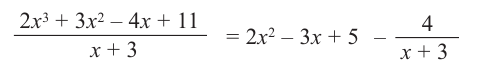
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 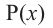
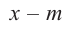
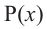
Доказательство: В равенстве 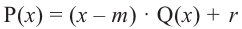
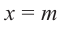
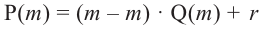
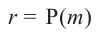
Пример №14
Найдите остаток от деления многочлена 
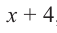
Решение: запишем делитель в виде 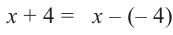
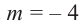
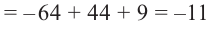
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 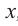
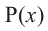
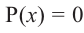
Теорема. Если число 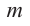
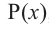
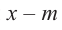
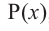
Действительно, если 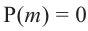
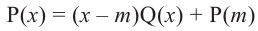
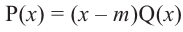
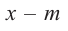
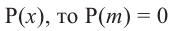
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 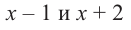
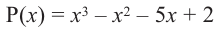
Решение: вычислим значение многочлена 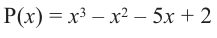
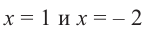
Значит, 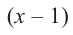
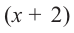
Пример №16
Зная, что 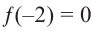
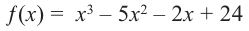
Решение: так как 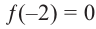
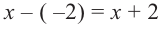
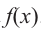
Учитывая, что 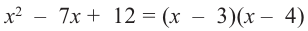
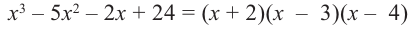
Отсюда получаем, что 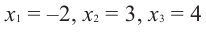
Примечание: Если многочлен задан в виде 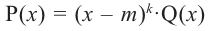
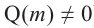
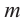
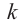
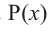
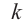
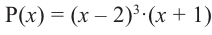
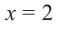
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 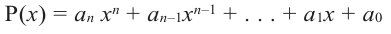
Доказательство. Пусть несократимая дробь 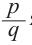
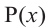
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 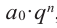
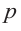
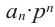
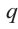
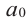
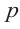
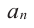
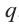
Пример №17
Найдите рациональные корни многочлена 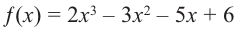
Решение: свободный член 6, старший коэффициент 2.
Для 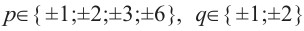
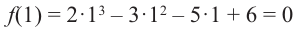
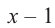
Так как, 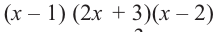
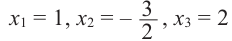
Следствие 1. Если старший коэффициент 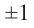
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
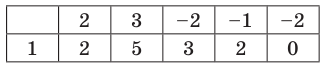
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 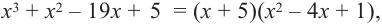
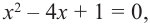
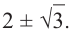
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 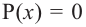
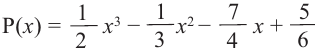
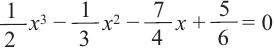
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 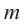
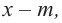
3. Для данного многочлена при помощи синтетического деления на двучлен 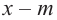
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 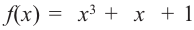
Проверим: 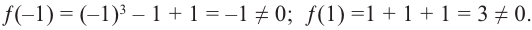
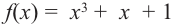
Основная теорема алгебры
Покажем на примере, что многочлен 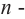
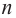
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 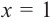
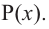
В выражении 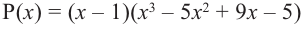
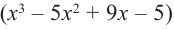
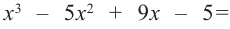
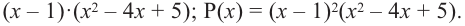
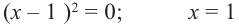
Корни:
Во всех рассмотренных нами примерах уравнение 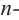
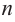
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 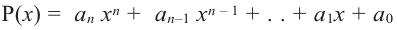
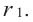
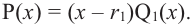
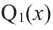
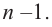
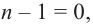
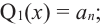
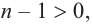
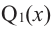
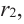
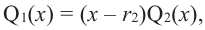
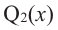
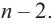
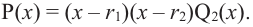
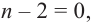
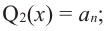
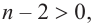
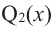
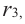
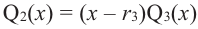
Продолжая процесс 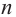
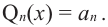
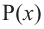
здесь числа 
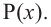
Следствие. Многочлен 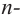
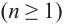
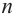
Отметим, что если комплексное число 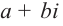
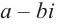
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 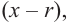
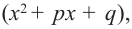
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 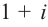
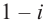
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 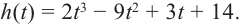
Решение: во всех случаях, кроме значений 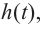
1. Проверим, является ли число 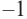
2. Число 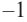
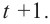
Учитывая, что 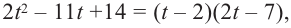
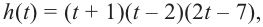
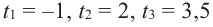
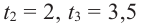
Функция-многочлен
График функции-многочлен
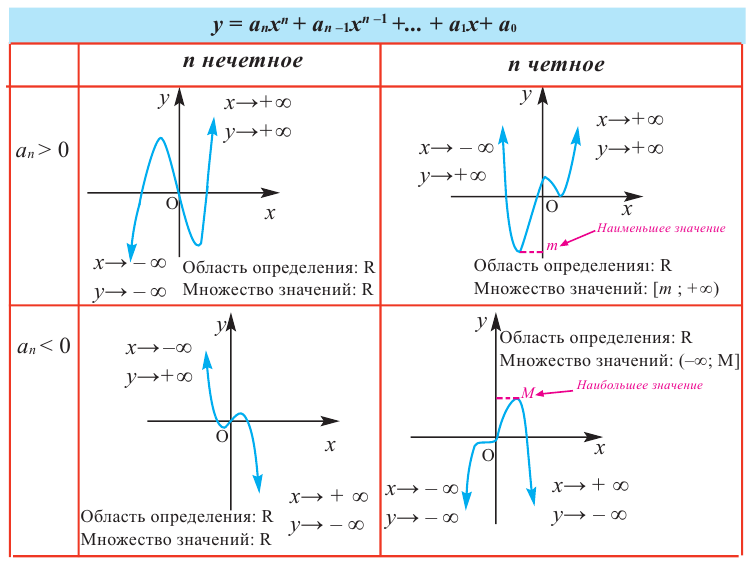
В стандартном виде функция – многочлен записывается как 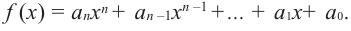
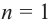
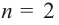
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 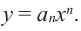
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 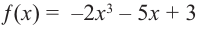
Решение: а) степень многочлена 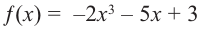
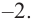
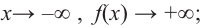
b) степень многочлена 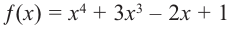
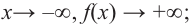
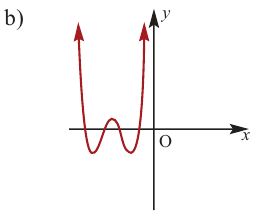
Пример №23
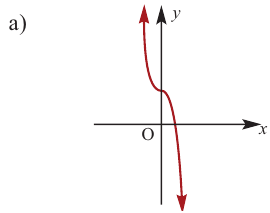
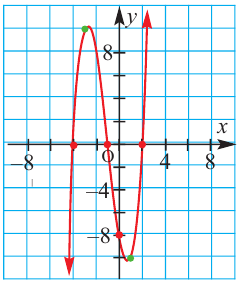
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 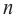
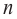
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 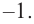
Значит, двучлен 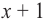
Зная, что 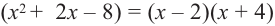
Отсюда находим нули 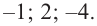
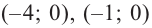
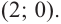
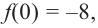
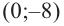
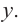
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 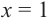
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 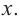
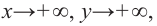
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
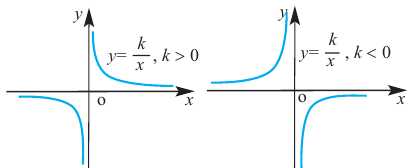
Самым простым примером рациональной функции является функция
График функции 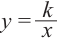
При стремлении значений 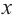
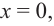
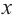
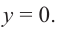
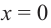
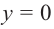
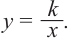
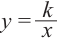
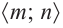
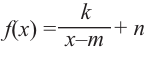
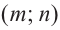
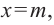
Пример №25
Постройте график функции
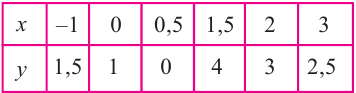
Решение: точки пересечения с осью 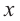
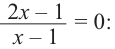
При 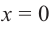
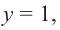
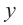
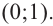
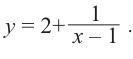
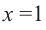
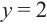
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 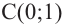
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 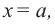
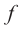
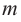
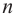
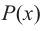
Для 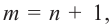
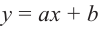
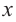
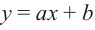
Пример №26
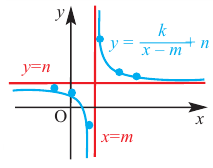
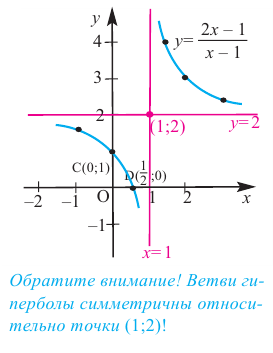
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 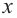
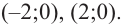
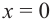
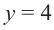
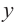
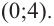
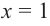
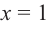
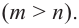
Для больших, но модулю, значений 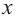
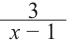
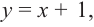
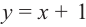
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
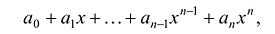
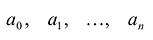
Если коэффициент 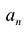
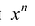
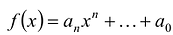
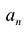
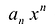
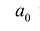
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 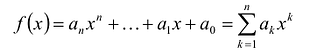
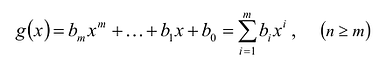
Произведением многочленов 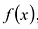
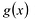
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 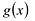
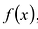
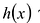
Теорема о делении с остатком
Для любых многочленов 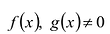
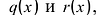
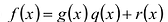
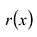
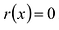
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
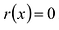
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с – корень многочлена 


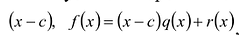
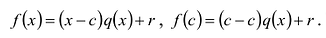

Обратно, пусть (х-с) делит 
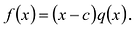
Следствие. Остаток от деления многочлена 
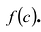
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 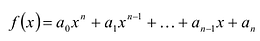
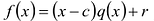
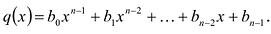
Число с-называется корнем кратности к многочлена 
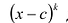

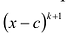

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 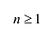
где 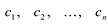

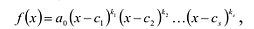
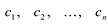

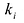
Если многочлен 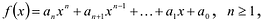
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 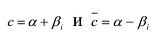


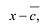
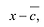

Утверждение 2. Многочлен с действительными коэффициентами степени 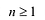
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где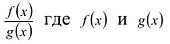
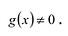

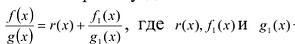
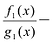
Лемма 1, Если 
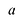
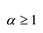
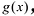
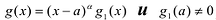
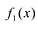
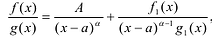
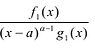
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
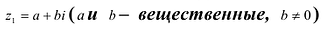
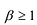
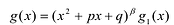
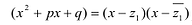
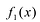
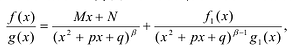
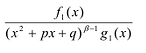
Рациональные дроби вида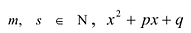
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 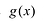
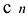
Число неизвестных 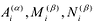
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
Что такое многочлены? Познакомимся с этим понятием из курса математики 7 класс. Мы с вами дадим определение многочленам, рассмотрим какие выражения можно назвать многочленами, а какие нельзя. Разберем что такое многочлен стандартного вида и степень многочлена и решим несколько примеров на определение степени многочлена и приведение подобных слагаемых.
Определение многочлена
Многочленом называют алгебраическую сумму одночленов. То есть многочлен – это алгебраическое выражение, которое записывается в виде суммы одночленов.
Пример многочлена: .
Неправильно
Как отличить многочлен от не многочлена – обратите внимание на варианты неправильного называния не многочлена многочленом:
- Неправильно называть многочленом дробь, например, дробь
не является многочленом. Так как многочлен – это сумма одночленов.
- Неправильно называть многочленом произведение, например:
– не является многочленом, но из этого выражения путем преобразований можно получить многочлен.
Виды многочленов
Среди многочленов выделяют следующие виды многочлены:
- Многочлен состоящий из одного одночлена называется одночленом.
- Многочлен, состоящий из двух одночленов, называется двучленом или биномом.
- Многочлен, состоящий из трех одночленов, называется трехчленом.
Это стандартные называния таких многочленов, многочлен, состоящий из любого произвольного числа одночленов, большего трех, называется просто многочленом.
Стандартный вид многочлена
Если все входящие в многочлен одночлены имеют стандартный вид и в многочлене приведены подобные слагаемые, то такой многочлен называется многочленом стандартного вида.
Приведем пример: выражение является многочленом стандартного вида.
Степень многочлена
Чтобы определить степень многочлена нужно найти одночлен с наибольшей степенью, входящий в его состав. Например, в многочлене наибольшая степень у одночлена
, у которого степень 5. Таким образом, и многочлен будет пятой степени.
Сложение подобных слагаемых
Сумму подобных членов многочлена можно заменить одним членом, если сложить их числовые коэффициенты и оставить буквенную часть. Такое сложение или, иначе, тождественное преобразование, называют приведением подобных слагаемых.
Приведем пример: в многочлене можно сложить подобные слагаемые
и
, тогда мы получим:
и
.
Многочлен можно записать в виде
Примеры решения задач
Задание 1
Определите степень многочлена .
Решение: наибольшая степень у одночлена , значит, степень многочлена – 3.
Задание 2
Приведите подобные слагаемые многочлена: .
Решение: сложим слагаемые одинаковой степени, это и
, а также сложим
и
. Подчеркнем подобные слагаемые одинаковыми чертами. Получаем,
.
Ответ: .
Задание 3
Приведите подобные члены многочлена:
.
Решение: выделим подобные слагаемые и сложим их: .
Ответ: .
Задание 4
Приведите подобные члены многочлена:
.
Решение: подчеркнем подобные слагаемые и выполним сложение: .
Ответ: .
Задание 5
Приведите подобные члены многочлена:
.
Решение: .
Ответ:
Задание 6
Приведите подобные члены многочлена:
Решение: .
Ответ: .
Задание 7
Приведите подобные члены многочлена: .
Решение: .
Ответ: .
Задание 8
Приведите подобные члены многочлена: .
Решение: .
Ответ:
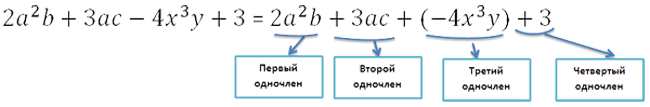
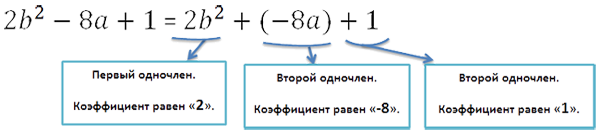





![{displaystyle deg[qcirc p(x)]=deg[pcirc q(x)]=deg p(x)deg q(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af75f6c342e8b1b362f57201f20ccaa9e1480fe6)