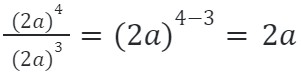|
Например : 2^3 x 4^5 = ? Не знаю удачный ли пример,но что тут надо делать?При умножении и делении надо степени вычитать и складывать,а тут что?
В общем случае с этим ничего не сделать, в вашем конкретном примере можно 4 представить как 2 во 2-й степени. Получится (2^2)^5. Далее, т.к. при возведении степени в степень показатели степеней перемножаются, получаем 2^3 x 2^10 = 2^13 = 8192. Т.е. числа нужно приводить ко одинаковому основанию или показателю степени. Тут 2 правила: X^a * X^b = X^(a+b) X^a * Y^a = (XY)^a. модератор выбрал этот ответ лучшим
Galina7v7 7 лет назад У вас не сложение , или вычитание , а умножение. И это очень меняет дело* В данном примере нужно привести 4 к степени двойки : 4 =2^(2) , тогда 2^(3) * 4^(5) = 2^(3) * [2^(2)]^5 = 2^(3 * 2^(10) = 2 ^ (3+10) = 2 ^ (13) или 2 в 13 степени. Если бы был пример на сложение ,то есть : 2 ^ (3) + 4 ^ (5) = [2 ^( 3) + (2 )]^ 2 ^ 5 = 2 ^ (3) + 2 ^( 10)= 2 ^(3) *[1+2 ^( 7)]. И это совсем другой результат.А правила действий со степенями такие : a ^ (m) * a ^ (n) = a ^ (m+n)a ^(m) a ^ (n) = a ^ (m-n)a^ (m )+ a ^( n) = a ^(m) *[a ^(m-n)+1}Вот это правило очень важное,потому что когда степени стоят как слагаемые,то их нельзя иначе преобразовать,как только вынести общий множитель за скобки. ({a ^ (m)}^n= a ^ (m*n)
Ксарфакс 5 лет назад Если в выражении присутствует возведение в степень, то алгоритм действий различается для умножения/деления и для сложения/вычитания. Начнём с самого простого – умножение и деление степеней с одинаковым основанием. 1) Умножение – основание остаётся тем же, а показатели степени складываем. 2) Деление – основание оставляем, а из показателя степени делимого вычитаем показатель степени делителя.
В этой ситуации затруднений вообще быть не должно. При умножении и делении степеней с разными основаниями порядок алгоритм такой – приводим их к одному основанию (если это можно сделать), а затем выполняем действия по вышеприведённым правилам.
Если основания разные, но при этом показатель степени один и тот же, то нужно перемножить основания и возвести их в степень.
Другое дело, если требуется сложить или вычесть степени. Здесь ситуация разная. Если показатель степени у чисел один и тот же, то можно воспользоваться формулами сокращённого умножения для суммы и разности степеней. В некоторых случаях можно попробовать общий множитель выносится за скобки.
Ну и последний вариант (если первые два способа не применимы) – возводим каждое число в степень и складываем/вычитаем. renard 6 лет назад В вашем примере 2^3•4^5 нужно найти произведение степеней с разными основаниями. Потребуется несколько действий совершить:
Со сложением чисел в одной степени, как и с вычитанием, занимаемся расчетами на калькуляторе или в столбик на бумажке. Хотя есть возможность использовать известные из школьной алгебры формулы сокращенного умножения для вычитания квадратов, для сложения или вычитания кубов. Так можно хоть от степеней избавиться или понизить их. a^2-b^2=(a-b)•(a+b) – так упрощаем разность квадратных чисел. a^3-a^3 = (a+b)•(a^2-ab+b^2)или a^3+b^3=(a-b)•(a^2+ab+b^2) и с неудобными третьими степенями можно распрощаться.
В общем случае ничего с таким умножением сделать нельзя. То есть если требуется умножить 2 в квадрате на 3 в кубе, то это не значит, что мы должны 2 умножить на 3 и возвести результат в 5 степень – ответ получится неверный. Приходится возводить 2 в квадрат, а 3 в куб и только потом перемножать числа. Но если требуется 2 в произвольной степени умножить на 4 в произвольной степени, то мы представляем 4 как 2 в квадрате и просто складываем степени. Если же мы складываем или вычитаем два числа возведенных в степени, то тут нет никакого правила – надо возводить и складывать (вычитать) результат: а^3 + b^4 не упростить да и не надо.
ZoRRoO 8 лет назад На вашем примере нужно привести к одной основе, то есть 4 – это 2^2. Поэтому запишем выражение следующим образом 2^3 x 4^5 = 2^3 x (2^2)^5. Теперь нам нужно избавиться от этих скобочек. Мы знаем, что по правилу степени просто перемножаются, поэтому, у нас получится следующее выражение: 2^3 x 2^10. А теперь у нас есть единая основа, значит мы можем просто сложить степени. Получится такое выражение: 2^13. Ответ будет 8192. Итак, на представленном вами примере мы использовали всего лишь 2 правила, а именно сложение степеней, когда есть одна основа, и умножение их, когда мы возводим одну степень в другую. Конь В Пальто 10 лет назад Ничего кроме выполнения отдельных операций согласно их приоритету, вы тут не сделаете. Если вам нужно сложить два разных числа в разных степенях, то сначала каждое число вы возводите в свою степень и после этого выполняете сложение. Если у двух слагаемых в основании одно число в разных степенях, можно вынести общее кратное: Например, а^x+y + а^x = а^x * (а^y + 1) Если основания разные, но степень одна, то в некоторых простых частных случаях можно воспользоваться алгебраическими формулами вроде: а^2-b^2= (а-b) * (a+b). Но это очень редкие совпадения, расчитывать на которые не стоит.
Azamatik 5 лет назад Пример: 2^3 х 4^5. Для решения этого уравнения нужно привести их к одинаковому основанию: представить 4 как 2 в квадрате (2^2). Изначально у нас было 4^5 > (2^2)^5. Степени умножаем и получаем 2^10. Теперь можно решить это уравнение; 2^3 х2^10. Складываем степени и получаем 2^13. Подобные уравнения решаются именно так: Если основания одинаковые, то складываем степени. Если же показатели степени одинаковые, то нужно основания перемножить и полученный результат возвести в степень.
Odessitka 8 лет назад Если умножать степени с одинаковым основанием, то показатели степени складываются: Например: 2^2 х 2^4 = 2^6 = 64 Если делить степени с одинаковым основанием, то показатели степени вычитаются: Например: 2^4 / 2^2 = 2^2 = 4. Если же умножать или делить степени с разным основанием, то нужно сначала возвести основание в степень, а потом совершать умножение или деление. В вашем случае 2^3 x 4^5 = 8 х 1024 = 8192.
Лолочка611 8 лет назад При умножении степеней, которые имеют одинаковые основания – числа степеней складываются. При делении степеней, которые имеют одинаковые основания – числа степеней вычитаются. А вот если умножать, либо делить степени, которые имеют разные основания, нужно выполнить следующие действия:
Знаете ответ? |
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
23+ 34= 8 + 81= 89
63— 33= 216 — 27 = 189
- Если есть скобки — начинать вычисления нужно внутри них
- Только потом возводим этот результат из скобок в степень
- Затем выполняем остальные действия: сначала умножение и деление по порядку (слева направо), а в конце — сложение и вычитание по порядку (слева направо)
Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 23+ 24= 8 + 16= 24
Сложение степеней с разными основаниями
В целом это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые показатели. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 34+ 54=81 + 625 = 706
- 14+ 72= 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно так же, как и в предыдущем примере. Если показатели степени одинаковые, а основания разные — нельзя сложить основания и затем эту сумму возводить в степень.
- 63+ 33= 216 + 27 = 243
В уравнениях с этим все проще. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.
- 2a2 + 3a2 = 5a2
2,3, 5 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
- 63— 33= 216 — 27 = 189
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые показатели степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 54— 44= 625 — 256 = 369
- 74— 32= 2401 — 9 = 2392
Вычитание степеней с одинаковыми показателями
Все точно так же, как и со сложением. Если показатели степени одинаковые, а основания разные — нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
- 63— 33= 216 — 27 = 189
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a2) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a2.
- 5a2 — 3a2 = 2a2
5, 3, 2 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Умножение и деление степеней
Здесь всё не так однозначно, как со сложением и вычитанием — общие правила для всех случаев выделить не получится. Все зависит от оснований и показателей степеней, с которыми нужно выполнить манипуляции.
Например, действия со степенями с разными основаниями будут отличаться от действий с числами, у которых основания одинаковые. Работа с показателями — одинаковыми и разными — тоже отличается. Давайте разбираться.
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
- an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35 + 2 = 37 = 2 187
- 28 · 81= 28 · 23 = 28 + 3 = 211 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
- 33 · 52 = 27·25 = 675
Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- an : bn = (a : b)n , где
a, b — основание степени, любые числа, b ≠ 0,
n — показатель степени, натуральное число
Пример:
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
- 33 ÷52 = 27÷25 = 1,08
Степень с отрицательным показателем и её свойства
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
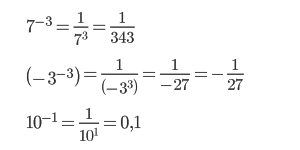
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
- a3÷a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
am · an = am+n
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
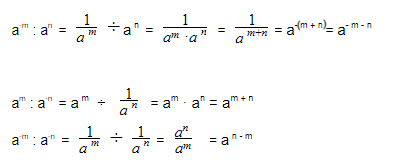
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
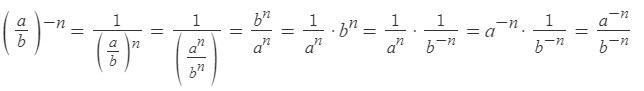
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
243 = 3 × 3 × 3 × 3 × 3 = 35
- Формулы для квадрата и куба бинома
- Формулы для четвёртой и пятой степени бинома
- Треугольник Паскаля
- Формула для n-ой степени бинома
- Примеры
Формула для квадрата и куба бинома
Сумма или разность двух выражений образует двучлен, который также называют биномом. Примеры биномов: x+y, $1+k^2,2mq^2-5z,100a-17b^2 c^3$ и т.д.
Формулы для квадрата и куба бинома мы уже получили в §21 и §23 данного справочника.
$ (a+b)^2 = a^2+2ab+b^2, qquad (a-b)^2 = a^2-2ab+b^2$
$(a+b)^3 = a^3+3a^2 b+3ab^2+b^3, qquad (a-b)^3 = a^3-3a^2 b+3ab^2-b^3$
Формулы для четвёртой и пятой степени бинома
Выведем формулы для 4-й степени:
$(a+b)^4 = (a+b) (a+b)^3 = a(a+b)^3+b(a+b)^3 =$
$ = a(a^3+3a^2 b+3ab^2+b^3 )+b(a^3+3a^2 b+3ab^2+b^3 ) =$
$= a^4+3a^3 b+3a^2 b^2+ab^3+a^3 b+3a^2 b^2+3ab^3+b^4 =$
$= a^4+4a^3 b+6a^2 b^2+4ab^3+b^4$
Для разности в 4-й степени нужно только поменять знаки при нечётных степенях b.
Получаем:
$(a+b)^4 = a^4+4a^3 b+6a^2 b^2+4ab^3+b^4$
$(a-b)^4 = a^4-4a^3 b+6a^2 b^2-4ab^3+b^4$
Теперь выведем формулы для 5-й степени:
$(a+b)^5 = (a+b) (a+b)^4 = a(a^4+4a^3 b+6a^2 b^2+4ab^3+b^4 )+$
$+b(a^4+4a^3 b+6a^2 b^2+4ab^3+b^4 ) =$
$= a^5+4a^4 b+6a^3 b^2+4a^2 b^3+ab^4+a^4 b+4a^3 b^2+6a^2 b^3+4ab^4+b^5 =$
$= a^5+5a^4 b+10a^3 b^2+10a^2 b^3+5ab^4+b^5$
Для разности в 5-й степени нужно только поменять знаки при нечётных степенях b.
Получаем:
$(a+b)^5 = a^5+5a^4 b+10a^3 b^2+10a^2 b^3+5ab^4+b^5$
$(a-b)^5 = a^5-5a^4 b+10a^3 b^2-10a^2 b^3+5ab^4-b^5$
Треугольник Паскаля
Коэффициенты при членах разложения биномов постепенно становятся больше. Их рост можно представить с помощью треугольника Паскаля.

$$(a pm b)^1 = a pm b$$ $$(apmb)^2 = a^2pm2ab+b^2$$ $$(apmb)^3 = a^3pm3a^2 b+3ab^2±b^3$$ $$(apmb)^4 = a^4pm4a^3 b+6a^2 b^2pm4ab^3+b^4$$ …
В этом треугольнике коэффициенты этажом ниже – это сумма соседних коэффициентов этажом выше; на рисунке каждая сумма обозначена знаком «+» между стрелочками.
Формула для n-ой степени бинома
Теперь для n-й степени бинома можем записать:
$$ (a + b)^n = a^n+C_1^n a^{n-1} b + C_2^n a^{n-2} b^2 + ⋯ + b^n $$
где $C_i^n$ – биномиальные коэффициенты, которые для небольших степеней можно найти с помощью треугольника Паскаля.
Формула для разности немного сложней:
$$ (a – b)^n = a^n-C_1^n a^{n-1} b + C_2^n a^{n-2} b^2 – C_3^n a^{n-3} b^3 +⋯+(-1)^n b^n $$
Биномиальные коэффициенты играют большую роль в современной математике. В общем случае для них есть расчётная формула, которую мы выучим позже.
В общем случае для них есть расчётная формула, которую мы выучим позже (см. §36 справочника для 9 класса)
Биномиальные коэффициенты играют большую роль в современной математике. В общем случае для них есть расчётная формула, которую мы выучим позже.
Примеры
Пример 1. Представьте в виде многочлена:
а) $(1+k)^4$
Коэффициенты по треугольнику Паскаля: $1 quad 4 quad 6 quad 4 quad 1$
Получаем:
$$(1+k)^4 = 1+4k+6k^2+4k^3+k^4$$
б) $(1-k)^4$
Коэффициенты по модулю те же, знаки поменяются перед слагаемыми с нечётными степенями k:
$$(1-k)^4 = 1-4k+6k^2-4k^3+k^4$$
в) $(a+b)^7$
Коэффициенты по треугольнику Паскаля: $1 quad 7 quad 21 quad 35 quad 35 quad 21 quad 7 quad 1$
Получаем:
$$(a+b)^7 = a^7+7a^6 b+21a^5 b^2+35a^4 b^3+35a^3 b^4+21a^2 b^5+7ab^6+b^7$$
г) $(a-b)^7$
Коэффициенты по модулю те же, знаки поменяются перед слагаемыми с нечётными степенями b:
$$ (a-b)^7 = a^7-7a^6 b+21a^5 b^2-35a^4 b^3+35a^3 b^4-21a^2 b^5+7ab^6-b^7 $$
Пример 2. Упростите выражение:
а) $(x+y)^4-(x-y)^4 = (x^4+4x^3 y+6x^2 y^2+4xy^3+y^4 )-$
$-(x^4-4x^3 y+6x^2 y^2-4xy^3+y^4 ) = 8x^3 y+8xy^3$
б) $(x+y)^4+(x-y)^4 = (x^4+4x^3 y+6x^2 y^2+4xy^3+y^4 )+$
$+(x^4-4x^3 y+6x^2 y^2-4xy^3+y^4 ) = 2x^4+126x^2 y^2+2y^4 $
в) $(x+y)^5-(x-y)^5 = (x^5+5x^4 y+10x^3 y^2+10x^2 y^3+5xy^4+y^5 )-$
$-(x^5-5x^4 y+10x^3 y^2-10x^2 y^3+5xy^4-y^5 ) = 10x^4 y+20x^2 y^3+2y^5$
г) $(x+y)^5+(x-y)^5 = (x^5+5x^4 y+10x^3 y^2+10x^2 y^3+5xy^4+y^5 )+$
$+(x^5-5x^4 y+10x^3 y^2-10x^2 y^3+5xy^4-y^5 ) = 2x^5+20x^3 y^2+10xy^4$
Загрузить PDF
Загрузить PDF
Степень, а точнее показатель степени, говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя.[1]
Чтобы найти сумму степеней, следует уметь определить, вручную либо на калькуляторе, значение каждого слагаемого. При сложении переменных со степенями необходимо знать правила суммирования схожих членов.
-

1
Вычислите первое степенное выражение. Оно состоит из основания (крупное число внизу) и показателя (меньшее по размеру число справа вверху) степени. Показатель степени определяет, сколько раз следует умножить основание само на себя (например,
).[2]
-

2
Вычислите второе степенное выражение. Для этого умножьте основание степени на само себя столько раз, сколько указано в показателе степени.
-

3
Сложите полученные значения. Таким образом вы найдете сумму двух степенных выражений.
Реклама
-

1
Найдите на калькуляторе клавишу степени. Как правило, на ней написано
,
или
с пустым квадратом, который обозначает показатель степени. Данный метод не годится, если в вашем калькуляторе нет опции возведения в степень.
-

2
Введите первое степенное выражение. Для этого введите сначала основание степени (более крупное число), а затем показатель степени.
-

3
Нажмите клавишу сложения. В результате у вас получится значение первого слагаемого. После этого не нужно нажимать знак равенства (клавишу
).
-

4
Введите второе степенное выражение. Для этого введите сначала основание степени (более крупное число), а затем показатель степени.
-

5
Нажмите знак равенства (клавишу
). В результате у вас получится сумма двух степенных выражений.
Реклама
-

1
Найдите слагаемые с одинаковыми основаниями и показателями степени. Основание имеет вид более крупного числа (или переменной) внизу, а показатель степени стоит справа вверху.
-

2
Сложите слагаемые с одинаковыми основаниями и показателями степени.[5]
При работе с переменными можно складывать лишь те члены, у которых одинаковые основания и показатели степени. То есть одинаковыми должны быть ОБЕ эти части. -

3
Сложите коэффициенты при схожих членах. Помните о том, что при отсутствии коэффициента он равен
. НЕ складывайте показатели степени. Показатель степени должен остаться прежним.
-

4
Запишите окончательное упрощенное выражение. Помните о том, что складывать следует лишь коэффициенты при членах с одинаковым основанием И показателем степени, причем основание и показатель останутся прежними.
Реклама
Что вам понадобится
- Карандаш
- Лист бумаги
- Калькулятор
Похожие статьи
Об этой статье
Эту страницу просматривали 223 722 раза.