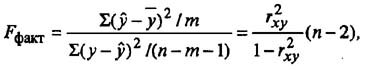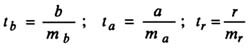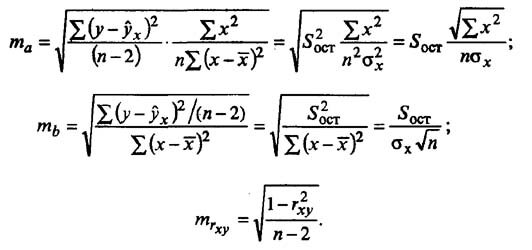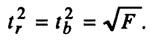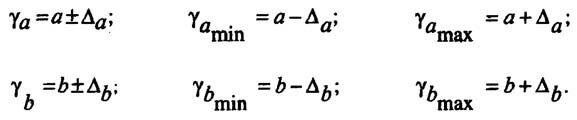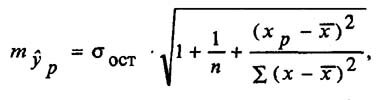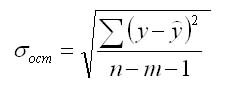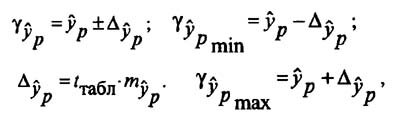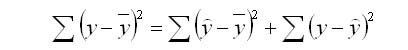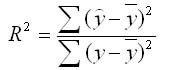Как найти степень свободы для критерия фишера - Сайт, где вы сможете решить свои вопросы

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;
m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

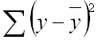
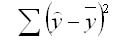
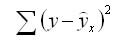
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R² > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

Источник

Время на прочтение
4 мин

Количество просмотров 4.4K

Здравствуй, Хабр!

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

$y_{i}text{=},beta_{0}text{+}beta_{1}text{x},text{+},varepsilon_{i} (1)$

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

$beta_{1}pm t_{left(frac{alpha}{2},,n-2right)}cdotfrac{{sqrt[]{MSE}}text{}}{sumlimits_{i=1}^{n}left(x_{i}-overline{x}right)^{2}},, (2)$

А значит не можем сказать ничего о целесообразности использования коэффициента beta_1 в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Рисунок 1 – простая линейная регрессия

Количество степеней свободы – количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

$s^{2}=frac{sum_{i=1}^{n}left(y_{i}- overline{y}right)^{2}}{df}=frac{sum_{i=1}^{n}left(y_{i}- overline{y}right)^{2}}{n-1} (3)$

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Рисунок 3

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле $mu_{Y}=beta_{0}+beta_{1}x$ . И каждое выборочное среднее может быть оценено $hat{y}_{i}=,b_{0},+,b_{1}x_{i}$ . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE – standard error of estimate) вид:

$SSE=MSE=frac{sum_{i=1}^{n}left(y_{i,}-hat{y}_{i}right)^{2}}{n-2} (4)$

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле $hat{y}_{i}=,b_{0},+,b_{1}x_{i}$ . Квадратные корень формулы (4) – ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

где n – число наблюдений, k – число независимых переменных.

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

$sum_{i=1}^{n}left(y_{i}-bar{y}right)^{2}=sum_{i=1}^{n}left(hat{y_{i}}-,bar{y}right)^{2},+,sum_{i=1}^{n}left(y_{i}-,hat{y_{i}}right)^{2} , (6)$

где $sum_{i=1}^{n}left(y_{i}-bar{y}right)^{2},text{-};text{SSTO};text{(Total};text{sum};text{of};text{squares)}$ ,

$sum_{i=1}^{n}left(hat{y_{i}}-bar{y}right)^{2},text{-};text{SSR};text{(Regression};text{Sum};text{of};text{squares)}$ ,

$sum_{i=1}^{n}left(y_{i}-hat{y_{i}}right)^{2},text{-};text{SSE};text{(Error};text{sum};text{of};text{squares)}$

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .

Масштабируем SSE и SSR с учетом их степеней свободы:

$MSE,=,frac{sum_{i=1}^{n}left(y_{i}-hat{y_{i}}right)^{2}}{n-2}=frac{SSE}{n-2} (7)$ $MSR,=,frac{sum_{i=1}^{n}left(bar{y_{i}}-hat{y_{i}}right)^{2}}{1}=frac{SSR}{1} (8)$

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

$F,=frac{MSR}{MSE} (9)$

Формула (9) используется при проверке нулевой гипотезы $H_{0}:beta_{1}=0$ при альтернативной гипотезе $H_{1}:beta_{1}neq0$ в случае линейной регрессионной модели вида (1).

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Шаги:

Определим “полную” модель: $y_{i}^{F}=left(beta_{0}+beta_{1}x_{i1}+...+beta_{k}x_{ik}right),+,varepsilon_{i}$ (10)
Определим “укороченную” модель: $y_{i}^{R}=left(alpha_{0}+alpha_{1}x_{i1}+...+alpha_{t}x_{it}right),+,varepsilon_{i}$ (11)
Вычисляем сумму квадратов ошибок для каждой модели:

$text{SSE(F)};=,sum_{i=1}^{n}left(y_{i}-widehat{y_{i}^{F}}right)^{2}$ (12)

$text{SSE(R)};=,sum_{i=1}^{n}left(y_{i}-widehat{y_{i}^{R}}right)^{2}$ (13)
Определяем количество степеней свобод $df_{F},,df_{R}$
Рассчитываем F-статистику:

$F,=,left(frac{SSEleft(Rright)-SSEleft(Fright)}{df_{R}-df_{F}}right),div,left(frac{SSEleft(Fright)}{df_{F}}right)$ (14)

Нулевая гипотеза – “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза – “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

$R^{2}=,frac{SSR}{SSTO}=1-frac{SSE}{SSTO} (15)$

Из формулы (15) выразим SSE(F):

$text{SSE(F)};text{=};left(1-R^{2}right)SSTO (16)$

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

$F,=,left(frac{SSEleft(Rright)-SSEleft(Fright)}{df_{R}-df_{F}}right),div,left(frac{left(1-R_{F}^{2}right)SSTO}{df_{F}}right) (14a)$

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

$F,=,left(frac{left(-1,+,frac{SSEleft(Rright)}{SSTO}right)+left(1-frac{SSEleft(Fright)}{SSTO}right)}{df_{R}-df_{F}}right),div,left(frac{left(1-R^{2}right)}{df_{F}}right) (14б)$

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

$F,=,left(frac{R_{F}^{2}-R_{R}^{2}}{df_{R}-df_{F}}right),div,left(frac{left(1-R_{F}^{2}right)}{df_{,F}}right) (14 в)$

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем beta_0 ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид $y_{i}^{R}=beta_{0}+varepsilon_{i}$ . Следовательно $R_{R}^{2}=0, df_{R}=n-1, df_{F}=n-k$ . Используя формулу (14.в), получим

$F,=,left(frac{R_{F}^{2}}{k-1}right),div,left(frac{left(1-R_{F}^{2}right)}{n-k}right),sim,Fleft(k-1,,n-kright)$

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501

Теги:

F-тест
Отбор моделей
Линейная регрессия

Хабы:

Математика
Статистика

Источник

Критерий
Фишера позволяет сравнивать величины
выборочных дисперсий двух рядов
наблюдений. Для вычисления
нужно
найти отношение дисперсий двух выборок,
причем так, чтобы большая по величине
дисперсия находилась бы в числителе, а
меньшая знаменателе. Формула вычисления
по критерию Фишера F такова:

Где

Поскольку,
согласно условию критерия, величина
числителя должна быть больше или равна
величине знаменателя, то значение
всегда
будет больше или равно единице, т.е..
Число степеней свободы определяется
также просто:для
первой (т.е. для той выборки, величина
дисперсии которой больше) идля
второй выборки. В таблице 18 Приложения
6 критические значения критерия Фишеранаходятся
по величинам(верхняя
строчка таблицы) и(левый
столбец таблицы).

Пример:
В двух третьих классах проводилось
тестирование умственного развития по
тесту ТУРМШ десяти учащихся. Полученные
значения величин средних достоверно
не различались, однако психолога
интересует вопрос – есть ли различия в
степени однородности показателей
умственного развития между классами.

Для
критерия Фишера необходимо сравнить
дисперсии тестовых оценок в обоих
классах. Результаты тестирования
представлены в табл. 11.

Таблица
11

№ учащихся	Первый класс X	Второй класс Y
1	90	41
2	29	49
3	39	56
4	79	64
5	88	72
6	53	65
7	34	63
8	40	87
9	75	77
10	79	62
Суммы	606	636
Среднее	60,6	63,6

Как
видно из табл. 11, величины средних в
обеих группах практически совпадают
между собой 60,6
63,
6 и величина t – критерия Стьюдента
оказалась равной 0, 347 и незначимой.

Рассчитав
дисперсии для переменных X и Y, получаем

Тогда,
по формуле для расчета по F – критерию
Фишера находим:

По
табл. 18 приложения 6 для F – критерия при
степенях свободы в обоих случаях равных
df= 10 – 1 = 9 находим:

3,18
для P
0,05

5,35
для P
0,01

Строим
“ось значимости”:

Таким
образом, полученная величина
попала
в зону неопределенности. В терминах
статистических гипотез можно утверждать,
что Н(гипотеза о сходстве) может быть отвергнута
на уровне 5%, а принимается в этом случае
гипотеза Н.
Психолог может утверждать, что по степени
однородности такого показателя, как
умственное развитие, имеется различие
между выборками из двух классов.

Для
применения критерия F Фишера необходимо
соблюдать следующие условия:

1.
Измерение может быть проведено в шкале
интервалов и отношений.

2.
Сравниваемые выборки должны быть
распределены по нормальному закону.

8.6. Корреляционный анализ

Корреляцией
называют зависимость между двумя
переменными величинами.

Переменная
– это любая величина, которая может быть
измерена и чье количественное выражение
может варьировать.

При
изучении корреляций стараются установить,
существует ли какая-то связь между двумя
показателями в одной выборке (например,
между ростом и весом детей или между
уровнем IQ и школьной успеваемостью)
либо между двумя различными выборками
(например, при сравнении пар близнецов),
и если эта связь существует, то увеличение
одного показателя сопровождается
возрастанием (положительная корреляция)
или уменьшением (отрицательная корреляция)
другого.

Коэффициент
корреляции
– это величина, которая может варьировать
в пределах от +1 до -1. В случае полной
положительной корреляции этот коэффициент
равен +1, а при полной отрицательной -1.

В
случаи, если коэффициент корреляции
равен 0, обе переменные полностью
независимы друг от друга.

В
гуманитарных науках корреляция считается
сильной, если ее коэффициент выше 0,60;
если же он превышает 0,90, то корреляция
считается очень сильной.

Можно
выделить несколько видов корреляционного
анализа: линейный, ранговый, парный и
множественный. Мы рассмотрим два вида
корреляционного анализа – линейный и
ранговый.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Критерий Фишера и критерий Стьюдента в эконометрике

Таблицы по нахождению критерия Фишера и Стьюдента

Критерии Стьюдента

Видео лекциий по расчету критериев Фишера и Стьюдента

Определение доверительных интервалов

1. Роль степеней свободы (degree of freedom) в статистике

2. Анализ дисперсии, F-тест

3. Выбор линейной регрессионной модели

3 Проверка значимости линейной регрессии

Заключение

8.6. Корреляционный анализ

Вам также может понравиться

Как найти модуль средней скорости движения тела

Как составить план по страховому делу

Советы как найти невесту

Добавить комментарий Отменить ответ