Как найти степень точки относительно окружности

У этого термина существуют и другие значения, см. Степень точки.

Степень точки относительно окружности — величина , где — расстояние от точки до центра окружности, a — радиус окружности.
По этому определению точки внутри круга имеют отрицательные степени, точки вне круга имеют положительные степени, а точки на окружности имеют нулевую степень. Для точки, лежащей вне окружности, из теоремы Пифагора следует, что степень точки относительно окружности есть квадрат длины касательной, проведённой из данной точки к данной окружности.
Степень точки также известна как степень окружности или степень круга относительно точки.

Свойства[править | править код]

Связанные определения[править | править код]

• Для двух не концентрических окружностей геометрическое место точек Р, для которых степени относительно обеих окружностей равны, является прямой, называемой радикальной осью окружностей.

• Для трёх окружностей, центры которых не лежат на одной прямой существует единственная точка, такая, что её степени относительно всех трёх окружностей равны. Эта точка называется радикальным центром трёх окружностей.

• Со степенью точки относительно окружности тесно связано понятие Инверсное расстояние.

История[править | править код]

Термин «степень» в этом значении был впервые употреблён Якобом Штейнером.

Вариации и обобщения[править | править код]

• Аналогично определяется степень точки относительно сферы в -мерном евклидовом пространстве.

Литература[править | править код]

• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Я. П. Понарин. §3.1 Степень точки относительно сферы // Элементарная геометрия. — М.: МЦНМО, 2006. — Т. 2. — С. 146. — 256 с. — 2000 экз. — ISBN 5-94057-223-5.

См. также[править | править код]

• Касательная прямая к окружности
• Окружность
• Радикальная ось
• Радикальный центр
• Теорема о произведении отрезков хорд

Ссылки[править | править код]

• На Викискладе есть медиафайлы по теме Степень точки относительно окружности

Степень точки, формула

Степень точки — относительно окружности радиуса r называется величина:

[ d^2-r^2 ]

(d – расстояние от точки до центра окружности, r – радиус окружности)
Степень внешней точки — положительная, степень внутренней точки — отрицательная. Для точек окружности степень точки равна нулю.

Абсолютная величина степени точки обозначается так:

[ p^2 = lvert d^2-r^2 rvert ]

Если точка B — внешняя, то абсолютная величина степени точки есть квадрат длины касательной AB.

Если точка B — внутренняя, то степень точки равна квадрату наименьшей полухорды, проходящей через эту точку.

Зачем нужна степень точки? Практические задачи.

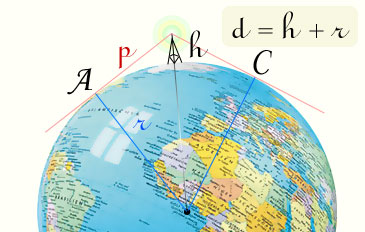
Практической задачей, где используется степень точки является например вычисление дальности вещания УКВ радиостанций. Известно, что радиоволны УКВ диапазона распространяются прямолинейно, как свет и прием возможен только в зоне прямой видимости. Таким образом зная высоту антенны и радиус Земли, вычислим степень точки и получим дальность вещания.
Взяв средний радиус Земли 6350 километров, высота антенны например 200 метров – после расчета получим дальность связи (степень точки) ≈ 50.4 километров.

Вычислить, найти степень точки по формуле (2)

Степень точки	стр. 241

Степень точки, формула

Степень точки — относительно окружности радиуса r называется величина:

(d – расстояние от точки до центра окружности, r – радиус окружности) Степень внешней точки — положительная, степень внутренней точки — отрицательная. Для точек окружности степень точки равна нулю.

Абсолютная величина степени точки обозначается так:

Если точка B — внешняя, то абсолютная величина степени точки есть квадрат длины касательной AB.

Если точка B — внутренняя, то степень точки равна квадрату наименьшей полухорды, проходящей через эту точку.

Зачем нужна степень точки? Практические задачи.

Практической задачей, где используется степень точки является например вычисление дальности вещания УКВ радиостанций. Известно, что радиоволны УКВ диапазона распространяются прямолинейно, как свет и прием возможен только в зоне прямой видимости. Таким образом зная высоту антенны и радиус Земли, вычислим степень точки и получим дальность вещания. Взяв средний радиус Земли 6350 километров, высота антенны например 200 метров – после расчета получим дальность связи (степень точки) ≈ 50.4 километров.

Что такое окружность: определение, свойства, формулы

В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.

Определение окружности

Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.

Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.

Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.

Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).

Свойства окружности

Свойство 1

Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.

Свойство 2

Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3

Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.

Формулы

1. Диаметр окружности (d):

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 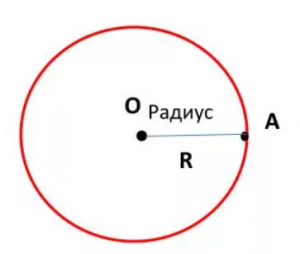Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

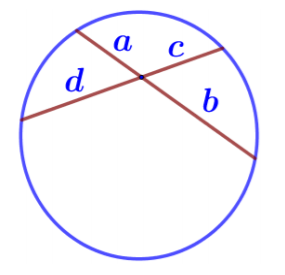
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Дуга, касательная, круг, сектор, сегмент

Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

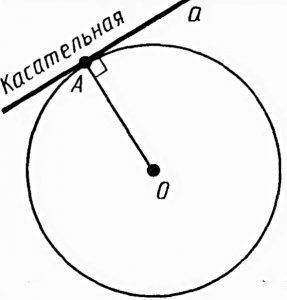
Свойства касательной

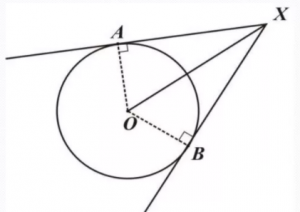
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

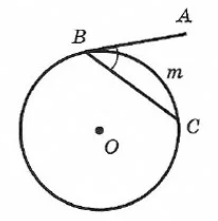
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

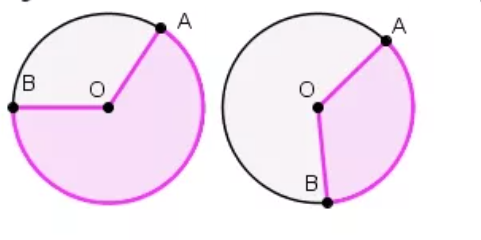
Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.

[spoiler title=”источники:”]

[/spoiler]

Определение. Величина δ=OK²-r² называется степенью точки K относительно окружности O(r).

Если δ>0, то точка К лежит вне окружности.

Если δ<0, то точка K лежит внутри окружности.

Если δ=0, то точка К лежит на окружности.

Теорема. Если две секущие пересекаются в точке K и одна из них пересекает окружность в точках A1 и A2, а другая пересекает окружность в точках B1 и B2, то 

KA₁·KA₂=KB₁·KB₂.

Таким образом произведение KA₁·KA₂ постоянно для данной окружности и данной точки K, т.е. не зависит от выбора секущей.

Следствие. Если секущая, проходящая через точку K, пересекает окружность O(r) в точках A₁ и A₂, то 

A₁K·A₂K=|OK²-r²|_.

Степень точки относительно окружности — это геометрическая величина, которая характеризует положение данной точки относительно определённой окружности на плоскости.

В геометрии степень произвольной точки P относительно окружности с центром в точке O можно вычислить по следующей формуле:

h = s^2 – r^2

где

h — степень точки P;

s — расстояние между точками P и O (длина отрезка PO);

r — радиус окружности.

Таким образом, величина h может быть положительной, отрицательной или равной нулю.

Степень точки, лежащей вне окружности, положительна.

Степень точки, лежащей внутри окружности, отрицательна.

Степень точки, лежащей на окружности (принадлежащей окружности), равна нулю.

На представленном рисунке: степень точки P положительна, точки O — отрицательна, точек A, B, M, N, T — равна нулю.

Аналогично степени точки относительно окружности в планиметрии, в стереометрии выделяют степень точки относительно сферы. Определение в данном случае существенно не меняется; степенью точки M относительно сферы с центром O называют вещественное число, равное OM^2 – R^2, где OM — длина отрезка OM, а R — радиус сферы. Степень точек, лежащих вне сферы, положительна; степень точек, лежащих внутри сферы, отрицательна, а степень точек, лежащих на сфере (то есть на поверхности шара), равна нулю.