Как найти степень в математике 5 класс

Математика

5 класс

Урок № 13

Степень с натуральным показателем

Перечень вопросов, рассматриваемых в теме:

– понятие степени с натуральным показателем;

– вычисление квадрата числа;

– вычисление куба числа.

Тезаурус

Степень числа а с натуральным показателем n (n > 1) – это произведение n натуральных множителей, каждый из которых равен а. Записывается aⁿ, а- основание степени, n- показатель.

Квадрат числа – это вторая степень числа.

Куб числа – это третья степень числа.

Обязательная литература

Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

Дополнительная литература

Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.

Теоретический материал для самостоятельного изучения

Нам известно, что сумму нескольких одинаковых слагаемых принято записывать короче – в виде произведения:

4 + 4 + 4 + 4 + 4 = 4 ∙ 5

Произведение одинаковых чисел также можно записать короче:

4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4⁵

Это произведение можно записать короче, полученный результат называют степенью. Читается так: «четыре в пятой степени».

Запись 4³ (четыре в степени три) означает 4 ∙ 4 ∙ 4. При этом число 4 называют основанием степени, а число 3 – показателем степени. Число три показывает, сколько раз нужно взять множителем основание степени – число 4: 4³= 4 ∙ 4 ∙ 4 = 64.

Степенью числа а с натуральным показателем n (n > 1) называют произведение n натуральных множителей, каждый из которых равен а:

Рассмотрим несколько примеров. Вычислим 2⁵, 2 в качестве множителя повторяется 5 раз, значит: 2⁵ = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32.

Теперь вычислим 3⁷. 3 в качестве множителя повторяется 7 раз, значит: 3⁷= 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 2187.

Таким образом, можно вычислить любую степень числа с натуральным показателем, большим единицы. Стоит запомнить, что любое число в первой степени будет ровняться ему самому, т. е. a¹= a.

Вторую степень числа называют квадратом числа. Запись 4² читают «четыре в квадрате». Третью степень числа называют кубом числа. Запись 4³ читают «четыре в кубе».

Обратите внимание на таблицы квадратов и кубов натуральных чисел. Со временем вы их запомните.

Разбор решения заданий тренировочного модуля

№ 1. Найдите чему равно 13⁴= ____.

Решение: чтобы узнать чему равно 13⁴, надо представить 13⁴ в виде произведения четырёх одинаковых множителей и выполнить умножение: 13⁴ = 13 ∙ 13∙ 13 ∙ 13 = 28561.

Ответ: 13⁴ = 28561

№ 2. Чему равна пятая степень 19? Выберите верный ответ.

247699
2476099
247609
2467099

Решение: чтобы вычислить 19⁵, надо представить 19⁵ в виде произведения пяти одинаковых множителей и выполнить умножение: 19⁵ = 19 ∙ 19∙ 19 ∙ 19 = 2476099.

Ответ: 2. 2476099

Источник

Главная
Справочники
Справочник по математике 5-9 класс
Натуральные числа и действия над ними
Степень числа. Квадрат и куб числа

Определение.

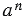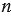Выражение “” читают так: “ в степени ” или “ 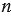– ая степень числа “, и называют степенью. При этом в этой записи число “” называют основанием степени, а число “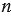“, которое показывает число множителей в произведении, – показателем степени.

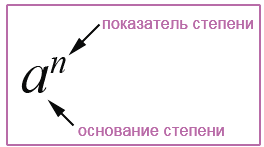
Например, найдем значение следующих степеней:

2⁴ = 2222 = 422 = 82 = 16;

3⁶ = 333333 = 93333 = 27333 = 8133 =2433 = 729.

Квадрат числа – это вторая степень числа. Квадрат числа записывают так: 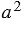. Читают: “ в квадрате” или “ во второй степени”.

Например, найдем квадрат чисел 4 и 8:

4² = 44 = 16;

8² = 88 = 64.

Куб числа – это третья степень числа. Куб числа записывают так: 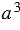. Читают: “ в кубе” или “ в третей степени”.

Например, найдем куб чисел 5 и 7:

5³ = 555 = 255 = 125;

7³ = 777 = 495 = 343;

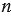Степенью числа “” с показателем = 1 является само это число, то есть .

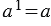Ноль в любой степени – это ноль, единица – это единица.

0ⁿ = 0;

1ⁿ = 1.

Действительно, т.к. степень можно расписать как произведение, то, если в основании находится ноль, то мы получим произведение n нолей, если единица – произведение n единиц.

Возведение числа в степень – это пятое арифметическое действие, поэтому стоит учитывать, что:

Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом – остальные действия, в соответствии с порядком их выполнения.

Например, найдем значение выражения 64² – (3 + 2):

Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:

64² – (3 + 2) = 616 – (3 + 2) = 616 – 5 = 96 – 5 = 91.

Советуем посмотреть:

Понятие о натуральном числе

Сложение натуральных чисел

Вычитание натуральных чисел

Умножение натуральных чисел

Деление натуральных чисел

Порядок выполнения действий

Меньше или больше

Меньше или больше на сколько? во сколько раз?

Формулы

Уравнения

Натуральные числа и действия над ними

Правило встречается в следующих упражнениях:

5 класс

Задание 657,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 666,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 667,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 693,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 730,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 813,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 824,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 659,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Номер 632,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 100,
Мерзляк, Полонский, Якир, Учебник

Номер 106,
Мерзляк, Полонский, Якир, Учебник

Номер 178,
Мерзляк, Полонский, Якир, Учебник

Номер 1046,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Задание 478,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 914,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 916,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1143,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Номер 64,
Мерзляк, Полонский, Якир, Учебник

Номер 135,
Мерзляк, Полонский, Якир, Учебник

Номер 145,
Мерзляк, Полонский, Якир, Учебник

Номер 564,
Мерзляк, Полонский, Якир, Учебник

Номер 770,
Мерзляк, Полонский, Якир, Учебник

Номер 1001,
Мерзляк, Полонский, Якир, Учебник

Номер 1003,
Мерзляк, Полонский, Якир, Учебник

Номер 1138,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 378,
Мерзляк, Полонский, Якир, Учебник

Номер 380,
Мерзляк, Полонский, Якир, Учебник

Номер 381,
Мерзляк, Полонский, Якир, Учебник

Номер 401,
Мерзляк, Полонский, Якир, Учебник

Номер 484,
Мерзляк, Полонский, Якир, Учебник

Номер 486,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 500,
Мерзляк, Полонский, Якир, Учебник

Номер 509,
Мерзляк, Полонский, Якир, Учебник

Номер 519,
Мерзляк, Полонский, Якир, Учебник

Источник

Степень числа

4.5

Средняя оценка: 4.5

Всего получено оценок: 215.

4.5

Средняя оценка: 4.5

Всего получено оценок: 215.

Степень – это еще один тема в изучении арифметических действий. Первой было сложение и вычитание, второй – умножение и деление, третьей станет возведение в степень и извлечение корня. Знание степеней и их свойств позволяет значительно ускорить счет, а зачастую без этих знаний не обойтись при решении уравнений математики 5 класса.

Определение

Что значит возвести в степень? Это значит умножить число само на себя какое-то количество раз. Какое именно – показывает показатель степени. Сама степень состоит из двух частей. Основание – это то число, которое мы будем умножать само на себя. Показатель – это число, показывающее сколько раз число нужно умножить само на себя. Вот и вся формула степени числа.

Понимание разных частей формулы степени обязательно. Поскольку без него будет трудно в дальнейшем понять, что же такое логарифм.

Например, ${2^3}$ – означает, что число 2 нужно умножить само на себя 3 раза.

$$2^3=2*2*2=8$$

Чаще всего возводится в квадрат, потому что числа в квадрате очень часто применяются в физических и математических вычислениях. Но и более высокие степени есть и нужно уметь их вычислять. Специально для квадратов и кубов составлены краткие таблицы, которые позволяют быстро вычислить то или иное значение степени, без вычислений по возведению.

Свойство степеней

У степени всего 6 свойств. Для каждого из них есть буквенная формулировка.

Если делятся степени с одинаковым основанием, то основание остается прежним, а степени вычитаются.

$$5^8 : 5^3=5^{8-3}=5^5$$

Если степень числа возводится в степень, то основание остается прежним, а степени числа перемножаются.

$$(5^8)^3=5^{8*3}=5^{24}$$

Если числа в скобке перемножаются, а сама скобка возводится в степень, то каждый множитель возводится в степень.

$$(5*11)^{14}=5^{14}*11^{14}$$

Если в степень возводится дробь, то в степень возводится числитель и знаменатель дроби.

$$({3over5})^7={3^7over5^7}$$

Отрицательный знак показателя означает, что в степень возводится дробь, знаменатель которой равен основанию степени, а числитель единице

$$3^{-5}=({1over3})^5={1over(3^5)}$$

Дробный показатель степени означает, что из основания нужно извлечь корень той же степени, что и знаменатель, и возвести в ту же степень, что и числитель.

$$3^{3over2}= sqrt{3^2}$$

Свойства это хороший вариант быстро подсчитать результат больших чисел. Найти число в степени не так трудно, особенно с современными калькуляторами и таблицами степеней. А вот понять, какое именно число и в какую степень возводить, это уже задача для человеческого ума.

Корень

Обратное действие для возведения в степень это извлечение корня. Извлечение корня подразумевает под собой необходимость узнать, какое число возводили в ту или иную степень, чтобы получилось искомое число.

Если мы ищем квадратный корень из 4, то необходимо узнать, какое натуральное число возводилось в квадрат для получения числа 4.

$$sqrt{4}=2$$

Заключение

Что мы узнали?

Мы дали определение степени числа, разобрали, как расписывается степень в выражениях. Определили 6 свойств степени, привели формулировку и буквенную запись для каждой из них. Поговорили об обратном для степени действии – корне, о его значении и способах вычисления.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Лаки Сахалина

4/5
Лада Суркова

5/5
Telefoshka Pushkina

4/5
Таня Фомченко

5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 215.

А какая ваша оценка?

Источник

Обращаем ваше внимание, что в данном разделе разбирается
понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями
(с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа.
Для записи произведения числа самого на себя несколько раз
применяют сокращённое обозначение.

Вместо
произведения шести одинаковых множителей
4 · 4 · 4 · 4 · 4 · 4 пишут
4⁶ и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

4 — основание степени;
⁶ — показатель степени.

$основание и показатель степени$

В общем виде степень с основанием «a» и
показателем «n» записывается с помощью выражения:

$определение степени в буквенном выражении$

Запомните!
$!$

Степенью числа «a» с натуральным показателем «n»,
бóльшим 1, называется произведение «n»
одинаковых множителей, каждый из которых равен числу
«a».

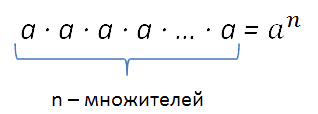
$что такое степень числа$

Запись «aⁿ» читается так:
«а в степени
n» или «n-ая степень числа
a».

Исключение составляют записи:

a² — её можно произносить как «а в квадрате»;
a³ — её можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

a² — «а во второй степени»;
a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

Запомните!
$!$

Степенью числа «а» с показателем n = 1 является само это число:
a¹ = a

Любое число в нулевой степени равно единице.
a⁰ = 1

Ноль в любой натуральной степени равен нулю.
0ⁿ = 0

Единица в любой степени равна 1.
1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишённым смысла.

(−32)⁰ = 1
0²⁵³ = 0
1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в
степень.

Пример. Возвести в степень.

5³ = 5 · 5 · 5 = 125
2,5² = 2,5 · 2,5 = 6,25
()⁴
=
·

·

·

=

3 · 3 · 3 · 3

4 · 4 · 4 · 4

=

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым
числом — положительным, отрицательным или нулём.

Запомните!
$!$

При возведении в степень положительного числа
получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться
как положительное число, так и отрицательное число. Это зависит от того чётным или
нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

$разные примеры возведения в степень отрицательных чисел$

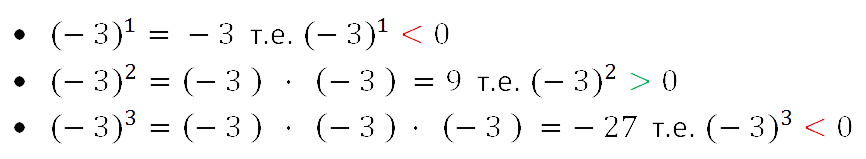
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень,
то получается отрицательное число. Так как произведение
нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число.
Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!
$!$

Отрицательное число, возведённое в
чётную степень, есть число
положительное.

Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

2 · (−3)² = 2 · (−3) · (−3) = 2 · 9 = 18
−5 · (−2)³ = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи
(−5)⁴ и
−5⁴ это разные выражения. Результаты возведения
в степень данных выражений будут разные.

Вычислить (−5)⁴ означает найти значение четвёртой степени отрицательного числа.

(−5)⁴ = (−5) · (−5) · (−5) · (−5) = 625

В то время как найти «−5⁴» означает, что пример нужно решать в 2 действия:

Возвести в четвёртую степень положительное число 5.

5⁴ = 5 · 5 · 5 · 5 = 625
Поставить перед полученным результатом знак «минус» (то есть выполнить
действие вычитание).

−5⁴ = −625

Пример. Вычислить: −6² − (−1)⁴

−6² − (−1)⁴ = −37

6² = 6 · 6 = 36
−6² = −36
(−1)⁴ = (−1) · (−1) · (−1) · (−1) = 1
−(−1)⁴ = −1
−36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните!
$!$

В выражениях со степенями, не содержащими скобки, сначала выполняют
вовзведение в степень, затем умножение и деление, а в
конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках,
а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

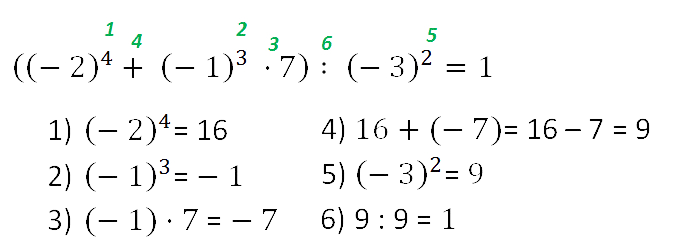
$пример порядка действийсо степенями$

Для облегчения решения примеров полезно знать и пользоваться
таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором
«Возведение в степень онлайн».

Ваши комментарии

Важно!
$Галка$

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

$Пришелец пожимает плечами$

Оставить комментарий:

14 апреля 2020 в 14:01

Bmw Touring
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Bmw Touring
Профиль
Благодарили: 0

Сообщений: 1

Скажите пожалуйста почему или как получился такой ответ?
Как именно получилось 10⁴ ?
0,4 · 10^{5 =}4 · 10^{4
спасибо за внимание!}

0
Спасибо $thanks$
Ответить

3 мая 2020 в 20:38
Ответ для Bmw Touring

Денис Волков
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Денис Волков
Профиль
Благодарили: 0

Сообщений: 3

0.4 · 10⁵ = 0.4 · 10 · 10⁴=(0.4 · 10 ) · 10⁴=4 · 10⁴

0
Спасибо $thanks$
Ответить

5 марта 2017 в 17:00

Виктория Горловская
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Виктория Горловская
Профиль
Благодарили: 0

Сообщений: 2

помогите пожалуйста
нужно правило что такое степень с натуральным показателем

0
Спасибо $thanks$
Ответить

5 марта 2017 в 18:22
Ответ для Виктория Горловская

Виктория Горловская
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Виктория Горловская
Профиль
Благодарили: 0

Сообщений: 2

$cry$

0
Спасибо $thanks$
Ответить

7 марта 2017 в 20:29
Ответ для Виктория Горловская

Валерий Шакиров
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Валерий Шакиров
Профиль
Благодарили: 0

Сообщений: 1

Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a. Степенью числа a споказателем 1 называется само число a (a¹ = a).. Степенью ненулевого числа a с показателем 0 равна единице (a⁰ = 1).

0
Спасибо $thanks$
Ответить

7 декабря 2016 в 8:58

Мирослава Заруцкая
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Мирослава Заруцкая
Профиль
Благодарили: 0

Сообщений: 3

мне не понятны степени как их упрощать $cry$ 2³^·2^{4 можно с объяснением}

0
Спасибо $thanks$
Ответить

7 декабря 2016 в 9:01
Ответ для Мирослава Заруцкая

Мирослава Заруцкая
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Мирослава Заруцкая
Профиль
Благодарили: 0

Сообщений: 3

СРОЧНО ОТВЕТЬТЕ ПОЖАЛУЙТА

0
Спасибо $thanks$
Ответить

7 декабря 2016 в 9:03
Ответ для Мирослава Заруцкая

Мирослава Заруцкая
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Мирослава Заруцкая
Профиль
Благодарили: 0

Сообщений: 3

ПОЖАЛУЙСТАААА

0
Спасибо $thanks$
Ответить

7 декабря 2016 в 12:12
Ответ для Мирослава Заруцкая

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

А учебник открыть лень?

0
Спасибо $thanks$
Ответить

20 ноября 2016 в 22:14

Злата Крамаренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Злата Крамаренко
Профиль
Благодарили: 0

Сообщений: 3

2x²+ 2y² — 2xy + 1 — 2y = 1/3

0
Спасибо $thanks$
Ответить

21 ноября 2016 в 4:21
Ответ для Злата Крамаренко

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

x = 1/3; y = 2/3.

0
Спасибо $thanks$
Ответить

21 ноября 2016 в 22:31
Ответ для Злата Крамаренко

Злата Крамаренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Злата Крамаренко
Профиль
Благодарили: 0

Сообщений: 3

Спасибо. А как разложить данное уравнение? Можно узнать, пожалуйста?

0
Спасибо $thanks$
Ответить

22 ноября 2016 в 1:12
Ответ для Злата Крамаренко

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

Сверни квадраты
+ = 0.

0
Спасибо $thanks$
Ответить

1 марта 2016 в 10:42

Екатерина Гулиева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Екатерина Гулиева
Профиль
Благодарили: 0

Сообщений: 1

какое число больше 7

в 3 раза, какое число меньше 7

в 3 раза

0
Спасибо $thanks$
Ответить

1 марта 2016 в 14:12
Ответ для Екатерина Гулиева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Если число больше в 3 раза, это значит, что текущее число, надо умножить на 3, а если меньше в 3 раза-разделить.
1) 7 ·3= ·3==21
Ответ : 21 в 3 раза больше, чем 7
2)7 : 3 = : 3 = = =2 =2
Ответ: 2 в 3 раза меньше, чем 7

0
Спасибо $thanks$
Ответить

27 декабря 2015 в 19:36

Надежда Егина
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Надежда Егина
Профиль
Благодарили: 0

Сообщений: 2

5^{6 ·}125 : 25⁴

0
Спасибо $thanks$
Ответить

10 января 2016 в 1:43
Ответ для Надежда Егина

Татьяна Почтарёва
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Татьяна Почтарёва
Профиль
Благодарили: 0

Сообщений: 2

5⁶·5³:5⁸=5¹=5

0
Спасибо $thanks$
Ответить

25 октября 2015 в 10:21

Валерия Соколова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Валерия Соколова
Профиль
Благодарили: 0

Сообщений: 1

((?2)^?2)^?2

0
Спасибо $thanks$
Ответить

12 июня 2016 в 2:47
Ответ для Валерия Соколова

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

0
Спасибо $thanks$
Ответить

16 октября 2015 в 18:02

Влада Данилова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Влада Данилова
Профиль
Благодарили: 0

Сообщений: 1

Представьте в виде степени с основание 4 число 16

0
Спасибо $thanks$
Ответить

17 октября 2015 в 0:14
Ответ для Влада Данилова

Людмила Кундина
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Людмила Кундина
Профиль
Благодарили: 0

Сообщений: 1

4²

0
Спасибо $thanks$
Ответить

7 октября 2015 в 18:02

Елена Облупина
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Елена Облупина
Профиль
Благодарили: 0

Сообщений: 1

Число 9 возвели в степень 5, полученный результат возвели в степень2. В какую степень за два раза возвели число 9????

0
Спасибо $thanks$
Ответить

12 сентября 2016 в 16:02
Ответ для Елена Облупина

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

(9⁵)²=9¹⁰При возведении степени в степень, степени перемножаются. Свойство №3

0
Спасибо $thanks$
Ответить

16 сентября 2015 в 15:45

Евгений Куринной
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Евгений Куринной
Профиль
Благодарили: 0

Сообщений: 4

Помогите пожалуйста решить: корень 4 степени из дроби: в числителе 81, в знаменателе 16

0
Спасибо $thanks$
Ответить

16 сентября 2015 в 15:54
Ответ для Евгений Куринной

Евгений Куринной
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Евгений Куринной
Профиль
Благодарили: 0

Сообщений: 4

Это я уже решил, помогите решить этот: корень 8 степени из 16 в -4 степени

0
Спасибо $thanks$
Ответить

16 сентября 2015 в 16:00
Ответ для Евгений Куринной

Евгений Куринной
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Евгений Куринной
Профиль
Благодарили: 0

Сообщений: 4

Уже решил

0
Спасибо $thanks$
Ответить

5 сентября 2016 в 14:24
Ответ для Евгений Куринной

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Отличная ветка математического форума ) Так держать! =) Если будет необходимо, подробнее о действиях со степенями можно прочесть здесь: http://math-prosto.ru/index.php?page=pages/stepeni/stepeni2.php

0
Спасибо $thanks$
Ответить

Источник

Эта информация доступна зарегистрированным пользователям

На данном уроке мы познакомимся с понятием степени числа.

Выясним, что называют «показателем степени» и «основанием степени».

Научимся вычислять квадрат и куб числа.

Составим таблицу степеней первых десяти натуральных чисел и рассмотрим ряд задач с использованием таких таблиц.

Определим, в каком порядке выполняют действия в выражениях, содержащих степень.

Эта информация доступна зарегистрированным пользователям

Известно, что сумму равных слагаемых можно заменить произведением.

Например, сумму пяти слагаемых, каждое из которых равняется четырем, можно записать короче:

4 + 4 + 4 + 4 + 4 = 5 ∙ 4

В произведении число 5 указывает на количество одинаковых слагаемых.

В свою очередь произведение одинаковых множителей тоже можно записать компактнее.

Эта информация доступна зарегистрированным пользователям

Произведение n одинаковых множителей можно представить в виде степени.

В буквенном виде произведение равных множителей можно представить следующим образом:

Эта информация доступна зарегистрированным пользователям

аⁿ– это произведение числа а на само себя n раз.

а– любое натуральное число.

Читают «а в n-ной степени» или «а в степени n».

Число а называют основанием (число, возводимое в степень).

n– это показатель степени (число, которое указывает сколько раз повторяется основание степени).

Степень числа представляют всегда так: записывают основание степени, а показатель ее записывают меньше размером в верхнем правом углу основания степени.

Операция умножения одинаковых множителей называется возведением в степень.

Например, произведение пяти множителей, каждое из которых равняется четырем, можно записать так:

4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4⁵

Читают данную запись следующим образом:

4⁵– четыре в пятой степени.

Пример:

1)Вычислим значение степени 2³, т.е. возведем число два в третью степень.

Данная степень равна произведению трех двоек.

Эта информация доступна зарегистрированным пользователям

2– основание степени.

3– показатель степени.

2) Вычислим значение степени 5⁴, т.е. возведем число пять в четвертую степень.

Данная степень равна произведению четырех пятерок.

Эта информация доступна зарегистрированным пользователям

5– основание степени.

4– показатель степени.

Эта информация доступна зарегистрированным пользователям

Вторую степень числа называют квадратом числа.

Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а² (говорят и читают «а в квадрате»).

Эта информация доступна зарегистрированным пользователям

Например,

2² (два во второй степени) иначе говорят и читают «два в квадрате».

10² (десять во второй степени) иначе говорят и читают «десять в квадрате».

27² (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».

Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.

Один в квадрате равняется одному: 1² = 1 ∙ 1 = 1.

Два в квадрате равняется четырем: 2² = 2 ∙ 2 = 4.

Три в квадрате равняется девяти: 3² = 3 ∙ 3 = 9.

Четыре в квадрате равняется шестнадцати: 4² = 4 ∙ 4 = 16.

Пять в квадрате равняется двадцати пяти: 5² = 5 ∙ 5 = 25.

Шесть в квадрате равняется тридцати шести: 6² = 6 ∙ 6 = 36.

Семь в квадрате равняется сорока девяти: 7² = 7 ∙ 7 = 49.

Восемь в квадрате равняется шестидесяти четырем: 8² = 8 ∙ 8 = 64.

Девять в квадрате равняется восьмидесяти одному: 9² = 9 ∙ 9 = 81.

Десять в квадрате равняется сотне: 10² = 10 ∙ 10 = 100.

Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.

Таблица квадратов первых десяти натуральных чисел
а	1	2	3	4	5	6	7	8	9	10
а²	1	4	9	16	25	36	49	64	81	100

Пример.

Учитывая данные таблицы квадратов, решим уравнение.

Решим уравнение х² = 49.

Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).

По таблице квадратов видно, что 49 = 7².

Следовательно, корень уравнения (х) равен семи.

х² = 49

х = 7

Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х² = 49, получим:

7² = 49

7 ∙ 7 = 49

49 = 49

Ответ: х = 7.

Эта информация доступна зарегистрированным пользователям

Третья степень числа тоже имеет свое название.

Число в третьей степени называют кубом числа.

Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а³ (говорят и читают «а в кубе»).

Эта информация доступна зарегистрированным пользователям

Например,

2³ (два в третьей степени) иначе говорят и читают «два в кубе».

10³ (десять в третьей степени) иначе говорят и читают «десять в кубе».

27³ (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».

Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.

Один в кубе: 1³ = 1 ∙ 1 ∙ 1 = 1.

Два в кубе: 2³ = 2 ∙ 2 ∙ 2 = 8.

Три в кубе: 3³ = 3 ∙ 3 ∙ 3 = 27.

Четыре в кубе: 4³ = 4 ∙ 4 ∙ 4 = 64.

Пять в кубе: 5³ = 5 ∙ 5 ∙ 5 = 125.

Шесть в кубе: 6³ = 6 ∙ 6 ∙ 6 = 216.

Семь в кубе: 7³ = 7 ∙ 7 ∙ 7 = 343.

Восемь в кубе: 8³ = 8 ∙ 8 ∙ 8 = 512.

Девять в кубе: 9³ = 9 ∙ 9 ∙ 9 = 729.

Десять в кубе: 10³ = 10 ∙ 10 ∙ 10 = 1000.

Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.

Таблица кубов первых десяти натуральных чисел
а	1	2	3	4	5	6	7	8	9	10
а³	1	8	27	64	125	216	343	512	729	1000

С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.

Пример.

Представим в виде куба число 343.

По таблице кубов видим, что 343 = 7³

Проверим: найдем произведение трех семерок:

7³ = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343

Ответ: 343 = 7³.

На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.

Эта информация доступна зарегистрированным пользователям

Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.

Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.

Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.

За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.

Рассмотрим поясняющие примеры.

При решении различных задач и примеров будем пользоваться составленными таблицами степеней.

Пример 1.

Найдите значение выражения 8² ÷ 4 – 10.

Определим порядок действий в выражении и найдем его значение.

Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).

8² ÷ 4 – 10 = 6

1) 8² = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).

2) 64 ÷ 4 = 16

3) 16 – 10 = 6

Пример 2.

Найдите значение выражения (21 – 11)² ∙ 2³.

Найдем значение данного выражения, определив порядок действий в нем.

(21 – 11)² ∙ 2³ = 800

Согласно порядка выполнения действий сначала выполняются действия в скобках.

Найдем разность 21 и 11.

1) 21 – 11 = 10

Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.

Найдем, чему равно 10² по определению степени или по таблице квадратов.

2) 10² = 10 ∙ 10 = 100

Затем выполним действия, которые находятся в исходном выражении за скобками.

Определим третью степень двойки по таблице кубов или по определению степеней.

3) 2³ = 2 ∙ 2 ∙ 2 = 8

Далее перемножим результаты, полученные в во втором и в третьем действии соответственно, т.е. найдем произведение 100 и 8.

4) 100 ∙ 8 = 800

Эта информация доступна зарегистрированным пользователям

Степень обладает рядом свойств, которые подробно вы будете рассматривать и доказывать в старших классах.

Эта информация доступна зарегистрированным пользователям

Сейчас мы познакомимся с некоторыми особенными свойствами степеней.

1. Любое число в первой степени равно этому же числу.

Первая степень числа а равна числу а.

В буквенном виде данное свойство запишем так:

а¹ = а

Данная запись означает, что основание степени необходимо взять в качестве множителя один раз.

Например,

5¹ = 5, 127¹ = 127, 1004¹ = 1004, 123456¹ = 123456 и т.д.

Соответственно и единица в первой степени всегда равна единице: 1¹ = 1.

2. Любое натуральное число в нулевой степени равно единице.

а⁰ = 1

Например,

5⁰ = 1, 127⁰ = 1, 10⁰ = 1, 123456⁰ = 1 и т.д.

3. Ноль в любой степени равен нулю: 0ⁿ = 0.

На самом деле, по известному нам определению степени, 0 является основанием, n– показатель степени, указывающий сколько раз повторяется основание степени.

Таким образом получаем следующее равенство:

Эта информация доступна зарегистрированным пользователям

Например,

Эта информация доступна зарегистрированным пользователям

0¹²⁸ = 0

0¹⁵⁰⁰⁰ = 0

Слово «степень», порой, встречается в вашей повседневной жизни.

Степенные выражения используют в различных областях знаний, в науке и технике.

Часто приходится при расчетах и измерении встречаться с очень большими и очень маленькими числами.

С такими числами неудобно работать: выполнять различные действия и вычисления.

Иногда числа удобно представить в виде степени, записывая их, например, в стандартном виде.

Стандартный вид числа обобщенно можно записать так:

а ∙ 10ⁿ

В данной записи число (а), которое умножается на 10 в какой-либо степени, должно быть больше единицы или равно ей и быть меньше десяти.

Пример.

200000 = 2 ∙ 10⁵

8000000000000 = 8 ∙ 10¹²

500 = 5 ∙ 10²

Однозначное число, записанное в стандартном виде, будет равно самому себе, умноженному на десять в нулевой степени.

а = а ∙ 10⁰ = а ∙ 1 = а

Пример.

2 = 2 ∙ 10⁰ = 2 ∙ 1 = 2

5 = 5 ∙ 10⁰ = 5 ∙ 1 = 5

8 = 8 ∙ 10⁰ = 8 ∙ 1 = 8

Число десять представляют в стандартном виде, как произведение единицы и 10 в первой степени.

10 = 1 ∙ 10¹ = 1 ∙ 10 = 10

Изучая разряды и классы чисел, мы только лишь упоминали о больших и гигантских числах.

Известно, например, что один миллион записывается как единица и шесть нулей после нее.

Эта информация доступна зарегистрированным пользователям

В стандартном виде миллион запишем так:

1000000 = 1 ∙ 10⁶.

Миллиард записывается следующим образом: единица и девять нулей после нее.

Эта информация доступна зарегистрированным пользователям

В стандартном виде миллиард запишем так:

1000000000 = 1 ∙ 10⁹

Триллион представляет собой единицу и двенадцать нулей после нее.

Эта информация доступна зарегистрированным пользователям

В стандартном виде триллион запишем так:

1000000000000 = 1 ∙ 10¹².

Самое большое число, которое называется «гугол», в десятичной системе исчисления изображается в виде единицы со ста нулями, записывают 10¹⁰⁰ (десять в степени сто).

Часто при решение различных задач удобно записывать числа сокращенно, с помощью степеней.

Пример.

24000 = 24 ∙ 10³

350000 = 35 ∙ 10⁴

24500000 = 245 ∙ 10⁵

Однако, при этом эти числа не будут относится к числам, записанным в стандартном виде, так как 24 > 10, 35 > 10, 245 > 10.

Данные числа всего лишь имеют компактный вид, удобный при вычислениях.

Эта информация доступна зарегистрированным пользователям

Квадратом числа называют произведение двух одинаковых множителей.

Мы уже пробовали находить квадраты первого десятка натуральных чисел.

Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.

Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.

1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.

2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).

3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).

4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.

Рассмотрим поясняющий пример.

Найдем квадрат 65.

65² = 65 ∙ 65

Первая цифра в числе 65– это цифра 6, следовательно, нам необходимо найти произведение 6 и суммы 6 + 1.

6 ∙ (6 + 1) = 6 ∙ 7 = 42

Запишем число 42 и припишем к нему число 25.

65² = 4225

Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65² = 65 ∙ 65, то

65² = 65 ∙ 65 = 4225

Получили все тот же ответ: 65² = 4225

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Степень числа

Определение

Свойство степеней

Корень

Что мы узнали?

Тест по теме

Оценка статьи

Возведение в степень отрицательного числа

Обратите внимание!

Порядок действий в примерах со степенями

Ваши комментарии

Читайте также

Добавить комментарий Отменить ответ

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Степень числа

Определение

Свойство степеней

Корень

Что мы узнали?

Тест по теме

Оценка статьи

Возведение в степень отрицательного числа

Обратите внимание!

Порядок действий в примерах со степенями

Ваши комментарии

Читайте также

Вам также может понравиться

Как найти менеджер файлов на телефоне

Как найти средний квадрат индивидуальных значений

Как найти проекцию наклонной зная наклонную

Добавить комментарий Отменить ответ