Как найти степень в уравнении с дробями

Как решать
показательные уравнения?

Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.

Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:

Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:

Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.

И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:

И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.

Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.

Простейшие показательные уравнения

Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:

Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:

Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.

Решим что-нибудь посложнее.

Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:

Мы применили свойство отрицательной степени по формуле:

Теперь наше уравнение будет выглядеть так:

Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:

Такое мы решать умеем, ведь это обыкновенное линейное уравнение.

Поздравляю, мы нашли корень нашего показательного уравнения.

Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:

Воспользуемся одним из свойств степеней ((a^n)^m=a^):

И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:

И еще один пример:

Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.

Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.

Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.

Общий метод решения показательных уравнений

Пусть у нас есть вот такой пример:

Где (a,b) какие-то положительные числа. ((a>0, ; b>0).

Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.

Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:

Раз основания одинаковые, то мы можем просто приравнять степени:

Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:

Замечаем, что (16=2*2*2*2=2^4) это степень двойки:

Основания одинаковые, значит можно приравнять степени:

$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$

Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).

Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:

(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):

Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):

Подставим данное преобразование в наш пример:

Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:

Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.

Кто забыл, что такое логарифм, можно посмотреть здесь.

Рассмотрим еще несколько аналогичных примеров.

Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:

Все эти варианты ответа верные, их можно смело писать в ответ.

И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).

Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:

Решение показательных уравнений при помощи замены

Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.

Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:

Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.

Квадратное уравнение, которое решается через дискриминант:

Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:

И второй корень:

И еще один пример на замену:

Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):

Подставим в исходное уравнение:

Теперь показательные функции одинаковы и можно сделать замену:

Обратная замена, и наше уравнение сводится к простейшему:

И второе значение (t):

Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):

Здесь нам придется воспользоваться свойствами степеней:

Разберем каждое слагаемое:

Теперь подставим получившееся преобразования в исходное уравнение:

Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):

Сделаем обратную замену:

И последний пример на замену:

Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:

Разберем каждое слагаемое нашего уравнения:

Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!

И последнее слагаемое со степенью:

Подставим все наши преобразования в исходное уравнение:

Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):

Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.

И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут

Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:

Воспользуемся формулой ((a*b)^n=a^n*b^n):

И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:

Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):

Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.

Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!

Показательные уравнения

О чем эта статья:

6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.

Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

Степень уравнения

Кроме разделения уравнений по количеству неизвестных, уравнения также разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.

Чтобы определить степень уравнения, в нём нужно предварительно сделать следующие преобразования:

• раскрыть скобки,
• освободить уравнение от дробных членов,
• перенести все неизвестные члены в одну из частей уравнения,
• сделать приведение подобных членов.

После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:

Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.

10 — x = 2 — уравнение первой степени с одним неизвестным;

x 2 + 7x = 16 — уравнение второй степени с одним неизвестным;

x 3 = 8 — уравнение третьей степени с одним неизвестным.

Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.

Для примера возьмём уравнение

Для наглядности расставим показатели первой степени (которые обычно не ставят):

3x 2 y 1 + x 1 y 1 + 25 1 = 0.

Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:

3x 2 y 1 — сумма показателей равна 2 + 1 = 3;

x 1 y 1 — сумма показателей равна 1 + 1 = 2.

Сумма показателей у первого члена уравнения больше, чем у второго, значит, при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит, что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.

2xy — x = 25 — уравнение второй степени с двумя неизвестным,

xy 2 — 2xy + 8y = 0 — уравнение третьей степени с двумя неизвестными.

Содержание:

Рациональные уравнения. Равносильные уравнения

Напомним что:

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения – не равносильны, так как корнем первого уравнения является число 10, а корнем второго – число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Рассмотрим уравнения:

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения – дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и – целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, – единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Ответ. 3.

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

х – 1 х – 2

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Ответ. 4.

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 – единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

1) найти ОДЗ переменной в уравнении; & 2) найти простейший общий знаменатель дробей, входящий в уравнение;

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе – два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Ответ. Нет.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где – натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями – это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Пример №206

Замените степень дробью:

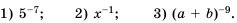
Решение:

По определению:

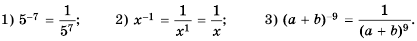
Пример №207

Замените дробь степенью с целым отрицательным показателем:

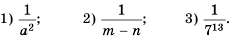
Решение:

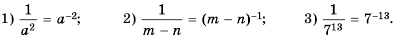
Пример №208

Вычислите: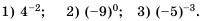

Решение:

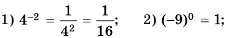
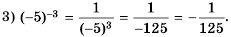
Рассмотрим, как возвести дробь 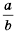в целую отрицательную степень. Если 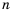– натуральное число и 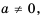имеем:

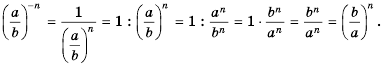
Следовательно,

Если 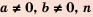– натуральное число, то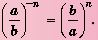

Пример №209

Найдите значение выражения:

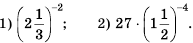
Решение:

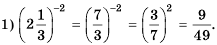
2) Учитывая порядок выполнения арифметических действий, сначала возведем дробь в степень, а затем выполним умножение:

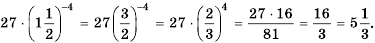
Ответ.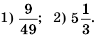

Свойства степени с целым показателем

Свойства степени с натуральным показателем справедливы и для степени с ненулевым основанием и целым показателем. Следовательно,

Для любого 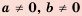любых целых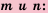

Эти свойства можно доказать на основании формулы 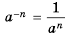и свойств степени с натуральным показателем.

Докажем, например, формулу 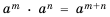для случая, когда 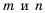отрицательные целые числа.

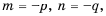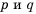Пусть где натуральные числа. Имеем:

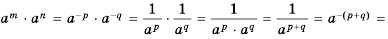
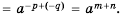
Следовательно, 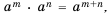где 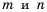– отрицательные целые числа. В случае, когда один из показателе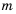й или 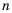-целое отрицательное число, а второй – натуральное число или нуль, формула доказывается аналогично.

Пример №210

Выполните действие:

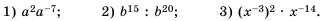
Решение:

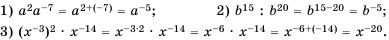
Пример №211

Упростите выражение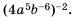

Решение:

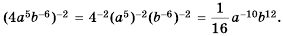
Пример №212

Вычислите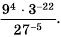

Решение:

Представим 9 и 27 в виде степени с основанием 3 и воспользуемся свойствами степени:

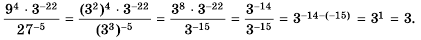
Ответ. 3.

Стандартный вид числа

В физике, химии, технике, астрономии часто имеют дело как с очень большими, так и с очень малыми значениями величин. Например, масса Земли равна 5 976 ООО ООО ООО ООО ООО ООО ООО кг, а диаметр молекулы водорода 0,00000000025 м.

Читать или записывать такие числа в виде десятичных дробей неудобно, неудобно и использовать десятичную их запись при вычислениях. В таких случаях имеет смысл записывать число в ви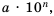де где 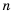– целое число,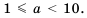

Например,

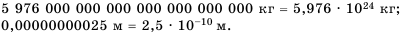
Говорят, что числа 5 976 000 000 000 000 000 000 000 и 0,00000000025 записаны в стандартном виде.

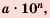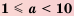Стандартным видом числа называют его запись в виде произведении где и 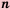— целое число.

Если число записано в стандартном виде, то показатель степени 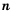называют порядком числа. Например, порядок числа, которым записана масса Земли в килограммах, равен 24, а порядок числа, которым записан диаметр молекулы водорода в метрах, равен -10.

В стандартном виде можно записать любое положительное число. Порядок числа дает представление об этом числе.

Если порядок числа 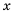равен 4, это значит, что 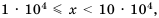то есть 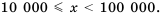Если порядок числа 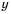равен -2, то 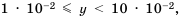то есть 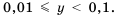Большой положительный порядок числа показывает, что число очень большое. Большой по модулю отрицательный порядок числа показывает, что число очень маленькое.

Следовательно, если говорят, что одно число на порядок больше второго, это означает, что оно в 10 раз больше второго, если на два порядка – в 100 раз больше и т. д.

Пример №213

Представьте число 272 000 в стандартном виде.

Решение:

В данном числе поставим занятую так, чтобы в целой части была одна цифра, отличная от нуля. В итоге будем иметь 2,72. Занятой отделили 5 цифр с конца числа, чем уменьшили данное число в 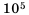раз. Следовательно,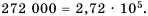

Ответ.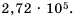

Пример №214

Представьте число 0,00013 в стандартном виде.

Решение:

В данном числе перенесем запятую на 4 знака вправо, будем иметь 1,3. При этом число увеличили в 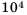раз (на 4 порядка). Следовательно,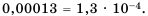

Ответ.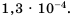

Пример №215

Выполните действия и представьте результат в стандартном виде:

Решение:

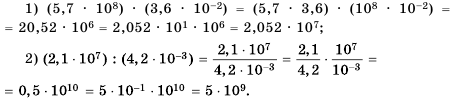
Ответ.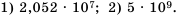

Пример №216

Найдите сумму 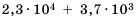и запишите результат в стандартном виде.

Решение:

Имеем два слагаемых разных порядков.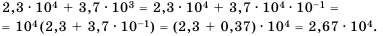

Ответ.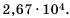

Функция Y=K/X ее график и свойства

Функция 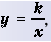ее график и свойства

Пример №217

Пешеход должен преодолеть путь в 16 км. Если он будет двигаться со скоростью 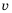км/ч, то зависимость времени 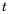(в часах) для преодоления этого расстояния от скорости движения можно выразить формулой 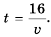При увеличении значения 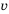в несколько раз значение 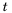во столько же раз уменьшится. В этом случае говорят, что переменные 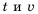обратно пропорциональны.

Пример №218

Площадь прямоугольника равна 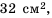а одна из его сторон 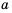см. Тогда вторую сторону 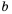(в см) можно найти по формуле 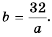Здесь переменные 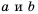также обратно пропорциональны.

В примерах 1 и 2 переменные 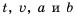принимают только положительные значения. В дальнейшем будем рассматривать функции, которые задают формулой вида 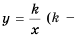число, 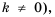где переменные 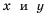могут принимать как положительные, так и отрицательные значения. Каждую из таких функций называют обратной пропорциональностью.

Функцию вида 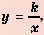где 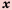— независимая неременная, 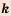– некоторое отличное от нуля число, называют обратной пропорциональностью.

Область определения функции 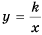все числа за исключением нуля, так как при 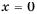выражение не имеет смысла.

Построим график функции 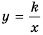отдельно для каждого из случаев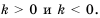

Пример №219

Постройте график функции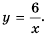

Решение:

Составим таблицу значений функции 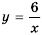для нескольких значений аргумента:

Отметим на координатной плоскости точки из составленной таблицы (рис. 2).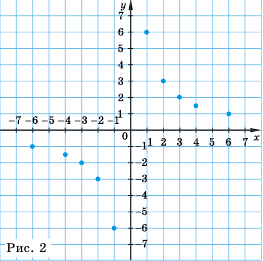

Если бы мы на этой плоскости обозначили больше точек, удовлетворяющих формуле 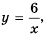а потом соединили их плавной линией, то получили бы график функции 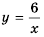(рис. 3).

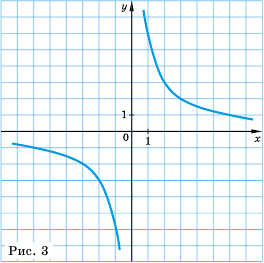
График обратной пропорциональности называют гиперболой.

Гипербола состоит из двух ветвей. Для функции 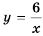одна из них лежит в первой координатной четверти, а другая – в третьей. Гипербола не пересекает координатные оси: график не содержит точек, у которых 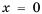(т. к. нуль не принадлежит области определения функции), и не содержит точек, у которых

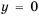(т. к. уравнение 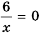не имеет решений). Чем больше по модулю значение 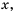тем меньше по модулю значение 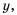и наоборот, чем меньше по модулю значение 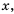тем больше по модулю значение 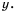Это значит, что ветви гиперболы неограниченно приближаются к осям координат.

Так же выглядит график функции 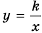при любом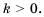

Пример №220

Постройте график функции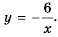

Решение:

Рассуждая как и в предыдущем примере, построим график функции 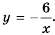Он изображен на рисунке 4.

Это также гипербола, одна из ветвей которой лежит во второй координатной четверти, а другая – в четвертой.

Так же выглядит график функции 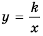при любом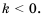

Обобщим свойства обратной пропорциональности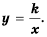

1. Область определения функции состоит из всех чисел за исключением нуля.

2. Область значений функции состоит из всех чисел за исключением нуля.

3. График функции – гипербола, ветви которой при лежат в первой и третьей координатных четвертях, а при – во второй и четвертой.

4. Ветви гиперболы неограниченно приближаются к осям координат.

Пример №221

Постройте в одной системе координат графики функций 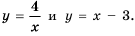Найдите их точки пересечения и, пользуясь построенным графиком, решите уравнение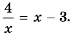

Решение:

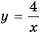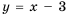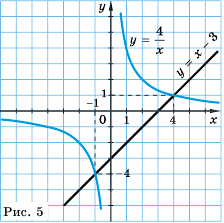
График функции гипербола, ветви которой лежат в первой и третьей координатных четвертях, а график функции прямая, проходящая через точки 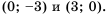Графики функций изображены на рисунке 5. Они пересекаются в точках 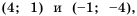абсциссы 4 и -1 которых являются решениями уравнения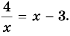

Действительно, при 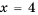выражения 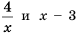принимают

равные значения: 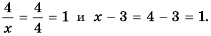При 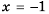аналогично: 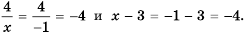Следовательно, числа 4 и -1 – корни уравнения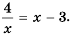

Ответ: 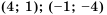– точки пересечения; 4, -1 – корни уравнения.

Предложенный в примере 5 метод решения уравнений называют графическим методом решения уравнений.

Если абсцисса точки пересечения графиков функций – целое число, надо выполнить проверку, т. к. часто корни уравнения этим методом можно найти только приблизительно.

Пример №222

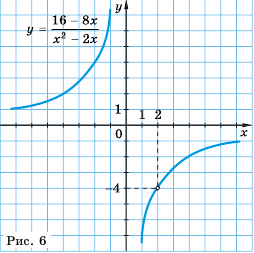
Постройте график функции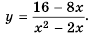

Решение:

Область определения функции – все числа за исключением чисел 0 и 2, которые обращают знаменатель в нуль.

Упростим дробь: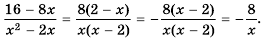

Значит при условии 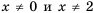функция принимает вид 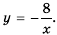Графиком функции 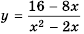является гипербола 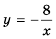с «выколотой» точкой 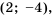точек же с абсциссой 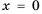у гиперболы нет (рис. 6).

————

Если все решения одного уравнения также являются решениями второго, то второе уравнение называется следствием первого уравнения.

Если множества решений двух уравнений совпадают, то эти уравнения называются равносильными.

Пример 1.

Равносильны ли уравнения?

Решение:

1) Оба уравнения имеют общий корень: х=1. Так как они не имеют других корней, то они являются равносильными.

2) Первое уравнение имеет корень, равный 0. Второе же уравнение такого корня не имеет. Значит, данные уравнения не равносильны.

Пусть Р(х) и Q(x) – многочлены переменной х.

Выражение вида 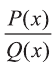называется рациональным.

Пусть А(х) и В(х) – рациональные выражения. Уравнение вида А(х)=В(х) называется рациональным.

Рассмотрим сначала простейшее рациональное уравнение вида

Известно, что дробь 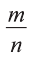равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля (на нуль делить нельзя!). Значит, для того, чтобы решить уравнение (1) , необходимо и достаточно найти все значения неизвестной х, для которых одновременно выполнены условия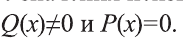

Для краткости, это мы будем записывать так: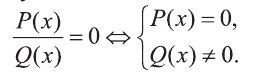

• Заказать решение задач по высшей математике

Пример:

Решите уравнение:

Решение:

Уравнение 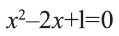имеет единственное решение х=1. При х=1 знаменатель отличен от нуля. Значит, данное уравнение тоже имеет единственное решение х=1.

2) Квадратное уравнение 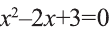не имеет корней, так как 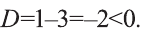Значит, данное уравнение тоже не имеет корней.

3) Для квадратного уравнения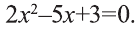

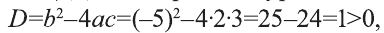Значит, это уравнение имеет два корня:

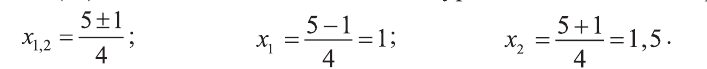
Однако число 1,5 обращает знаменатель выражения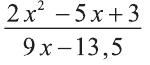

в нуль, а число 1 – нет. Значит, данное уравнение имеет единственное решение х=1.

4) Уравнение 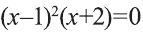имеет два корня 1 и-2. Однако число 1 обращает знаменатель (х-1) в нуль, а число -2 – нет. Значит, данное уравнение имеет единственное решение х=—2.

В случае, когда хотя бы одно из выражений А(х) и В(х) представимо в виде суммы нескольких рациональных выражений, рациональное уравнение А(х)=В(х) можно решить так:

• 1 шаг. Ищем общий знаменатель дробей, входящих в уравнение;
• 2 шаг. Обе части уравнения умножаем на этот общий знаменатель;
• 3 шаг. Ищем решения полученного уравнения;
• 4 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель в нуль.

Пример:

Решите уравнение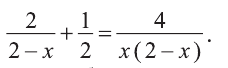

Решение:

Умножаем обе части уравнения на общий знаменатель 2х(2-х). Упрощая полученное уравнение 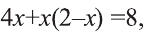, приводим его к следующему квадратному уравнению: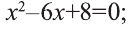

Так как D=9-8=l>0, то данное квадратное уравнение имеет два корня:

х=2; х=4.

Проверка.

При х=2 знаменатель обращается в нуль: х(2-х) = 2(2-2) = 0. Значит, х=2

не является решением исходного уравнения.

При х=4 знаменатель отличен от нуля х(2-х) = 4(2-4) Ф 0. Значит, х=4

является решением исходного уравнения.

Если 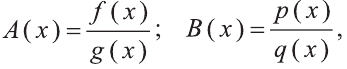то при решении рационального уравнения вида 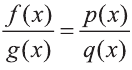полезно воспользоваться основным свойством пропорции: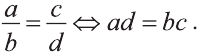

При этом получим следующий алгоритм решения:

• 1 шаг. Ищем решения уравнения f (х)q(х) = р(х)g(х)
• 2 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель q(x)g(x) в нуль.

Пример:

Решите уравнение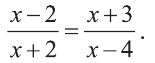

Решение:

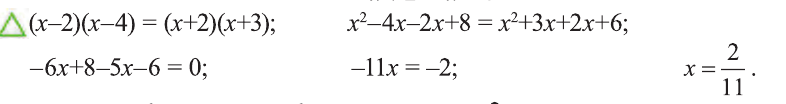
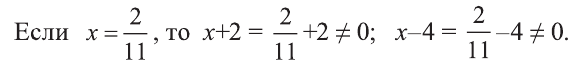
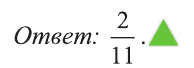
В некоторых случаях удачно выполненная замена позволяет привести заданное уравнение к более простому.

Пример:

Решите уравнение:

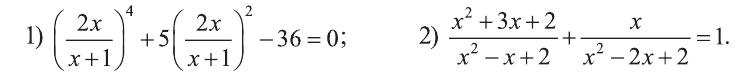
Решение:

 1) Выполним замену 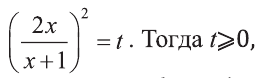а уравнение получит вид 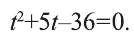Последнее имеет корни t=-9 и t=4, из которых второе положительно.

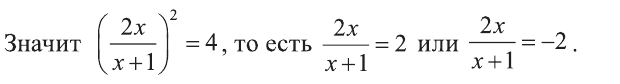
При 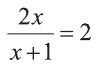уравнение не имеет решение, а при 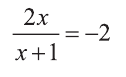уравнение имеет единственное решение х=-0,5.

Ответ: х=-0,5. 

2) Очевидно, что х=0 удовлетворяет уравнению. Пусть 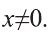. Разделив в каждой дроби уравнения числитель и знаменатель на х, получим уравнение

Тогда наше уравнение получит вид: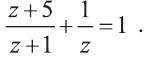

Решим последнее уравнение:

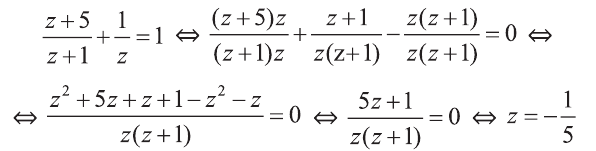
Теперь найдем x.

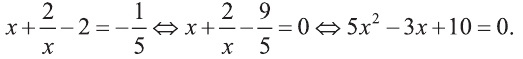
В силу того, что дискриминант квадратного уравнения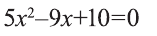 отрицателен, то последнее уравнение не имеет действительных решений. Ответ: х=0.

Системы рациональных уравнений

Решение систем, состоящих из рациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует не забывать, что знаменатели, участвующих рациональных выражений, не могут обращаться в нуль.

Пример:

Решите систему:

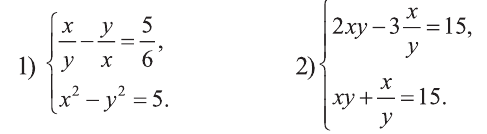
Решение:

1) Сделаем в первом уравнении замену 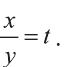Получим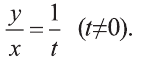

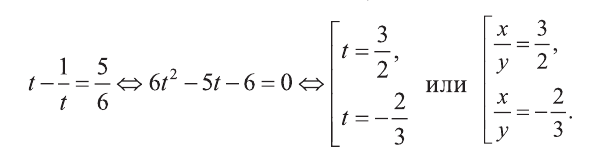
Отсюда или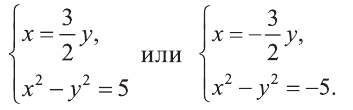

Решим полученные системы: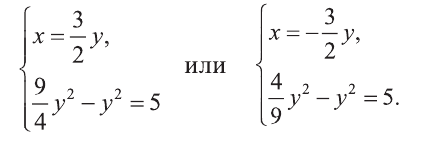

Первая система имеет решения (3,2), (-3, -2), а вторая не имеет решений. Ответ: (3; 2), (-3; -2).

2). Обозначим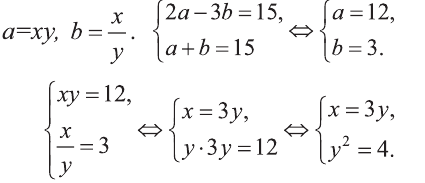

——

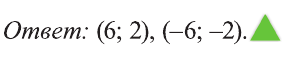
Рациональные уравнения

Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.

Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.

Это интересно!

На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.

Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.

Рациональные уравнения

Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).

Пример:

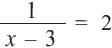В данном уравнении ОДЗ 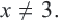Учитывая, что 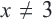умножим обе части уравнения на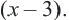

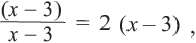отсюда получим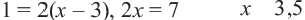

Подставим полученное значение в уравнение: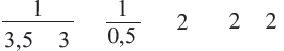

Таким образом, 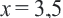является корнем уравнения. Данное уравнение не имеет других корней.

Пример:

Решим уравнение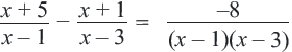

ОДЗ данного уравнения 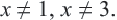Умножим обе части уравнения на общий

знаменатель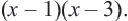

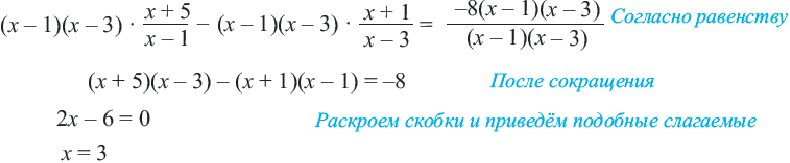
Пример:

В уравнении, 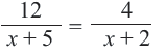ОДЗ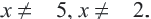

Используя свойство пропорции можно написать: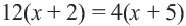

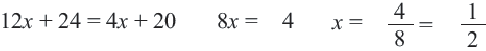
Пример:

Решим уравнение. 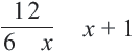Здесь ОДЗ,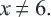

Умножим обе части уравнения на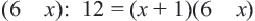

Отсюда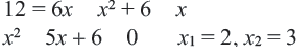

Проверьте, являются ли оба этих числа корнями данного уравнения.

Пример:

Решим уравнение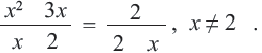

Запишем уравнение в виде 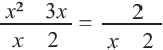и умножим обе стороны на общий множитель 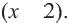Получим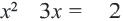

Отсюда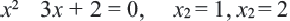

При проверке, убеждаемся что, 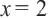не удовлетворяет уравнению, т.к. превращает знаменатель в «0». Таким образом, корнем данного уравнения является только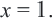

Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней.

Решение задач с помощью рациональных уравнений

Задачи на работу

Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за 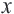дней, тогда 1-ый рабочий выполнит её за 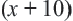дней

Первый рабочий за 1 день выполняет 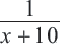– ую часть работы, 2-ой – 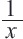– ую. Вместе, за 1 день они выполнят 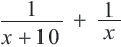часть работы. Зная, что вместе за 1 день они выполняют 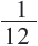часть работы (согласно условию), составим уравнение 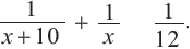Умножим обе части уравнения на 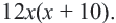Получим, 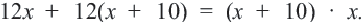После упрощения имеем Решением данного уравнения являются числа и 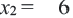(не удовлетворяет условию, т.к. ). Итак 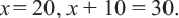Ответ: 2-ой рабочий выполняет работу за 20 дней, а 1-ый – за 30 дней.

Задачи на движение

Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.

1-й способ:

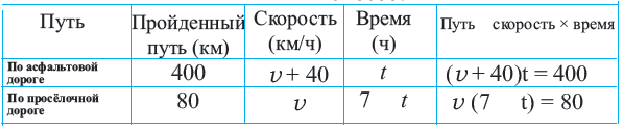Из 2-ой строки таблицы: 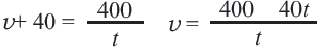Из 3-е1 строки таблицы: 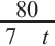Отсюда получаем рациональное уравнение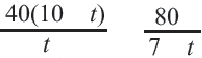

Разделим обе части уравнения на 40: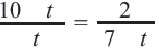

Получим 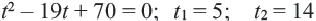(противоречит условию задачи)

Ответ: по просёлочной дороге 2 часа

2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом 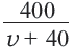часов, а по проселочной дороге 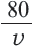часов.

Зная, что на весь путь он потратил 7 часов, составим уравнение: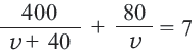

Решив данное уравнение, получим 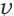= 40 км/ч. Тогда по просёлочной дороге он двигался 80 : 40 = 2 часа.

Что такое показательное уравнение и как его решать

20 декабря 2016

Этот урок предназначен для тех, кто только начинает изучать показательные уравнения. Как всегда, начнём с определения и простейших примеров.

Если вы читаете этот урок, то я подозреваю, что вы уже имеете хотя бы минимальное представление о простейших уравнениях — линейных и квадратных: $56x-11=0$; ${{x}^{2}}+5x+4=0$; ${{x}^{2}}-12x+32=0$ и т.д. Уметь решать такие конструкции совершенно необходимо для того, чтобы не «зависнуть» в той теме, о которой сейчас пойдёт речь.

Итак, показательные уравнения. Сразу приведу парочку примеров:

[{{2}^{x}}=4;quad {{5}^{2x-3}}=frac{1}{25};quad {{9}^{x}}=-3]

Какие-то из них могут показаться вам более сложными, какие-то — напротив, слишком простыми. Но всех их объединяет один важный признак: в их записи присутствует показательная функция $fleft( x right)={{a}^{x}}$. Таким образом, введём определение:

Показательное уравнение — это любое уравнение, содержащее в себе показательную функцию, т.е. выражение вида ${{a}^{x}}$. Помимо указанной функции подобные уравнения могут содержать в себе любые другие алгебраические конструкции — многочлены, корни, тригонометрию, логарифмы и т.д.

Ну хорошо. С определением разобрались. Теперь вопрос: как всю эту хрень решать? Ответ одновременно и прост, и сложен.

Начнём с хорошей новости: по своему опыту занятий с множеством учеников могу сказать, что большинству из них показательные уравнения даются намного легче, чем те же логарифмы и уж тем более тригонометрия.

Но есть и плохая новость: иногда составителей задач для всевозможных учебников и экзаменов посещает «вдохновение», и их воспалённый наркотиками мозг начинает выдавать такие зверские уравнения, что решить их становится проблематично не только ученикам — даже многие учителя на таких задачах залипают.

Впрочем, не будем о грустном. И вернёмся к тем трём уравнениям, которые были приведены в самом начале повествования. Попробуем решить каждое из них.

Первое уравнение: ${{2}^{x}}=4$. Ну и в какую степень надо возвести число 2, чтобы получить число 4? Наверное, во вторую? Ведь ${{2}^{2}}=2cdot 2=4$ — и мы получили верное числовое равенство, т.е. действительно $x=2$. Что ж, спасибо, кэп, но это уравнение было настолько простым, что его решил бы даже мой кот.:)

Посмотрим на следующее уравнение:

[{{5}^{2x-3}}=frac{1}{25}]

А вот тут уже чуть сложнее. Многие ученики знают, что ${{5}^{2}}=25$ — это таблица умножения. Некоторые также подозревают, что ${{5}^{-1}}=frac{1}{5}$ — это по сути определение отрицательных степеней (по аналогии с формулой ${{a}^{-n}}=frac{1}{{{a}^{n}}}$).

Наконец, лишь избранные догадываются, что эти факты можно совмещать и на выходе получить следующий результат:

[frac{1}{25}=frac{1}{{{5}^{2}}}={{5}^{-2}}]

Таким образом, наше исходное уравнение перепишется следующим образом:

[{{5}^{2x-3}}=frac{1}{25}Rightarrow {{5}^{2x-3}}={{5}^{-2}}]

А вот это уже вполне решаемо! Слева в уравнении стоит показательная функция, справа в уравнении стоит показательная функция, ничего кроме них нигде больше нет. Следовательно, можно «отбросить» основания и тупо приравнять показатели:

[2x-3=-2]

Получили простейшее линейное уравнение, которое любой ученик решит буквально в пару строчек. Ну ладно, в четыре строчки:

[begin{align}& 2x-3=-2 \& 2x=3-2 \& 2x=1 \& x=frac{1}{2} \end{align}]

Если вы не поняли, что сейчас происходило в последних четырёх строчках — обязательно вернитесь в тему «линейные уравнения» и повторите её. Потому что без чёткого усвоения этой темы вам рано браться за показательные уравнения.

Со всеми остальными мы идём дальше. На очереди третье уравнение:

[{{9}^{x}}=-3]

Ну и как такое решать? Первая мысль: $9=3cdot 3={{3}^{2}}$, поэтому исходное уравнение можно переписать так:

[{{left( {{3}^{2}} right)}^{x}}=-3]

Затем вспоминаем, что при возведении степени в степень показатели перемножаются:

[{{left( {{3}^{2}} right)}^{x}}={{3}^{2x}}Rightarrow {{3}^{2x}}=-{{3}^{1}}]

Ну а дальше вообще всё стандартно:

[begin{align}& 2x=-1 \& x=-frac{1}{2} \end{align}]

И вот за такое решение мы получим честно заслуженную двойку. Ибо мы с невозмутимостью покемона отправили знак «минус», стоящий перед тройкой, в степень этой самой тройки. А так делать нельзя. И вот почему. Взгляните на разные степени тройки:

[begin{matrix} {{3}^{1}}=3& {{3}^{-1}}=frac{1}{3}& {{3}^{frac{1}{2}}}=sqrt{3} \ {{3}^{2}}=9& {{3}^{-2}}=frac{1}{9}& {{3}^{frac{1}{3}}}=sqrt[3]{3} \ {{3}^{3}}=27& {{3}^{-3}}=frac{1}{27}& {{3}^{-frac{1}{2}}}=frac{1}{sqrt{3}} \end{matrix}]

Составляя эту табличку, я уж как только не извращался: и положительные степени рассмотрел, и отрицательные, и даже дробные… ну и где здесь хоть одно отрицательное число? Его нет! И не может быть, потому что показательная функция $y={{a}^{x}}$, во-первых, всегда принимает лишь положительные значения (сколько единицу не умножай или не дели на двойку — всё равно будет положительное число), а во-вторых, основание такой функции — число $a$ — по определению является положительным числом!

Ну и как тогда решать уравнение ${{9}^{x}}=-3$? А никак: корней нет. И в этом смысле показательные уравнения очень похожи на квадратные — там тоже может не быть корней. Но если в квадратных уравнениях число корней определяется дискриминантом (дискриминант положительный — 2 корня, отрицательный — нет корней), то в показательных всё зависит от того, что стоит справа от знака равенства.

Таким образом, сформулируем ключевой вывод: простейшее показательное уравнение вида ${{a}^{x}}=b$ имеет корень тогда и только тогда, когда $b gt 0$. Зная этот простой факт, вы без труда определите: есть у предложенного вам уравнения корни или нет. Т.е. стоит ли вообще его решать или сразу записать, что корней нет.

Это знание ещё неоднократно поможет нам, когда придётся решать более сложные задачи. А пока хватит лирики — пора изучить основной алгоритм решения показательных уравнений.

Как решать показательные уравнения

Итак, сформулируем задачу. Необходимо решить показательное уравнение:

[{{a}^{x}}=b,quad a,b gt 0]

Согласно «наивному» алгоритму, по которому мы действовали ранее, необходимо представить число $b$ как степень числа $a$:

[b={{a}^{m}}Rightarrow {{a}^{x}}={{a}^{m}}Rightarrow x=m]

Кроме того, если вместо переменной $x$ будет стоять какое-либо выражение, мы получим новое уравнение, которое уже вполне можно решить. Например:

[begin{align}& {{2}^{x}}=8Rightarrow {{2}^{x}}={{2}^{3}}Rightarrow x=3; \& {{3}^{-x}}=81Rightarrow {{3}^{-x}}={{3}^{4}}Rightarrow -x=4Rightarrow x=-4; \& {{5}^{2x}}=125Rightarrow {{5}^{2x}}={{5}^{3}}Rightarrow 2x=3Rightarrow x=frac{3}{2}. \end{align}]

И как ни странно, эта схема работает примерно в 90% случаев. А что тогда с остальными 10%? Остальные 10% — это немного «шизофреничные» показательные уравнения вида:

[{{2}^{x}}=3;quad {{5}^{x}}=15;quad {{4}^{2x}}=11]

Ну и в какую степень надо возвести 2, чтобы получить 3? В первую? А вот и нет: ${{2}^{1}}=2$ — маловато. Во вторую? Тоже нет: ${{2}^{2}}=4$ — многовато. А в какую тогда?

Знающие ученики уже наверняка догадались: в таких случаях, когда «красиво» решить не получается, к делу подключается «тяжёлая артиллерия» — логарифмы. Напомню, что с помощью логарифмов любое положительное число можно представить как степень любого другого положительного числа (за исключением единицы):

[a={{b}^{{{log }_{b}}a}},quad a gt 0,quad 1ne b gt 0]

Помните эту формулу? Когда я рассказываю своим ученикам про логарифмы, то всегда предупреждаю: эта формула (она же — основное логарифмическое тождество или, если угодно, определение логарифма) будет преследовать вас её очень долго и «всплывать» в самых неожиданных местах. Ну вот она и всплыла. Давайте посмотрим на наше уравнение и на эту формулу:

[begin{align}& {{2}^{x}}=3 \& a={{b}^{{{log }_{b}}a}} \end{align}]

Если допустить, что $a=3$ — наше исходное число, стоящее справа, а $b=2$ — то самое основание показательной функции, к которому мы так хотим привести правую часть, то получим следующее:

[begin{align}& a={{b}^{{{log }_{b}}a}}Rightarrow 3={{2}^{{{log }_{2}}3}}; \& {{2}^{x}}=3Rightarrow {{2}^{x}}={{2}^{{{log }_{2}}3}}Rightarrow x={{log }_{2}}3. \end{align}]

Получили немного странный ответ: $x={{log }_{2}}3$. В каком-нибудь другом задании многие при таком ответе засомневались бы и начали перепроверять своё решение: вдруг там где-то закралась ошибка? Спешу вас обрадовать: никакой ошибки здесь нет, и логарифмы в корнях показательных уравнений — вполне типичная ситуация. Так что привыкайте.:)

Теперь решим по аналогии оставшиеся два уравнения:

[begin{align}& {{5}^{x}}=15Rightarrow {{5}^{x}}={{5}^{{{log }_{5}}15}}Rightarrow x={{log }_{5}}15; \& {{4}^{2x}}=11Rightarrow {{4}^{2x}}={{4}^{{{log }_{4}}11}}Rightarrow 2x={{log }_{4}}11Rightarrow x=frac{1}{2}{{log }_{4}}11. \end{align}]

Вот и всё! Кстати, последний ответ можно записать иначе:

[x=frac{1}{2}{{log }_{4}}11={{log }_{4}}{{11}^{frac{1}{2}}}={{log }_{4}}sqrt{11}]

Это мы внесли множитель в аргумент логарифма. Но никто не мешает нам внести этот множитель в основание:

[x=frac{1}{2}{{log }_{4}}11={{log }_{{{4}^{2}}}}11={{log }_{16}}11]

При этом все три варианта являются правильными — это просто разные формы записи одного и того же числа. Какой из них выбрать и записать в настоящем решении — решать только вам.

Таким образом, мы научились решать любые показательные уравнения вида ${{a}^{x}}=b$, где числа $a$ и $b$ строго положительны. Однако суровая реальность нашего мира такова, что подобные простые задачи будут встречаться вам очень и очень редко. Куда чаще вам будет попадаться что-нибудь типа этого:

[begin{align}& {{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11; \& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& {{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09. \end{align}]

Ну и как такое решать? Это вообще можно решить? И если да, то как?

Без паники. Все эти уравнения быстро и просто сводятся к тем простым формулам, которые мы уже рассмотрели. Нужно лишь знать вспомнить парочку приёмов из курса алгебры. Ну и конечно, здесь никуда без правил работы со степенями. Обо всём этом я сейчас расскажу.:)

Преобразование показательных уравнений

Первое, что нужно запомнить: любое показательное уравнение, каким бы сложным оно ни было, так или иначе должно сводиться к простейшим уравнениям — тем самым, которые мы уже рассмотрели и которые знаем как решать. Другими словами, схема решения любого показательного уравнения выглядит следующим образом:

1. Записать исходное уравнение. Например: ${{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11$;
2. Сделать какую-то непонятную хрень. Или даже несколько хреней, которые называются «преобразовать уравнение»;
3. На выходе получить простейшие выражения вида ${{4}^{x}}=4$ или что-нибудь ещё в таком духе. Причём одно исходное уравнение может давать сразу несколько таких выражений.

С первым пунктом всё понятно — записать уравнение на листик сможет даже мой кот. С третьим пунктом тоже, вроде, более-менее ясно — мы такие уравнения уже целую пачку нарешали выше.

Но как быть со вторым пунктом? Что за преобразования? Что во что преобразовывать? И как?

Что ж, давайте разбираться. Прежде всего, отмечу следующее. Все показательные уравнения делятся на два типа:

1. Уравнение составлено из показательных функций с одним и тем же основанием. Пример: ${{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11$;
2. В формуле присутствуют показательные функции с разными основаниями. Примеры: ${{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}$ и ${{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09$.

Начнём с уравнений первого типа — они решаются проще всего. И в их решении нам поможет такой приём как выделение устойчивых выражений.

Выделение устойчивого выражения

Давайте ещё раз посмотрим на это уравнение:

[{{4}^{x}}+{{4}^{x-1}}={{4}^{x+1}}-11]

Что мы видим? Четвёрка возводится в разные степени. Но все эти степени — простые суммы переменной $x$ с другими числами. Поэтому необходимо вспомнить правила работы со степенями:

[begin{align}& {{a}^{x+y}}={{a}^{x}}cdot {{a}^{y}}; \& {{a}^{x-y}}={{a}^{x}}:{{a}^{y}}=frac{{{a}^{x}}}{{{a}^{y}}}. \end{align}]

Проще говоря, сложение показателей можно преобразовать в произведение степеней, а вычитание легко преобразуется в деление. Попробуем применить эти формулы к степеням из нашего уравнения:

[begin{align}& {{4}^{x-1}}=frac{{{4}^{x}}}{{{4}^{1}}}={{4}^{x}}cdot frac{1}{4}; \& {{4}^{x+1}}={{4}^{x}}cdot {{4}^{1}}={{4}^{x}}cdot 4. \end{align}]

Перепишем исходное уравнение с учётом этого факта, а затем соберём все слагаемые слева:

[begin{align}& {{4}^{x}}+{{4}^{x}}cdot frac{1}{4}={{4}^{x}}cdot 4-11; \& {{4}^{x}}+{{4}^{x}}cdot frac{1}{4}-{{4}^{x}}cdot 4+11=0. \end{align}]

В первых четырёх слагаемых присутствует элемент ${{4}^{x}}$ — вынесем его за скобку:

[begin{align}& {{4}^{x}}cdot left( 1+frac{1}{4}-4 right)+11=0; \& {{4}^{x}}cdot frac{4+1-16}{4}+11=0; \& {{4}^{x}}cdot left( -frac{11}{4} right)=-11. \end{align}]

Осталось разделить обе части уравнения на дробь $-frac{11}{4}$, т.е. по существу умножить на перевёрнутую дробь — $-frac{4}{11}$. Получим:

[begin{align}& {{4}^{x}}cdot left( -frac{11}{4} right)cdot left( -frac{4}{11} right)=-11cdot left( -frac{4}{11} right); \& {{4}^{x}}=4; \& {{4}^{x}}={{4}^{1}}; \& x=1. \end{align}]

Вот и всё! Мы свели исходное уравнение к простейшему и получили окончательный ответ.

При этом в процессе решения мы обнаружили (и даже вынесли за скобку) общий множитель ${{4}^{x}}$ — это и есть устойчивое выражение. Его можно обозначать за новую переменную, а можно просто аккуратно выразить и получить ответ. В любом случае, ключевой принцип решения следующий:

Найти в исходном уравнении устойчивое выражение, содержащее переменную, которое легко выделяется из всех показательных функций.

Хорошая новость состоит в том, что практически каждое показательное уравнение допускает выделение такого устойчивого выражения.

Но есть и плохая новость: подобные выражения могут оказаться весьма хитрыми, и выделить их бывает довольно сложно. Поэтому разберём ещё одну задачу:

[{{5}^{x+2}}+{{0,2}^{-x-1}}+4cdot {{5}^{x+1}}=2]

Возможно, у кого-то сейчас возникнет вопрос: «Паша, ты что, обкурился? Здесь же разные основания — 5 и 0,2». Но давайте попробуем преобразовать степень с основание 0,2. Например, избавимся от десятичной дроби, приведя её к обычной:

[{{0,2}^{-x-1}}={{0,2}^{-left( x+1 right)}}={{left( frac{2}{10} right)}^{-left( x+1 right)}}={{left( frac{1}{5} right)}^{-left( x+1 right)}}]

Как видите, число 5 всё-таки появилось, пускай и в знаменателе. Заодно переписали показатель в виде отрицательного. А теперь вспоминаем одно из важнейших правил работы со степенями:

[{{a}^{-n}}=frac{1}{{{a}^{n}}}Rightarrow {{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( frac{5}{1} right)}^{x+1}}={{5}^{x+1}}]

Тут я, конечно, немного слукавил. Потому что для полного понимания формулу избавления от отрицательных показателей надо было записать так:

[{{a}^{-n}}=frac{1}{{{a}^{n}}}={{left( frac{1}{a} right)}^{n}}Rightarrow {{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( frac{5}{1} right)}^{x+1}}={{5}^{x+1}}]

С другой стороны, ничто не мешало нам работать с одной лишь дробью:

[{{left( frac{1}{5} right)}^{-left( x+1 right)}}={{left( {{5}^{-1}} right)}^{-left( x+1 right)}}={{5}^{left( -1 right)cdot left( -left( x+1 right) right)}}={{5}^{x+1}}]

Но в этом случае нужно уметь возводить степень в другую степень (напомню: при этом показатели складываются). Зато не пришлось «переворачивать» дроби — возможно, для кого-то это будет проще.:)

В любом случае, исходное показательное уравнение будет переписано в виде:

[begin{align}& {{5}^{x+2}}+{{5}^{x+1}}+4cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+5cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+{{5}^{1}}cdot {{5}^{x+1}}=2; \& {{5}^{x+2}}+{{5}^{x+2}}=2; \& 2cdot {{5}^{x+2}}=2; \& {{5}^{x+2}}=1. \end{align}]

Вот и получается, что исходное уравнение решается даже проще, чем ранее рассмотренное: тут даже не надо выделять устойчивое выражение — всё само сократилось. Осталось лишь вспомнить, что $1={{5}^{0}}$, откуда получим:

[begin{align}& {{5}^{x+2}}={{5}^{0}}; \& x+2=0; \& x=-2. \end{align}]

Вот и всё решение! Мы получили окончательный ответ: $x=-2$. При этом хотелось бы отметить один приём, который значительно упростил нам все выкладки:

В показательных уравнениях обязательно избавляйтесь от десятичных дробей, переводите их в обычные. Это позволит увидеть одинаковые основания степеней и значительно упростит решение.

Перейдём теперь к более сложным уравнениям, в которых присутствуют разные основания, которые вообще не сводятся друг к другу с помощью степеней.

Использование свойства степеней

Напомню, что у нас есть ещё два особо суровых уравнения:

[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& {{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09. \end{align}]

Основная сложность тут — непонятно, что и к какому основанию приводить. Где устойчивые выражения? Где одинаковые основания? Ничего этого нет.

Но попробуем пойти другим путём. Если нет готовых одинаковых оснований, их можно попробовать найти, раскладывая имеющиеся основания на множители.

Начнём с первого уравнения:

[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{21}^{3x}}; \& 21=7cdot 3Rightarrow {{21}^{3x}}={{left( 7cdot 3 right)}^{3x}}={{7}^{3x}}cdot {{3}^{3x}}. \end{align}]

Но ведь можно поступить наоборот — составить из чисел 7 и 3 число 21. Особенно это просто сделать слева, поскольку показатели и обеих степеней одинаковые:

[begin{align}& {{7}^{x+6}}cdot {{3}^{x+6}}={{left( 7cdot 3 right)}^{x+6}}={{21}^{x+6}}; \& {{21}^{x+6}}={{21}^{3x}}; \& x+6=3x; \& 2x=6; \& x=3. \end{align}]

Вот и всё! Вы вынесли показатель степени за пределы произведения и сразу получили красивое уравнение, которое решается в пару строчек.

Теперь разберёмся со вторым уравнением. Тут всё намного сложнее:

[{{100}^{x-1}}cdot {{2,7}^{1-x}}=0,09]

Прежде всего, сделаем то, что я рекомендовал ещё в самом начале урока — избавимся от десятичной дроби:

[{{100}^{x-1}}cdot {{left( frac{27}{10} right)}^{1-x}}=frac{9}{100}]

В данном случае дроби получились несократимыми, но если бы что-то можно было сократить — обязательно сокращайте. Зачастую при этом появятся интересные основания, с которыми уже можно работать.

У нас же, к сожалению, ничего особо не появилось. Зато мы видим, что показатели степеней, стоящий в произведении слева, противоположны:

[1-x=-left( x-1 right)Rightarrow {{left( frac{27}{10} right)}^{1-x}}={{left( frac{27}{10} right)}^{-left( x-1 right)}}={{left( frac{10}{27} right)}^{x-1}}]

Напомню: чтобы избавиться от знака «минус» в показателе, достаточно просто «перевернуть» дробь. Что ж, перепишем исходное уравнение:

[begin{align}& {{100}^{x-1}}cdot {{left( frac{10}{27} right)}^{x-1}}=frac{9}{100}; \& {{left( 100cdot frac{10}{27} right)}^{x-1}}=frac{9}{100}; \& {{left( frac{1000}{27} right)}^{x-1}}=frac{9}{100}. \end{align}]

Во второй строчке мы просто вынесли общий показатель из произведения за скобку по правилу ${{a}^{x}}cdot {{b}^{x}}={{left( acdot b right)}^{x}}$, а в последней просто умножили число 100 на дробь.

Теперь заметим, что числа, стоящие слева (в основании) и справа, чем-то похожи. Чем? Да очевидно же: они являются степенями одного и того же числа! Имеем:

[begin{align}& frac{1000}{27}=frac{{{10}^{3}}}{{{3}^{3}}}={{left( frac{10}{3} right)}^{3}}; \& frac{9}{100}=frac{{{3}^{2}}}{{{10}^{3}}}={{left( frac{3}{10} right)}^{2}}. \end{align}]

Таким образом, наше уравнение перепишется следующим образом:

[{{left( {{left( frac{10}{3} right)}^{3}} right)}^{x-1}}={{left( frac{3}{10} right)}^{2}}]

Дальше всё просто. При возведении степени в степень показатели перемножаются:

[{{left( {{left( frac{10}{3} right)}^{3}} right)}^{x-1}}={{left( frac{10}{3} right)}^{3left( x-1 right)}}={{left( frac{10}{3} right)}^{3x-3}}]

При этом справа тоже можно получить степень с таким же основанием, для чего достаточно просто «перевернуть» дробь:

[{{left( frac{3}{10} right)}^{2}}={{left( frac{10}{3} right)}^{-2}}]

Окончательно наше уравнение примет вид:

[begin{align}& {{left( frac{10}{3} right)}^{3x-3}}={{left( frac{10}{3} right)}^{-2}}; \& 3x-3=-2; \& 3x=1; \& x=frac{1}{3}. \end{align}]

Вот и всё решение. Основная его идея сводится к тому, что даже при разных основаниях мы пытаемся любыми правдами и неправдами свести эти основания к одному и тому же. В этом нам помогают элементарные преобразования уравнений и правила работы со степенями.

Но какие правила и когда использовать? Как понять, что в одном уравнении нужно делить обе стороны на что-то, а в другом — раскладывать основание показательной функции на множители?

Ответ на этот вопрос придёт с опытом. Попробуйте свои силы сначала на простых уравнениях, а затем постепенно усложняйте задачи — и очень скоро ваших навыков будет достаточно, чтобы решить любое показательное уравнение из того же ЕГЭ или любой самостоятельной/контрольной работы.

А чтобы помочь вам в этом нелёгком деле, предлагаю скачать на моём сайте комплект уравнений для самостоятельного решения. Ко всем уравнениям есть ответы, поэтому вы всегда сможете себя проверить.

В общем, желаю удачной тренировки. И увидимся в следующем уроке — там мы будем разбирать действительно сложные показательные уравнения, где описанных выше способов уже недостаточно. И простой тренировки тоже будет недостаточно.:)

Смотрите также:

1. Преобразование показательных уравнений
2. Решение показательных неравенств
3. Тест по теории вероятностей (1 вариант)
4. Общая схема решения задач B15
5. Задачи на проценты: считаем проценты с помощью пропорции
6. Более сложные задачи на производительность

Как определить степень уравнения

Уравнение представляет собой математическое соотношение, которое отражает равенство двух алгебраических выражений. Чтобы определить его степень, необходимо внимательно посмотреть на все присутствующие в нем переменные.

Инструкция

1

Решение любого уравнения сводится к нахождению таких значений переменной х, которые после подстановки в исходное уравнение дают верное тождество – выражение, не вызывающее никаких сомнений.

2

Степень уравнения – это максимальный или наибольший показатель степени переменной, присутствующей в уравнении. Чтобы ее определить, достаточно обратить внимание на значение степеней имеющихся переменных. Максимальная величина и определяет степень уравнения.

3

Уравнения бывают разных степеней. К примеру, линейные уравнения вида ax+b=0 имеют первую степень. В них присутствуют только неизвестные в названной степени и числа. Важно отметить отсутствие дробей с неизвестной величиной в знаменателе. Любое линейное уравнение сводится к изначальному виду: ax+b=0, где b может являться любым числом, а a – любым, но не равным 0. Если вы привели запутанное и длинное выражение к надлежащему виду ax+b=0, можно с легкостью найти не более одного решения.

4

Если в уравнении есть неизвестное во второй степени, оно является квадратным. Кроме того, в нем могут быть и неизвестные в первой степени, и числа, и коэффициенты. Но в таком уравнении отсутствуют дроби с переменной в знаменателе. Любое квадратное уравнение, подобно линейному, сводится к виду: ax^2+bx +c=0. Здесь a, b и с – любые числа, при этом число a не должно быть равным 0. Если, упрощая выражение, вы обнаружили уравнение вида ax^2+bx+c=0, дальнейшее решение довольно простое и предполагает не более двух корней. В 1591 году Франсуа Виет вывел формулы для нахождения корней квадратных уравнений. А Евклид и Диофант Александрийский, Аль-Хорезми и Омар Хайям использовали геометрические способы нахождения их решений.

5

Существует также и третья группа уравнений, которая называется дробными рациональными уравнениями. Если в исследуемом уравнении присутствуют дроби с переменной в знаменателе, то это уравнение – дробное рациональное или же просто дробное. Чтобы найти решения таких уравнений, надо всего лишь уметь с помощью упрощений и преобразований сводить их к рассмотренным двум известным типам.

6

Все остальные уравнения составляют четвертую группу. Их больше всего. Сюда входят и кубические, и логарифмические, и показательные, и тригонометрические их разновидности.

7

Решение кубических уравнений состоит также в упрощении выражений и нахождении не более 3 корней. Уравнения, имеющие более высокую степень, решаются разными способами, в том числе и графическим, когда на основе известных данных рассматриваются построенные графики функций и отыскиваются точки пересечений линий графиков, координаты которых и являются их решениями.

Всем привет! 🖐🖐🖐

🎯 В этой статье мы разберемся как отличить и как решать уравнение 4 степени!
🎯 Задания из ЕГЭ, ОГЭ, ВПР, иногда из учебников

✅ Решения подробные, будет понятно 😎
✅ В конце задания для тренировки 💪
✅ В комментах отвечу на ваши вопросы 😊
✅ И без лишней воды ☔☔☔

Вот какие уравнения мы разберем сегодня:

📝 Как отличить и как решать уравнение 4 степени

Рассматриваем чем отличается уравнение 4 степени.

Способы решения:
◽ группировка и вынесение общего множителя
◽ деление столбиком многочлена на скобку (теорема Безу)
◽ формулы сокращенного умножения
◽ замена

Скрин:

📝 Уравнение 1

Как решить такие простые уравнения 4 степени? Избавляемся от 4 степени.

Скрины решения:

📝 Уравнение 2

Данное уравнение 4 степени является биквадратным. Делаем замену x²=t.

Скрины решения:

📝 Уравнение 3

Решаем:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 4

Способы решения:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 5

Решаем с помощью замены, сводим к квадратному уравнению.

Скрины решения:

📝 Уравнение 6

Решаем с помощью замены, в итоге сводим к квадратному уравнению.

Скрины решения:

А вот такую замену предложил сделать один мой зритель, очень удобно. Для замены на конце выражения выбирается +5, то есть число, которое находится посередине между +4 и +6. Этот способ замены дает возможность свернуть по формуле сокращенного умножения.

📝 Уравнение 7

Решаем это уравнение с учетом его особенности – в левой части стоит сумма квадратов.

Скрины решения:

📝 Уравнение 8

Способы решения:
◽ 1 способ – разложить на множители
◽ 2 способ – формула сокращенного умножения
◽ 3 способ – избавиться от квадратов

Скрины решения:

📝 Уравнение 9

Способы решения:
◽ 1 способ – формула сокращенного умножения
◽ 2 способ – понизить степень уравнения

Скрины решения:

📝 Уравнение 10

Сначала раскрываем скобки и после этого решаем как биквадратное.

Скрины решения:

📝 Задания для тренировки

Реши сам по аналогии и напиши свои ответы в комментариях! 😋😋😋

⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜

✅ Оглавление:

👉 Как решать любое уравнение (цикл занятий) здесь

✍ Занятие 0 Виды уравнений здесь
✍ Занятие 1 Линейное уравнение здесь
✍ Занятие 2 Часть 1 Полные квадратные уравнения здесь
✍ Занятие 2 Часть 2 Неполные квадратные уравнения здесь
✍ Занятие 2 Часть 3 Квадратные уравнения со скобками здесь
✍ Занятие 3 Часть 1 Стандартные кубические уравнения здесь
✍ Занятие 3 Часть 2 Кубические уравнения со скобками здесь
✍ Занятие 4 Уравнение 4 степени здесь
✍ Занятие 5 Уравнение со скобками (вида Произведение = 0) здесь
✍ Занятие 6 Уравнение со скобками (вида Произведение = выр) здесь
✍ Занятие 7 Дробное уравнение (вида Дробь = 0) здесь
✍ Занятие 8 Дробное уравнение (вида Дробь = выражению) здесь
✍ Занятие 9 Иррациональное уравнение (с корнями) здесь
✍ Занятие 10 Уравнение с модулем здесь
✍ Занятие 11 Часть 1 Простые показательные уравнения здесь
✍ Занятие 11 Часть 2 Сложные показательные уравнения здесь
✍ Занятие 12 Часть 1 Простые логарифмические уравнения здесь
✍ Занятие 12 Часть 2 Сложные логарифмические уравнения здесь
✍ Занятие 13 Тригонометрическое уравнение здесь
✍ Занятие 14 Уравнение смешанного типа здесь

🧭 Путеводитель по каналу Подслушано по Математике

здесь