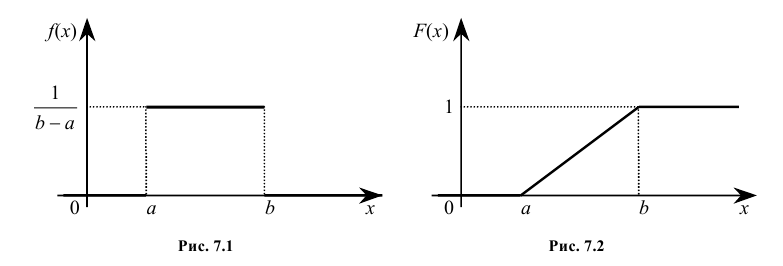
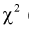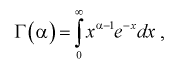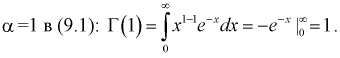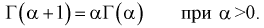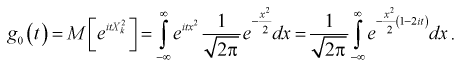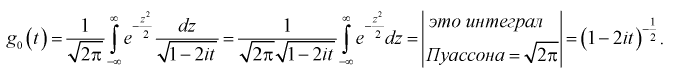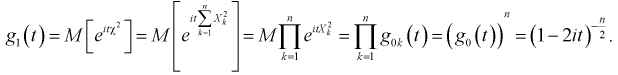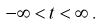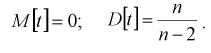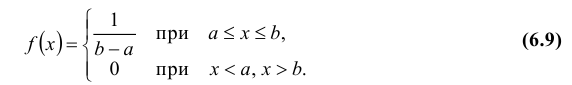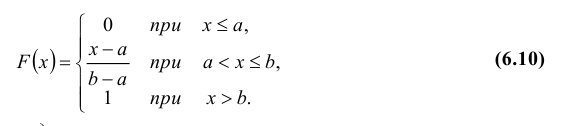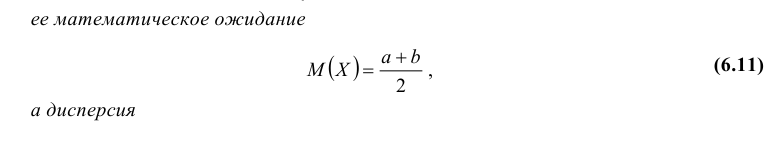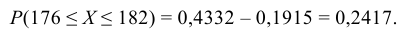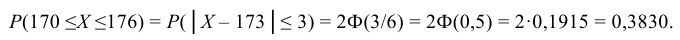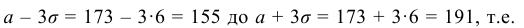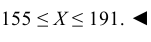На чтение 16 мин Просмотров 125к. Опубликовано 25 мая, 2018
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда
Вероятность подходящих событий + вероятность неподходящих событий = 1
Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Содержание
- Вероятность нескольких событий
- Задачи и решения задач на вероятность
- Вероятность нескольких событий
- Дополняющая вероятность
Вероятность нескольких событий
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем.
Задачи и решения задач на вероятность
Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.
Решение:
Вероятность, это отношение благоприятных вариантов к общему их количеству.
Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.
Вероятность тогда:
Ответ: 0,8.
Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?
Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.
Вероятность что первый дежурный мальчик:
Вероятность что второй дежурный мальчик:
Раз оба должны быть мальчики, вероятности перемножим:
Ответ: 0,2.
Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.
Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.
Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.
Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.
Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.
Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).
Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.
Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.
Задача 10.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.
Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?
Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.
Задача 11.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.
Задача 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.
Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.
Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.
Вероятность нескольких событий
Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Решение:
Тип вопроса: совмещение событий.
Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.
Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
| Игра №1 | Игра №2 | Вероятность данного варианта |
| 3 | 1 | 0,4 · 0,2 = 0,08 |
| 1 | 3 | 0,2 · 0,4 = 0,08 |
| 3 | 3 | 0,4 · 0,4 = 0,16 |
Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.
Решение:
Тип вопроса: уменьшение групп.
Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.
Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение:
Способ №1
Тип задачи: уменьшение групп.
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.
Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют в несколько вариантов:
Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Тип задачи: уменьшение групп.
Способ №1
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:
Орёл ― решка ― орёл;
Орёл ― орёл ― решка;
Решка ― орёл ― орёл;
Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)
Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.
Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Тип вопроса: совмещение событий.
В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.
Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
Тип вопроса: совмещение событий.
Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.
Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.
Решение:
Тип вопроса: совмещение событий.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):
… США, КАН, КИТ …
… США, КИТ, КАН …
… КИТ, США, КАН …
… КАН, США, КИТ …
… КАН, КИТ, США …
… КИТ, КАН, США …
США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:
≈ 0,33.
Дополняющая вероятность
Задача 1.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.
Найдите вероятность того, что случайно выбранная батарейка будет забракована.
Решение:
Существуют 2 варианта, которые нам подходят:
Вариант А: батарейка забракована, она неисправна;
Вариант Б: батарейка забракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;
Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;
Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.
Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение:
Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).
Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.
Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.
Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.
Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.
Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.
Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.
Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.
Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):
| 11 апреля | 12 апреля | 13 апреля | Вероятность данного варианта |
| X – 0,9 | X – 0,9 | O – 0,1 | 0,9 ·0,9 ·0,1 = 0,081 |
| X – 0,9 | O – 0,1 | O – 0,9 | 0,9 ·0,1 ·0,9 = 0,081 |
| O – 0,1 | O – 0,9 | O – 0,9 | 0,1 ·0,9 ·0,9 = 0,081 |
| O – 0,1 | X – 0,1 | O – 0,1 | 0,1 ·0,1 ·0,1 = 0,001 |
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.
Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):
| 4 июля | 5 июля | 6 июля | Вероятность данного варианта |
| X – 0,8 | X – 0,8 | O – 0,2 | 0,8 · 0,8 · 0,2 = 0,128 |
| X – 0,8 | O – 0,2 | O – 0,8 | 0,8 · 0,2 · 0,8 = 0,128 |
| O – 0,2 | O − 0,8 | O − 0,8 | 0,2 · 0,8 · 0,8 = 0,128 |
| O – 0,2 | X – 0,2 | O – 0,2 | 0,2 · 0,2 · 0,2 = 0,008 |
Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.
Загрузить PDF
Загрузить PDF
Вероятность показывает возможность того или иного события при определенном количестве повторений.[1]
Это число возможных результатов с одним или несколькими исходами, поделенное на общее количество возможных событий. Вероятность нескольких событий вычисляется путем разделения задачи на отдельные вероятности с последующим перемножением этих вероятностей.
-
1
Выберите событие со взаимоисключающими результатами. Вероятность можно рассчитать лишь в том случае, если рассматриваемое событие либо происходит, либо не происходит. Нельзя одновременно получить какое-либо событие и противоположный ему результат. Примером таких событий служат выпадение 5 на игровом кубике или победа определенной лошади на скачках. Пять либо выпадет, либо нет; определенная лошадь либо придет первой, либо нет.[2]
Например:” невозможно вычислить вероятность такого события: при одном броске кубика выпадут 5 и 6 одновременно.
-
2
Определите все возможные события и результаты, которые могут произойти. Предположим, необходимо определить вероятность того, что при броске игрового кубика с 6 цифрами выпадет тройка. «Выпадение тройки» является событием, и поскольку мы знаем, что может выпасть любая из 6 цифр, число возможных исходов равно шести. Таким образом, мы знаем, что в данном случае есть 6 возможных результатов и одно событие, вероятность которого мы хотим определить. Ниже приведено еще два примера.[3]
- Пример 1. Какова вероятность того, что вы случайно выберете день, который выпадает на выходные? В данном случае событием является «выбор дня, который приходится на выходные», а число возможных исходов равно количеству дней недели, то есть семи.
- Пример 2. В коробке находятся 4 синих, 5 красных и 11 белых шаров. Если достать из коробки случайный шар, какова вероятность того, что он окажется красным? Событием является «вынуть красный шар», а число возможных исходов равно общему количеству шаров, то есть двадцати.
-
3
Поделите число событий на количество возможных исходов. Таким образом вы определите вероятность одиночного события. Если мы рассматриваем случай выпадения 3 при бросании кубика, число событий равно 1 (тройка находится лишь на одной грани кубика), а общее количество исходов равно 6. В результате получаем соотношение 1/6, 0,166, или 16,6 %. Вероятность события для двух приведенных выше примеров находится следующим образом:[4]
- Пример 1. Какова вероятность того, что вы случайно выберете день, который выпадает на выходные? Число событий равно 2, так как в одной неделе два выходных дня, а общее количество исходов составляет 7. Таким образом, вероятность равна 2/7. Полученный результат можно записать также как 0,285 или 28,5 %.
- Пример 2. В коробке находятся 4 синих, 5 красных и 11 белых шаров. Если достать из коробки случайный шар, какова вероятность того, что он окажется красным? Число событий равно 5, поскольку в коробке 5 красных шаров, а общее количество исходов составляет 20. Находим вероятность: 5/20 = 1/4. Полученный результат можно записать также как 0,25 или 25 %.
-
4
Сложите вероятности всех возможных событий и проверьте, получится ли в сумме 1. Суммарная вероятность всех возможных событий должна составлять 1, или 100 %. Если у вас не получится 100 %, скорее всего, вы допустили ошибку и пропустили одно или несколько возможных событий. Проверьте свои вычисления и убедитесь, что вы учли все возможные исходы.[5]
- Например, вероятность выпадения 3 при бросании игрового кубика составляет 1/6. При этом вероятность выпадения любой другой цифры из пяти оставшихся также равна 1/6. В результате получаем 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6, то есть 100 %.
- Если вы, например, забудете о цифре 4 на кубике, сложение вероятностей даст вам лишь 5/6, или 83 %, что не равно единице и указывает на ошибку.
-
5
Представьте вероятность невозможного исхода в виде 0. Это означает, что данное событие не может произойти, и его вероятность равна 0. Таким образом вы сможете учесть невозможные события.[6]
- Например, если бы вы вычисляли вероятность того, что в 2020 году Пасха придется на понедельник, то получили бы 0, поскольку Пасха всегда празднуется в воскресенье.
Реклама
-
1
При рассмотрении независимых событий вычисляйте каждую вероятность отдельно. После того как вы определите, каковы вероятности событий, их можно будет рассчитать отдельно. Предположим, необходимо узнать вероятность того, что при бросании кубика два раза подряд выпадет 5. Мы знаем, что вероятность выпадения одной пятерки составляет 1/6, и вероятность выпадения второй пятерки также равна 1/6. Первый исход не связан со вторым.[7]
- Несколько выпадений пятерок называются независимыми событиями, поскольку то, что выпадет первый раз, не влияет на второе событие.
-
2
Учитывайте влияние предыдущих исходов при расчете вероятности для зависимых событий. Если первое событие влияет на вероятность второго исхода, говорят о расчете вероятности зависимых событий. Например, если вы выбираете две карты из колоды, состоящей из 52 карт, после взятия первой карты состав колоды изменяется, что влияет на выбор второй карты. Чтобы рассчитать вероятность второго из двух зависимых событий, необходимо вычесть 1 из количества возможных результатов при расчете вероятности второго события.[8]
-
Пример 1. Рассмотрим следующее событие: Из колоды случайным образом одну за другой вытягивают две карты. Какова вероятность того, что обе карты будут иметь трефовую масть? Вероятность того, что первая карта будет иметь трефовую масть, составляет 13/52, или 1/4, поскольку всего в колоде 13 карт одной масти.
- После этого вероятность того, что вторая карта окажется трефовой масти, составляет 12/51, поскольку одной трефовой карты уже нет. Это объясняется тем, что первое событие влияет на второе. Если вы вытянули тройку треф и не положили ее обратно, в колоде будет на одну карту меньше (51 вместо 52).
-
Пример 2. В коробке 4 синих, 5 красных и 11 белых шаров. Если наугад вынуть три шара, какова вероятность того, что первый окажется красным, второй синим, а третий белым?
- Вероятность того, что первый шар окажется красным, составляет 5/20, или 1/4. Вероятность того, что второй шар будет синим, равна 4/19, поскольку в коробке осталось на один шар меньше, но по прежнему 4 синих шара. Наконец, вероятность того, что третий шар окажется белым, составляет 11/18, так как мы уже вынули два шара.
-
Пример 1. Рассмотрим следующее событие: Из колоды случайным образом одну за другой вытягивают две карты. Какова вероятность того, что обе карты будут иметь трефовую масть? Вероятность того, что первая карта будет иметь трефовую масть, составляет 13/52, или 1/4, поскольку всего в колоде 13 карт одной масти.
-
3
Перемножьте вероятности каждого отдельного события. Независимо от того, имеете ли вы дело с независимыми или зависимыми событиями, а также количества исходов (их может быть 2, 3 и даже 10), можно рассчитать общую вероятность, умножив вероятности всех рассматриваемых событий друг на друга. В результате вы получите вероятность нескольких событий, следующих одно за другим. Например, стоит задача Найти вероятность того, что при бросании кубика два раза подряд выпадет 5. Это два независимых события, вероятность каждого из которых равна 1/6. Таким образом, вероятность обоих событий составляет 1/6 x 1/6 = 1/36, то есть 0,027, или 2,7 %.[9]
- Пример 1. Из колоды наугад одну за другой вытягивают две карты. Какова вероятность того, что обе карты будут иметь трефовую масть? Вероятность первого события составляет 13/52. Вероятность второго события равна 12/51. Находим общую вероятность: 13/52 x 12/51 = 12/204 = 1/17, то есть 0,058, или 5,8 %.
- Пример 2. В коробке находятся 4 синих, 5 красных и 11 белых шаров. Если наугад вытянуть из коробки три шара один за другим, какова вероятность того, что первый окажется красным, второй синим, а третий белым? Вероятность первого события составляет 5/20. Вероятность второго события равна 4/19. Вероятность третьего события составляет 11/18. Таким образом, общая вероятность равна 5/20 x 4/19 x 11/18 = 44/1368 = 0,032, или 3,2 %.
Реклама
-
1
Рассматривайте возможность как дробь с положительным результатом в числителе. Вернемся к нашему примеру с разноцветными шарами. Предположим, необходимо узнать вероятность того, что вы достанете белый шар (всего их 11) из всего набора шаров (20). Шанс того, что данное событие произойдет, равен отношению вероятности того, что оно случится, к вероятности того, что оно не произойдет. Поскольку в коробке имеется 11 белых шаров и 9 шаров другого цвета, возможность вытянуть белый шар равна отношению 11:9.[10]
- Число 11 представляет вероятность достать белый шар, а число 9 — вероятность вытянуть шар другого цвета.
- Таким образом, более вероятно, что вы достанете белый шар.
-
2
Сложите полученные величины, чтобы перевести возможность в вероятность. Преобразовать возможность довольно просто. Сначала ее следует разбить на два отдельных события: шанс вытянуть белый шар (11) и шанс вытянуть шар другого цвета (9). Сложите полученные числа, чтобы найти общее число возможных событий. Запишите все как вероятность с общим количеством возможных результатов в знаменателе.[11]
- Вы можете вынуть белый шар 11 способами, а шар другого цвета — 9 способами. Таким образом, общее число событий составляет 11 + 9, то есть 20.
-
3
Найдите возможность так, как если бы вы рассчитывали вероятность одного события. Как мы уже определили, всего существует 20 возможностей, причем в 11 случаях можно достать белый шар. Таким образом, рассчитать вероятность вытянуть белый шар можно так же, как и вероятность любого другого одиночного события. Поделите 11 (количество положительных исходов) на 20 (число всех возможных событий), и вы определите вероятность.[12]
- В нашем примере вероятность достать белый шар составляет 11/20. В результате получаем 11/20 = 0,55, или 55 %.
Реклама
Советы
- Для описания вероятности того, что то или иное событие произойдет, математики обычно используют термин «относительная вероятность». Определение «относительная» означает, что результат не гарантирован на 100 %. Например, если подбросить монету 100 раз, то, вероятно, не выпадет ровно 50 раз орел и 50 решка. Относительная вероятность учитывает это.[13]
- Вероятность какого-либо события не может быть отрицательной величиной. Если у вас получилось отрицательное значение, проверьте свои вычисления.[14]
- Чаще всего вероятности записывают в виде дробей, десятичных дробей, процентов или по шкале от 1 до 10.
- Вам может пригодиться знание того, что в спортивных и букмекерских ставках шансы выражаются как «шансы против» — это означает, что возможность заявленного события оценивается первой, а шансы того события, которое не ожидается, стоят на втором месте. Хотя это и может сбить с толку, важно помнить об этом, если вы собираетесь делать ставки на какое-либо спортивное событие.
Реклама
Об этой статье
Эту страницу просматривали 704 977 раз.
Была ли эта статья полезной?
Привет, сегодня поговорим про вероятность, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
вероятность , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность(и невероятность) бывает большей или меньшей . Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности .
Простой пример: вероятность того, что на кубике выпадет число «5», равна 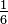
Исследование вероятности с математической точки зрения составляет особую дисциплину — теорию вероятностей . В теории вероятностей и математической статистике понятие вероятности формализуется как числовая характеристика события — вероятностная мера (или ее значение) — мера на множестве событий (подмножеств множества элементарных событий), принимающая значения от 

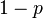
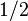
Классическое определение вероятности основано на понятии равновозможности исходов. В качестве вероятности выступает отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. Например, вероятность выпадения «орла» или «решки» при случайном подбрасывании монетки равна 1/2, если предполагается, что только эти две возможности имеют место и они являются равновозможными. Данное классическое «определение» вероятности можно обобщить на случай бесконечного количества возможных значений — например, если некоторое событие может произойти с равной вероятностью в любой точке (количество точек бесконечно) некоторой ограниченной области пространства (плоскости), то вероятность того, что оно произойдет в некоторой части этой допустимой области равна отношению объема (площади) этой части к объему (площади) области всех возможных точек.
Эмпирическое «определение» вероятности связано с частотой наступления события исходя из того, что при достаточно большом числе испытаний частота должна стремиться к объективной степени возможности этого события. В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
Вероятностное описание тех или иных явлений получило широкое распространение в современной науке, в частности в эконометрике, статистической физикемакроскопических (термодинамических) систем, где даже в случае классического детерминированного описания движения частиц детерминированное описание всей системы частиц не представляется практически возможным и целесообразным. В квантовой физике сами описываемые процессы имеют вероятностную природу.
История теории вероятностей
Христиан Гюйгенс, вероятно, опубликовал первую книгу по теории вероятностей
Предыстория понятия вероятности
Необходимость понятия вероятности и исследований в этом направлении была исторически связана с азартными играми, особенно с играми в кости. До появления понятия вероятности формулировались в основном комбинаторные задачи подсчета числа возможных исходов при бросании нескольких костей, а также задача раздела ставки между игроками, когда игра закончена досрочно. Первую задачу при бросании трех костей «решил» в 960 году епископ Виболд из г. Камбрэ . Он насчитал 56 вариантов. Однако это количество по сути не отражает количество равновероятных возможностей, поскольку каждый из 56 вариантов может реализоваться разным количеством способов. В первой половине 13 века эти аспекты учел Ришар де Форниваль. Несмотря на то, что у него тоже фигурирует число 56, но он в рассуждениях учитывает, что, например, «одинаковое количество очков на трех костях можно получить шестью способами». Основываясь на его рассуждениях уже можно установить, что число равновозможных вариантов — 216. В дальнейшем многие не совсем верно решали эту задачу. Впервые четко количество равновозможных исходов при подбрасывании трех костей подсчитал Галилео Галилей, возводя шестерку (количество вариантов выпадения одной кости) в степень 3 (количество костей): 6³=216. Он же составил таблицы количества способов получения различных сумм очков.
Задачи второго типа в конце 15 века сформулировал и предложил первое (вообще говоря ошибочное) решение Лука Пачоли . Его решение заключалось в делении ставки пропорционально уже выигранным партиям. Существенное дальнейшее продвижение в начале 16 века связано с именами итальянских ученых Джероламо Кардано и Н. Тарталья. Кардано дал правильный подсчет количества случаев при бросании двух костей (36). Он также впервые соотнес количество случаев выпадения некоторого числа хотя бы на одной кости (11) к общему числу исходов (что соответствует классическому определению вероятности) — 11/36. Аналогично и для трех костей он рассматривал, например, что девять очков может получиться количеством способов, равным 1/9 «всей серии» (то есть общего количества равновозможных исходов — 216). Кардано формально не вводил понятие вероятности, но по существу рассматривал относительное количество исходов, что по сути эквивалентно рассмотрению вероятностей. Необходимо также отметить, что в зачаточном состоянии у Кардано можно найти также идеи, связанные с законом больших чисел. По поводу задачи деления ставки Кардано предлагал учитывать количество оставшихся партий, которые надо выиграть. Н. Тарталья также сделал замечания по поводу решения Луки и предложил свое решение (вообще говоря, тоже ошибочное).
Заслуга Галилея также заключается в расширении области исследований на область ошибок наблюдений. Он впервые указал на неизбежность ошибок и классифицировал их на систематические и случайные (такая классификация применяется и сейчас).
Возникновение понятия и теории вероятностей
Первые работы об учении о вероятности относится к 17 веку. Такие как переписка французских ученых Б. Паскаля, П. Ферма (1654 год) и голландского ученого X. Гюйгенса (1657 год) давшего самую раннюю из известных научных трактовок вероятности . По существу Гюйгенс уже оперировал понятием математического ожидания. Швейцарский математик Я. Бернулли, установил закон больших чисел для схемы независимых испытаний с двумя исходами (посмертно, 1713 год).
В XVIII в. — начале ХIХ в. теория вероятностей получает развитие в работах А. Муавра (Англия)(1718 год), П. Лаплас (Франция), К. Гаусса(Германия) и С. Пуассона (Франция). Теория вероятностей начинает применяться в теории ошибок наблюдений, развившейся в связи с потребностями геодезии и астрономии, и в теории стрельбы. Необходимо отметить, что закон распределения ошибок по сути предложил Лаплас сначала как экспоненциальная зависимость от ошибки без учета знака (в 1774 год), затем как экспоненциальную функцию квадрата ошибки (в 1778 году). Последний закон обычно называют распределением Гаусса или нормальным распределением. Бернулли (1778 год) ввел принцип произведения вероятностей одновременных событий. Адриен Мари Лежандр (1805) разработал метод наименьших квадратов.
Во второй половине XIX в. развитие теории вероятностей связано с работами русских математиков П. Л. Чебышева, А. М. Ляпунова и А. А. Маркова (старшего), а также работы по математической статистике А. Кетле (Бельгия) и Ф. Гальтона (Англия) и статистической физике Л. Больцмана (в Австрия), которые создали основу для существенного расширения проблематики теории вероятностей. Наиболее распространенная в настоящее время логическая (аксиоматическая) схема построения основ теории вероятностей разработана в 1933 советским математиком А. Н. Колмогоровым.
Определения вероятности
Классическое определение
Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).
Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.
Классическое определение вероятности можно сформулировать следующим образом:
Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.
Геометрическое определение
Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум, не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случае, обобщая классическое определение, можно прийти к геометрическому определению вероятности попадания в подобласть 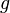
В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от ее площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объема». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объема обобщается до понятия меры некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объем» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность.
Частотное (статистическое) определение
Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно, существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:
где 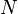
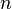
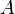
Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности — путем большого количества однородных и независимых наблюдений — тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к 
Аксиоматическое определение
В современном математическом подходе вероятность задается аксиоматикой Колмогорова. Предполагается, что задано некоторое пространство элементарных событий 
Вероятностью (вероятностной мерой) называется мера (числовая функция) 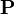
- Неотрицательность:
,
- Конечность (ограниченность единицей):
,
В случае если пространство элементарных событий X конечно, то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счетного или несчетного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счетная или сигма-аддитивность, то есть выполнение свойства аддитивности для любого не более чем счетного семейства попарно несовместных событий. Это необходимо для обеспечения «непрерывности» вероятностной меры.
Вероятностная мера может быть определена не для всех подмножеств множества 
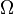
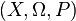
Свойства вероятности
Основные свойства вероятности проще всего определить, исходя из аксиоматического определения вероятности.
1) вероятность невозможного события (пустого множества 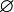
Это следует из того, что каждое событие можно представить как сумму этого события и невозможного события, что в силу аддитивности и конечности вероятностной меры означает, что вероятность невозможного события должна быть равна нулю.
2) если событие A «входит» в событие B, то есть 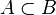
Это следует из неотрицательности и аддитивности вероятностной меры, так как событие 
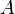
3) вероятность каждого события 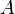
Первая часть неравенства (неотрицательность) утверждается аксиоматически, а вторая следует из предыдущего свойства с учетом того, что любое событие «входит» в 


4) вероятность наступления события 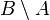
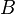
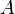
Это следует из аддитивности вероятности для несовместных событий и из того, что события 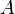
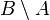
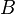
5) вероятность события 
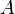
Это следует из предыдущего свойства, если в качестве множества 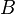


6) (теорема сложения вероятностей) вероятность наступления хотя бы одного из (то есть суммы) произвольных (не обязательно несовместных) двух событий 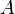
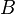
Это свойство можно получить, если представить объединение двух произвольных множеств как объединение двух непересекающихся — первого и разности между вторым и пересечением исходных множеств: 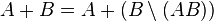
Условная вероятность
Вероятность наступления события 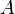
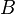
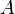
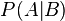
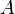
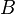
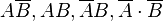
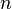
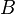
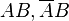
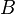

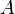
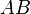
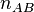
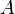
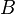
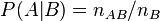
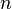
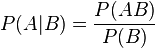
Отсюда следует так называемая теорема умножения вероятностей:
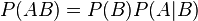
В силу симметрии, аналогично можно показать, что также 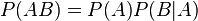
Независимость событий
События A и B называются независимыми, если вероятность наступления одного из них не зависит от того, наступили или нет другие события. С учетом понятия условной вероятности это означает, что 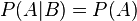
В рамках аксиоматического подхода данная формула принимается как определение понятия независимости двух событий. Для произвольной (конечной) совокупности событий 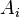
Выведенная (в рамках классического определения вероятности) выше формула условной вероятности при аксиоматическом определении вероятности является определением условной вероятности. Соответственно, как следствие определений независимых событий и условной вероятности получается равенство условной и безусловной вероятностей события.
Полная вероятность и формула Байеса
Набор событий 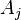
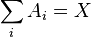
Пусть имеется полный набор попарно несовместных событий 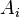
Тогда вышеописанную формулу Байеса с учетом полной вероятности можно записать в следующем виде:
Данная формула является основой альтернативного подхода к вероятности — байесовского или субъективного подхода (см. ниже).
Вероятность и случайные величины
Важнейший частный случай применения «вероятности» — вероятность получения в результате испытания или наблюдения того или иного числового значения некоторой измеряемой (наблюдаемой) величины. Предполагается, что до проведения испытания (наблюдения) точное значение этой величины неизвестно, то есть имеется явная неопределенность, связанная обычно (за исключением квантовой физики) с невозможностью учета всех факторов, влияющих на результат. Такие величины называют случайными. В современной теории вероятностей понятие случайной величины формализуется и она определяется как функция «случая» — функция на пространстве элементарных событий. При таком определении наблюдаются не сами элементарные события, а «реализации», конкретные значения случайной величины. Например, при подбрасывании монетки выпадает «решка» или «орел». Если ввести функцию, ставящую в соответствие «решке» — число 1, а «орлу» — 0, то получим случайную величину как функцию указанных исходов. При этом понятие случайной величины обобщается на функции, отображающие пространство элементарных событий в некоторое пространство произвольной природы, соответственно можно ввести понятия случайного вектора, случайного множества и т. д. Однако, обычно под случайной величиной подразумевают именно числовую функцию (величину).
Отвлекаясь от описанной формализации под пространством элементарных событий можно понимать множество возможных значений случайной величины. Сигма-алгеброй подмножеств являются произвольные интервалы на числовой оси, их всевозможные (счетные) объединения и пересечения. Вероятностную меру называют в данном случае распределением случайной величины. Достаточно задать вероятностную меру для интервалов вида 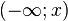
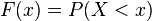
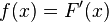

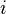

Доска Гальтона — демонстрируетнормальное распределение
Распределение случайной величины дает ее полную характеристику. Однако, часто используют отдельные характеристики этого распределения. В первую очередь это математическое ожидание случайной величины — среднее ожидаемое значение случайной величины с учетом взвешивания по вероятностям появления тех или иных значений, и дисперсия или вариация — средний квадрат отклонения случайной величины от ее математического ожидания. В некоторых случаях используются и иные характеристики, среди которых важное значение имеют асимметрия и эксцесс. Описанные показатели являются частными случаями так называемых моментов распределения.
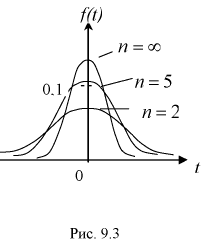
Существуют некоторые стандартные законы распределения, часто используемые на практике. В первую очередь — этонормальное распределение (распределение Гаусса). Оно полностью характеризуется двумя параметрами — математическим ожиданием и дисперсией. Его широкое использование связано, в частности, с так называемымипредельными теоремами (см. ниже). При проверке гипотез часто возникают распределения Хи-квадрат, распределение Стьюдента, распределение Фишера. При анализе дискретных случайных величин рассматриваются биномиальное распределение, распределение Пуассона и др. Также часто рассматривается гамма-распределение, частным случаем которого является экспоненциальное распределение, а также указанное выше распределение Хи-квадрат Естественно, используемые на практике распределения не ограничиваются только этими распределениями.
Часто на практике исходя из априорных соображений делается предположение, что распределение вероятностей данной случайной величины относится к некоторому известному с точностью до параметров распределению. Например, к тому же нормальному распределению, но с неизвестным математическим ожиданием и дисперсией (эти два параметра однозначно определяют все нормальное распределение). Задачей статистических наук (математическая статистика, эконометрика и т. д.) в таком случае является оценка значений этих параметров наиболее эффективным (точным) способом. Существуют критерии, с помощью которых можно установить степень «истинности» соответствующих методов оценки. Обычно требуется как минимум состоятельность оценки, несмещенность и эффективность в некотором классе оценок.
На практике применяются также непараметрические методы оценки распределений.
Законы больших чисел
Важнейшее значение в теории вероятностей и в ее приложениях имеет группа теорем, объединяемых обычно под названием «закон больших чисел» илипредельных теорем. Не прибегая к строгим формулировкам, можно сказать, например, что при некоторых слабых условиях среднее значение независимых одинаково распределенных случайных величин стремится к их математическому ожиданию при достаточно большом количестве этих случайных величин. Если в качестве совокупности случайных величин рассматривать независимые наблюдения одной и той же случайной величины, то это означает, что среднее по выборочным наблюдениям должно стремиться к истинному (неизвестному) математическому ожиданию этой случайной величины. Это закон больших чисел в форме Чебышева. Это дает основу для получения соответствующих оценок.
Весьма частным, но очень важным случаем является схема Бернулли — независимые испытания, в результате которых некоторое событие либо происходит, либо нет. Предполагается, что в каждом испытании вероятность наступления события одинакова и равна 

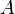




Наряду с указанными теоремами существует так называемая центральная предельная теорема, которая дает предельное распределение вероятностей для средней, а именно, при определенных слабых условиях среднее значение наблюдений случайной величины при достаточно большом количестве наблюдений имеют нормальное распределение (независимо от исходного распределения самой случайной величины). Например, такое имеет место для среднего значения независимых одинаково распределенных случайных величин. В частности эта теорема применима и к схеме Бернулли. Вообще количество появлений события A в n испытаниях имеетбиномиальное распределение, однако при достаточно большом количестве наблюдений это распределение согласно указанной теореме стремится к нормальному распределению в данном случае с математическим ожиданием 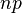
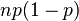


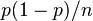
Байесовский подход к вероятности
В основе вышеописанного объективного (частотного) подхода лежит предположение о наличии объективной неопределенности, присущей изучаемым явлениям. В альтернативном байесовском подходе неопределенность трактуется субъективно — как мера нашего незнания. В рамках байесовского подхода под вероятностью понимается степень уверенности в истинности суждения — субъективная вероятность.
Идея байесовского подхода заключается в переходе от априорных знаний к апостерирорным с учетом наблюдаемых явлений. Суть байесовского подхода следует из описанной выше формулы Байеса. Пусть имеются полный набор гипотез 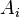
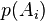
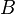
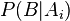
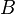
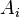
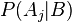
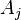
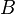
В частности в отличие от базового подхода к оценке распределений случайных величин, где предполагается, что на основе наблюдений оцениваются значения неизвестных параметров распределений, в байесовском подходе предполагается что параметры — тоже случайные величины (с точки зрения нашего незнания их значений). В качестве гипотез выступают те или иные возможные значения параметров и предполагаются данными некоторые априорные плотности неизвестных параметров 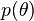
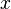

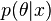
Вероятность, информация и энтропия
Пусть имеется 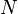
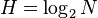
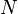
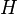
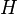
В общем случае (исходы не обязательно равновероятны) количество информации, связанное с реализацией одного из 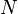

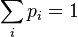
где 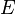
Очевидно, при равновероятности всех исходов (
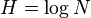
Указанную величину называют информацией, информационным количеством, информационной энтропией и т. д. Необходимо отметить, что такое определение информации абстрагируется от какого-либо содержания информации, содержания конкретных исходов. Информационное количество определяется только на основе вероятностей. Величину 
Вероятность и квантовая физика
В квантовой механике состояние системы (частицы) характеризуется волновой функцией (вообще говоря вектором состояния) — комплекснозначной функцией «координат», квадрат модуля которого интерпретируется как плотность вероятности получения заданных значений «координат». Согласно современным представлениям вероятностное определение состояния является полным и причиной вероятностного характера квантовой физики не являются какие-либо «скрытые» факторы — это связано с природой самих процессов. В квантовой физике оказываются возможными любые взаимопревращения различных частиц, не запрещенные теми или иными законами сохранения. И эти взаимопревращения подчиняются закономерностям — вероятностным закономерностям. По современным представлениям принципиально невозможно предсказать ни момент взаимопревращения, ни конкретный результат. Можно лишь говорить о вероятностях тех или иных процессов превращения. Вместо точных классических величин в квантовой физике возможна только оценка средних значений (математических ожиданий) этих величин, например, среднее время жизни частицы.
Вероятность в других сферах
Кроме вопроса о вероятности факта, может возникать, как в области права, так и в области нравственной (при известной этической точке зрения) вопрос о том, насколько вероятно, что данный частный факт составляет нарушение общего закона. Этот вопрос, служащий основным мотивом в религиозной юриспруденцииТалмуда, вызвал и в римско-католическом нравственном богословии (особенно с конца XVI века) весьма сложные систематические построения и огромную литературу,догматическую и полемическую (см. Пробабилизм) .
См. также
- Пробабилизм
- Мера множества
- Риск
- Формула полной вероятности
- Формула Бернулли
- Условная вероятность
- Случайная величина
- Случайность
- Измерение (квантовая механика)
- Квантовая вероятность
- Принцип неопределенности
- Вероятность перехода
- Парадокс закономерности
- Метод Монте-Карло
- геометрическая вероятность , игла буффона , игла буйвола , интегральная геометрия ,
Я хотел бы услышать твое мнение про вероятность Надеюсь, что теперь ты понял что такое вероятность
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория вероятностей. Математическая статистика и Стохастический анализ
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
Простой пример: вероятность того, что на кубике выпадет число «5» (как и для любого другого числа), равна
Вероя́тность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей[1]. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднена. Возможны различные градации «уровней» вероятности[2].
Исследование вероятности с математической точки зрения составляет особую дисциплину — теорию вероятностей[1]. В теории вероятностей и математической статистике понятие вероятности формализуется как числовая характеристика события — вероятностная мера (или её значение) — мера на множестве событий (подмножеств множества элементарных событий), принимающая значения от 





Классическое определение вероятности основано на понятии равновозможности исходов. В качестве вероятности выступает отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. Например, вероятности выпадения «орла» или «решки» при случайном подбрасывании монеты одинаковы и равны 

Эмпирическое «определение» вероятности связано с частотой наступления события исходя из того, что при достаточно большом числе испытаний частота должна стремиться к объективной степени возможности этого события. В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
Вероятностное описание тех или иных явлений получило широкое распространение в современной науке, в частности в эконометрике, статистической физике макроскопических (термодинамических) систем, где даже в случае классического детерминированного описания движения частиц детерминированное описание всей системы частиц не представляется практически возможным и целесообразным. В квантовой физике сами описываемые процессы имеют вероятностную природу.
История[править | править код]
Предыстория понятия вероятности[править | править код]
Необходимость понятия вероятности и исследований в этом направлении была исторически связана с азартными играми, особенно с играми в кости. До появления понятия вероятности формулировались в основном комбинаторные задачи подсчёта числа возможных исходов при бросании нескольких костей, а также задача раздела ставки между игроками, когда игра закончена досрочно. Первую задачу при бросании трёх костей «решил» в 960 году епископ Виболд из г. Камбре[3]. Он насчитал 56 вариантов. Однако это количество по сути не отражает количество равновероятных возможностей, поскольку каждый из 56 вариантов может реализоваться разным количеством способов. В первой половине XIII века эти аспекты учёл Ришар де Форниваль. Несмотря на то, что у него тоже фигурирует число 56, но он в рассуждениях учитывает, что, например, «одинаковое количество очков на трёх костях можно получить шестью способами». Основываясь на его рассуждениях уже можно установить, что число равновозможных вариантов — 216. В дальнейшем многие не совсем верно решали эту задачу. Впервые чётко количество равновозможных исходов при подбрасывании трёх костей подсчитал Галилео Галилей, возводя шестёрку (количество вариантов выпадения одной кости) в степень 3 (количество костей): 6³=216. Он же составил таблицы количества способов получения различных сумм очков.
Задачи второго типа в конце XV века сформулировал и предложил первое (вообще говоря ошибочное) решение Лука Пачоли[3]. Его решение заключалось в делении ставки пропорционально уже выигранным партиям. Существенное дальнейшее продвижение в начале XVI века связано с именами итальянских учёных Джероламо Кардано и Н. Тарталья. Кардано дал правильный подсчёт количества случаев при бросании двух костей (36). Он также впервые соотнес количество случаев выпадения некоторого числа хотя бы на одной кости (11) к общему числу исходов (что соответствует классическому определению вероятности) — 11/36. Аналогично и для трёх костей он рассматривал, например, что девять очков может получиться количеством способов, равным 1/9 «всей серии» (то есть общего количества равновозможных исходов — 216). Кардано формально не вводил понятие вероятности, но по существу рассматривал относительное количество исходов, что по сути эквивалентно рассмотрению вероятностей. В зачаточном состоянии у Кардано можно найти также идеи, связанные с законом больших чисел. По поводу задачи деления ставки Кардано предлагал учитывать количество оставшихся партий, которые надо выиграть. Н. Тарталья также сделал замечания по поводу решения Луки и предложил своё решение (вообще говоря, тоже ошибочное).
Заслуга Галилея также заключается в расширении области исследований на область ошибок наблюдений. Он впервые указал на неизбежность ошибок и классифицировал их на систематические и случайные (такая классификация применяется и сейчас).
Возникновение понятия и теории вероятностей[править | править код]
Первые работы о вероятности относятся к XVII веку. Такие как переписка французских учёных Б. Паскаля, П. Ферма (1654 год) и нидерландского учёного X. Гюйгенса (1657 год) давшего самую раннюю из известных научных трактовок вероятности[4]. По существу Гюйгенс уже оперировал понятием математического ожидания. Швейцарский математик Я. Бернулли установил закон больших чисел для схемы независимых испытаний с двумя исходами (результат был опубликован в 1713 году, уже после его смерти).
В XVIII в. — начале XIX в. теория вероятностей получает развитие в работах А. Муавра (Англия, 1718 год), П. Лаплас (Франция), К. Гаусса (Германия) и С. Пуассона (Франция). Теория вероятностей начинает применяться в теории ошибок наблюдений, развившейся в связи с потребностями геодезии и астрономии, и в теории стрельбы. Закон распределения ошибок по сути предложил Лаплас сначала как экспоненциальную зависимость от ошибки без учёта знака (в 1774 году), затем как экспоненциальную функцию квадрата ошибки (в 1778 году). Последний закон обычно называют распределением Гаусса или нормальным распределением.
Бернулли (1778 год) ввёл принцип произведения вероятностей одновременных событий. Адриен Мари Лежандр (1805) разработал метод наименьших квадратов.
Андрей Николаевич Колмогоров
Во второй половине XIX в. развитие теории вероятностей связано с работами русских математиков П. Л. Чебышёва, А. М. Ляпунова и А. А. Маркова (старшего), а также работы по математической статистике А. Кетле (Бельгия) и Ф. Гальтона (Англия) и статистической физике Л. Больцмана (в Австрии), которые создали основу для существенного расширения проблематики теории вероятностей. Наиболее распространённая в настоящее время логическая (аксиоматическая) схема построения основ теории вероятностей разработана в 1933 советским математиком А. Н. Колмогоровым.
Определения вероятности[править | править код]
Классическое определение[править | править код]
Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).
Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идёт об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру, при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.
Классическое определение вероятности можно сформулировать следующим образом:
Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно 36 (так как на каждый из 6 возможных исходов одной кости возможно по 6 вариантов исхода другой). Оценим вероятность выпадения семи очков. Получить 7 очков можно лишь при следующих сочетаниях исходов броска двух костей: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих получению 7 очков, из 36 возможных исходов броска костей. Следовательно, вероятность будет равна 6/36 или, если сократить, 1/6. Для сравнения: вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.
Геометрическое определение[править | править код]
Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум, не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случае, обобщая классическое определение, можно прийти к геометрическому определению вероятности попадания в подобласть 
В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от её площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объёма». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объёма обобщается до понятия меры некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объём» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность.
Частотное (статистическое) определение[править | править код]
Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно, существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому ещё на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:

где 


Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности — путём большого количества однородных и независимых наблюдений — тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к 
Философские проблемы обоснования[править | править код]
К моменту создания теории вероятностей основой математики были два класса объектов — числа и геометрические фигуры. Для теории вероятностей потребовалось добавить в этот список совершенно особый объект: случайное событие, а также тесно связанные с ним понятия (вероятность, случайная величина и др.). Своеобразие новой науки проявлялось и в том, что её утверждения носили не безусловный характер, как ранее было принято в математике, а предположительно-вероятностный. Поэтому долгое время не прекращались споры о том, можно ли считать идеализированное событие математическим понятием (и тогда теория вероятностей есть часть математики) или же это факт, наблюдаемый в опыте (и тогда теорию вероятностей следует отнести к естественным наукам).
По мнению Давида Гильберта, теория вероятностей родственна механике, то есть представляет собой математизированную «физическую дисциплину»[5]. Август де Морган и его последователь У. С. Джевонс считали базовым понятием «субъективную вероятность», то есть количественную меру нашего понимания предмета исследования, и связывали теорию вероятностей с логикой[6]. Проблемы, связанные с неоднозначной субъективной вероятностью, неоднократно обсуждались, их часто формулируют в виде «вероятностных парадоксов» (см., например, «парадокс трёх узников» или «парадокс мальчика и девочки»). Формализацию субъективной вероятности, совместимую с колмогоровской, предложили Бруно де Финетти (1937) и Леонард Сэвидж (1954).
Во второй половине XX века Альфред Реньи и А. Н. Колмогоров исследовали возможность дать обоснование теории вероятностей на базе теории информации[7]. В наши дни «сложилось чёткое понимание того, что теория вероятностей является подлинно математической наукой, имеющей вместе с тем самые тесные и непосредственные связи с широким спектром наук о природе, а также с техническими и социально-экономическими дисциплинами»[8].
Несмотря на доказанную практикой эффективность вероятностных методов, роль случайности в природе, причина и границы статистической устойчивости остаются предметом дискуссий[9]. «За 200 лет, прошедших со времен Лапласа и Гаусса, наука не добилась продвижения в фундаментальном вопросе — когда возникает статистическая устойчивость»[10].
Аксиоматическое определение[править | править код]
В современном математическом подходе вероятность задаётся аксиоматикой Колмогорова. Предполагается, что задано некоторое пространство элементарных событий 
Вероятностью (вероятностной мерой) называется мера (числовая функция) 
В случае если пространство элементарных событий X конечно, то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счётного или несчётного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счётная или сигма-аддитивность, то есть выполнение свойства аддитивности для любого не более чем счётного семейства попарно несовместных событий. Это необходимо для обеспечения «непрерывности» вероятностной меры.
Вероятностная мера может быть определена не для всех подмножеств множества 


Свойства вероятности[править | править код]
Основные свойства вероятности проще всего определить, исходя из аксиоматического определения вероятности.
1) вероятность невозможного события (пустого множества 
Это следует из того, что каждое событие можно представить как сумму этого события и невозможного события, что в силу аддитивности и конечности вероятностной меры означает, что вероятность невозможного события должна быть равна нулю.
2) если событие A включается («входит») в событие B, то есть 
Это следует из неотрицательности и аддитивности вероятностной меры, так как событие 


3) вероятность каждого события 
Первая часть неравенства (неотрицательность) утверждается аксиоматически, а вторая следует из предыдущего свойства с учётом того, что любое событие «входит» в 


4) вероятность наступления события 



Это следует из аддитивности вероятности для несовместных событий и из того, что события 


5) вероятность события 

Это следует из предыдущего свойства, если в качестве множества 


6) (теорема сложения вероятностей) вероятность наступления хотя бы одного из (то есть суммы) произвольных (не обязательно несовместных) двух событий 

Это свойство можно получить, если представить объединение двух произвольных множеств как объединение двух непересекающихся — первого и разности между вторым и пересечением исходных множеств: 
Условная вероятность[править | править код]
Формула Байеса[править | править код]
Вероятность наступления события 


















.
Отсюда следует так называемая теорема умножения вероятностей:
.
В силу симметрии, аналогично можно показать, что также 
Независимость событий[править | править код]
События A и B называются независимыми, если вероятность наступления одного из них не зависит от того, наступило ли другое событие. С учётом понятия условной вероятности это означает, что 
В рамках аксиоматического подхода данная формула принимается как определение понятия независимости двух событий. Для произвольной (конечной) совокупности событий 
Выведенная (в рамках классического определения вероятности) выше формула условной вероятности при аксиоматическом определении вероятности является определением условной вероятности. Соответственно, как следствие определений независимых событий и условной вероятности, получается равенство условной и безусловной вероятностей события.
Полная вероятность и формула Байеса[править | править код]
Набор событий 

Пусть имеется полный набор попарно несовместных событий 

Тогда вышеописанную формулу Байеса с учётом полной вероятности можно записать в следующем виде:

Данная формула является основой альтернативного подхода к вероятности — байесовского или субъективного подхода (см. ниже).
Вероятность и случайные величины[править | править код]
Важнейший частный случай применения «вероятности» — вероятность получения в результате испытания или наблюдения того или иного числового значения некоторой измеряемой (наблюдаемой) величины. Предполагается, что до проведения испытания (наблюдения) точное значение этой величины неизвестно, то есть имеется явная неопределённость, связанная обычно (за исключением квантовой физики) с невозможностью учёта всех факторов, влияющих на результат. Такие величины называют случайными. В современной теории вероятностей понятие случайной величины формализуется и она определяется как функция «случая» — функция на пространстве элементарных событий. При таком определении наблюдаются не сами элементарные события, а «реализации», конкретные значения случайной величины. Например, при подбрасывании монетки выпадает «решка» или «орел». Если ввести функцию, ставящую в соответствие «решке» — число 1, а «орлу» — 0, то получим случайную величину как функцию указанных исходов. При этом понятие случайной величины обобщается на функции, отображающие пространство элементарных событий в некоторое пространство произвольной природы, соответственно можно ввести понятия случайного вектора, случайного множества и т. д. Однако, обычно под случайной величиной подразумевают именно числовую функцию (величину).
Отвлекаясь от описанной формализации под пространством элементарных событий можно понимать множество возможных значений случайной величины. Сигма-алгеброй подмножеств являются произвольные интервалы на числовой оси, их всевозможные (счётные) объединения и пересечения. Вероятностную меру называют в данном случае распределением случайной величины. Достаточно задать вероятностную меру для интервалов вида 







Распределение случайной величины даёт её полную характеристику. Однако, часто используют отдельные характеристики этого распределения. В первую очередь это математическое ожидание случайной величины — среднее ожидаемое значение случайной величины с учётом взвешивания по вероятностям появления тех или иных значений, и дисперсия или вариация — средний квадрат отклонения случайной величины от её математического ожидания. В некоторых случаях используются и иные характеристики, среди которых важное значение имеют асимметрия и эксцесс. Описанные показатели являются частными случаями так называемых моментов распределения.
Существуют некоторые стандартные законы распределения, часто используемые на практике. В первую очередь — это нормальное распределение (распределение Гаусса). Оно полностью характеризуется двумя параметрами — математическим ожиданием и дисперсией. Его широкое использование связано, в частности, с так называемыми предельными теоремами (см. ниже). При проверке гипотез часто возникают распределения Хи-квадрат, распределение Стьюдента, распределение Фишера. При анализе дискретных случайных величин рассматриваются биномиальное распределение, распределение Пуассона и др. Также часто рассматривается гамма-распределение, частным случаем которого является экспоненциальное распределение, а также указанное выше распределение Хи-квадрат Естественно, используемые на практике распределения не ограничиваются только этими распределениями.
Часто на практике исходя из априорных соображений делается предположение, что распределение вероятностей данной случайной величины относится к некоторому известному с точностью до параметров распределению. Например, к тому же нормальному распределению, но с неизвестным математическим ожиданием и дисперсией (эти два параметра однозначно определяют все нормальное распределение). Задачей статистических наук (математическая статистика, эконометрика и т. д.) в таком случае является оценка значений этих параметров наиболее эффективным (точным) способом. Существуют критерии, с помощью которых можно установить степень «истинности» соответствующих методов оценки. Обычно требуется как минимум состоятельность оценки, несмещённость и эффективность в некотором классе оценок.
На практике применяются также непараметрические методы оценки распределений.
Законы больших чисел[править | править код]
Важнейшее значение в теории вероятностей и в её приложениях имеет группа теорем, объединяемых обычно под названием «закон больших чисел» или предельных теорем. Не прибегая к строгим формулировкам, можно сказать, например, что при некоторых слабых условиях среднее значение независимых одинаково распределенных случайных величин стремится к их математическому ожиданию при достаточно большом количестве этих случайных величин. Если в качестве совокупности случайных величин рассматривать независимые наблюдения одной и той же случайной величины, то это означает, что среднее по выборочным наблюдениям должно стремиться к истинному (неизвестному) математическому ожиданию этой случайной величины. Это закон больших чисел в форме Чебышёва. Это даёт основу для получения соответствующих оценок.
Весьма частным, но очень важным случаем является схема Бернулли — независимые испытания, в результате которых некоторое событие либо происходит, либо нет. Предполагается, что в каждом испытании вероятность наступления события одинакова и равна 






Наряду с указанными теоремами существует так называемая центральная предельная теорема, которая даёт предельное распределение вероятностей для средней, а именно, при определённых слабых условиях среднее значение наблюдений случайной величины при достаточно большом количестве наблюдений имеют нормальное распределение (независимо от исходного распределения самой случайной величины). Например, такое имеет место для среднего значения независимых одинаково распределенных случайных величин. В частности эта теорема применима и к схеме Бернулли. Вообще количество появлений события A в n испытаниях имеет биномиальное распределение, однако при достаточно большом количестве наблюдений это распределение согласно указанной теореме стремится к нормальному распределению в данном случае с математическим ожиданием 







Байесовский подход к вероятности[править | править код]
В основе вышеописанного объективного (частотного) подхода лежит предположение о наличии объективной неопределённости, присущей изучаемым явлениям. В альтернативном байесовском подходе неопределённость трактуется субъективно — как мера нашего незнания. В рамках байесовского подхода под вероятностью понимается степень уверенности в истинности суждения — субъективная вероятность.
Идея байесовского подхода заключается в переходе от априорных знаний к апостерирорным с учётом наблюдаемых явлений. Суть байесовского подхода следует из описанной выше формулы Байеса. Пусть имеются полный набор гипотез 








В частности в отличие от базового подхода к оценке распределений случайных величин, где предполагается, что на основе наблюдений оцениваются значения неизвестных параметров распределений, в байесовском подходе предполагается что параметры — тоже случайные величины (с точки зрения нашего незнания их значений). В качестве гипотез выступают те или иные возможные значения параметров и предполагаются данными некоторые априорные плотности неизвестных параметров 



Вероятность, информация и энтропия[править | править код]
Пусть имеется 




Пусть теперь задана некоторая случайная величина α, распределённая на 



где 
При равновероятных исходах (

Указанную величину называют информацией, информационным количеством, информационной энтропией и т. д. Такое определение информации абстрагируется от какого-либо содержания информации, содержания конкретных исходов. Информационное количество определяется только на основе вероятностей. Величину 
Вероятность и квантовая физика[править | править код]
В квантовой механике состояние системы (частицы) характеризуется волновой функцией (вообще говоря вектором состояния) — комплекснозначной функцией «координат», квадрат модуля которого интерпретируется как плотность вероятности получения заданных значений «координат». Согласно современным представлениям вероятностное определение состояния является полным и причиной вероятностного характера квантовой физики не являются какие-либо «скрытые» факторы — это связано с природой самих процессов. В квантовой физике оказываются возможными любые взаимопревращения различных частиц, не запрещённые теми или иными законами сохранения. И эти взаимопревращения подчиняются закономерностям — вероятностным закономерностям. По современным представлениям принципиально невозможно предсказать ни момент взаимопревращения, ни конкретный результат. Можно лишь говорить о вероятностях тех или иных процессов превращения. Вместо точных классических величин в квантовой физике возможна только оценка средних значений (математических ожиданий) этих величин, например, среднее время жизни частицы.
Вероятность в других сферах[править | править код]
Кроме вопроса о вероятности факта, может возникать, как в области права, так и в области нравственной (при известной этической точке зрения) вопрос о том, насколько вероятно, что данный частный факт составляет нарушение общего закона. Этот вопрос, служащий основным мотивом в религиозной юриспруденции Талмуда, вызвал и в римско-католическом нравственном богословии (особенно с конца XVI века) весьма сложные систематические построения и огромную литературу, догматическую и полемическую (см. Пробабилизм)[1].
См. также[править | править код]
- Вероятность перехода
- Измерение (квантовая механика)
- Квантовая вероятность
- Мера множества
- Метод Монте-Карло
- Принцип неопределённости
- Риск
- Случайная величина
- Случайность
- Условная вероятность
- Формула Бернулли
- Формула полной вероятности
Примечания[править | править код]
- ↑ 1 2 3 В. С. Соловьёв Вероятность // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Так, например, в юриспруденции, когда подлежащий суду факт устанавливается на основании свидетельских показаний, он всегда остаётся, строго говоря, лишь вероятным, и необходимо знать, насколько эта вероятность значительна. В римском праве здесь принималось четверное деление: probatio plena (где вероятность практически переходит в достоверность), далее — probatio minus plena, затем — probatio semiplena major и, наконец, probatio semiplena minor. В римском языке слово вероятность этимологически родственно слову честность.
- ↑ 1 2 Гнеденко Б. В. Курс теории вероятностей: Учебник — Изд. 6-е, перераб. и доп. — М.: Наука. Гл. ред. физ. мат. лит., 1988 — 448с.- с.386-387
- ↑ Abrams, William, A Brief History of Probability, Second Moment, <http://www.secondmoment.org/articles/probability.php>. Проверено 10 ноября 2017. Архивная копия от 24 июля 2017 на Wayback Machine
- ↑ Григорян А. А. Теория вероятностей Р. фон Мизеса: история и философско-методологические основания // Историко-математические исследования. — М.: Янус-К, 1999. — № 38 (4). — С. 198—220.
- ↑ Математика XIX века. Том I, 1978, с. 238—239.
- ↑ Гнеденко Б. В., 2005, с. 407—408.
- ↑ Математика XIX века. Том I, 1978, с. 240.
- ↑ Алимов Ю. И., Кравцов Ю. А. Является ли вероятность «нормальной» физической величиной? // Успехи физических наук. — М., 1992. — № 162 (7). — С. 149—182. Архивировано 20 октября 2020 года.
- ↑ Тутубалин В. Н. Вероятность, компьютеры и обработка результатов эксперимента // Успехи физических наук. — М., 1993. — № 163 (7). — С. 93—109. Архивировано 21 января 2021 года.
- ↑ Точнее предполагается, что мера определена как минимум на некотором полукольце подмножеств и далее доказывается, что она в таком случае определена и на минимальном кольце, содержащем это полукольцо и более того, эту меру можно продолжить на сигма-алгебру подмножеств
Литература[править | править код]
- Альфред Реньи. Письма о вероятности / Пер. с венг. Д. Сааса и А. Крамли под ред. Б. В. Гнеденко. — М.: Мир, 1970.
- Вероятность в физике // Энциклопедический словарь юного физика / В. А. Чуянов (сост.). — М.: Педагогика, 1984. — С. 39. — 352 с.
- Гнеденко Б. В. Курс теории вероятностей. — М., 2007. — 42 с.
- Гнеденко Б. В. Очерк по истории теории вероятностей // Курс теории вероятностей. 8-е изд. — Μ.: Едиториал УРСС, 2005. — 448 с. — ISBN 5-354-01091-8. — С. 366—435.
- Купцов В. И. Детерминизм и вероятность. — М., 1976. — 256 с.
- Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. Том I / Под ред. А. Н. Колмогорова, А. П. Юшкевича. — М.: Наука, 1978. — 255 с.
Содержание:
В статистике наиболее часто применяются такие распределения:
- Нормальное (Гауссовское) распределение.
- Распределение Пирсона, распределение
- Распределение Стьюдента (t – распределение).
- Распределение Фишера (F – распределение).
Нормальный закон распределения мы подробно рассмотрели при изучении раздела 6.5 теории вероятностей и здесь рассматриваться не будет.
Отметим, что в законы распределений математической статистики входит гамма-функция, поэтому необходимо познакомиться с этой функцией и рассмотреть ее свойства.
Гамма-функция и ее свойства
Гамма-функцией или интегралом Эйлера второго рода называется функция следующего вида:
где 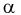
Свойства гамма-функции:
1. Г(1) = Г(2) = 1.
Доказательство:
Подставим
2.
Доказательство:
Вычислим интеграл в (9.1), используя интегрирование по частям:
Доказательство:
Значит, если значение 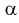
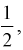
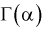
Для целых 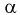
Например,
Г(3) = 2! = 2, Г(4) = 3! = 6, Г(5) = 4! = 24.
Отметим, что смысл гамма-функции – распространение понятия факториал на нецелые значения. На рис. 9.1 приведен график гамма-функции.
Распределение (хи-квадрат )
Распределение 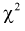
Случайная величина имеет закон распределения 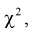
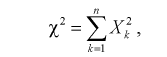
где 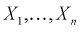
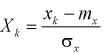
Распределение случайной величины, определенной по формуле (9.2), называется распределением Пирсона.
Покажем, что плотность распределения случайной величины 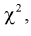
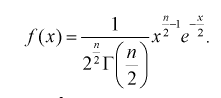
Здесь для краткости записи
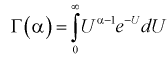
Для доказательства используем аппарат характеристических функций. Найдем характеристическую функцию случайной величины которая входит в формулу (9.2), учитывая, что 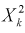
Используем подстановку 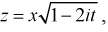
Согласно 5-му свойству характеристической функции (для суммы независимых случайных величин) найдем характеристическую функцию 
Найдем характеристическую функцию 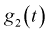
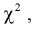
При сравнении правых частей характеристических функций 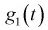
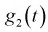
Найдем математическое ожидание и дисперсию случайной величины
Продифференцируем 2 раза
Значения производных при t = 0:
Таким образом, математическое ожидание 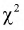
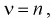
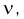
С ростом 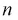
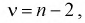
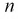
При 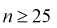
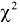
Квантилем 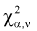
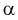
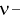
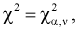
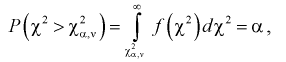
т. е. это то значение 
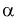
Распределение Стьюдента
Распределение Стьюдента 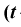
Случайная величина t имеет распределение Стьюдента, если она определяется так.
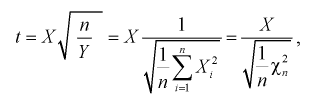
где X – нормированная нормальная случайная величина,
Y – величина 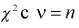
X и Y – независимые случайные величины.
Случайная величина t является функцией нормально распределенных нормированных случайных величин и называется безразмерной дробью Стьюдента. Плотность распределения случайной величины t определяется равенством
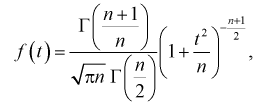
где
Числовые характеристики случайной величины t :
На рис. 9.3 приведены кривые распределения Стьюдента. Кривые на рис. 9.3 качественно напоминают кривые нормального закона распределения с математическим ожиданием, равным нулю, и при 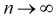
Квантили распределения Стьюдента 
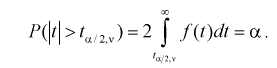
Рис. 9.4 иллюстрирует процесе определения квантилей, т. е. необходимо так выбрать 
Распределение Фишера (F-распределение)
Случайная величина F имеет распределение Фишера, если она определяется так:
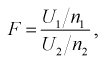
где 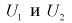
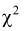
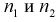
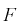
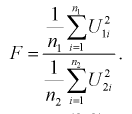
Безразмерная случайная величина F (9.8) имеет плотность распределения, определяемую следующей формулой:
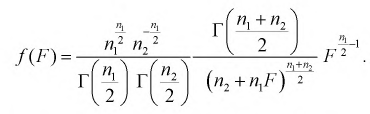
Распределение случайной величины F зависит от двух параметров 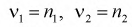
Квантили распределения Фишера 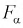
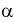
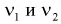
На рис. 9.6 показано, что надо так выбрать 
Как правило, квантили 
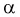
Биноминальный закон распределения
Определение: Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями 
Как видим, вероятности Р(Х = m) находятся по формуле Бернулли.
Следовательно, биноминальный закон распределения представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биноминального закона имеет вид:
Теорема. Математическое ожидание случайной величины, распределенной по биноминальному закону 
Следствие. Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью, равно 
Биноминальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Закон распределения Пуассона
Определение: Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m с вероятностями 
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.
При достаточно больших n (вообще при n → ∞) и малых значениях р (р → 0) при условии, что произведение np – постоянная величина (nр → λ = const), закон распределения Пуассона является хорошим приближением биноминального закона. Т.е. при n → ∞, р → 0, nр → λ = const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона часто называют законом редких явлений.
По закону Пуассона распределены, например, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание в единицу времени в системах массового обслуживания, и т.п.
Отметим еще, что если случайная величина представляет собой сумму двух независимых случайных величин, каждая из которых распределена по закону Пуассона, то она также распределена по закону Пуассона с параметром
Равномерный закон распределения
Определение: Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности f(x) постоянна на этом отрезке и равна нулю вне его, т.е.
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.1 и рис. 7.2.
Теорема. Функция распределения случайной величины Х, распределенной по равномерному закону, есть
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач теории массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению, и т.д.
Показательный (экспоненциальный) закон распределения
Определение: Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности f(x) имеет вид:
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.3 и рис. 7.4.
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть 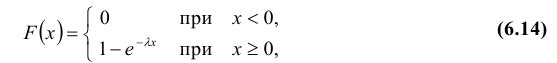

Отсюда следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е.
Вероятность попадания в интервал [a; b] непрерывной случайной величины Х, распределенной по показательному закону, находится как
Пример:
Установлено, что время ремонта железнодорожных вагонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт вагона потребуется менее 7 дней, если среднее время ремонта вагонов составляет 10 дней.
Решение:
По условию математическое ожидание М(Х) = 1/λ = 10, откуда параметр λ = 0,1. По формуле (6.17) находим вероятность попадания случайной величины Х в интервал [0, 7]:
Показательный закон распределения играет большую роль в теории массового обслуживания. Так например, интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока. Кроме того, показательное распределение широко применяется в теории надежности, одним из основных понятий которой является функция надежности.
Функция надежности
Будем называть элементом некоторое устройство. Пусть элемент начинает работать в момент времени 
Таким образом, интегральная функция 
Функцией надежности R(τ), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью τ: 
Широкое использование показательного закона распределения обусловлено тем, что только он обладает следующим важным свойством: Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части 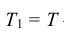
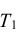
Пример:
Время безотказной работы устройства распределено по показательному закону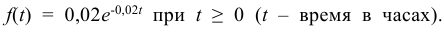
Решение:
По условию постоянная интенсивность отказов λ = 0,02. Используя формулу (6.18), получаем:
Нормальный закон распределения
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Определение: Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 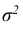
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 6.5 а), б) показана нормальная кривая с параметрами а и 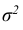
Обратим внимание на то, что нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 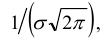
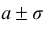
Можно заметить, что в выражении плотности нормального закона параметры распределения обозначены буквами а и 
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру a этого распределения, т.е. 
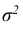
Выясним, как будет меняться нормальная кривая при изменении параметров а и σ. Если σ = const, и меняется параметр a (а1 < а2 < а3), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 6.6).
Если а = const и меняется параметр σ, то меняется ордината максимума кривой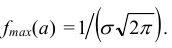
Таким образом, параметр a характеризует положение , а параметр σ – форму нормальной кривой.
Нормальный закон распределения случайной величины с параметрами a = 0 и σ = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции нормального распределения не выражается через элементарные функции. Однако его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения
Такую функцию называют функцией Лапласа, для нее составлены таблицы. Существует много разновидностей такой функции, например:
Мы будем использовать функцию:
Для такой функции табличные значения приведены в Приложении 2.
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле
Рассмотрим свойства случайной величины, распределенной по нормальному закону.
1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [α, β] равна
2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания a не превысит величину δ > 0 (по абсолютной величине), равна
Вычислим по этой формуле вероятности 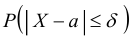
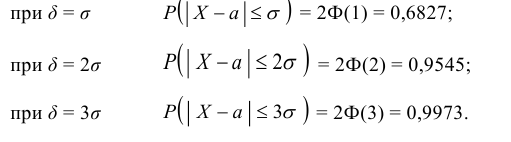
Пример:
Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а = 173 и 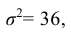
Решение:
1. Находим плотность вероятности 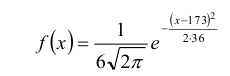
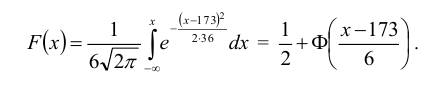
По таблице значений функции Лапласа (Приложение 2) находим:
Окончательно получаем
Долю костюмов 3-го роста (170 – 176 см) можно найти аналогично. Однако проще это сделать, если учесть, что данный интервал симметричен относительно математического ожидания а = 173, т.е. неравенство 170 ≤ Х ≤ 176 равносильно неравенству │Х – 173│≤ 3. Тогда
3. Сформулируем «правило трех сигм» для случайной величины Х: Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Ковариация в теории вероятности
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Нормальный закон распределения















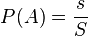
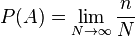
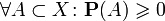 ,
,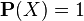 ,
,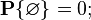

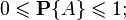


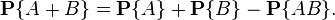
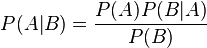
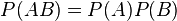
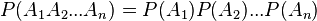
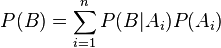
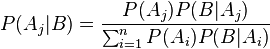
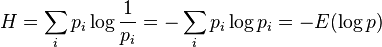




















![{displaystyle H(alpha )=sum _{i}p_{i}log _{2}{frac {1}{p_{i}}}=-sum _{i}p_{i}log _{2}p_{i}=-mathop {mathbb {E} } limits _{agets alpha }[log _{2}Pr(alpha =a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4dd7ac00c86339baceaf161f943a211c09d12c0)