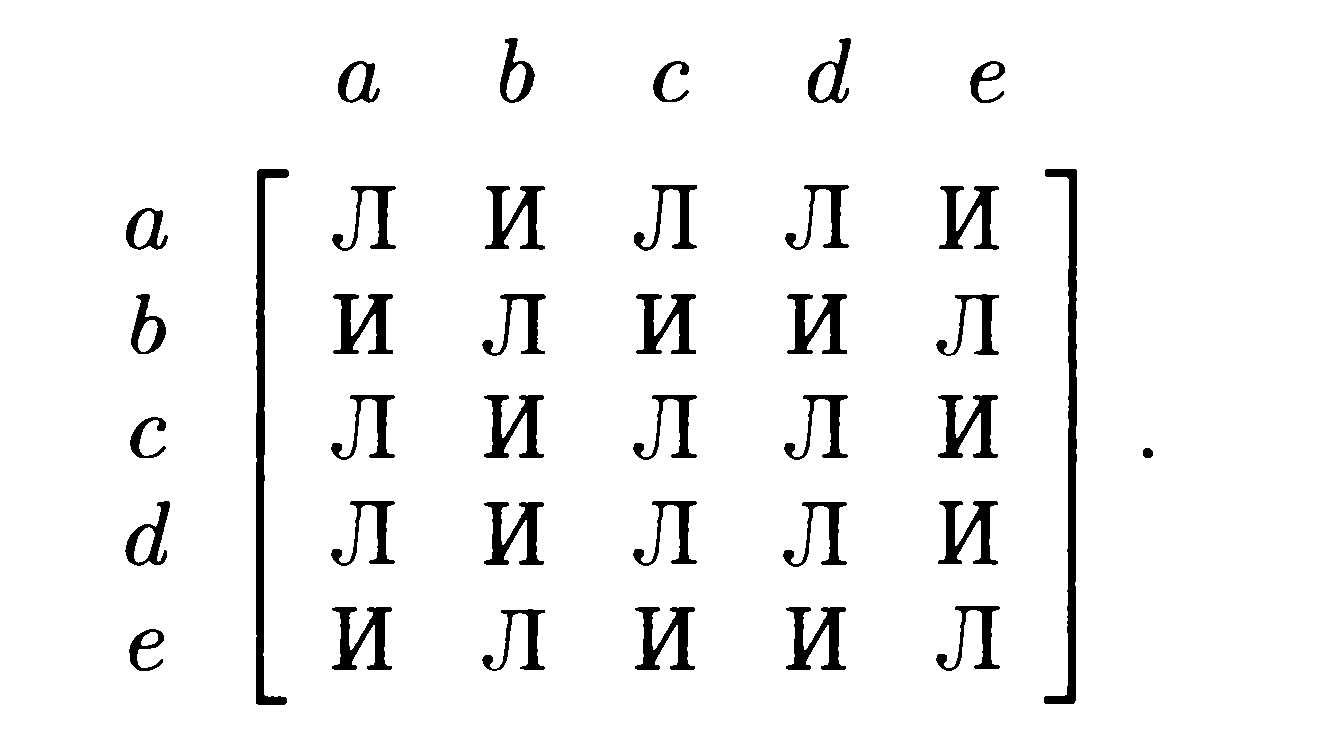Как найти степень вершины неориентированного графа

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июня 2021 года; проверки требуют 3 правки.

Степень (валентность) вершины графа — количество рёбер графа , инцидентных вершине .
При подсчёте степени ребро-петля учитывается дважды.^[1]

Степень вершины обычно обозначается как или .
Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G).
На рис. 1 максимальная степень равна 5, минимальная — 0.
В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.

Лемма о рукопожатиях[править | править код]

По формуле суммы степеней для графа ,

то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, из формулы следует, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других, чётно.

Последовательность степеней вершин[править | править код]

Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью.^[2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристикой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.

Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.

Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность d_i (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство

Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, но не при k равном 2 или 3.

Согласно критерию Гавела — Хакими, если невозрастающая последовательность (d₁, d₂, …, d_n) это последовательность степеней простого графа, то (d₂ − 1, d₃ − 1, …, d_d1+1 − 1, d_d1+2, d_d1+3, …, d_n) некоторая последовательность степеней простого графа. Этот факт позволяет построить полиномиальный алгоритм нахождения простого графа с заданной реализуемой последовательностью.

Сопоставим исходной последовательности чисел вершины графа без ребер с требуемыми степенями. Указанное преобразование последовательностей задает как минимум одну вершину графа, все инцидентные ей ребра и множество вершин с новыми требуемыми дополнениями степеней. Упорядочивая оставшиеся вершины по невозрастанию дополнений степеней, получим невозрастающую последовательность степеней простого графа. Повторяя преобразование и упорядочение не более n-1 раза, получаем весь граф.

Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.

Частные значения[править | править код]

• Вершина степени 0 называется изолированной.
• Вершина степени 1 называется концевой (англ. end vertex), висячей (англ. pendant vertex) или листом графа (англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим (англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных.
• Вершина степени n-1 графа порядка n называется доминирующей (англ. dominating vertex).

Общие свойства[править | править код]

• Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
• Эйлеров путь существует в неориентированном, связном графе тогда и только тогда, когда граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
• Орграф является псевдолесом^{[неизвестный термин]} только если полустепень исхода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени исхода всех вершин равны 1.
• Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
• k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.

См. также[править | править код]

• Полустепень захода и полустепень исхода вершин ориентированных графов
• Распределение степеней

Примечания[править | править код]

Источники[править | править код]

• Дистель, Рейнхард (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, <http://diestel-graph-theory.com/index.html>.
• Эрдёш, П. & Галлаи, T. (1960), Gráfok előírt fokszámú pontokkal, Matematikai Lapok Т. 11: 264—274, <http://www.renyi.hu/~p_erdos/1961-05.pdf>.
• Хакими, С. Л. (1962), On realizability of a set of integers as degrees of the vertices of a linear graph. I, Journal of the Society for Industrial and Applied Mathematics Т. 10: 496–506.
• Сирксма, Хирард & Хоохефен, Хан (1991), Seven criteria for integer sequences being graphic, Journal of Graph Theory Т. 15 (2): 223–231, DOI 10.1002/jgt.3190150209.

Определение
7.10. Степенью
вершины v
для неориентированного графа, обозначается
d(v),
называется количество ребер, инцидентных
этой вершине. Вершина степени 0 называется
изолированной.
Вершина степени 1 называется висячей.

Определение
7.11. Полустепенью
исхода вершины
v
для орграфа
называется количество дуг, для которых
v
является начальной вершиной, обозначается
.

Полустепенью
захода
вершины v
называется количество дуг, для которых
v
является конечной вершиной, обозначается
.
Если,
то вершинаv
называется истоком.
Если
,
то вершинаv
называется стоком.

Теорема 7.2.
(Теорема
Эйлера)
Сумма степеней вершин графа равна
удвоенному количеству ребер:

.

Доказательство.
При подсчете суммы степеней вершин
каждое ребро учитывается два раза: для
одного конца ребра и для другого.

Следствие 1.
Число вершин нечетной степени четно.

Доказательство.
По теореме Эйлера сумма степеней всех
вершин – четное число. Сумма степеней
вершин четной степени четна, значит,
сумма степеней вершин нечетной степени
также четна, следовательно, их четное
число.

Следствие 2.
Сумма полустепеней вершин орграфа
равна удвоенному количеству дуг:

.

Доказательство.
Сумма полустепеней вершин орграфа
равна сумме степеней вершин графа,
полученного из орграфа забыванием
ориентации дуг.

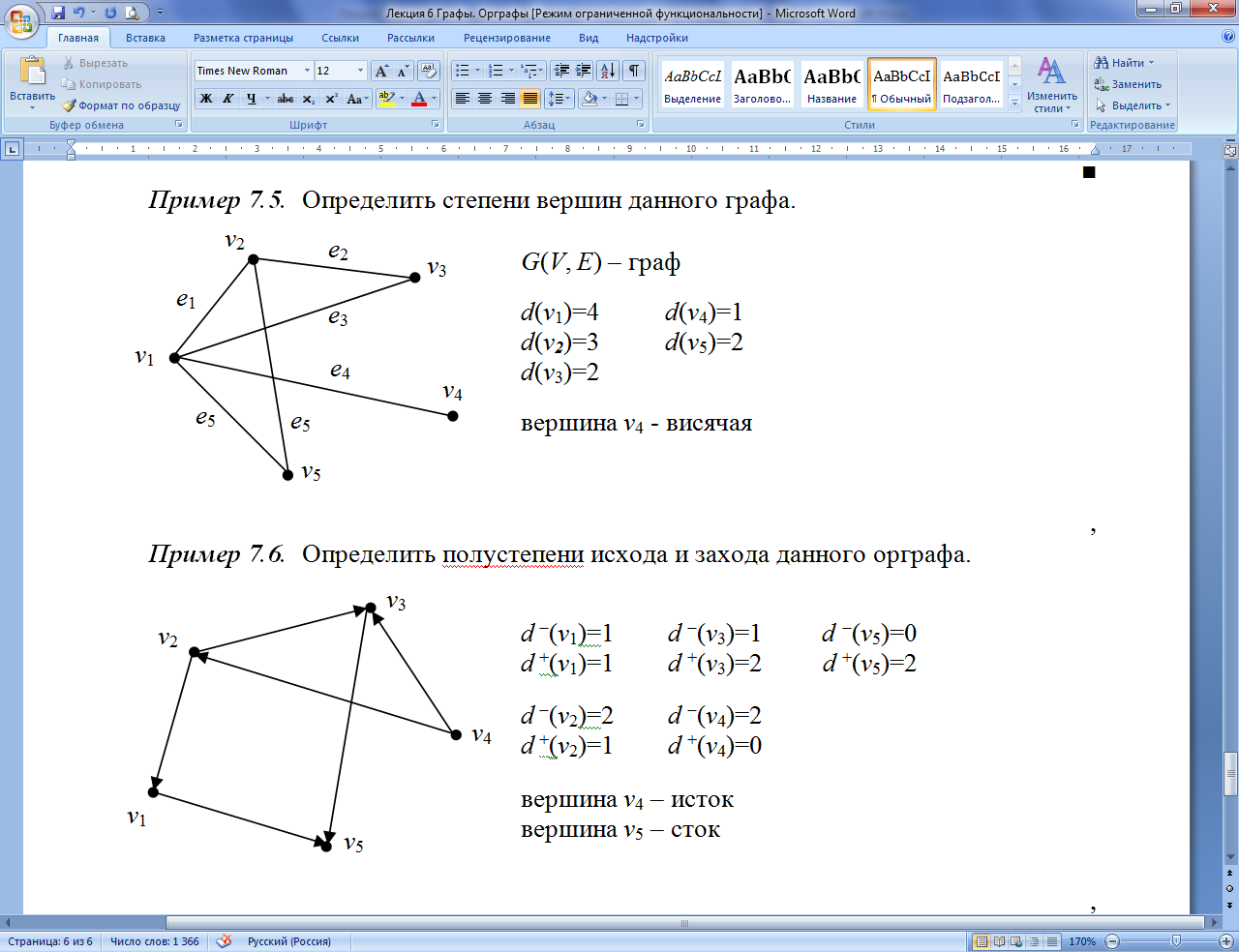
Пример 7.5.
Определить степени вершин данного
графа.

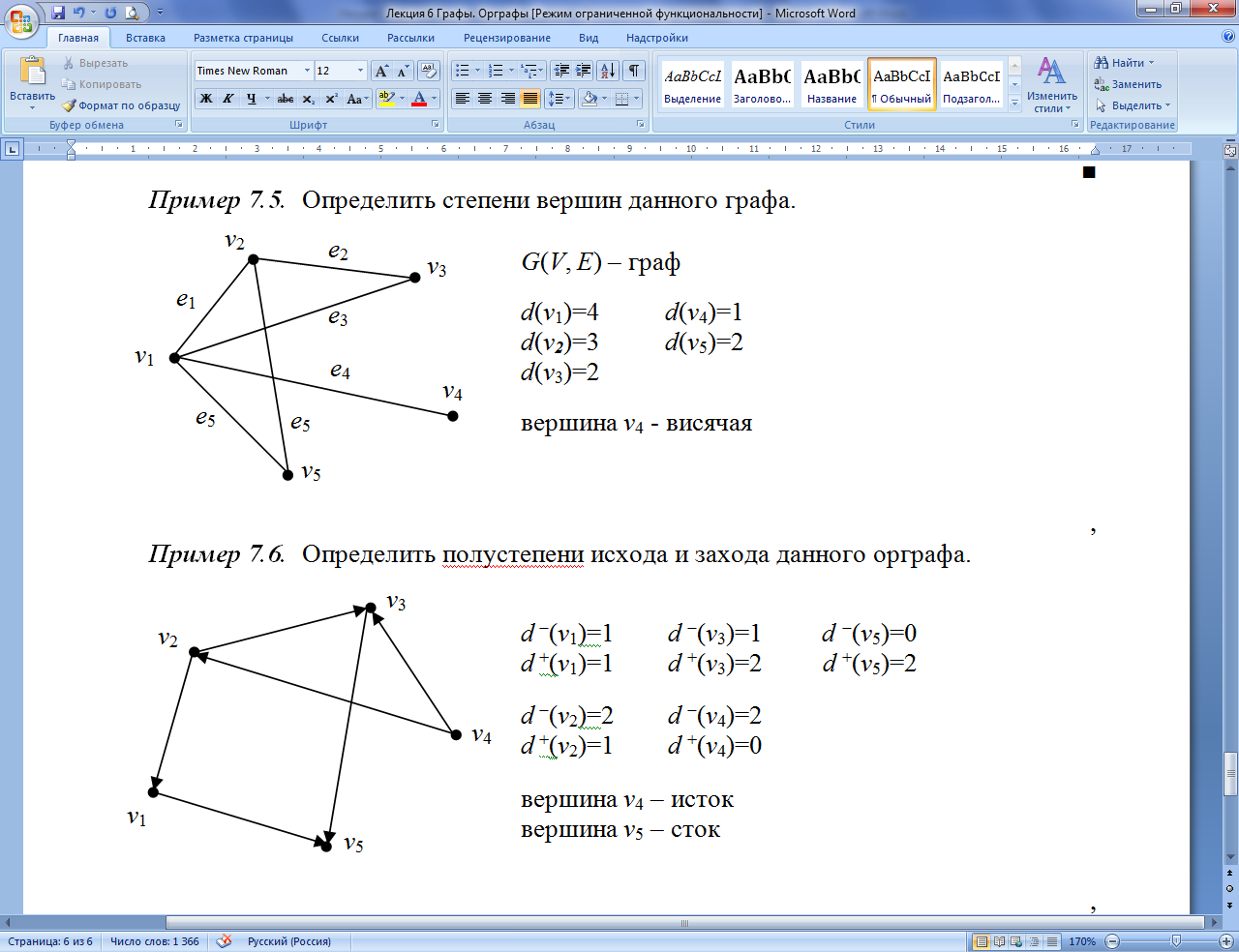
Пример 7.6.
Определить полустепени исхода и захода
данного орграфа.

7.5. Представление (способы задания) графов.

1. Граф
   как алгебраическая система:

модель, носителем
которой является множество вершин, а
отношение – бинарное отношение смежности
вершин.

< {a,b,c,d};
– множество
вершин

{(a,b),(b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}
– множество
рёбер
>

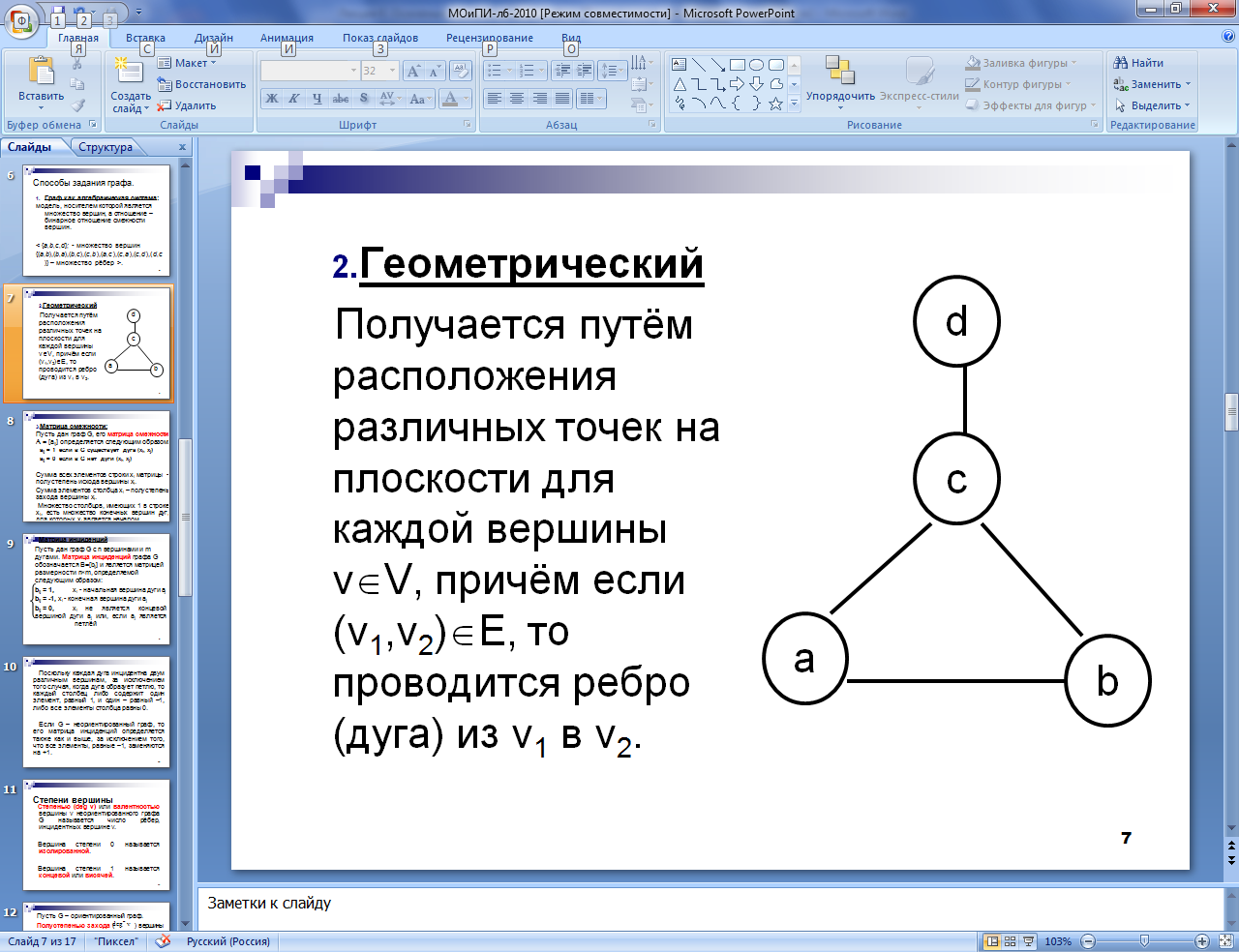
1. Геометрический

Получается путём
расположения различных точек на
плоскости для каждой вершины vÎV,
причём если (v₁,v₂)ÎЕ,
то проводится ребро (дуга) из v₁
в v₂.

Для представления
в компьютере чаще всего граф задается
либо матрицей
смежности,
либо матрицей
инциденций.

Матрицей
смежности вершин неориентированного
графа
G,
содержащего n
вершин, называют квадратную матрицу
A=a_ij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам
неориентированного графа.

Элементы a_ij
матрицы A
равны числу ребер, направленных из i-й
вершины в j-ю.
В случае неориентированного
графа G
ему вместе с ребром (v_i,
v_j)
принадлежит и ребро (v_j,
v_i),
поэтому матрица смежности вершин
A=a_ij
будет симметрична относительно главной
диагонали.

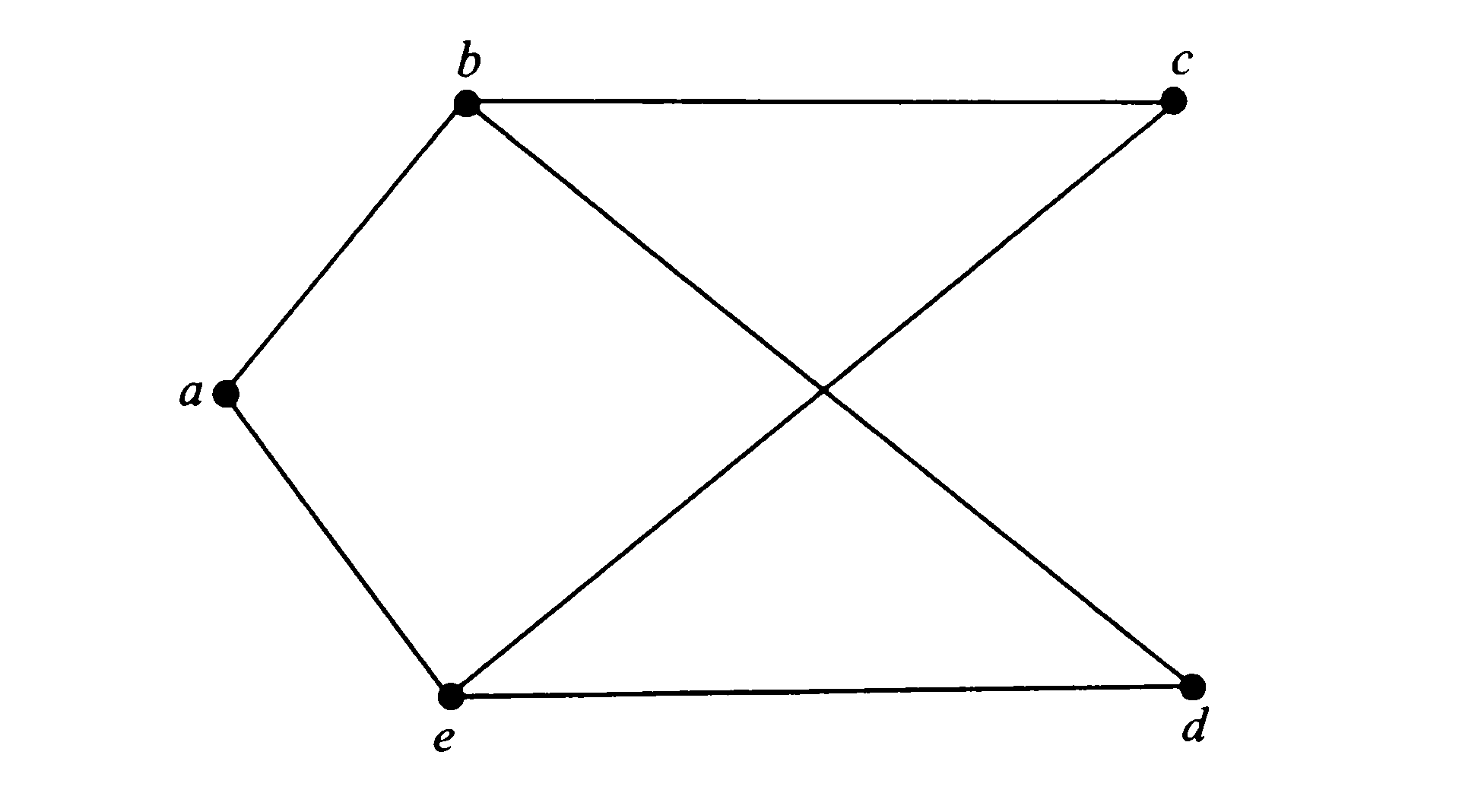
ПРИМЕР.
Граф: множество вершин V
= {a,b,c,d,e}

Множество
ребер

Е
= {{а, b},
{а, е}, {b,
c},
{b,
d},
{c,
e},
{d,e}},

Матрица смежности
симметрична относительно главной
диагонали.

На главной диагонали
стоит 1 (символ Л) из-за
нерефлексивности
отношения на множестве вершин (EÍV´V)

Логическая матрица
отношения на множестве вершин графа,
которое задается его ребрами.

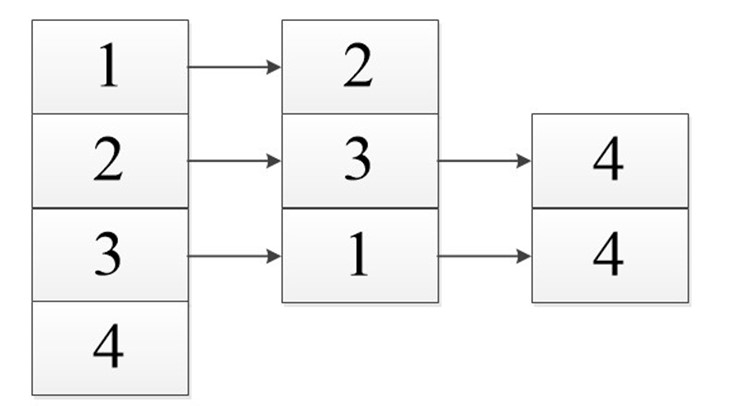
a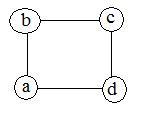 b c d

a 0 1 0 1

b 1 0 1 1

с 0 1 0 1

d 1 1 1 0

простой
граф

a b c d

a 1 1 0 1

b 1 0 3 0

c 0 3 0 2

d 1 0 2 0

граф
с кратными

рёбрами
и петлёй

Определение
7.12. Матрица
смежности вершин орграфа
G,
содержащего n
вершин-
это квадратная матрица A=a_ij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам орграфа.

Элементы a_ij
матрицы A
равны числу дуг, направленных из i-й
вершины в j-ю.
Если орграф состоит из однократных
дуг, то элементы матрицы равны либо 0,
либо 1.

Матрица
смежности:

Пусть дан граф G,
его матрица
смежности
А = [a_ij]
определяется следующим образом:

a_ij
= 1 если в G
существует дуга (x_i,
x_j)

a_ij
= 0 если в G
нет дуги (x_i,
x_j)

Определение
7.14. Матрицей
инциденций (инцидентности) неориентированного
графа с
вершинами
и
ребрами
называется
матрица
размерности,
строки которой соответствуют вершинам,
а столбцы – ребрам. Элементыматрицы инциденций неориентированного
графа равны 1, если вершинаинцидентна ребру,
и 0 в противном случае.

Матрицей
инциденций (инцидентности) орграфа с
вершинами
и
дугами
называется
матрица
размерностиnm,
строки которой соответствуют вершинам,
а столбцы -дугам
орграфа.

Элементы c_ij
равны

1, если дуга e_j
исходит из i-й
вершины;

–1, если дуга e_j
заходит в i-ю
вершину;

0, если дуга не
инцидентна i-й
вершине

Поскольку каждая
дуга инцидентна двум различным вершинам,
за исключением того случая, когда дуга
образует петлю, то каждый столбец либо
содержит один элемент, равный 1, и один
– равный –1, либо все элементы столбца
равны 0.

Степень вершины
равна сумме элементов строки, обозначенной
этой вершиной, так как каждая единица
в этой строке представляет инцидентность
этой вершины ребру.

В каждом столбце
также будут две единицы, так как каждое
ребро инцидентно двум вершинам.

Матрицы инцидентности
не имеют большого значения при
рассмотрении ориентированных графов,
т.к. они не содержат информации о том,
как ребро ориентировано.

Поэтому, используя
матрицу инцидентности, нельзя восстановить
ориентированный граф.

Такую возможность
обеспечивает матрица смежности,

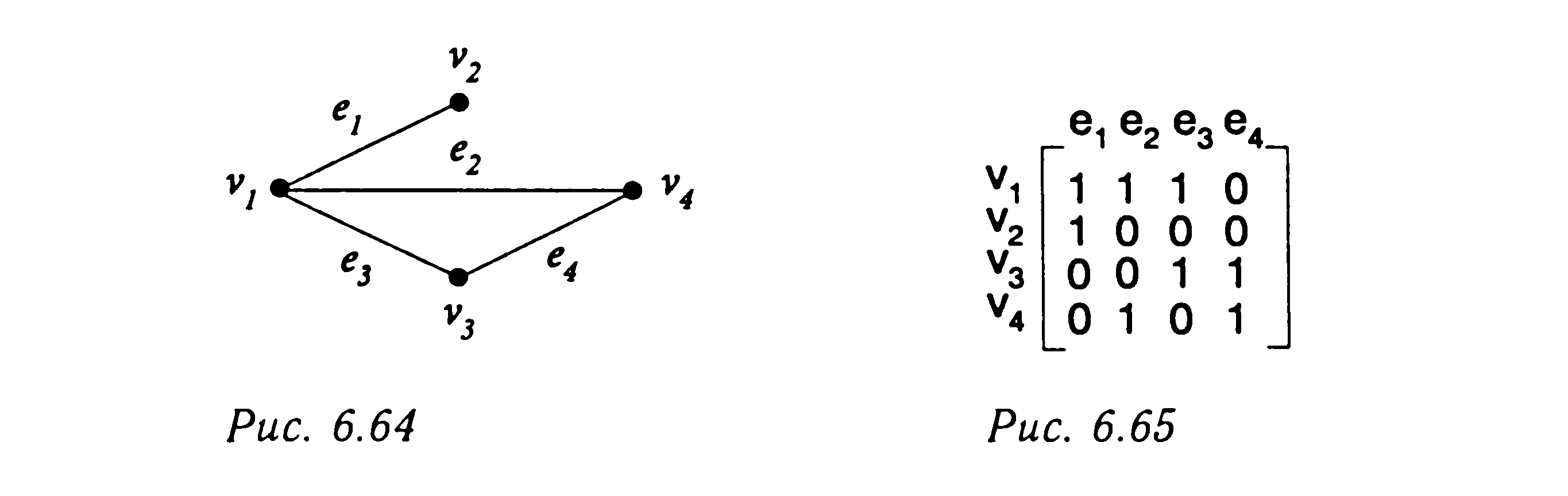
Пример
7.7.1.
Для заданного неориентированного
графа построить матрицы смежностей и
матрицу инциденций.

Решение.
1) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

2) Строим матрицу
инциденций, которая будет размерности
45.

Пример
7.7.2.
Для заданного ориентированного графа
построить матрицы смежностей и матрицу
инциденций.

Решение.
1) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

2) Строим матрицу
инциденций, которая будет размерности
45.

График – это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.

точка

Точка – это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.

пример

Здесь точка – это точка с именем «а».

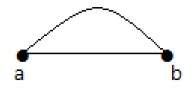
Линия

Линия – это связь между двумя точками. Это может быть представлено сплошной линией.

пример

Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.

темя

Вершина – это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.

пример

Здесь вершина названа с алфавитом «а».

край

Ребро – это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.

пример

Здесь «a» и «b» – две вершины, и связь между ними называется ребром.

график

Граф ‘G’ определяется как G = (V, E), где V – множество всех вершин, а E – множество всех ребер графа.

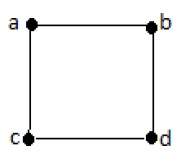
Пример 1

В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.

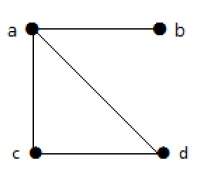
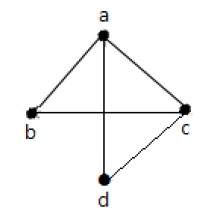
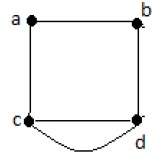
Пример 2

В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.

петля

В графе, если ребро нарисовано от вершины к себе, это называется циклом.

Пример 1

На приведенном выше графике V – вершина, для которой у нее есть ребро (V, V), образующее петлю.

Пример 2

В этом графе есть две петли, которые сформированы в вершине a, и вершине b.

Степень вершины

Это число вершин, смежных с вершиной V.

Обозначение – град (V).

В простом графе с n числом вершин степень любых вершин равна –

deg(v) ≤ n – 1 ∀ v ∈ G

Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.

Степень вершины можно рассматривать по двум случаям графов –

• Ненаправленный граф
• Направленный граф

Степень вершины в неориентированном графе

Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.

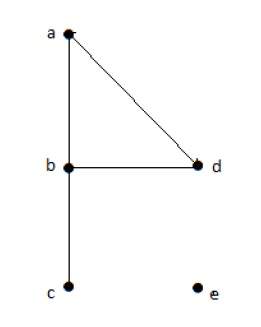
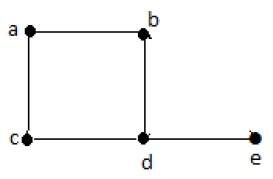
Пример 1

Посмотрите на следующий график –

На приведенном выше неориентированном графике

• deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

• deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

• deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

  Итак, «c» – это вершина с кулоном .

• deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

• deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

  Так что «е» – изолированная вершина .

deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.

deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.

deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро

Итак, «c» – это вершина с кулоном .

deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.

deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.

Так что «е» – изолированная вершина .

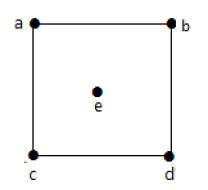
Пример 2

Посмотрите на следующий график –

На приведенном выше графике

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.

Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.

Степень вершины в ориентированном графе

В ориентированном графе каждая вершина имеет степень и степень.

Степень графа

• Степень вершины V – это количество ребер, входящих в вершину V.

• Обозначение – град ^– (V).

Степень вершины V – это количество ребер, входящих в вершину V.

Обозначение – град ^– (V).

Степень графа

• Отступ вершины V – это число ребер, выходящих из вершины V.

• Обозначение – град ⁺ (V).

Отступ вершины V – это число ребер, выходящих из вершины V.

Обозначение – град ⁺ (V).

Рассмотрим следующие примеры.

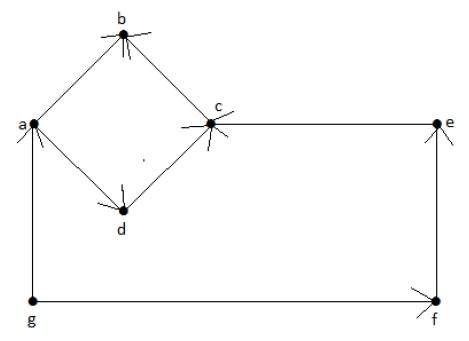
Пример 1

Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
	1	2
б	2	0
с	2	1
d	1	1
е	1	1
е	1	1
г	0	2

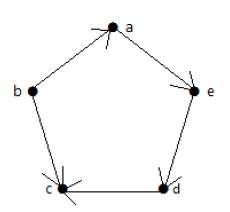
Пример 2

Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.

Степень и степень других вершин показаны в следующей таблице:

темя	полустепень захода	полустепень
	1	1
б	0	2
с	2	0
d	1	1
е	1	1

Кулон Вертекс

Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.

пример

Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.

Изолированная вершина

Вершина с нулевой степенью называется изолированной вершиной.

пример

Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.

смежность

Вот нормы смежности –

• В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.

• В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.

В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.

Пример 1

На приведенном выше графике –

• «a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».

• «a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

• ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

• be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

«a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».

«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».

ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.

be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.

Пример 2

На приведенном выше графике –

• a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

• ‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

• ‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

• ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.

‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.

‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.

ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.

Параллельные края

В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.

На приведенном выше графике «a» и «b» – это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.

Мульти График

Граф, имеющий параллельные ребра, называется мультиграфом.

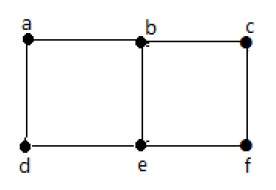
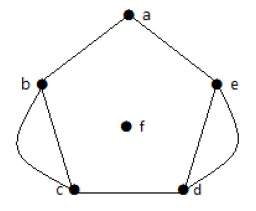
Пример 1

На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.

Пример 2

На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.

Степень последовательности графика

Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.

Пример 1

темя		б	с	d	е
Присоединенный к	До нашей эры	объявление	объявление	с, Ь, е	d
степень	2	2	2	3	1

На приведенном выше графике для вершин {d, a, b, c, e} последовательность степеней равна {3, 2, 2, 2, 1}.

Пример 2

темя		б	с	d	е	е
Присоединенный к	быть	а, с	б, г	с, е	объявление	–
степень	2	2	2	2	2	0

На приведенном выше графике для вершин {a, b, c, d, e, f} последовательность степеней равна {2, 2, 2, 2, 2, 0}.

Обо мне

Меня зовут Елена, и я занимаюсь подготовкой школьников к ЕГЭ 8 лет. В 2010 году я сдавала ЕГЭ по информатике для поступления (сдавала информатику, когда это еще не было мейнстримом)). Тогда основная часть экзамена была очень легкой: по моим ощущениям, на уровне современного ОГЭ. За 12 лет КИМы сильно усложнились, но я считаю это плюсом – теперь экзамен соответствует формату вступительного для вуза.

Мне нравится заниматься со школьниками информатикой, решать интересные (=сложные) задачи, рассказывать какие-то лайфхаки и слышать «ух ты, а так можно было?».

На этом канале я планирую рассказывать, как решать задачи базового и повышенного уровня. Надеюсь на вашу обратную связь – понятно ли объяснение, получается ли решать задачи из ДЗ. Также приветствую предложения разобрать какое-то конкретное задание.

О задании 1 типа из ЕГЭ по информатике

В данный момент на экзамене представлены задачи, в которых требуется уметь работать с информационными моделями, изображающими схему дорог между населенными пунктами. Несмотря на разные формулировки вопросов, задания можно разбить на две группы. Для получения ответа в задачах из первой группы нужно найти полное или частичное соответствие между графом и таблицей. В задачах второй группы предлагается найти кратчайший (или самый длинный) маршрут между двумя пунктами, опираясь на информационную модель в виде графа или таблицы. Строго говоря, существуют задачи и со смешанными формулировками.

В рамках этой статьи:

• рассмотрим кусочек теории графов (да простит меня мой преподаватель по дискретной математике!), который понадобится для решения задач формата ЕГЭ по информатике. Сразу оговорюсь, что теорию я объясняю больше «на пальцах», чем в академическом формате;
• порешаем задачи из ЕГЭ с двух источников (рассмотрим только задачи на соответствие между графом и таблицей);
• в конце я приведу список задач для самостоятельной отработки.

Немного теории

Что такое граф?

Граф – это геометрическая фигура, состоящая из точек, называемых вершинами, соединенных отрезками – ребрами графа. Для облегчения восприятия можно думать о графе как о городах, соединенных дорогами.

Графы бывают ориентированными и неориентированными (их еще называют направленными и ненаправленными). Ориентированные графы – те, ребра которых имеют направление (оно указывается стрелкой). По таким ребрам можно перемещаться только в одну сторону. Неориентированные графы – те, ребра которых не имеют направления (см. рис. 1).

В рамках первого задания будем рассматривать неориентированные графы.

Соответствие между графом и таблицей

В соответствие графу можно поставить таблицу. Для этого пронумеруем вершины графа с рис. 1(б) буквами. У нас получилось пять вершин (от А до Д).

Теперь построим таблицу, соответствующую нашему графу. Она будет иметь следующий вид:

Ячейки, стоящие на пересечении строк и столбцов, обозначают соответствующие ребра графа. В нашем примере есть ребро АБ (отрезок, соединяющий вершины А и Б). Отметим ячейки таблицы, соответствующие этому ребру, символом «*». Таких ячеек две, так как граф неориентированный, и мы можем передвигаться как из А в Б, так и из Б в А.

Теперь заметим, что нет ребер, соответствующих ячейкам, стоящим на диагонали таблицы (нет ребра АА, ББ и т.д.). Такие ячейки принято заштриховывать:

Отметим в таблице остальные ребра. Заметим, что заштрихованная диагональ является осью симметрии всей таблицы (верхняя половина таблицы симметрична нижней относительно диагонали). Это признак соответствия таблицы неориентированному графу.

Примечание: подобную (но несимметричную) таблицу можно построить и для ориентированного графа.

Посмотрим еще раз на изначальный граф и построенную таблицу. Нужно понимать, что и то, и другое – информационная модель, построенная для одной и той же сети дорог между населенными пунктами. Эти модели равнозначны: все данные, которые можно получить из графа (например, со сколькими пунктами связан пункт А), можно получить и из таблицы.

Степень вершины графа

Дадим нестрогое определение понятию, полезному при решении задач.

Число дорог, выходящих из вершины А неориентированного графа, будем называть степенью вершины А. Степень вершины может быть нулевой, если к этой вершине не ведут дороги, или равной натуральному числу.

Примеры на определение степеней вершин

Пример 1.

Рассмотрим граф на рис. 3 и определим степени для каждой его вершины.

Из вершины А выходит (или входит) две дороги – это вершина степени 2.

Вершина Б – степень 1.

Вершина В – степень 3.

Вершина Г – степень 2.

Вершина Д – степень 0.

Также степени можно определить по таблице. Если данные представлены в табличном виде, мы не можем говорить о степени вершины, так как вершины относятся к графам. Будем эти значения неакадемично называть степенями пунктов.

Пример 2.

В таблице приведены данные о дорогах между населенными пунктами. Найдем степени для каждого пункта.

Чтобы найти степень конкретного пункта, нужно посчитать, со сколькими пунктами он связан дорогой. Считать можно по строкам или столбцам. Для определенности будем считать по строкам.

Чтобы посчитать степень для пункта А, посмотрим, сколько звездочек стоит в соответствующей строке. Их две – на пересечении строки А и столбцов В и Д. Значит, степень вершины А равна 2.

Аналогично считаем степени других вершин.

Задачи ЕГЭ (Тип 1)

Перейдем к заданиям из ЕГЭ. Примеры я беру из двух источников – сайта Решу ЕГЭ и сайта Константина Полякова. По моим наблюдениям, задания из первого источника не всегда близки к тем, что предлагают на экзамене (легкие задачи или устаревшие формулировки), но они подходят для знакомства с темой. На сайте К. Полякова задачи более актуальные, хотя бывают слишком сложного, не егэшного, уровня.

Задание 1 (Решу ЕГЭ, № 9354)

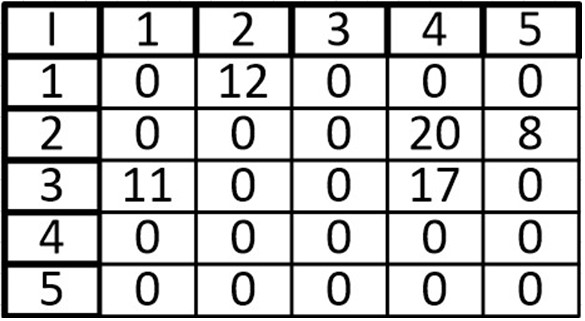
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.

Решение:

Итак, нужно определить номер пунктов В и Е в таблице и посмотреть, какое число стоит в ячейке на пересечении соответствующих строки и столбца.

Первым делом определяем степени вершин пунктов из условия.

Вершина В – степень 5.

Вершина Е – степень 4.

Дальше смотрим, есть ли еще вершины с такими степенями.

Вершины А, Б, Д, К – степень 2; вершина Г – степень 3. Получается, у нас есть только по одной вершине степени 5 и 4, и это В и Е.

Найдем пункты со степенями 4 и 5 в таблице.

Будем считать степени всех пунктов по порядку:

П1 – степень 2, П2 – степень 3, П3 – степень 2, П4 – степень 4 (значит, это Е), П5 – степень 2, П6 – степень 5 (это В).

Ищем число на пересечении столбца П4 и строки П6 (или наоборот, так как граф неориентированный, следовательно, таблица симметрична): 20. Это и будет ответом.

Задание 2 (Решу ЕГЭ, № 15619)

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о дорогах между населенными пунктами (звездочка означает, что дорога между соответствующими городами есть).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите номера населенных пунктов A и G в таблице. В ответе запишите числа в порядке возрастания без разделителей.

Решение:

Первое наше действие – определить степени вершин из вопроса.

Вершина A – степень 2.

Вершина G – степень 2.

Дальше смотрим, если ли еще вершины степени 2?

Да, есть. Это вершины С и Е.

А чем вершины A и G отличаются от вершин C и E?

Из графа видим, что вершины C и E связаны ребром с вершиной D (степени 3), а A и G связаны между собой и с вершиной В. Стоит отметить, что связь с вершиной В не дает нам никакой полезной информации, так как эта вершина связана ребрами со всеми остальными.

Получается, что, найдя в таблице пункт степени 3 (соответствующий вершине D), мы найдем три пункта, с которыми он связан. Два из них будут иметь степень 2 – C и Е, и один – степень 5 (вершина В). После этого мы будем знать, какие пункты соответствуют вершинам B, C, D и E, и методом исключения найдем A и G.

Сделаем это!

1. Пункт 2 имеет степень 3, значит, это D.
2. Пункт 2 связан с п.1 и п.6 степени 2 – значит, мы нашли С и Е.
3. Пункт 4 имеет степень 5 – это В.
4. На данном этапе имеем: п.1 и п.6 – это С и Е, п.2 – это D, п.4 – это В. Остаются пункты 3 и 5.
5. Читаем вопрос: «в ответе запишите числа в порядке возрастания без разделителей». Значит, ответ 35.

Примечание.

Почему в этой задаче просят найти номера двух пунктов, а не только А, к примеру?

Давайте посмотрим на граф (рис. 4).

В данной задаче граф симметричный (я провела фиолетовым ось симметрии). Это значит, что при поиске соответствий между графом и таблицей мы можем однозначно определить вершины, лежащие на оси симметрии (B и D, если нет дополнительных осей симметрии), и не можем однозначно определить симметричные вершины.

Поэтому в вопросе предлагают найти номера пунктов, соответствующих симметричным вершинам, и записать оба числа.

Это были простые задачи из ЕГЭ 2016 и 2018 года. Рассмотрим еще одну посложнее.

Задание 3 (сайт К. Полякова, № 4841)

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги ЗЕ равна 15 км. Определите длину дороги БГ. В ответе запишите целое число – длину дороги в километрах.

Решение:

По графу видно, что он симметричный, ось симметрии проходит по ребру ЗД. Получается, мы не можем отличить однозначно Е от Ж, А от Б, В от Г, а дорогу БГ, длину которой нужно найти, от дороги АВ. Но составители дают нам дополнительные данные – длину дороги ЕЗ (15 км).

Смотрим в таблицу. Дорог, равных 15, у нас четыре:

1. между п1 и п2 (п1 – степень 5, п2 – степень 2);
2. между п1 и п7 (п1 – степень 5, п7 – степень 3);
3. между п3 и п4 (п3 – степень 2, п4 – степень 3);
4. между п4 и п8 (п4 – степень 3, п8 – степень 3).

Какая из них ЕЗ? Смотрим на граф. Вершина Е имеет степень 3, вершина З – степень 3. У нас есть только одна дорога, соединяющая пункты со степенями 3 – дорога между п4 и п8.

Смотрим в таблицу. П4 связан с п1 (степень 5, это Д), п3 (степень 2) и п8 (степень 3). Значит, п4 – это Е, так как З связан с Д и с двумя пунктами степени 3.

Если п4 – это Е, то связанный с ним п3 со степенью 2 – это А. В свою очередь, п3 связан с п2 со степенью 2, значит, п2 – это В.

У нас осталось только два пункта со степенью 2 – п5 и п6. Значит, это Б и Г. Дорога из п6 в п5 (длина ребра БГ) равна 20. Это и будет ответом.

Примечание. Подобное решение может показаться запутанным, однако после некоторой тренировки с подобными задачами вполне можно справляться за три минуты, отведенные на них в спецификации. Ниже я дам список задач для самостоятельного решения. Рекомендую прорешать их все – я привожу примеры задач с разными формулировками, что позволяет посмотреть на одно и то же задание под разными углами.

Домашнее задание:

Сайт К. Полякова: №№ 5360, 5292, 4653, 4145, 3640, 3635, 3200, 2824, 88

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. 

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.  

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

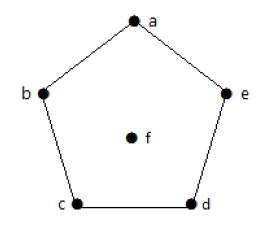
Для практического примера возьмем самый обыкновенный неориентированный граф:

А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

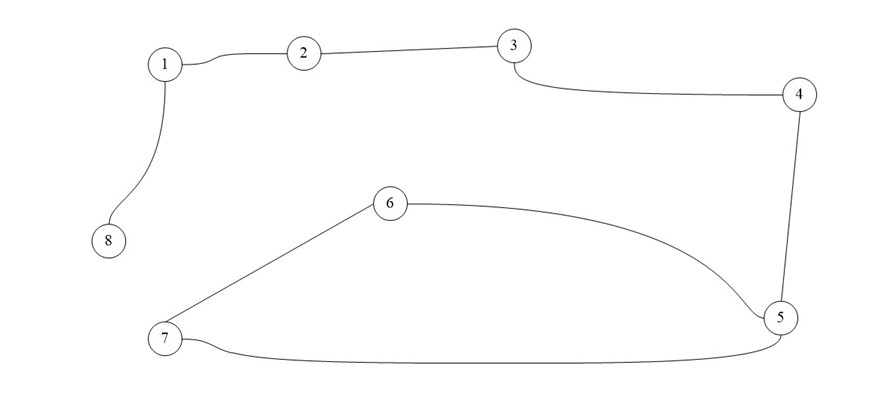
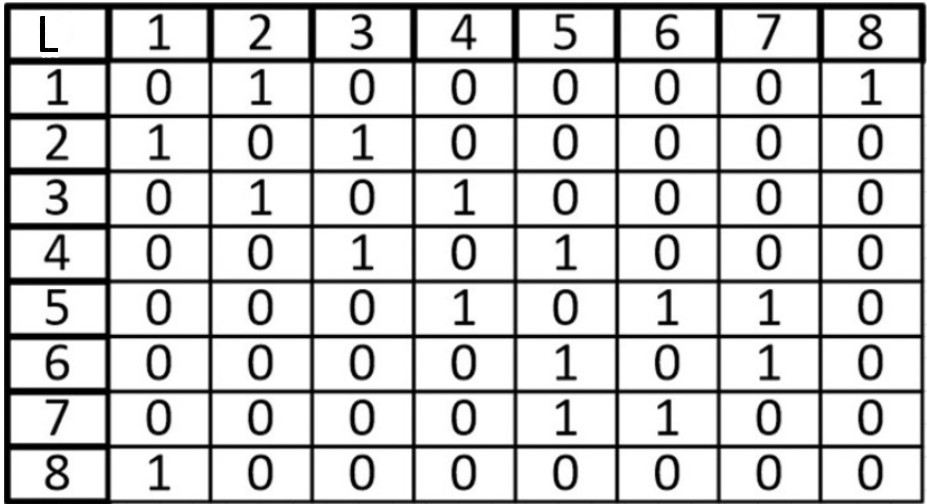
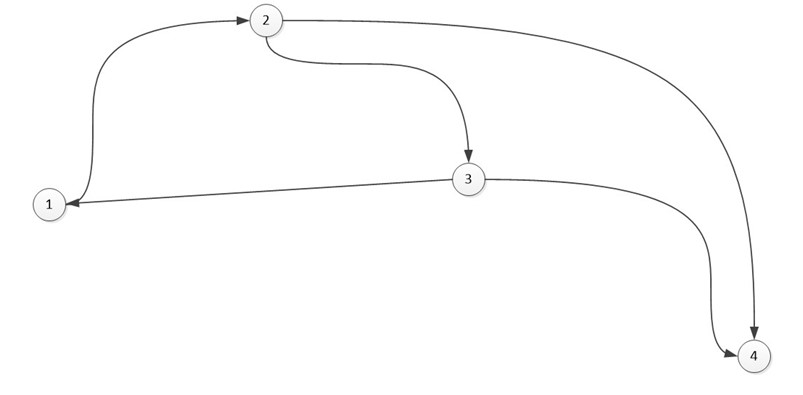
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном – единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

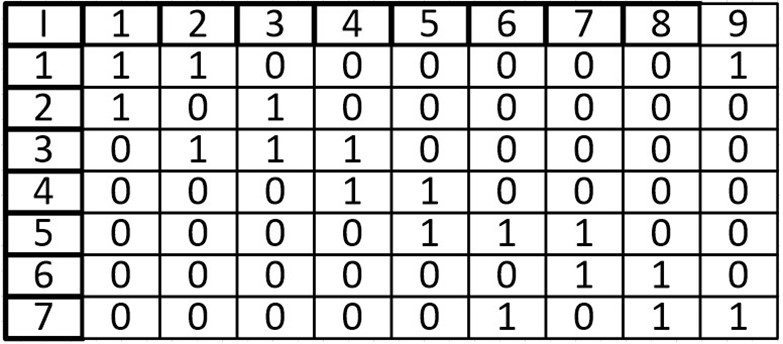
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

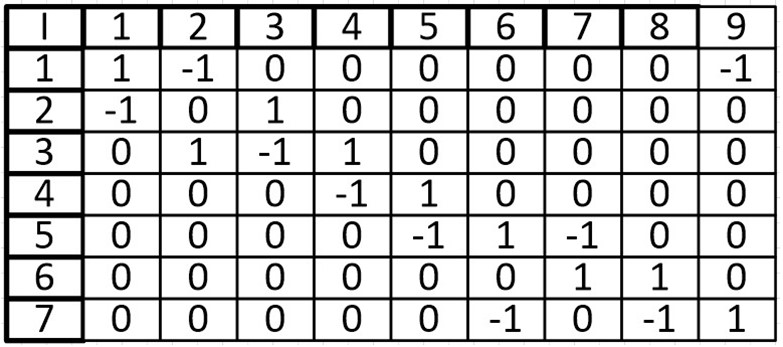
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

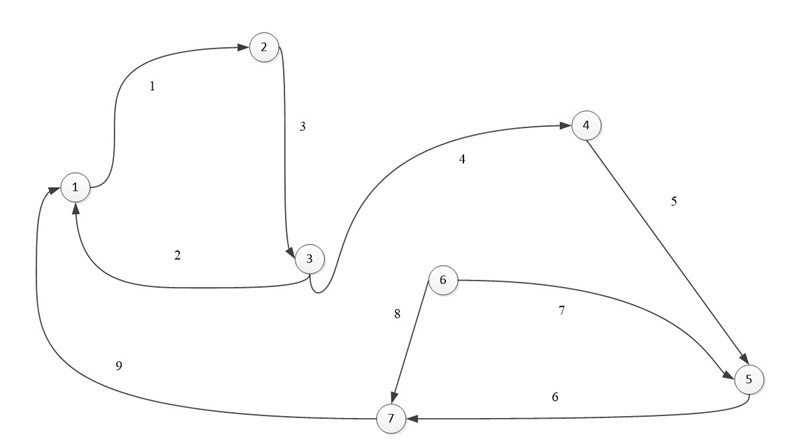
Ориентированный граф:

В виде матрицы:

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

Список смежности (инцидентности)

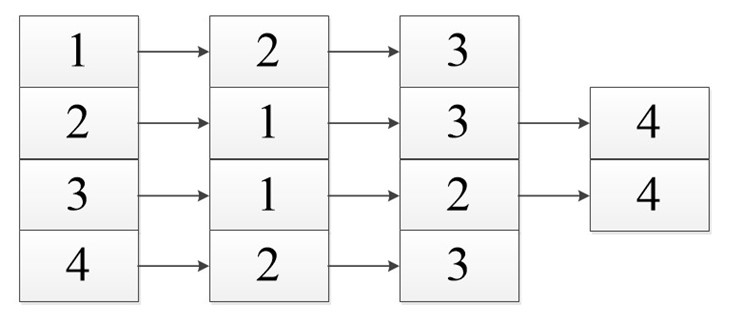
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

В виде списка:

Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф – это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

На каком языке программирования проводить операции с графами

Проголосовали 47 пользователей.

Воздержались 8 пользователей.