Как найти сторону через периметр основания

Содержание

• – Как найти сторону треугольника по его периметру?
• – Как найти стороны равнобедренного треугольника по его периметру?
• – Как найти сторону треугольника зная периметр и сторону?
• – Как найти стороны с помощью периметра?
• – Как найти третью сторону треугольника по двум сторонам и периметру?
• – Как найти длины сторон прямоугольника если известен периметр?
• – Как найти периметр равностороннего треугольника по его высоте?
• – Что такое периметр равнобедренного треугольника?
• – Как найти сторону равнобедренного треугольника если известно основание?
• – Как найти стороны прямоугольника если известна его площадь?
• – Как найти третью сторону треугольника 4 класс?
• – Как найти площадь треугольника формулы?
• – Как найти стороны прямоугольника?
• – Что нужно сделать чтобы найти ширину прямоугольника?
• – Что нужно сделать чтобы найти длину прямоугольника?

Периметр (P) представляет собой сумму всех сторон треугольника: P=a+b+c.

Как найти сторону треугольника по его периметру?

Чтобы найти длину стороны равностороннего треугольника, если известен его периметр, надо: 1) периметр разделить на 3 , 2) периметр умножить на 3 , 3) вычесть из периметра длину двух сторон.

Как найти стороны равнобедренного треугольника по его периметру?

P=2a+b, где b-это основание треугольника, a-значение боковой стороны. Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон.

Как найти сторону треугольника зная периметр и сторону?

Тогда длина стороны равна одной четвертой периметра: a = p/4. Легко разрешима эта задача и для равностороннего треугольника. У него три одинаковых по длине стороны, поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.

Как найти стороны с помощью периметра?

Для квадрата или ромба задача найти стороны из периметра решается очень просто. Известно, что у этих двух фигур по 4 стороны и все они равны между собой, поэтому периметр p квадрата и ромба равен 4a, где a – сторона квадрата или ромба. Тогда длина стороны равна одной четвертой периметра: a = p/4.

Как найти третью сторону треугольника по двум сторонам и периметру?

Теорема косинусов в произвольном треугольнике гласит, что можно найти сторону в треугольнике, зная другие две стороны и угол между ними. Для того чтобы вычислить третью сторону треугольника нужно извлечь квадратный корень из разности от квадратов известных сторон их удвоенного произведения на косинус угла между ними.

Как найти длины сторон прямоугольника если известен периметр?

Периметр прямоугольника равняется удвоенной сумме двух смежных сторон a и b: Пер = 2 * (a + b). Следовательно, зная длину одной из сторон и периметр, находите длину другой стороны: b = Пер / 2 – a. В квадрате все стороны равны между собой.

Как найти периметр равностороннего треугольника по его высоте?

P = 2 * (√ a2 + h2) + 2 * a, где a — боковая сторона, h — высота.

Что такое периметр равнобедренного треугольника?

Формула вычисления периметра

Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра: P=2a+b, где b – это основание треугольника, a – значение боковой стороны.

Как найти сторону равнобедренного треугольника если известно основание?

Стороны равнобедренного треугольника

Отсюда, боковая сторона будет равна корню из суммы половины основания в квадрате и высоты, также возведенной в квадрат: а = √(b/2)2+h2, где а — боковая сторона, b/2 — половина основания, h — высота.

Как найти стороны прямоугольника если известна его площадь?

S=b* (P – 2*b), где b – длина стороны, P – периметр.

Как найти третью сторону треугольника 4 класс?

Вычисляется оно по следующей формуле: CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).

Как найти площадь треугольника формулы?

Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности. Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом: S = r * p, где p — полупериметр.

Как найти стороны прямоугольника?

сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.

Что нужно сделать чтобы найти ширину прямоугольника?

– ширина прямоугольника.

1. Этот метод применим только в том случае, когда даны периметр и длина прямоугольника.
2. Иногда формула записывается так: P = 2 ( w + h ) {displaystyle P=2(w+h)} , где h {displaystyle h} – высота прямоугольника, которая совпадает с длиной. [4] X Источник информации Переменные l {displaystyle l} и

Что нужно сделать чтобы найти длину прямоугольника?

Ответ или решение1

Периметр прямоугольника равен сумме всех его четырех сторон. С условия задачи известна ширина прямоугольника и его периметр. Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.

Интересные материалы:

Почему на Востоке России много действующих вулканов?
Почему Наполеон пошел войной на Россию?
Почему Россия начала войну с Австро Венгрией?
Почему Россия начала войну с Францией?
Почему Россия воевала с Францией в конце 18 века?
Почему у российских банков нет IBAN?
Почему в России Борису Пастернаку не дали Нобелевскую премию?
Почему в России любят суши?
Почему в России учатся по субботам?
Почему Волга важна для России?

Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.

Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.

Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.

Длина основания через среднюю линию и известное основание

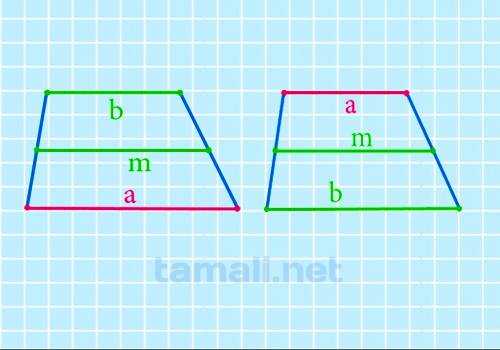
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:

a = 2m – b

Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.

Нижнее основание через верхнее основание, высоту и углы при нижнем основании

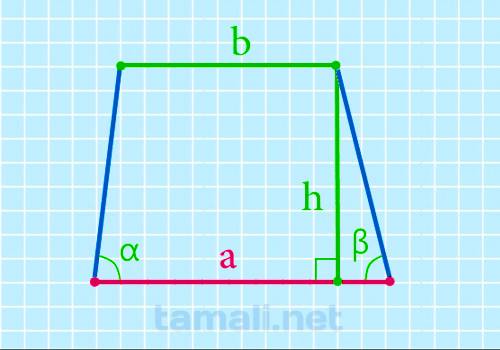
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:

a = b + h*(ctga + ctgb)

Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1

Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24

Верхнее основание через нижнее основание, высоту и углы при нижнем основании

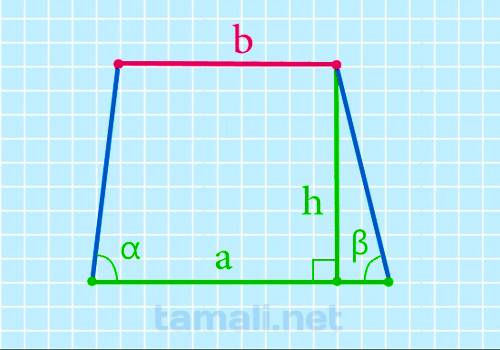
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:

b = a – h*(ctg α + ctg β)

Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31

Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.

• Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
• Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35

Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании

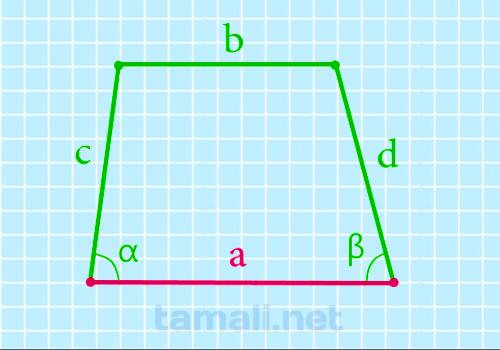
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них

a = b + c * cos α + d * cos β

Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82

Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.

• трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
  = (144 – 64)/4 = 20
• В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
  4*2*3/2 = 7 + 43

Верхнее основание через боковые стороны, нижнее основание и углы при нем

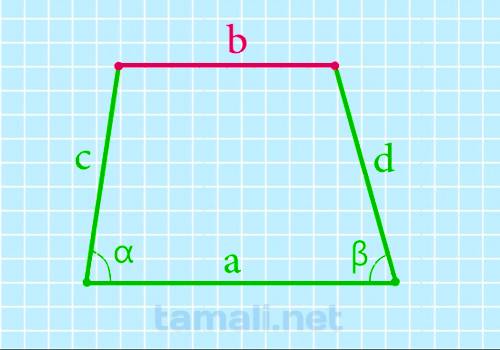
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них

b = a – c * cos α – d * cos β

Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.

• В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
  11*11)/12= (169 – 121)/12 = 4
• Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
  CD = 25 – 10*2*1/2 = 15

Боковая сторона через высоту и угол при нижнем основании

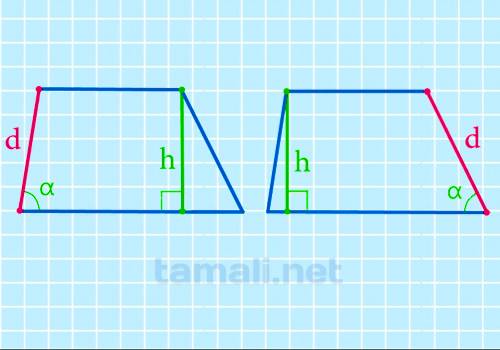
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней

d = h / sin α

Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243

Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)

• В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
  22*2/2 = 112
• Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
  градусам. Найти MP: MP = (32 – 19)*3 = 133
• В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
  AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269

Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.

Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.

• В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
  13)/3/2 = 103
• В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
  90
• В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
  (36 – 17)^2) = 841 – 361= 480 = 430

Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.

• В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
  100 – 96 = 4
• Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
  AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2
• В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
  Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2
• Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
  60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28

Виды трапеций

Существуют следующие виды трапеций:

• Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
  Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
  равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
  разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
  фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
• Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
  и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
  другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
  образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
  вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
  треугольник.
• Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
  являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
  остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
  градусов.

Свойства трапеции

1. Средняя линия параллельна основаниям и равна их полусумме.
2. Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
   отрезок с длиной боковой стороны.
3. Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
   Коэффициент
   подобия – k = AD/BC.
   Отношение площадей треугольников — k^2.
4. Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
   площадь.
5. В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
6. Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
   боковых сторон лежат на одной прямой.
7. Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
   линии.

Содержание

• – Как найти стороны по периметру?
• – Как найти сторону равностороннего треугольника зная его периметр?
• – Как найти стороны равнобедренного треугольника по его периметру?
• – Как найти стороны прямоугольника по его периметру?
• – Что такое периметр равнобедренного треугольника?
• – Как найти основание равнобедренного треугольника?
• – Как найти стороны треугольника зная одну сторону и периметр?
• – Как найти стороны прямоугольника по периметру и диагонали?
• – Как найти сторону квадрата по его периметру?

Тогда длина стороны равна одной четвертой периметра: a = p/4. Легко разрешима эта задача и для равностороннего треугольника. У него три одинаковых по длине стороны, поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.

Как найти стороны по периметру?

Как найти сторону прямоугольника если известен периметр и 1 сторона из периметра отнять два раза известную сторону,так как противолежащие стороны равны и останется сумма других двух сторон, а так как они равны то делим сумму пополам и получаем неизвестную сторону.

Как найти сторону равностороннего треугольника зная его периметр?

Чтобы найти длину стороны равностороннего треугольника, если известен его периметр, надо: 1) периметр разделить на 3 , 2) периметр умножить на 3 , 3) вычесть из периметра длину двух сторон.

Как найти стороны равнобедренного треугольника по его периметру?

Периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны: P = a + 2b.

Как найти стороны прямоугольника по его периметру?

Как найти сторону прямоугольника ,зная периметр и другую его сторону Р=2а+2b.

Что такое периметр равнобедренного треугольника?

где a,b,c – стороны равнобедренного треугольника. То есть периметр треугольника равен сумме всех его сторон.

Как найти основание равнобедренного треугольника?

Треугольник называется равнобедренным, если у него есть две равные стороны. Посмотри как это выглядит: Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон. Две равные стороны называются боковыми сторонами, а третья сторона – основанием.

Как найти стороны треугольника зная одну сторону и периметр?

Тогда длина стороны равна одной четвертой периметра: a = p/4. Легко разрешима эта задача и для равностороннего треугольника. У него три одинаковых по длине стороны, поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.

Как найти стороны прямоугольника по периметру и диагонали?

Как найти стороны прямоугольника если известна диагональ и периметр

1. Периметр нашего прямоугольника делим на 2. …
2. Выражаем одну из сторон прямоугольника.
3. Составляем уравнение с двумя неизвестными по теореме Пифагора, где нашу диагональ возводим в квадрат.

Как найти сторону квадрата по его периметру?

Если известен периметр, то нужно просто разделить периметр на 4, вот тебе и сторона квадрата.

Интересные материалы:

Как принимать витамины Алфавит для мужчин?
Как приобрести слуховой аппарат?
Как приподнять настроение девушке?
Как приподнять веко с помощью макияжа?
Как пришить резинку на швейной машине?
Как прицепить накладной хвост?
Как приучить волосы на другой пробор?
Как привязать фитнес часы к айфону?
Как признаться в любви девочке?
Как признаться в любви своей девушке?

Стороны треугольника

Свойства

Зная стороны треугольника, можно найти все остальные его параметры по выведенным для треугольника формулам, просто подставив их значения. Периметр треугольник будет представлять собой сумму всех его сторон, а площадь выводится по формуле Герона, как квадратный корень из произведения полупериметра на его разность с каждой стороной по очереди, и деленному на два. P=a+b+c S=√(p(p-a)(p-b)(p-c)/2)

Все углы в треугольнике, зная стороны, можно найти через теорему косинусов. (рис.75) cos⁡α=(b^2+c^2-a^2)/2bc

В произвольном треугольнике также есть три медианы m (делящие противоположную сторону пополам), три биссектрисы l (делящие угол пополам) и три высоты h (перпендикуляры из угла к стороне или ее проекции). Все их можно вычислить, имея в распоряжении значения трех сторон. Формула медианы, которая опущена на сторону c.(рис.75.1) m_c=√(2a^2+2b^2-c^2 )/2

Найти медиану, опущенную на сторону a или b, можно заменив необходимые стороны в формуле так, чтобы сторона, поделенная медианой пополам, была со знаком «–». m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2

Формула биссектрисы, которая выходит из угла γ и опущена на сторону с. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b)

Чтобы найти биссектрисы, которые выходят из двух других углов, нужно преобразовать формулу аналогично формуле медианы, где противоположная сторона со знаком «–». l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)

Формула высоты, которая опущена на сторону a, b или c видоизменяется таким образом, чтобы в знаменателе была нужная сторона.(рис.75.3) h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c

Также в любом треугольнике можно провести среднюю линию, которая также как медиана обозначается буквой m, поэтому для их разделения, будем использовать заглавную M для средней линии. Средняя линия параллельна той стороне, которая выбрана основанием треугольника, и равна ее половине. Среди свойств средней линии можно отметить, что боковые стороны она делит на две равные части, поэтому если начертить все три средние линии в треугольнике, то получится еще один треугольник, подобный первому, в два раза меньше. (рис. 75.7) M_a=a/2 M_b=b/2 M_c=c/2

В каждый треугольник можно вписать окружность и описать ее вокруг него. Центр вписанной в треугольник окружности будет находиться на пересечении его биссектрис, а радиус будет опущен под прямым углом к любой стороне и его формула выводится также по Герону. (рис.75.5) r=√(((p-a)(p-b)(p-c))/p)

Центр описанной вокруг произвольного треугольника окружности находится на пересечении его медиатрисс (срединных перпендикуляров, радиус опущен в любую вершину или угол, и вычисляется по следующей формуле. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Формулы периметра треугольника

Как найти периметр любого треугольника? Существует
множество способов сделать это, но мы расскажем про
основные. В этой статье вы узнаете, как найти периметр
любого треугольника через известные величины, по формулам.

Ⅰ. Через площадь и радиус вписанной окружности

Известно: площадь и радиус вписанной окружности треугольника.

Чтобы найти периметр любого треугольника,
нужно две площади треугольника разделить
на радиус вписанной окружности.

Как видим, для этой формулы нужно знать всего
лишь радиус вписанной окружности и площадь.

Ⅱ. Через три стороны

Известно: три стороны треугольника.

Чтобы найти периметр любого треугольника,
нужно сложить все стороны треугольника.
Результатом и будет периметр.

Это самая простая формула.

Ⅲ. Через Теорему Косинусов

Известно: две стороны и угол между ними.

Чтобы найти периметр любого треугольника,
нужно для начала найти третью сторону треугольника,
затем косинус угла, если косинус неизвестен.

Это формулу удобней применить,
если вам известны две стороны
и косинус между ними.

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

http://colibrus.ru/formuly-perimetra-treugolnika/

[/spoiler]