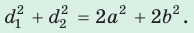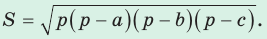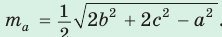Загрузить PDF
Загрузить PDF
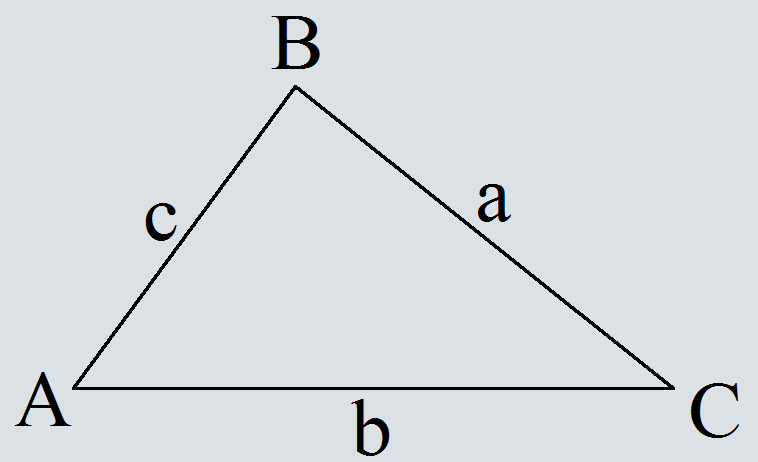
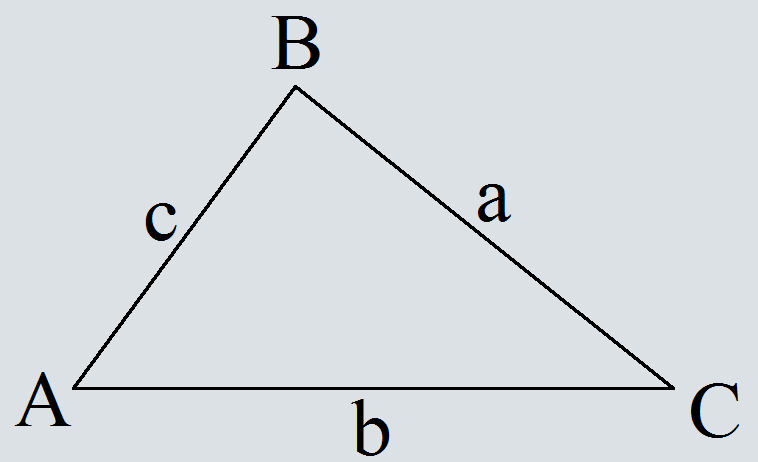
Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике 
-
1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
-
2
Запишите формулу теоремы косинусов. Формула:
, где
— неизвестная сторона,
— косинус угла, противоположного неизвестной стороне,
и
— две известные стороны.[2]
-
3
-
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку
. Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.[4]
Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.- Например, косинус 89° ≈ 0,01745. Итак:
.
- Например, косинус 89° ≈ 0,01745. Итак:
-
5
Перемножьте числа. Умножьте
на косинус известного угла.
-
6
Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
-
7
Вычтите два числа. Вы найдете
.
-
8
Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.[5]
Реклама
-
1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
-
2
Запишите формулу теоремы косинусов. Формула:
, где
— косинус неизвестного угла,
— известная сторона, противолежащая неизвестному углу,
и
— две другие известные стороны. [7]
-
3
-
4
Перемножьте числа. Умножьте
на косинус неизвестного угла.
- Например,
.
- Например,
-
5
Возведите
в квадрат. То есть умножьте число само себя.
- Например,
- Например,
-
6
Сложите квадраты
и
. Но сначала возведите соответствующие числа в квадрат.
-
7
Изолируйте косинус неизвестного угла. Для этого вычтите сумму
и
из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
-
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.[9]
На калькуляторе функция арккосинуса обозначается.
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама
-
1
Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
-
2
Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
-
3
Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.
Реклама
Советы
- Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.
Реклама
Об этой статье
Эту страницу просматривали 5394 раза.
Была ли эта статья полезной?
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
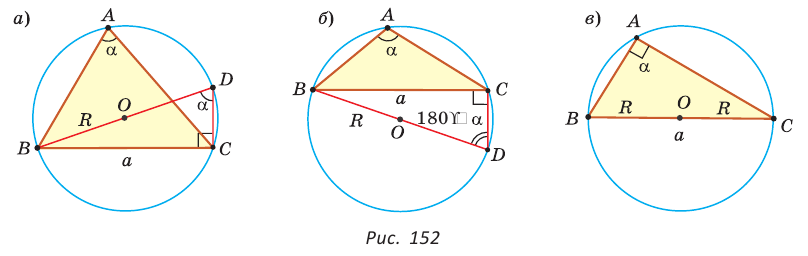
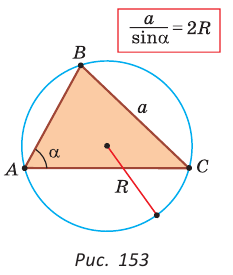
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
Пусть дан треугольник АВС, ВС = 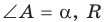
1) Угол 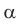
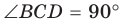
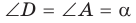
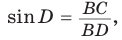
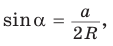
2) Угол 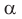
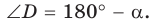
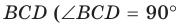
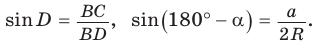
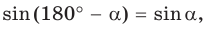
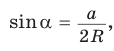
3) Для 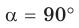
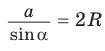
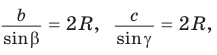
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 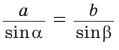
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 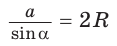
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
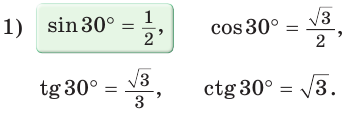
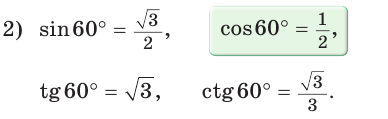
Пример:
В остроугольном треугольнике известны стороны 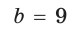
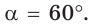
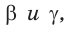
Решение:
По теореме синусов 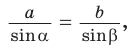
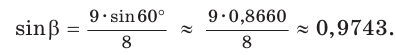
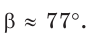
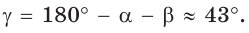
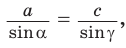
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 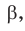
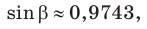
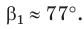
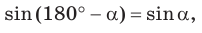
Пример:
Доказать справедливость формулы площади треугольника 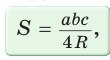
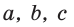
Доказательство:
Воспользуемся известной формулой площади треугольника: 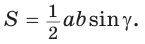
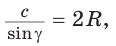
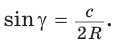
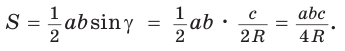
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
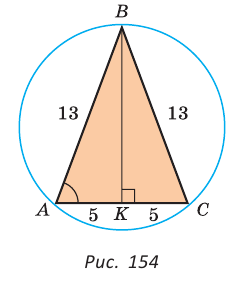
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 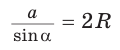
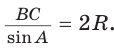
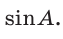
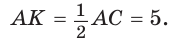
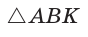
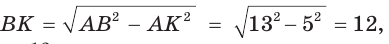
Тогда
Способ 2. Используем формулу 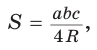
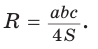
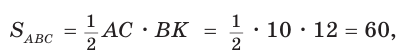
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 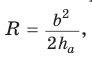
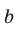
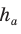
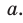
Заменив 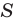
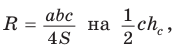
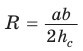

Теорема косинусов
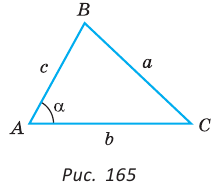
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 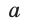
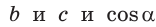
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
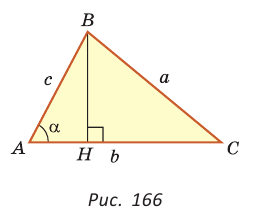
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 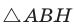
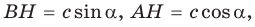
Из 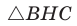
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 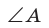
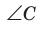
Для сторон 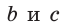
Замечание. Если 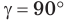
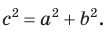
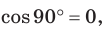
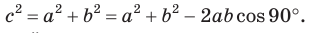
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
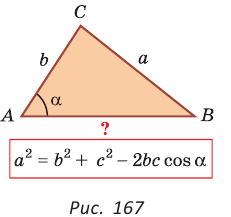
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 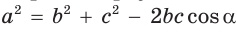
Для углов 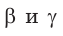
Пример:
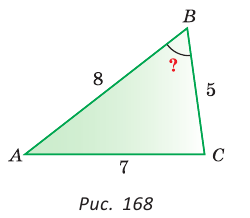
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 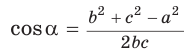
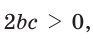
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 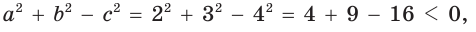
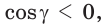
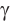
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
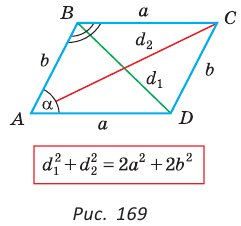
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 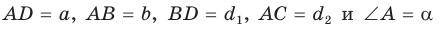
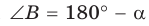
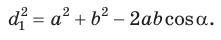
Из 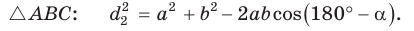
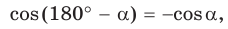
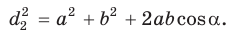
Сложив почленно равенство (1) и равенство (2), получим 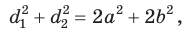
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
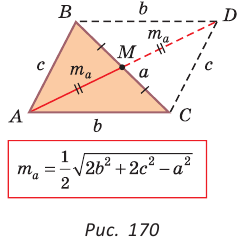
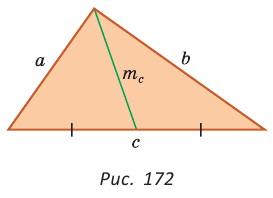
Медиану 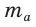
Доказательство:
Рассмотрим 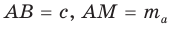
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 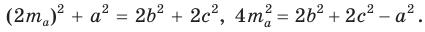
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 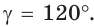
Решение:
а) По теореме косинусов
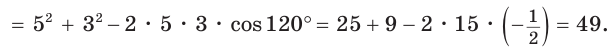
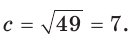
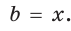
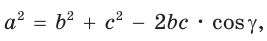
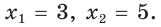
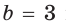
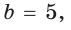
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 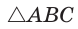
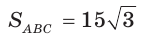
Поскольку 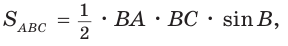
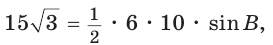
Так как 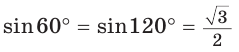
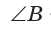

Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 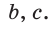
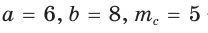
По формуле медианы 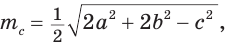
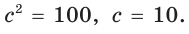
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 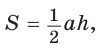
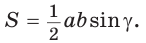
Теорема (формула Герона).
Площадь треугольника со сторонами 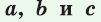
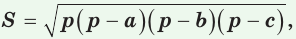
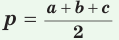
Доказательство:
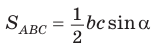
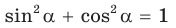
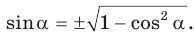
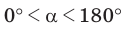
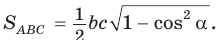
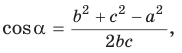
Тогда
Так как
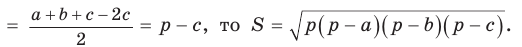
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
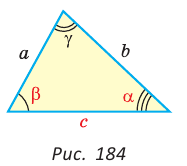
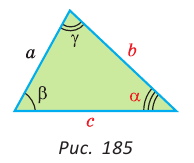
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 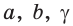
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 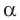
4) Угол
Замечание. Нахождение угла 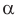
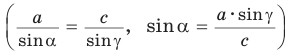
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 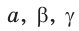
Найти:
Решение:
1) Угол
2) По теореме синусов 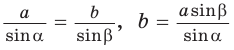
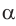
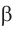
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 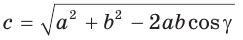
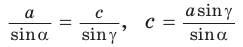
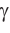
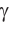
Пример №3 (решение треугольника по трем сторонам).
Дано: 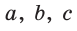
Найти: 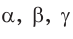
Решение:
1) По следствию из теоремы косинусов
2) Зная 
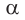
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 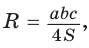
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 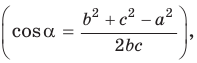
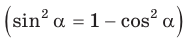
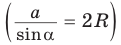
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
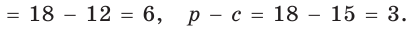
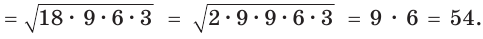
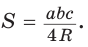
Ответ:
Способ 2. Так как 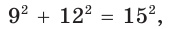
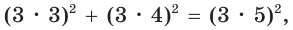
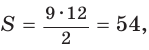
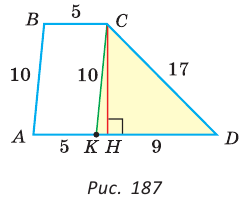
Пример №5
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 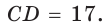
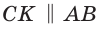
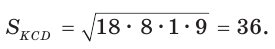
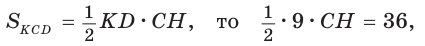
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
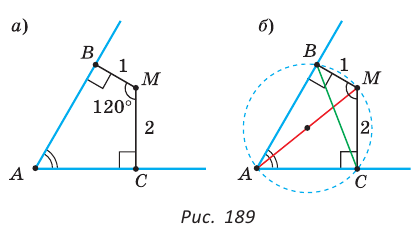
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 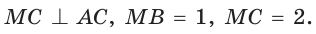
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 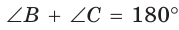
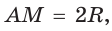
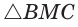
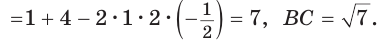
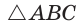
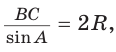
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
В прямоугольном треугольнике АВС известно: 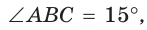
Решение:
Построим 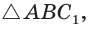
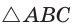
Поскольку 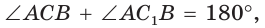
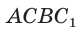
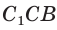
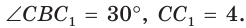
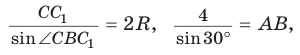
Ответ: 8.
Пример №7
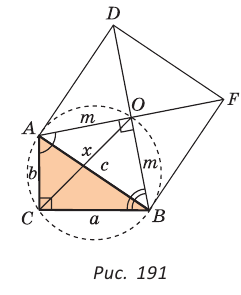
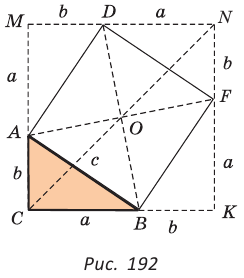
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 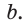
Решение:
Способ 1. Так как 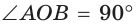
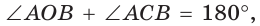
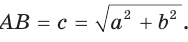
Пусть СО = х. По теореме косинусов из 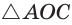
из 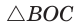
По свойству вписанного четырехугольника 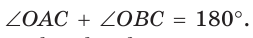
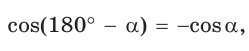
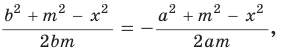
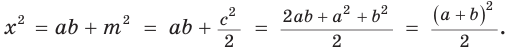
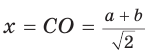
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 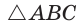
Ответ:
Пример №8
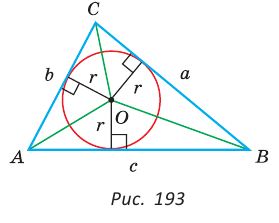
Точка О — центр окружности, вписанной в треугольник АВС, 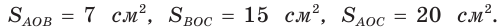
Решение:
Пусть 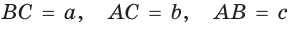
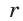
Тогда
Отсюда 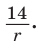
С другой стороны, 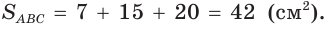
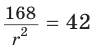
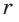
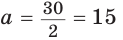
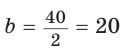
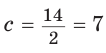
Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
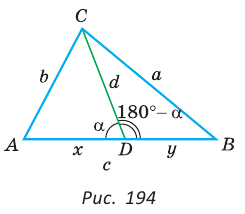
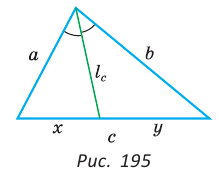
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 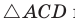
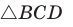
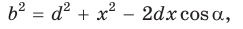
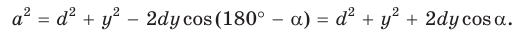
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
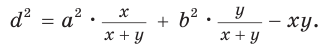
Следствие:
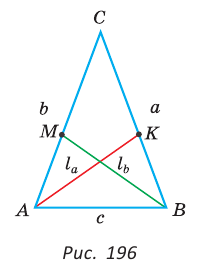
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 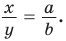
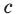
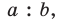
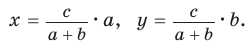
Пример №9
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 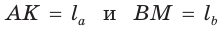
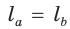
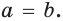
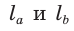
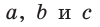
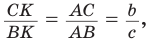
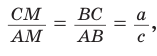
По формуле биссектрисы треугольника
Из условия 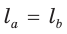
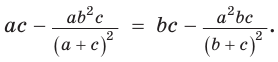
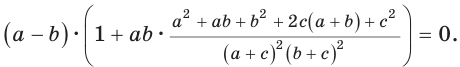
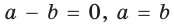
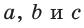
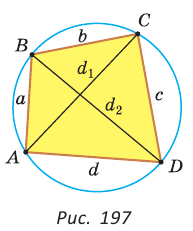
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.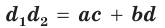
Доказательство:
Из 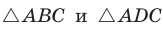
Так как 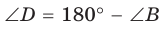
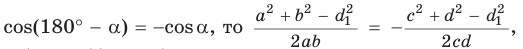
Аналогично из 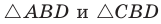
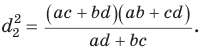
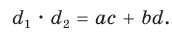
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
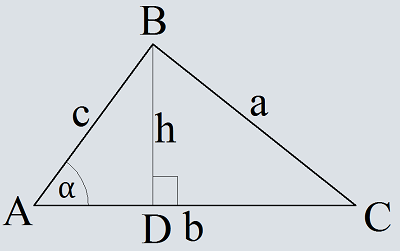
Треугольник. Расчет сторон прямоугольного треугольника через тригонометрические функции.
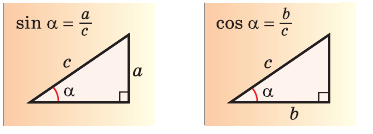
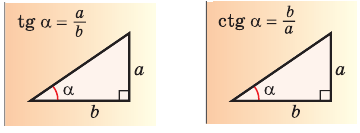
Проанализируем прямоугольный треугольник ABC в котором обозначим катеты как а, b и гипотенузу как с соответственно.
Вполне логично сделать вывод, будут верны следующие равенства:
Значит катет прямоугольного треугольника допускается представить как произведение гипотенузы и синуса угла, противолежащего этому катету, либо и косинуса угла, прилежащего к нему.
На основе этих соотношений так же можно определить гипотенузу прямоугольного треугольника:
Иначе говоря, гипотенуза будет частным от деления катета либо на синус противолежащего к нему угла, либо на косинус прилежащего к катету угла.
Значит, катет прямоугольного треугольника допускается представить как произведением другого катета на тангенс угла, противолежащего первому катету, либо на котангенс угла, прилежащего к первому катету.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
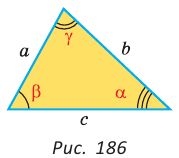
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
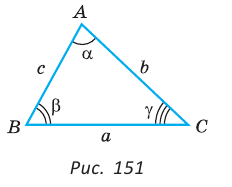
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2 bc · cos α
b 2 = a 2 + c 2 – 2 ac · cos β
c 2 = a 2 + b 2 – 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 – a 2
mb = 1 2 √ 2 a 2 +2 c 2 – b 2
mc = 1 2 √ 2 a 2 +2 b 2 – c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p – a ) b + c
lb = 2√ acp ( p – b ) a + c
lc = 2√ abp ( p – c ) a + b
где p = a + b + c 2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
http://ru.onlinemschool.com/math/formula/triangle/
[/spoiler]
Теорема косинусов
Определение теоремы косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
a2=b2+c2-2*b*c*cos(A)
b2=a2+c2-2*a*c*cos(B)
c2=a2+b2-2*a*b*cos(C)
Расчёт стороны по теореме косинусов
Введите сторону
Введите сторону
Введите угол
Формула расчёта стороны по теореме косинусов
Где a, b и c – стороны треугольника,
A – угол между сторонами b и c
Расчёт углов треугольника по теореме косинусов
Введите сторону a
a =
Введите сторону b
b =
Введите сторону c
c =
Формулы расчёта углов по теореме косинусов
Где a, b и c – стороны треугольника,
A, B и C – углы треугольника
Доказательство теоремы косинусов
Дано
Треугольник со сторонами a, b и c.
Доказать
a2=b2+c2-2*b*c*cos(α)
Доказательство
Из вершины B проведём высоту h
Сравним и упростим
Теорема доказана
В статье про прямоугольный треугольник посмотрели задачи связанные с синусами и косинусами из 1 части ОГЭ. Так что обязательно заглядывай.
Получается, что решить прямоугольный треугольник (найти все стороны и острые углы) можно довольно просто, зная всего лишь два элемента прямоугольного треугольника :две стороны (по теореме Пифагора) или сторону и острый угол (из определений синуса, косинуса, тангенса).
Но решить треугольник (найти все стороны и углы ) можно и произвольный, зная три элемента: три стороны, две стороны и угол, или два угла и сторону.
Для первых двух случаев в решении пользуются теоремой косинусов (вполне возможно эта тема вас поджидает уже на следующей неделе в школе, а может уже и была):
в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
- Если известны три стороны треугольника можно найти косинусы всех углов
- Если известны две стороны и угол между ними треугольника, то можно найти третью сторону.
В этом случае полезно пользоваться таблицей значений косинусов некоторых углов :
Рассмотрим решение задачи №16 из сборника Ященко (36 вариантов) на теорему косинусов :
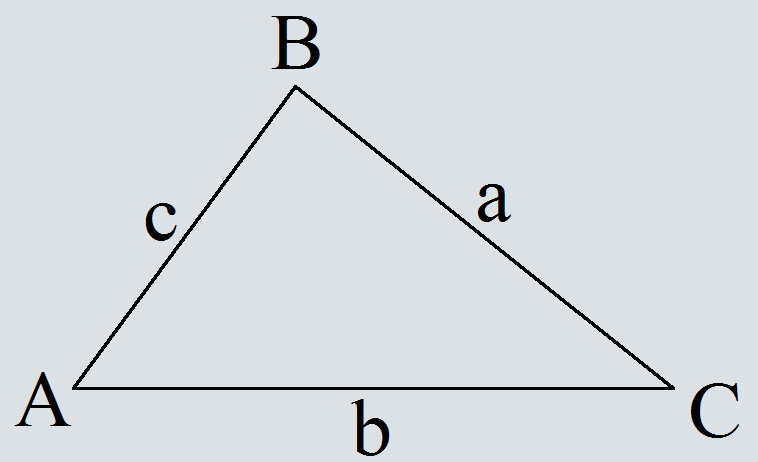
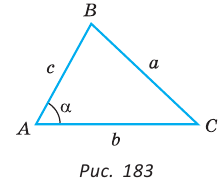
Изобразим треугольник АВС и найдем в нем противолежащую сторону для угла АВС.
Из рисунка видно, что противолежащая сторона – это сторона АС.
Для стороны АС записываем теорему косинусов:
Подставим значения всех сторон:
Переносим все “свободные” числа (меняя знак) в левую часть равенства и считаем:
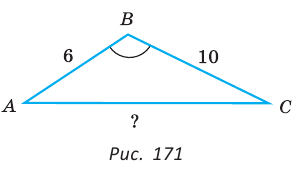
Находим косинус угла АВС, как неизвестный множитель:
Записываем ответ:
Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.
































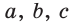
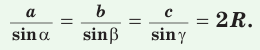
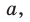
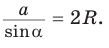
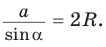
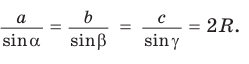
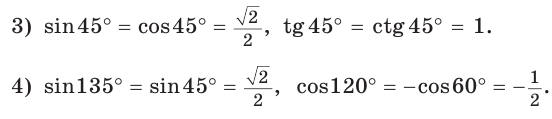
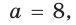
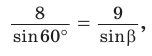
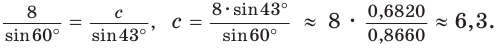
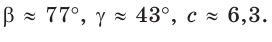


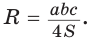
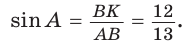
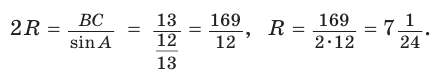
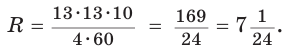
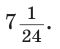
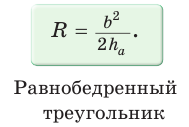
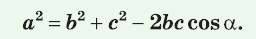
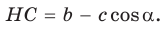
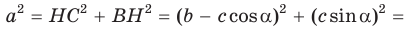
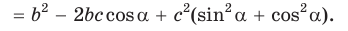
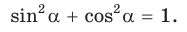
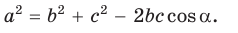
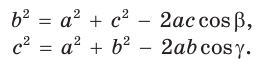
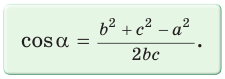
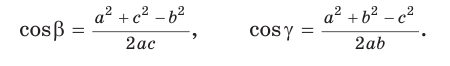

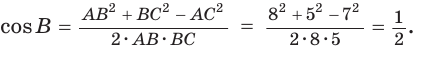
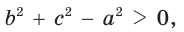 то
то 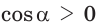 и угол
и угол 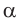 острый;
острый;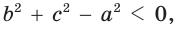 то
то 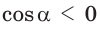 и угол
и угол 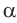 тупой;
тупой; то
то 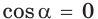 и угол
и угол 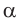 прямой.
прямой.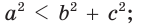
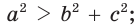
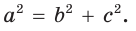
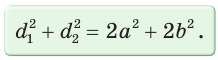
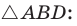
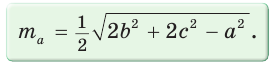
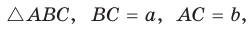
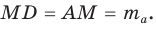
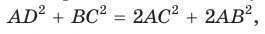
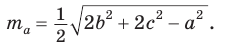
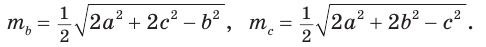
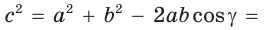
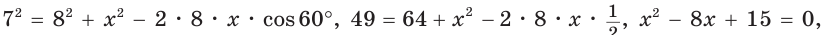
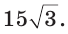
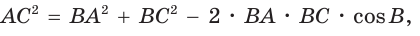
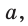
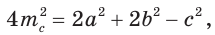
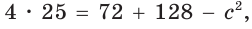
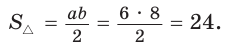
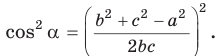
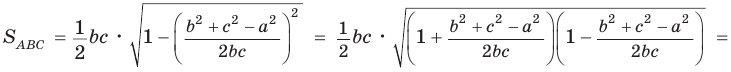
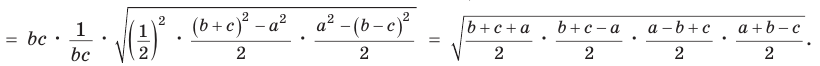
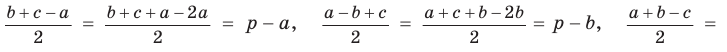
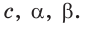
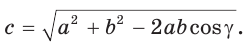
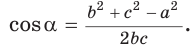
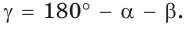
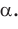
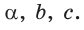
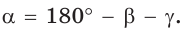
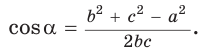
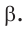
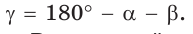
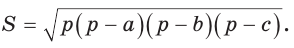
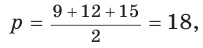
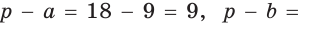
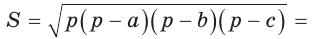
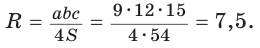
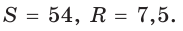
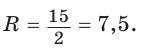
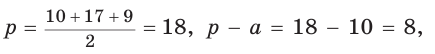
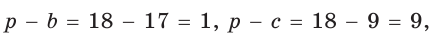
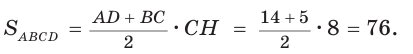
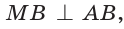
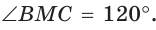
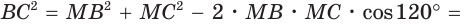
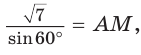
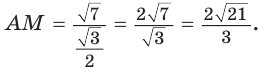
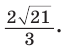
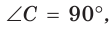
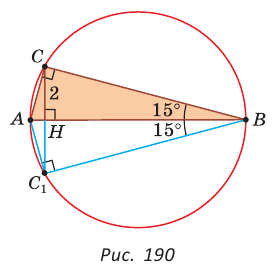
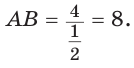
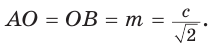
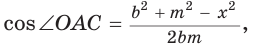
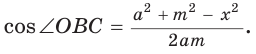
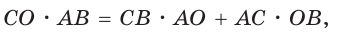
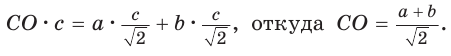
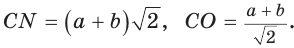
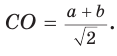
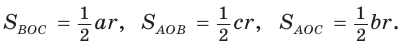
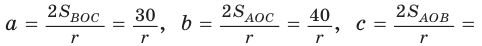
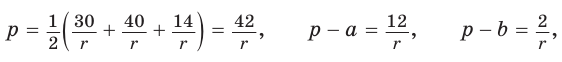
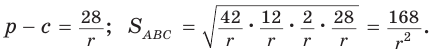
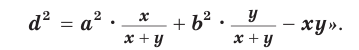
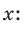
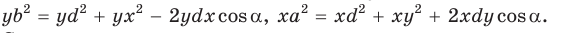
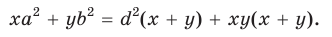
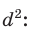
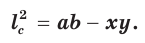
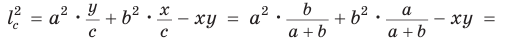
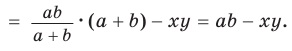
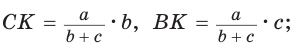
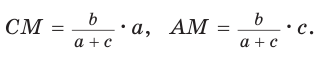
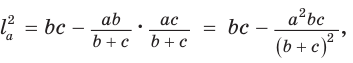
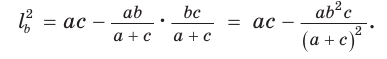
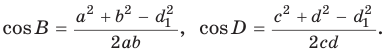
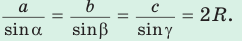
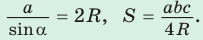
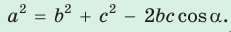
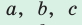 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 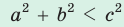 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 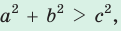 то треугольник остроугольный, если
то треугольник остроугольный, если 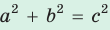 , то треугольник прямоугольный.
, то треугольник прямоугольный.