Как найти сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней куба называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).
Вам понадобится
- калькулятор
Инструкция
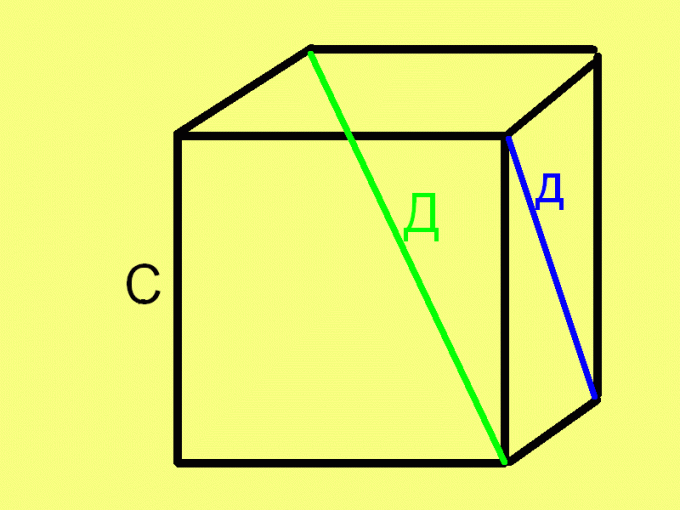
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П – площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ – функция извлечения кубического корня).
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Полезный совет
Для нахождения квадратных и кубических корней воспользуйтесь инженерным калькулятором. Чтобы извлечь корень третьей степени возведите число в степень ⅓.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также
Содержание
- – Как вычислить объем куба?
- – Как определить грань куба?
- – Как найти объем куба если известна длина ребра?
- – Как называется сторона куба?
- – Как найти площадь поверхности куба?
- – Как вычислить объем прямоугольника?
- – Как найти Объëм?
- – Как посчитать м3 помещения?
- – Что такое грань определение?
- – Какие свойства имеет куб?
- – Как узнать объем цилиндра формула?
Как вычислить объем куба?
Куб – это геометрическая фигура, которая представляет собой правильный многогранник, где каждая его грань является квадратом. Объем куба можно вычислить, зная только значение длины его ребра. Так как все его ребра между собой равны. Говоря проще объем куба приравнивается кубу длины его ребра.
Как определить грань куба?
Грань куба – это часть плоскости, ограниченная сторонами квадрата. – куб имеет шесть граней; – каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани; – грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.
Как найти объем куба если известна длина ребра?
Все довольно просто. Объем = длина*ширина*высота. Ребро куба – это и есть его сторона, а все стороны в кубе равны. Следовательно, V= 1*1*1 = 1 кубический см.
Как называется сторона куба?
Куб – это многогранник, поверхность которого состоит из шести квадратов. Грани куба – это стороны куба, которые представляют собой квадрат. Ребра куба – это стороны граней куба. Вершина куба– это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.
Как найти площадь поверхности куба?
Куб – это один из пяти типов правильных многогранников, являющийся правильным прямоугольным параллелепипедом, имеет шесть граней, каждая из которых является квадратом. Площадь поверхности куба равна сумме площадей всех его шести граней.
Как вычислить объем прямоугольника?
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Как найти Объëм?
Объем параллелепипеда равен произведению площади основания на высоту.
…
V = a * b * h.
| a | длина параллелепипеда |
|---|---|
| h | высота параллелепипеда |
| P (осн) | периметр основания |
| S (осн) | площадь основания |
| S (бок) | площадь боковой поверхности |
Как посчитать м3 помещения?
К = Д х Ш х В, где: К – кубатура помещения (объем, выраженный в кубических метрах), Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно. Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.
Что такое грань определение?
Грань — многозначный термин: Грань — плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Грань — часть цифр большого числа, выделенная из него каким-нибудь знаком. Грань числового множества — обобщение понятий максимума и минимума множества.
Какие свойства имеет куб?
Свойства куба:
- В кубе 6 граней и все они являются квадратами.
- Противоположные грани попарно параллельны.
- Все двугранные углы куба – прямые.
- Диагонали равны.
- Куб имеет 4 диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Диагональ куба в √ 3 раз больше его ребра
Как узнать объем цилиндра формула?
Формулы для вычисления объема цилиндра
$ V = pi r^2 h$ где: π – число пи (3.1415); h – высота цилиндра; r – радиус основания.
Интересные материалы:
Как заменить стандартный плеер на андроид?
Как запаривать пшеницу для бройлеров?
Как заправить узкий скотч в маленький диспенсер?
Как заправить зажигалку газом?
Как заправляется домкрат?
Как заправлять баллон со сливками?
Как запустить диспетчер печати через командную строку?
Как запустить Epson Status Monitor?
Как запустить каталитическую очистку духовки?
Как запустить квадрокоптер с пульта?
Содержание
- – Чему равна длина ребра куба?
- – Как вычислить длину стороны куба?
- – Как определить сумму длин всех рёбер куба?
- – Сколько ребер у куба?
- – Чему равна длина ребра куба если сумма всех рёбер составляет 720 см?
- – Как вычислить площадь ребра куба?
- – Как вычислить длину ребра?
- – Как найти объем куба зная его ребро?
- – Сколько сторон у куба?
- – Как найти сумму длин всех рёбер и площадь поверхности куба если его ребро равно 7 см?
- – Какая из формул выражает длину всех ребер куба?
- – Какая из формул выражает длину всех рёбер прямоугольного параллелепипеда?
- – Как в математике обозначается ребро куба?
- – Можно ли из всех ребер куба?
- – Чему равны диагонали куба с ребром а?
Чему равна длина ребра куба?
Р = 12 * а, где а – длина ребра куба. Отсюда находим, что: а = Р / 12.
Как вычислить длину стороны куба?
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба.
Как определить сумму длин всех рёбер куба?
Значит для нахождения суммарной длины всех ребер, надо узнать длину одного ребра и увеличить его в двенадцать раз. Умножайте длину одного ребра куба (A) на двенадцать, чтобы вычислить длину всех ребер куба (L): L=12∗A. Это самый простой из возможных способов определения суммарной длины ребер правильного гексаэдра.
Сколько ребер у куба?
| Куб | |
|---|---|
| Тип | правильный многогранник |
| Комбинаторика | |
| Элементы | 6 граней 12 рёбер 8 вершин Χ = 2 |
| Грани | квадраты |
Чему равна длина ребра куба если сумма всех рёбер составляет 720 см?
Ответ: Длина ребра куба – 70 см или 7 дм.
Как вычислить площадь ребра куба?
Формула вычисления площади куба
- Через длину ребра Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате. S = 6 ⋅ a2 …
- Через длину диагонали грани Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.
Как вычислить длину ребра?
Ребро куба
- V = a3 , где Y — объем куба, а — ребро куба. Если известен объем куба V, длину ребра (а) рассчитываем по формуле: …
- d = a√3 , где а — ребро куба, d — диагональ куба. Если известна диагональ куба, его ребро определяем как отношение диагонали к корню из 3 по формуле:
- a = d/√3 , Диагональ куба d. Ребро куба a.
Как найти объем куба зная его ребро?
Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т. к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
Сколько сторон у куба?
Правильно, у куба 6 граней. Стороны граней (квадратов) называют ребрами куба.
Как найти сумму длин всех рёбер и площадь поверхности куба если его ребро равно 7 см?
Сумма длин всех ребер
Куб имеет 12 ребер, поэтому, для того, чтобы узнать сумму длин всех его ребер, достаточно 12 умножить на длину одного ребра, по условию задачи это 7 см. получаем 12 * 7 = 84 см. Ответ: S = 294 см^2; 84 см – сумма длин всех ребер куба.
Какая из формул выражает длину всех ребер куба?
L= 12a – где а – сторона (ребро) куба.
Какая из формул выражает длину всех рёбер прямоугольного параллелепипеда?
4) 52 + 64 + 84 = 200 (см) – сумма длин всех ребер прямоугольного параллелепипеда. Таким образом, для нахождения суммы длин всех ребер прямоугольного параллелепипеда можно вывести формулу: Z = 4a + 4b + 4c (где Z – сумма длин ребер).
Как в математике обозначается ребро куба?
Рёбра Куб имеет 12 рёбер. Ребро обозначается двумя буквами вершин, расположенных на концах ребра. Например: АВ, DH.
Можно ли из всех ребер куба?
У фигуры из шести квадратных граней может быть только двенадцать ребер. Так как все грани – это одинаковые по размерам квадраты, то и длины всех ребер равны. … Если известна длина диагонали куба (D), то для нахождения одного ребра это значение надо разделить на квадратный корень из трех.
Чему равны диагонали куба с ребром а?
Воспользовавшись теоремой Пифагора, вычисляем диагональ куба, которая равна произведению ребра куба (а) на корень квадратный из трех.
Интересные материалы:
Как правильно должен падать свет на стол?
Как правильно дозвониться до вас или к вам?
Как правильно двадцать или двадцать?
Как правильно дышать через нос?
Как правильно есть фрукты по этикету?
Как правильно есть глину?
Как правильно есть крылышки по этикету?
Как правильно есть лангустов?
Как правильно есть мясо в супе?
Как правильно есть речную рыбу?
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
-
Формулы для куба
-
Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
-
Диагональ
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.

- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
![]()
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
![]()
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
![]()
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
![]()
Объем
Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
![]()
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
![]()
