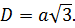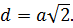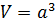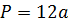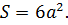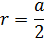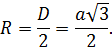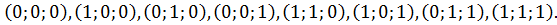Радиус описанной сферы куба
Свойства
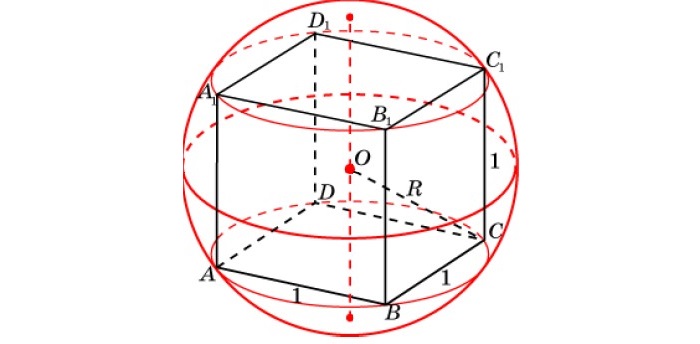
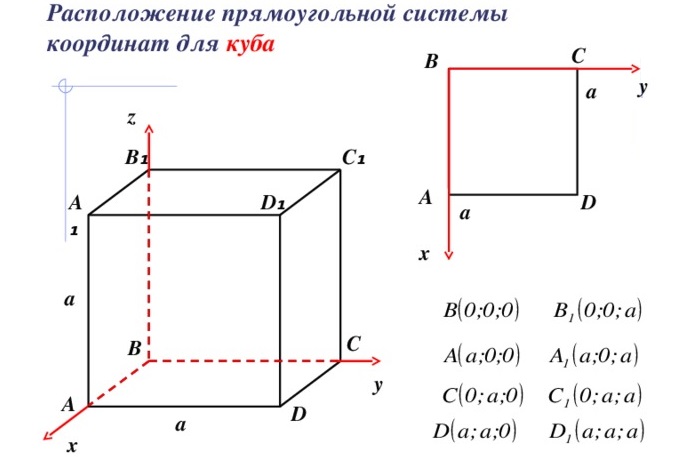
Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R
Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R
Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3
Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)
Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3
Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
[spoiler title=”источники:”]
http://matworld.ru/geometry/kvadrat.php
[/spoiler]
Содержание
- Куб — свойства, виды и формулы
- Элементы куба
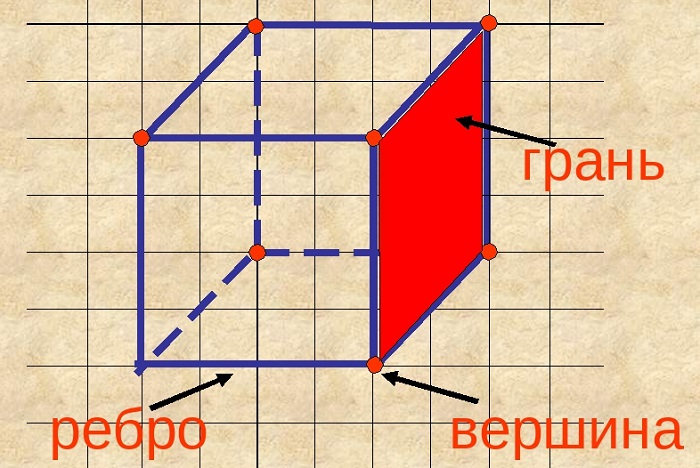
- Грань
- Ребро
- Вершина
- Центр грани
- Центр куба
- Ось куба
- Диагональ куба
- Диагональ грани куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершин куба
- Свойства куба
- Геометрические фигуры. Куб.
- Элементы куба
- Грань
- Ребро
- Вершина
- Центр грани
- Центр куба
- Ось куба
- Диагональ куба
- Диагональ грани куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершин куба
- Свойства куба
- Что такое куб: определение, свойства, формулы
- Определение куба
- Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
- Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
- Что такое сторона куба
- Свойства куба:
- Прямоугольный параллелепипед
- Пирамида
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
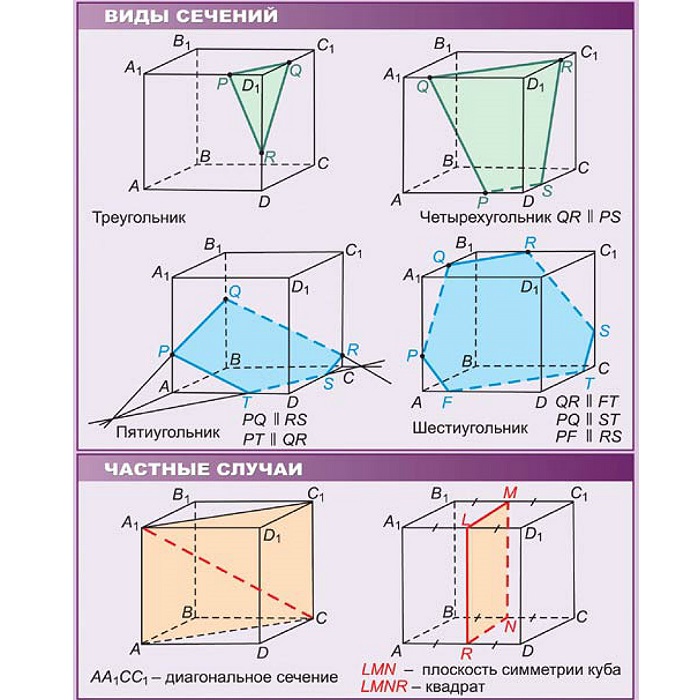
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Источник
Геометрические фигуры. Куб.
Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.
Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных
шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.
В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,
сумма плоских углов у каждой вершины = 270º.
Число сторон у грани – 4;
Общее число граней – 6;
Число рёбер примыкающих к вершине – 3;
Общее число вершин – 8;
Общее число рёбер – 12;

Предположим, что а – длина стороны куба, а d — диагональ, тогда:
Диагональ куба – это отрезок, который соединяет 2 вершины, которые симметричны относительно центра
Свойства куба.
перпендикулярно четырём его главным диагоналям.
совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба. В 1-м
случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной
из вершин куба. Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно
противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от
6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра
располагается на 6-ти гранях куба.
Элементы симметрии куба.
Ось симметрии куба может пролегать или сквозь середины ребер, которые
параллельны, не принадлежащих одной из граней, или сквозь точку
пересечения диагоналей противолежащих граней. Центром симметрии
куба будет точка пересечения диагоналей куба.

Сквозь центр симметрии куба проходят 9 осей симметрии.
Плоскостей симметрии у куба тоже 9, они пролегают или
через противолежащие ребра (таких плоскостей 6), или
через середины противолежащих ребер (таких 3).
Источник
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Источник
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
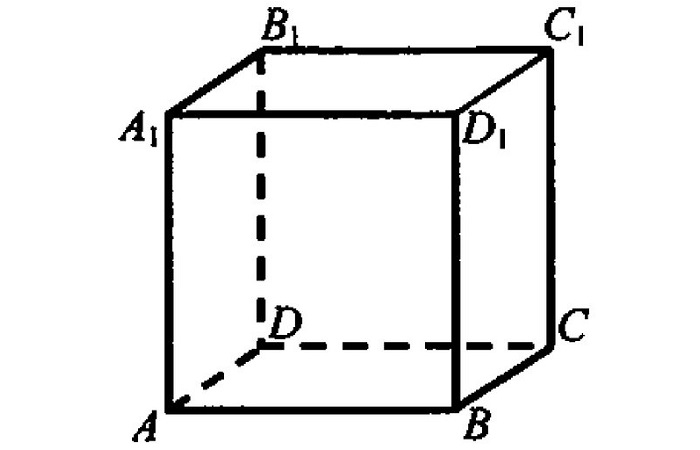
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Источник
Что такое сторона куба
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
Свойства куба:
2. Противоположные грани попарно параллельны.
3. Все двугранные углы куба – прямые.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$-высота(она же боковое ребро);
$S_<п.п>$-площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
Пирамида
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Формулы вычисления объема и площади поверхности правильной пирамиды.
В основании лежат правильные многоугольники, рассмотрим их площади:
Задачи на нахождение объема составного многогранника:
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Источник
Adblock
detector
Как найти сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней куба называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).
Вам понадобится
- калькулятор
Инструкция
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П – площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ – функция извлечения кубического корня).
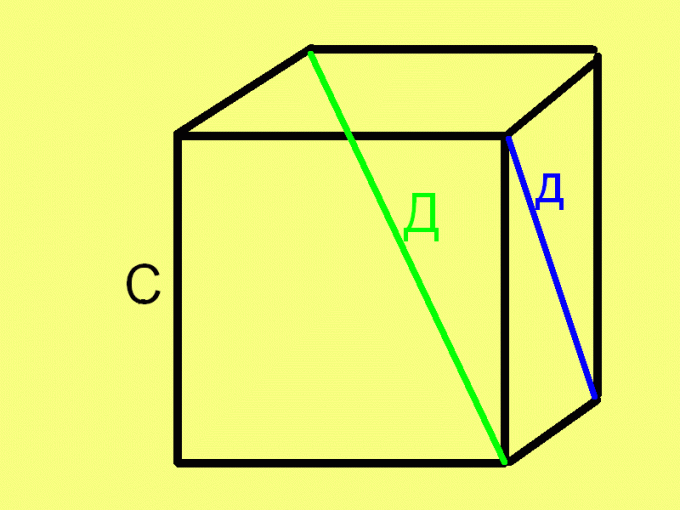
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Полезный совет
Для нахождения квадратных и кубических корней воспользуйтесь инженерным калькулятором. Чтобы извлечь корень третьей степени возведите число в степень ⅓.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Зная ребро куба, геометрический калькулятор может рассчитать все остальные его параметры, такие как объем, площадь, диагонали и радиус сфер, которые могут быть вписаны в куб или описаны вокруг него.
Площадь стороны куба, то есть его грани, является площадью квадрата со стороной а, являющейся одновременно ребром куба. Поэтому чтобы вычислить площадь стороны куба, нужно применить стандартную формулу площади квадрата.
S=a^2
Площадь боковой поверхности куба состоит из 4 боковых граней, а площадь полной поверхности – из 6 граней, поэтому их формулы представляют собой произведения площади одной грани куба на их необходимое количество.
S_(б.п.)=4a^2
S_(п.п.)=6a^2
Чтобы вычислить объем куба, зная его ребро, необходимо возвести его в третью степень, так как все три измерения куба – длина, ширина и высота, – равны между собой.
V=a^3
В некоторых случаях появляется необходимость рассчитать периметр куба, то есть сумму длин всех его ребер. В таком случае, периметр куба равен ребру куба, умноженному на 12.
P=12a
Диагональ грани куба d – это диагональ квадрата, для которой была выведена стандартная формула по теореме Пифагора.
d=a√2
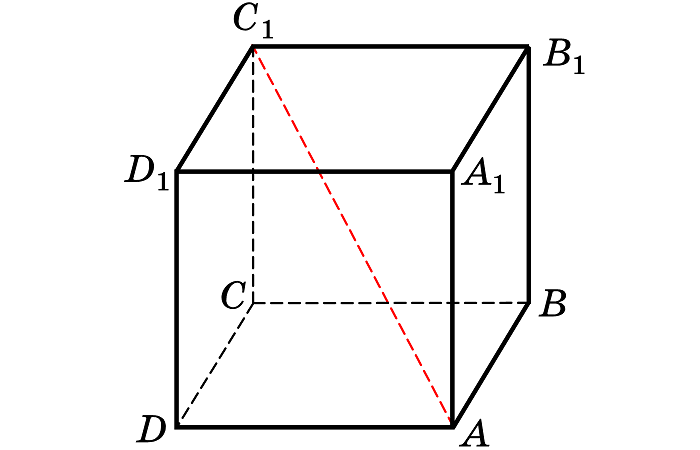
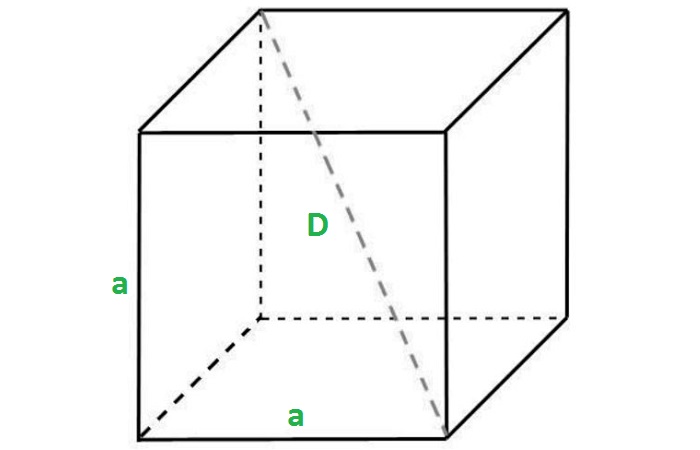
Диагональ куба D в свою очередь соединяет противоположные вершины верхнего и нижнего оснований, образуя с боковым ребром и диагональю основания прямоугольный треугольник. Теорема Пифагора в таком треугольнике приводит к единой формуле и для диагонали куба. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3
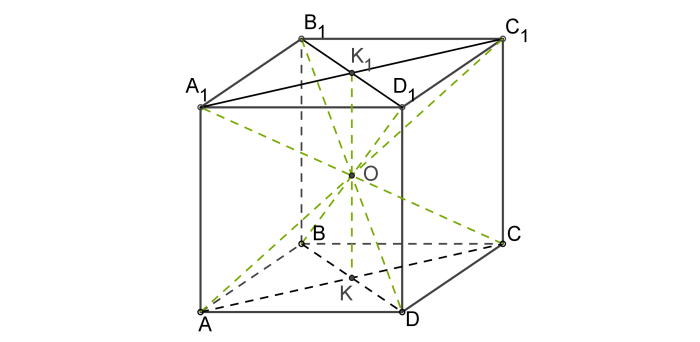
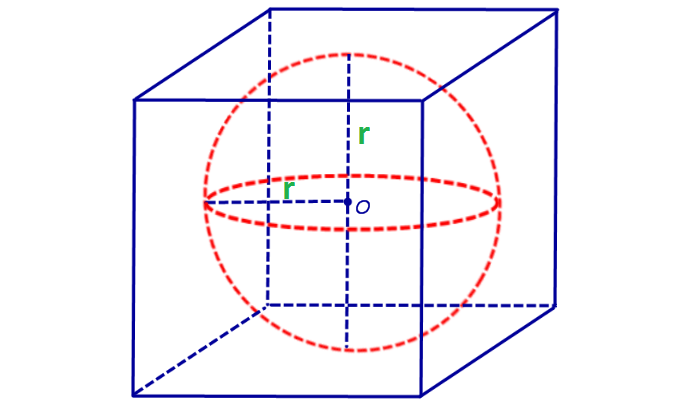
По аналогии с вписанной и описанной окружностью около квадрата, вписанная и описанная сферы около куба имеют схожие определения радиусов. Радиус вписанной сферы представляет собой половину ребра куба, а радиус описанной окружности – половину диагонали куба. (рис. 2.2, рис.2.3)
r=a/2
R=D/2=(a√3)/2
Содержание
- – Как вычислить объем куба?
- – Как определить грань куба?
- – Как найти объем куба если известна длина ребра?
- – Как называется сторона куба?
- – Как найти площадь поверхности куба?
- – Как вычислить объем прямоугольника?
- – Как найти Объëм?
- – Как посчитать м3 помещения?
- – Что такое грань определение?
- – Какие свойства имеет куб?
- – Как узнать объем цилиндра формула?
Как вычислить объем куба?
Куб – это геометрическая фигура, которая представляет собой правильный многогранник, где каждая его грань является квадратом. Объем куба можно вычислить, зная только значение длины его ребра. Так как все его ребра между собой равны. Говоря проще объем куба приравнивается кубу длины его ребра.
Как определить грань куба?
Грань куба – это часть плоскости, ограниченная сторонами квадрата. – куб имеет шесть граней; – каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани; – грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.
Как найти объем куба если известна длина ребра?
Все довольно просто. Объем = длина*ширина*высота. Ребро куба – это и есть его сторона, а все стороны в кубе равны. Следовательно, V= 1*1*1 = 1 кубический см.
Как называется сторона куба?
Куб – это многогранник, поверхность которого состоит из шести квадратов. Грани куба – это стороны куба, которые представляют собой квадрат. Ребра куба – это стороны граней куба. Вершина куба– это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.
Как найти площадь поверхности куба?
Куб – это один из пяти типов правильных многогранников, являющийся правильным прямоугольным параллелепипедом, имеет шесть граней, каждая из которых является квадратом. Площадь поверхности куба равна сумме площадей всех его шести граней.
Как вычислить объем прямоугольника?
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Как найти Объëм?
Объем параллелепипеда равен произведению площади основания на высоту.
…
V = a * b * h.
| a | длина параллелепипеда |
|---|---|
| h | высота параллелепипеда |
| P (осн) | периметр основания |
| S (осн) | площадь основания |
| S (бок) | площадь боковой поверхности |
Как посчитать м3 помещения?
К = Д х Ш х В, где: К – кубатура помещения (объем, выраженный в кубических метрах), Д, Ш и В – длина, ширина и высота помещения, выраженные в метрах, соответственно. Например, если длина помещения составляет 11 метров, ширина – 5 метров, а высота – 2 метра, то его кубатура будет 11 х 5 х 2 = 110 кубометров.
Что такое грань определение?
Грань — многозначный термин: Грань — плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Грань — часть цифр большого числа, выделенная из него каким-нибудь знаком. Грань числового множества — обобщение понятий максимума и минимума множества.
Какие свойства имеет куб?
Свойства куба:
- В кубе 6 граней и все они являются квадратами.
- Противоположные грани попарно параллельны.
- Все двугранные углы куба – прямые.
- Диагонали равны.
- Куб имеет 4 диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Диагональ куба в √ 3 раз больше его ребра
Как узнать объем цилиндра формула?
Формулы для вычисления объема цилиндра
$ V = pi r^2 h$ где: π – число пи (3.1415); h – высота цилиндра; r – радиус основания.
Интересные материалы:
Как заменить стандартный плеер на андроид?
Как запаривать пшеницу для бройлеров?
Как заправить узкий скотч в маленький диспенсер?
Как заправить зажигалку газом?
Как заправляется домкрат?
Как заправлять баллон со сливками?
Как запустить диспетчер печати через командную строку?
Как запустить Epson Status Monitor?
Как запустить каталитическую очистку духовки?
Как запустить квадрокоптер с пульта?