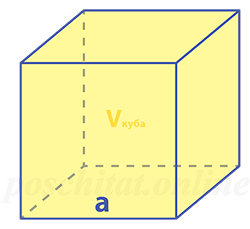
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
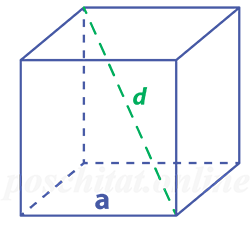
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
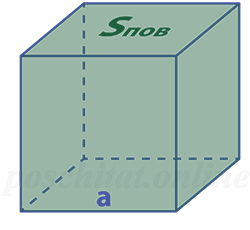
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также

как найти ребро куба, если известна диагональ
Светило науки – 9801 ответ – 46531 помощь
Примем ребро куба за а.
Диагональ d основания равна а√2.
Диагональ D куба – это гипотенуза треугольника, где катеты: диагональ d основания и ребро куба a.
D = √(d²+a²) = √(2a²+a²) = √(3a²) = a√3.
Отсюда получаем: а = D/√3.
Светило науки – 3 ответа – 0 раз оказано помощи
если сторона куба равна х,
диагональ стороны куба равна корень из 2х квадрат.
теперь вычислить диагональ куба – гипотенуза прямоугольного треугольника со сторонами х и уже вычисленной стороной
Лучший ответ
Альфия АBDEEVА
Знаток
(376)
13 лет назад
если сторона куба равна х,
диаглналь стороны куба равна корень из 2х квадрат.
теперь вычислить диагональ куба – гипотенуза прямоугольного треугольника со сторонами х и уже вычисленной стороной
Остальные ответы
Ольга Зиброва
Ученик
(112)
13 лет назад
через треугольники
Анастасия
Гуру
(4396)
13 лет назад
у куба все стороны равны? или нет? я уже не помню)) если равны, то диагональ :2
Светлана Светикова
Знаток
(369)
13 лет назад
ребро равно квадратный корень из квадрата диагонали деленного на 2
ed potter
Гуру
(3517)
13 лет назад
По теореме пифагора находите катеты, которые и являются ребрами.
Как найти сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней куба называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).
Вам понадобится
- калькулятор
Инструкция
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П – площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ – функция извлечения кубического корня).
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Полезный совет
Для нахождения квадратных и кубических корней воспользуйтесь инженерным калькулятором. Чтобы извлечь корень третьей степени возведите число в степень ⅓.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Куб является первым представителем в ряду правильных многогранников, благодаря тому, что все его ребра равны между собой. Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.
Также можно найти ребро куба, зная площадь основания:
Поскольку у куба могут быть даны площади боковой и полной его поверхности, приведем необходимые формулы ребра куба и для них:

Если исходить из понятия ребра, как части объемного тела, то в таком случае становится возможным вычислить ребро куба, зная его объем:
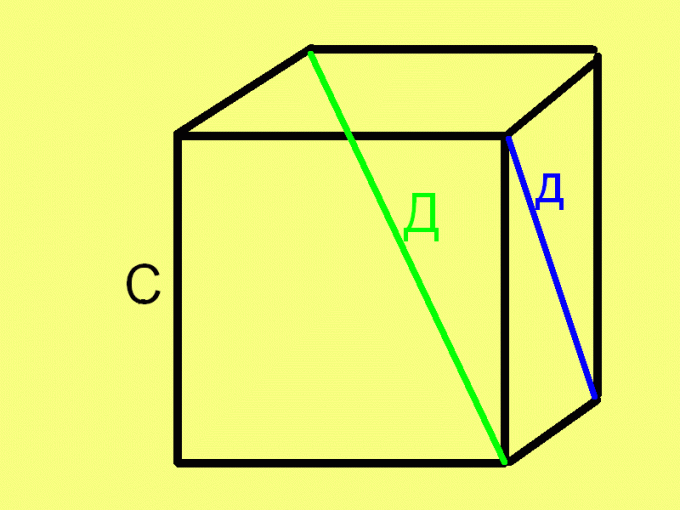
Одной из немаловажных деталей куба является его диагональ, соединяющая противоположные вершины верхнего и нижнего оснований, впрочем, для куба это могут быть любые два противоположных основания, так как все его грани конгруэнтны. Диагональ куба D, соединенная с диагональю основания d и ребром a дает прямоугольный треугольник, в котором из теоремы Пифагора можно найти ребро куба следующим образом.
a2+d2=D2
3a2=D2